质点沿竖直光滑曲线运动时脱离约束点研究

田宝国　吴世永　宿德志

(海军航空工程学院基础部　山东 烟台　264001)



质点沿竖直光滑曲线运动时脱离约束点研究

田宝国吴世永宿德志

(海军航空工程学院基础部山东 烟台264001)

利用质点运动动力学方程和机械能守恒定律，对质点在竖直平面内沿任意光滑曲线运动时脱离曲线的条件进行了研究，根据曲线方程的不同形式给出了质点脱离约束时的一般公式，并通过具体实例进行了验证．

光滑曲线脱离约束牛顿运动定律

在质点沿竖直平面内光滑曲线自由下滑过程中，如果在某处质点所受的支持力为零，则质点就会脱离曲线的约束而运动．在一些教材中，主要针对曲线为圆和抛物线的情况进行了讨论[1，2]．本文利用质点运动的动力学方程和机械能守恒定律以及各种曲线方程的曲率半径公式，推导出了质点在竖直平面内沿任意光滑曲线自由下滑时脱离曲线约束的一般结论，给出了在各种曲线方程形式下质点脱离曲线时的一般公式，并借此对圆、抛物线、正弦曲线等具体曲线的例子进行了研究．

1　质点脱离曲线的一般公式

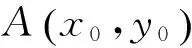
(1)

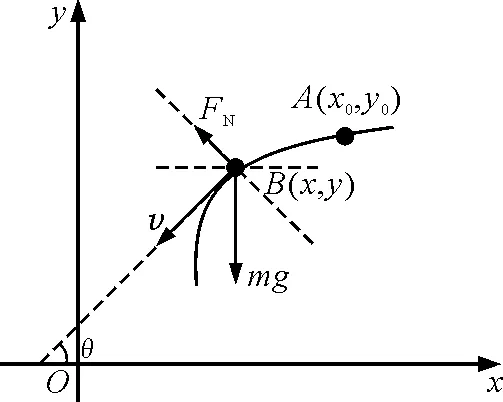
图1

其中，ρ为曲线在B点处的曲率半径．当质点脱离曲线约束时，FN=0，于是得

(2)

根据机械能守恒定律

(3)

由式(2)和式(3)得到

(4)

其中

(5)

下面根据不同曲线方程的形式给出质点脱离曲线约束时的一般表达式．

(1)若曲线方程为y=f(x)，则曲率半径表达式为[3]

(6)

当物体能够脱离约束，曲线必为凸曲线，即

y″<0，为保证曲率半径为正，则

(7)

由式(4)、(6)、(7)可得此时脱离曲线约束时满足的方程为

1+y′2=2(y-y0)y″

(8)

(9)

由式(4)、(6)、(9)可得此时脱离曲线约束时满足的方程为

(10)

即

(11)

(12)

(13)

式(8)、(11)和(13)即为在不同曲线方程形式下质点脱离曲线约束时满足的表达式．

2　应用举例

(1)曲线为半径为R的圆

图2

若质点的轨迹方程为

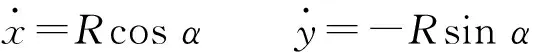
代入式(13)可得

3cosα=2

(2)椭圆

图3

质点的轨迹方程为

设质点从最高点y0=b处由静止下滑．由轨迹方程可得

代入式(11)可得方程

其根的判别式为

所以方程有一个实根和两个复根，实根表达式即为质点下滑时脱离曲线的位置，根据一元三次代数方程求根卡尔丹公式[3]可得质点脱离曲线约束时的解为

(3)抛物线

图4

质点轨迹方程为

设质点从原点O由静止开始下滑，由轨迹方程可得

y′=-2axy″=-2a

代入式(8)得到

2ax=0

因为x>0，所以方程无解，说明质点自由下滑过程中不会脱离该抛物线．

(4)正弦曲线

质点轨迹方程为

y=asinx

a2sin2x-2a2sinx+a2+1=0

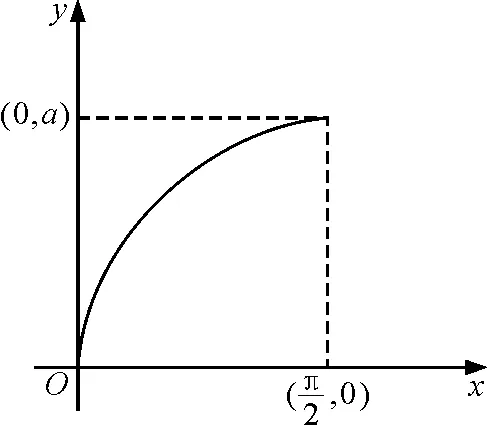
图5

根据本文结论，可对任意形状的平面曲线，如双曲正弦线、普通摆线等进行研究，在此不再赘述．

1李书民. 经典力学概论.合肥：中国科学技术大学出版社, 2007.13～14

2周衍柏. 理论力学教程. 北京： 高等教育出版社, 2010.

73～74

3数学手册编写组.数学手册.北京：高等教育出版社,2009.88,378

2015-03-23)