超临界流体中声空化泡的特性研究*

卢义刚　蔡苗

(华南理工大学 物理与光电学院，广东 广州 510640)



超临界流体中声空化泡的特性研究*

卢义刚蔡苗

(华南理工大学 物理与光电学院，广东 广州 510640)

根据物质的临界点物性参数,提出了在超临界流体中人为植入空化核的原则和方法.从超临界流体静压力高、表面张力小、空化泡内无蒸汽等物性特点出发,根据瑞利模型分析导出了超临界流体的空化阈值.考虑超临界流体具有很强的可压缩性,结合其物性特点,给出了能够用于超临界流体空化计算分析的简化Gilmore方程.根据美国国家标准局提供的超临界二氧化碳流体的物性数据,拟合出密度-压力关系式及声速-压力关系式,并用于Gilmore方程的计算.计算分析了超临界二氧化碳流体中空化泡的初始半径、流体温度、声压幅值、声波频率等因素对空化过程的影响.研究表明：超临界流体的空化阈值与其静压力相当；超声波声压幅值超过超临界流体的空化阈值后,气泡在超声波作用下的运动特征与在水等常规液体中的空化泡运动特征相同.

超声空化；空化气泡；空化阈值；声压幅值；超临界流体；Gilmore方程

瑞利解释了液体的空化机理[1].之后，众多学者对瑞利方程进行了修正，有考虑了液体表面张力和粘性的R-P方程[2]、考虑了含气量影响的Nolting-Neppiras方程[3]、考虑了热传导因素的Yasui方程[4]，还有考虑了液体可压缩性的Gilmore方程[5].液体空化时在局部空间产生高温和高压等效应，使得空化技术得到了广泛应用.截至目前，关于声空化理论和应用技术的研究都取得了较为丰富的成果.但是，这些研究都是在水和一些常规液体中进行的.直到2002年，Kuijpers等才在高压液态二氧化碳中利用超声波诱发出空化[6].

当温度和压强均超过临界点时，物体便处于超临界态，成为超临界流体.超临界流体具有特殊的物性，在许多领域得到应用，形成了独具特色的超临界流体技术[7-8].为了提高超临界流体技术的效率，科学工作者开始研究强化超临界流体技术的各种手段，其中，超声波强化取得了显著的效果[9].但至今仍未有实验确切证实超临界流体中能够产生空化，也没有理论明确回答能否在超临界流体中产生空化的问题.文中将在分析形成空化核的方法和估算超临界流体声空化阈值的基础上，考虑超临界流体的可压缩性，应用Gilmore方程计算分析超临界流体中空化泡的运动特性.

1　超临界流体的空化阈值

迄今为止，学术界普遍认为，在超临界流体中由于没有相边界，空化难以发生[6].类似于水等常规液体，当超临界流体中存在结构薄弱区域即空化核时，空化容易发生.为此，可先向超临界流体物质中加入临界点较高的其他气体，在超临界流体物质处于超临界态时，所加入的气体介质仍处于气态.如在CO2中注入少量氨，氨的临界温度为133 ℃、临界压力为11.3 MPa，CO2的临界温度为31.2 ℃、临界压力为7.38 MPa，这样就在超临界CO2中人为地植入了空化核.在实际情况中，并不能保证超临界流体物质的纯净，这些杂质也可以形成空化核.

根据现有空化理论，在液体中，为了激发空化核生长，所需要的最小声压-阈值声压为

(1)

式中，PB为阈值声压，P0为液体的环境压强，Pv为液体的饱和蒸汽压，σ为液体的表面张力，R0为气泡的初始半径.

超临界流体的表面张力很小，即使气泡的初始半径很小，如取R0=10-5m时，对应的拉普拉斯压强2σ/R0≈0.66 kPa，也远小于超临界流体的静压强[6].因此，表面张力对超临界流体空化阈值的贡献可以忽略.此外，超临界流体为单一相态，饱和蒸汽压Pv=0.由式(1)可知PB≈P0，这表明，超临界流体的空化阈值与其静压强相当.

2　超临界流体的Gilmore方程

相比于水等常规液体，超临界流体具有很大的可压缩性.特别是在临界点附近，压力和温度的微小变化就会引起超临界流体的密度发生很大的变化[10].因此，在研究超临界流体的空化问题时，必须考虑其可压缩性带来的影响.Gilmore方程在推导过程中引用了柯克伍德-贝蒂假设：压强扰动传播的速度等于音速和液体局部速度之和，从而考虑了流体的可压缩性对气泡运动过程的影响，适用于需要考虑可压缩性影响的超临界CO2流体，其方程如下：

(2)

(3)

式中：ρ是超临界流体的密度，P(R)为泡壁处的压强.

根据瑞利理论，流体中的气泡，除受到超声波的作用外，还受其他多个力的作用，泡壁处的压强可以表示为

(4)

其中：Pg为泡内气体压强；μ为超临界流体的粘滞系数；PA和ω分别为超声波的声压振幅和频率.

视泡内气体为理想气体，在球型空化泡模型下，泡内气体压强可表达为

(5)

式中，Pg0为泡内气体初始压强，γ为气体的多变指数.

考虑到Pv=0及σ=0，并假定泡内气体作绝热变化(在后面的数值计算中取γ=1.33)，则式(4)简化为

(6)

要求解Gilmore方程(式(2))，需要得到焓的表达式，即掌握流体的密度-压力关系.为此，有学者利用Tait经验关系式来描述流体的密度-压力关系[11-12]，但Tait经验关系式是根据水的物性数据拟合而来，不适合超临界流体.为了描述超临CO2的密度-压力关系，文献[13]在文献[14]的基础上，结合超临CO2的物性参数，从Tait经验关系式出发，推导得到了适用于计算分析超临CO2中空化泡运动状态的物态方程.该方程代入到超临CO2流体中虽然具有一定的适用性，但其适用范围较窄，仅对部分温度和压力适用.至今为止，仍没有一个状态方程能够简单且准确地描述超临CO2流体的密度-压力关系.但美国国家标准局(NIST)提供了大量超临CO2的物性数据，文中根据NIST提供的数值，采用多项式拟合，得到在某一温度下的的超临CO2压力-密度关系.利用该多项式拟合得到的压力-密度关系式不仅准确，而且形式简单，代入Gilmore方程计算时非常方便，拟合方程形式如下：

(7)

式中，ai为拟合高阶多项式第i次项的系数.

将式(7)代入式(3)得到焓的表达式：

(8)

即

(9)

结合式(6)得到：

(10)

将式(10)两边对t求导，得到：

(11)

再将式(10)-(11)代入式(2)，得到能用于超临界流体声空化计算分析的Gilmore方程，方程形式如下：

(12)

根据NIST提供的超临界CO2的物性参数，拟合出超临界CO2的压力-密度关系式，并结合超临界CO2表面张力小、粘滞系数小的特性，将其代入Gilmore方程得到式(12).超临界流体的可压缩性不仅表现为密度波动，还表现为声速波动.超临界CO2在临界点附近声速会产生巨大的变化，在利用Gilmore方程分析超临界CO2中空化泡的运动状态时，不能忽略声速变化所带来的影响.文中利用NIST提供的超临界CO2的声速和压力数据，类似于密度拟合，得到在某一定温度下声速与压力的关系，代入方程计算.声速表达式如下：

(13)

式中：bj为拟合高阶多项式第j次项的系数.

3　超临界CO2声空化泡运动特性

利用NIST提供的超临界CO2物性数据，可求解出系数ai和bj，进而得到密度-压力关系和声速-压力关系，再将密度-压力关系和声速-压力关系代入Gilmore方程(式(12))，利用Matlab编程进行数值计算分析，得到气泡半径随时间的变化关系，进而研究空化泡的动力学行为.

以气泡半径与初始半径比值Rt/R0为纵坐标，时间t为横坐标，在超声频率为20kHz，声压幅值为10MPa条件下，假定超临界CO2温度为310K，R0分别取为5、10、15μm，得到空化泡运动与R0关系曲线，如图1所示.在超声波频率为20kHz，声压幅值为10MPa条件下，假定R0半径为10μm，流体温度分别取为310、 400、500K，得到空化泡运动与流体温度关系曲线，如图2所示.

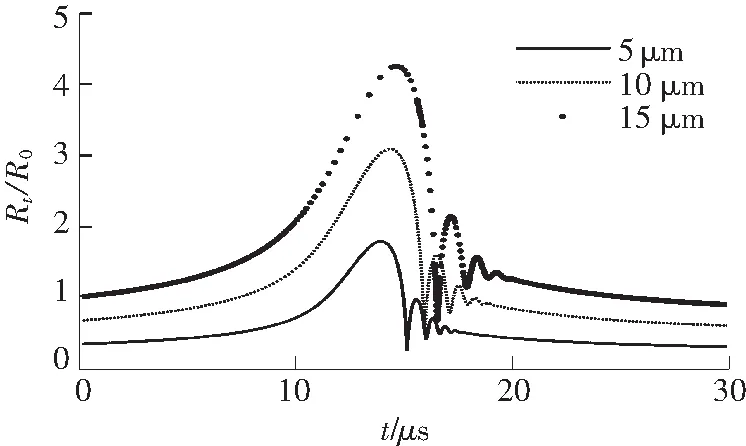
图1　初始半径对空化过程的影响

图2　流体温度对空化过程的影响

由图1可见，R0越大，Rt/R0越大，即运动幅度越大，空化程度相对激烈.R0增加，则气泡达到峰值半径所需的时间略有增大，且第一溃灭时间也随半径增大而推迟，即初始半径小的空化泡较早溃灭. 由图2可见，流体温度升高，空化泡膨胀所能达到的峰值半径增加，且出现峰值半径的时间有所提前.不同温度下泡的溃灭程度及过程基本一致，在接近临界温度时差异变大.

在超临界CO2流体温度为310K，R0为10μm条件下，假定超声超频率为20kHz，声压幅值分别取为9.8、9.9、10.0MPa,计算得到空化泡运动与声压幅值关系，如图3所示.在超临界CO2流体温度为310K，R0为10μm条件下，假定声压幅值为10MPa，超声频率分别取为20、30、40kHz，计算得到空化泡运动与超声频率关系如图4所示.

图3　声压幅值对空化过程的影响

Fig.3Effectofultrasonicamplitudeoncavitationprocess

图4　超声频率对空化过程的影响

由图3及图4可见，在一定的超声频率下，增大声压幅值，空化泡第一次膨胀时的峰值半径增大.随声压幅值的增大，泡达到峰值半径的时间滞后，泡的溃灭半径变小，泡的运动幅度加大，空化强度增大.声压幅值较大时，超临界流体的空化容易发生.声压幅值一定时，泡半径达到峰值及泡溃灭的时刻主要由超声频率决定，超声频率对空化泡的崩溃程度有一定的影响，低频时超临界流体的空化程度相对较强.

4　结论

[1]RAYLEIGHL.Onthepressuredevelopedinaliquiddu-ringthecollapseofasphericalcavity[J].PhilosophicalMagazine，1917，34 (3)：94-98.

[2]PLESSET M S.The dynamics of cavitation bubbles [J].Journal of Applied Mechanics，1949，16 (9)：277-282.

[3]NOLTINGK B K，NEPPIRAS E A.Cavitation produced by ultrasonics [J].Pmc Phys Soc London B，1950，63 (9)：674-685.

[4]YASUI K.Effects thermal conduction on bubble dynamic near the somolumince threshold [J].J Acoust Soc Am，1995，98 (5)：2772-2782.

[5]GILMORE F R.The growth and collapse of a spherical bubble in a viscous compressible liquid [R].California： Hydro Lab Calif lnst Tech Report，1952.

[6]KUIJPERS M W A，VAN ECK D，KEMMERE M F，et al.Cavitation-induced reaction in high-pressure carbon dioxi-de [J].Science，2002，298 (5600)：1969-1971.

[7]ENOKIDA Y，EL-FATAH S A，WAI C M.Ultrasoun denhanced dissolution of UO2in supercritical CO2containing a CO2-philic complexant of tri-n butylphosphate and nitric acid [J].Industrial & Engineering Chemistry Research，2002，41(9)： 2282-2286.

[8]TROFIMOV T I，SAMSONOV M D，LEE S C，et al.Ultrasound enhancement of dissolution kinetics of uranium oxi-des in supercritical carbon dioxide [J].Journal of Chemical Technology and Biotechnology，2001，76 (12)：1223-1226.

[9]BALACHANDRAN S，KENTISH S E，MAWSON R，et al.Ultrasonic enhancement of the supercritical extraction from ginger [J].Ultrasonic Sonochemistry，2006，13 (6)： 471-479.

[10]罗奔毅，卢义刚.超临界点附近二氧化碳流体的声速 [J].物理学报，2008，57 (7)： 4397-4401.

LUO Ben-yi，LU Yi-gang.Study of sound speed in near-critical carbon dioxide [J].Acta Physica Sinica，2008，57(7)：4397-4401.

[11]YUAN L，CHENG H Y，CHU M C，et al.Physical parameters affecting sonolumine-scence： A self-consistent hydrody-namic study [J].Physical Review E，1998，57 (4)：4265-4280.

[12]COLE R H.Underwater explosions [M].New York： Princeton University Press，1948：38-45.

[13]CHEN G，LU Y.Cavitation in compressible supercritical carbon dioxide [J].Physics and Chemistry of Liquids，2015，53(1)：67-74.

[14]李志旺，严家騄.一个新的液体状态方程 [J].工程热物理学报，1990，11 (2)：126-128.

LI Zhi-wang，YAN Jia-lu.A new equation of state for li-quid [J].Journal of Engineering Thermophysics，1990，11(2)：126-128.

s： Supported by the National Natural Science Foundation of China (11174086,11574089)

A Probe into Characteristics of Acoustic Cavitation Bubbles in Supercritical Fluid

LUYi-GangCAIMiao

(School of Physics and Optoelectronics，South China University of Technology，Guangzhou 510640，Guangdong，China)

Firstly，according to the physical parameters of substance’s critical point，the principles and methods for artificial implantation of cavitation nuclei in supercritical fluid are proposed. Secondly，by analyzing the physical characteristics of supercritical fluid，such as high hydrostatic pressure，low surface tension and no steam inside cavi-tation bubbles，the cavitation threshold of supercritical fluid is derived with the help of Rayleigh model. Then，by comprehensively taking into consideration the strong compressibility and physical characteristics of supercritical fluid，a simplified Gilmore equation for the calculation and analysis of supercritical fluid cavitation is given. More-over，according to the experimental data provided by the American National Standards Institute，density-pressure relationship and sound speed-pressure relationship of supercritical CO2fluid are fitted to solve the Gilmore equation. Finally，the effects of initial radius，fluid temperature，sound pressure amplitude and ultrasonic frequency on the ultrasonic cavitation process are analyzed. The results indicate that the threshold of supercritical fluid is similar to hydrostatic pressure； and that，when ultrasonic sound pressure is greater than cavitation threshold，the movement of bubbles under the action of ultrasonic is similar to that of conventional liquids，such as water.

ultrasonic cavitation； cavitation bubble； cavitation threshold； sound pressure amplitude； supercritical fluid； Gilmore equation

1000-565X(2016)07-0142-05

2015-12-13

国家自然科学基金资助项目(11174086,11574089)

卢义刚(1962-)，男，博士，教授，主要从事超声技术研究.E-mail：phyiglu@scut.edu.cn

O 426.4doi： 10.3969/j.issn.1000-565X.2016.07.022