预制板式无砟轨道界面脱层失效的数值模拟*

戴公连　粟淼

(1.中南大学 土木工程学院，湖南 长沙，410075； 2.高速铁路建造技术国家工程实验室，湖南 长沙，410075)



预制板式无砟轨道界面脱层失效的数值模拟*

戴公连1,2粟淼1†

(1.中南大学 土木工程学院，湖南 长沙，410075； 2.高速铁路建造技术国家工程实验室，湖南 长沙，410075)

将温度荷载简化为轨道板内的剪切荷载，分析了无砟轨道结构的层间界面破坏形式与粘结机理；基于黏聚力本构模型与水泥乳化沥青砂浆界面粘结力实验结果，建立预制板式无砟轨道结构界面有限元模型，研究剪切荷载作用下无砟轨道界面应力、界面粘结承载力、界面相对位移以及界面裂缝的演化规律.结果表明：界面剪应力与正应力纵向分布不均匀，在轨道板端部最大，且界面正应力使轨道板在端部竖向受拉；剪切荷载作用下，界面剪应力超过最大粘结强度，造成界面逐段破坏，界面最大粘结承载力为264.8 kN；轨道板相对于砂浆充填层的纵向位移随剪切荷载的增大而持续增大，最终界面出现纵向裂缝，而其竖向张开位移在界面纵向裂缝出现后反而逐渐闭合，界面发生剪切破坏导致无砟轨道结构脱层失效.

无砟轨道；剪切荷载；界面；裂缝；失效；有限元模型；粘结强度；相对位移

温度荷载作用下，无砟轨道结构层之间存在剪力差，使得砂浆层与轨道板和支承基础层界面之间容易出现裂缝，裂缝张开宽度一般在1 mm以下，其延伸范围不等，最长可达十几米[3].界面裂缝会导致预制轨道板、砂浆充填层和支承层脱层，严重削弱轨道结构整体稳定性，影响轨道平顺性和列车运行安全性.但目前关于无砟轨道结构损伤特性的研究大多关注轨道板、支承层或道床板等结构层自身的裂缝、刚度退化等[4-7]，忽略了结构层间界面的开裂失效问题.结构层间界面开裂失效将导致预制轨道板的约束条件较初始设计时发生改变，轨道结构在温度荷载等作用下发生翘曲变形、滑移等，给结构安全性带来不利影响.

文中阐述了剪切荷载作用下预制板式无砟轨道结构界面的破坏形式及粘结机理，采用黏聚力本构模型描述轨道板与砂浆层的界面力学行为，建立无砟轨道结构界面数值模型，将温度荷载简化为轨道板内剪切荷载，研究其作用下界面裂缝的形成及发展过程.

1　剪切荷载作用下无砟轨道界面粘结机理

剪切荷载作用下，预制板式无砟轨道结构层界面主要有两种破坏形式：砂浆充填层与预制轨道板和支承基础层之间均产生裂缝(见图1(a))；裂缝仅发生在轨道板与砂浆层界面(见图1(b)).实际工程中，由于受施工方法影响，界面2的粘结强度往往要远大于界面1的粘结强度，使得板式无砟轨道结构的界面损伤以第二种破坏形式为主，文中主要研究该种界面开裂形式下的破坏机理.

(a)界面1和界面2同时开裂

(b)界面1开裂

为分析砂浆层与轨道板界面的粘结机理，取一段长度为L的轨道板和砂浆层，在轨道板两端作用有剪切荷载p0，分析其单元受力情况.由于砂浆充填层与支承基础层之间的粘结力足够大，剪切荷载作用下该层界面(界面2)基本没有相对位移，可将结构进一步简化，认为砂浆充填层下表面完全固定，作为结构的边界条件，如图2所示.

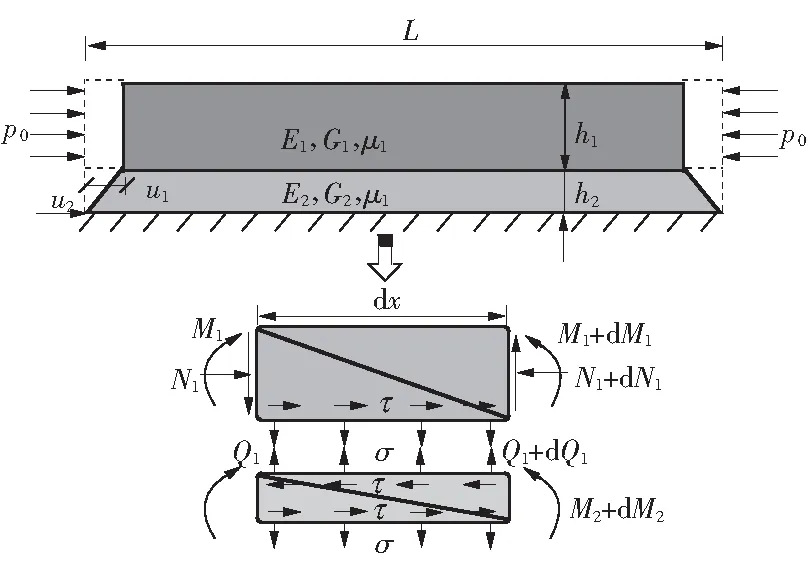
图2　界面粘结机理分析

图2中，N1、Q1、M1分别为轨道板轴力、剪力和弯矩；M2为砂浆充填层弯矩；σ、分别为界面正应力和界面剪应力.对轨道板进行受力分析，可知：

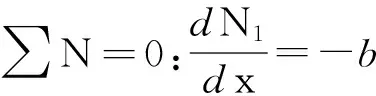
(1)

(2)

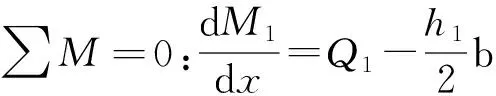
(3)

对砂浆层进行受力分析，可知：

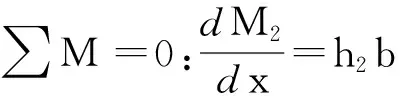
(4)

式中，h1、h2分别为轨道板与砂浆结构层的厚度，b为轨道板宽度.

可见，剪切荷载作用下轨道板与砂浆层界面存在一定的剪应力和正应力，且剪应力为主要应力[8].若界面始终处于弹性工作状态，根据文献[9]，假设界面剪应力正比于砂浆层的剪切模量和剪切变形，则界面剪应力可表示为

(5)

其中：G2为砂浆层剪切模量；u1、u2分别为轨道板底缘与砂浆层顶缘的纵向位移，若不考虑结构层中弯矩和正应力的影响，则有du1/dx=N1/E1A1，du2/dx=0，其中E1、A1分别为轨道板的弹性模量和截面面积.

对式(5)求导并将式(1)代入可得轨道板内轴力控制方程为

(6)

解得：

N1=c1eλx+c2e-λx

(7)

则可知剪应力为

(8)

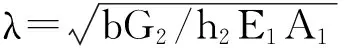
考虑边界条件为轨道板轴力N1在轨道板两端为p，可解得：

(9)

(10)

由式(8)可知，在x=0和x=L处(即板端)，剪应力最大，最大剪应力max=-λ/b(c1-c2).故在轨道板端附近容易出现结构层开裂、脱层现象，而考虑板内弯矩影响的界面应力以及界面进入弹塑形阶段后的力学行为还需通过数值模拟进一步分析.

2　数值仿真模型

2.1界面粘结力本构模型

实际中轨道板与砂浆层界面的粘结力与相对位移存在一种非线性关系，当界面应力达到界面粘结强度时，界面会出现裂纹萌生和扩展，发生脱层开裂破坏.采用黏聚力本构模型逐段线性张力位移法则描述无砟轨道结构中轨道板与砂浆层的界面性质[10-11]，见图3.国内外研究表明，黏聚力模型能比较接近真实情况地描述界面行为[12-13].

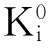
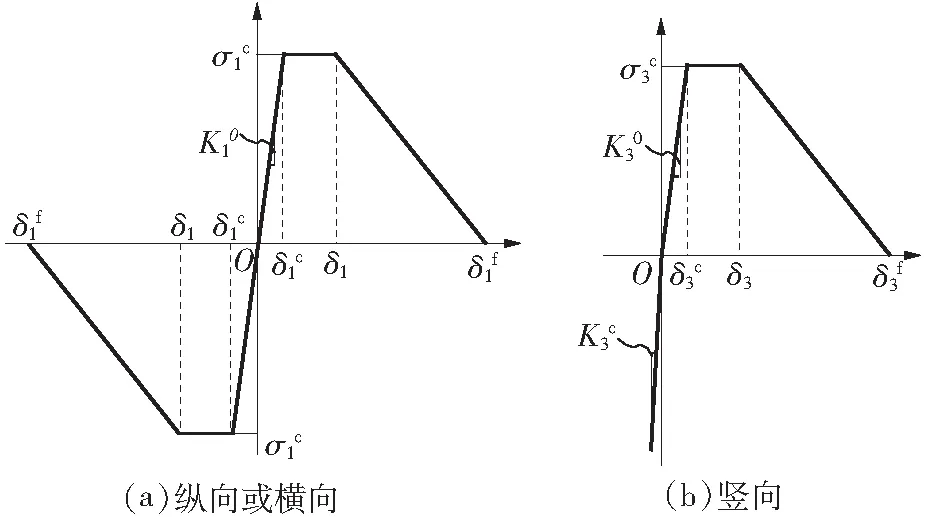
图3　无砟轨道界面粘结力本构模型

(11)

2.2有限元分析模型

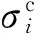
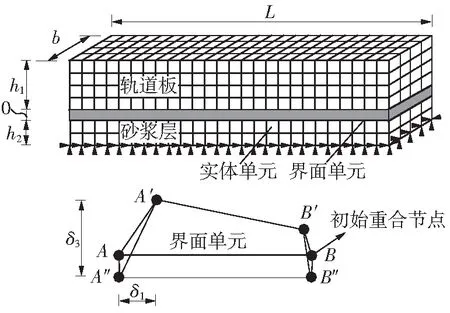
图4　无砟轨道界面有限元模型

3　计算结果及分析

3.1界面应力分析

图5给出了随着作用在轨道板两端的外荷载F的增大，轨道板与砂浆层界面纵向剪应力沿轨道板长度方向的变化情况.图中纵、横坐标分别为界面剪应力与最大剪应力的比值以及距板左端距离x与板长L的比值.其中，最大剪应力max=0.024 9MPa，即为模型中定义的界面纵向粘结强度，轨道板长度L为6.4m.当界面剪应力小于最大粘结强度时，界面处于弹性工作状态，其应力分布呈现在轨道板两端最大、向内部递减的趋势，沿板中心线对称，见图5(a).而在0.5L处由于轨道板与砂浆层始终没有相对运动的趋势，界面剪应力始终为零.从图中可以看出，在弹性阶段界面剪应力随着外荷载的增大而增大，但分布趋势保持不变，其在板端位置处最先达到最大粘结强度.

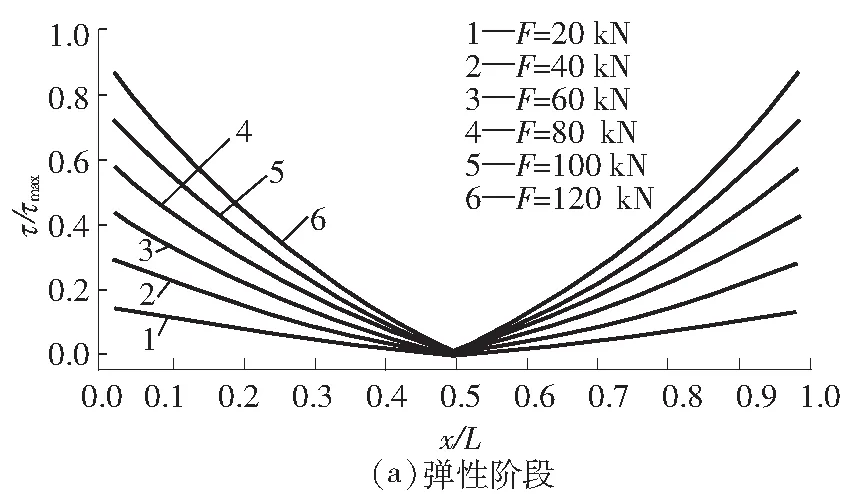
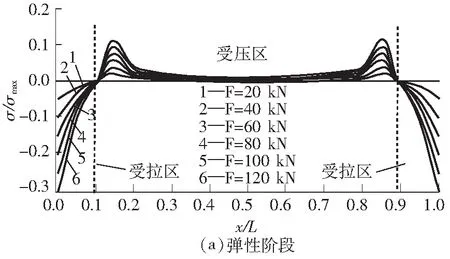
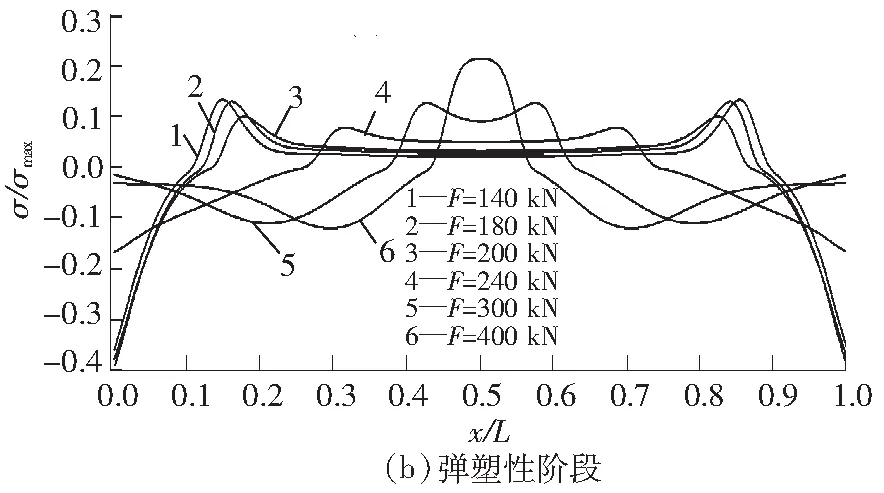
图6　界面正应力演化过程

3.2界面纵向粘结承载力

由于外荷载、无砟轨道结构以及界面应力均关于轨道板中心对称，取一半结构分析，其界面粘结承载力定义为

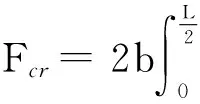
(12)

从式(12)可知，Fcr即为图5中剪应力分布曲线与横坐标轴所形成的面积再乘以轨道板宽度b.图7所示为距轨道板板端不同位置处的界面粘结承载力-界面相对纵向位移(Δ)曲线.

图7　界面纵向粘结承载力-位移曲线

在文中所取的界面粘结强度和界面刚度参数条件下，计算得到的界面最大纵向粘结承载力为264.8 kN，达到粘结承载力时板端、距板端L/8、L/4、3L/8的界面相对纵向位移分别为0.021、0.013、0.007、0.003 mm.

3.3界面位移分布

不同外荷载F作用下，界面相对位移δi=Δs，i-Δc，i(Δs，i、Δc，i分别表示轨道板与砂浆层绝对位移，i表示方向)的变化趋势见图8和图9.

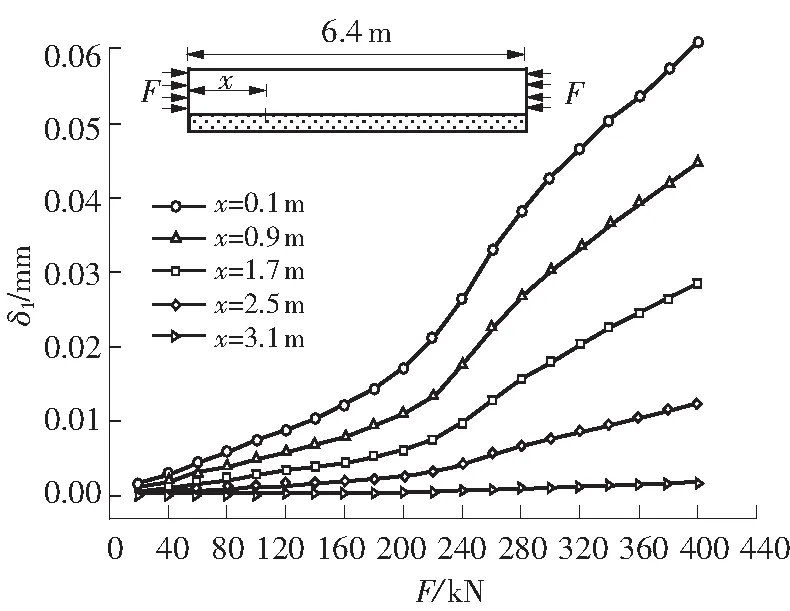
图8　界面相对纵向位移

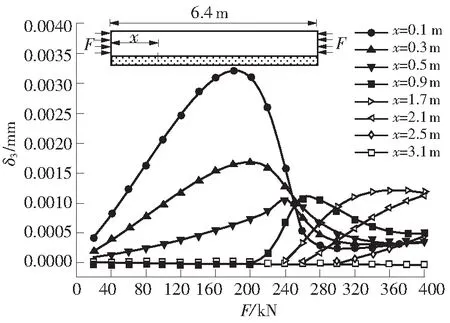
图9　界面相对竖向位移

由图8可见，界面相对纵向位移δ1随荷载F的增大不断增大；外荷载相同的条件下，越靠近加载端，其界面纵向位移越大.当F小于200 kN时，δ1与F基本呈线性关系；之后相对纵向位移的增长速率明显加快，说明界面此时开始进入弹塑性阶段.

从图9可以看出，界面相对竖向位移随荷载增大到一定数值后会迅速下降至零，这是由于当荷载F增大到一定数值后，界面开始出现纵向裂缝，导致整个界面完全开裂，该位置处不再能承载任何方向荷载，界面粘结力完全丧失，正应力降为零，故界面相对竖向位移δ3也迅速减为零.而随着外荷载的继续增大，裂纹逐渐向内发展.当F=250 kN时，距加载端0.3 m范围内界面的相对竖向位移基本下降为零，而此时距加载端0.9 m处的界面相对竖向位移恰好达到其最大值，但轨道板板端的最大竖向位移值要明显大于其内部.

3.4裂缝发展规律

在剪切荷载作用下，轨道板与砂浆层界面同时出现纵向和竖向相对位移，纵向相对位移随着荷载的增大而增大，且当荷载F达到一定数值后界面出现裂缝，而后随剪切荷载的增加纵向裂缝继续增大；而竖向相对位移在纵向裂缝出现后，由于界面丧失粘结力，界面不再存在正应力，使得竖向相对位移下降为零.根据文中数值模型，计算得到的界面裂缝矢量云图如图10所示.需说明的是，图10(a)、10(b) 中的裂缝实际上为假裂缝，若此时卸载其裂缝可以闭合，界面仍然处于弹性工作状态；而图10(c)、10(d) 中界面已经完全开裂，轨道板与砂浆层在板端附近已经分层失效.

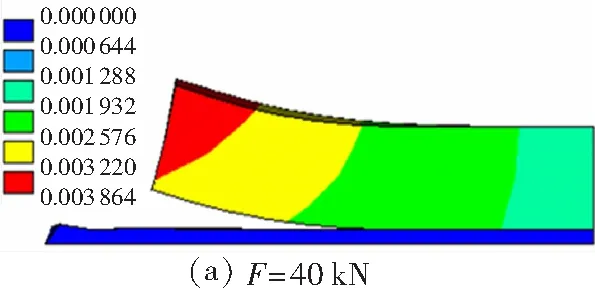
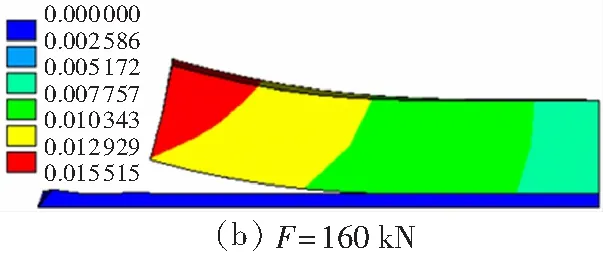
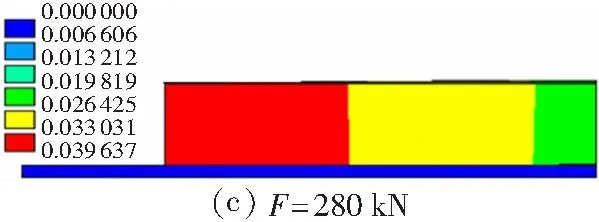
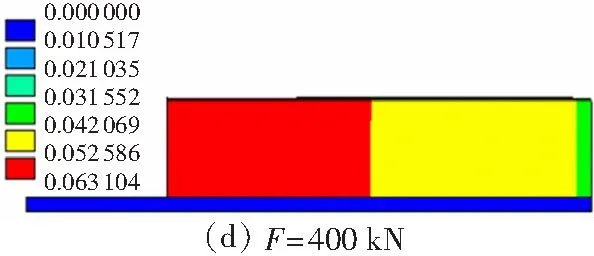
图10　界面裂缝发展过程(单位：mm)

4　结论

文中分析了剪切荷载作用下板式无砟轨道界面粘结机理，在忽略板中弯矩条件下推导了弹性阶段剪切荷载作用下预制无砟轨道结构界面剪应力理论公式；基于黏聚力本构模型和试验结果粘结力参数，建立了无砟轨道界面有限元模型.通过研究，得出以下主要结论：

(1)最大界面剪应力出现在轨道板板端.

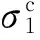
(3)剪切荷载作用下，轨道板与砂浆层存在纵向滑移与竖向张开的趋势，而一旦出现纵向裂缝，界面竖向相对位移闭合，界面发生剪切破坏.

(4)无砟轨道界面工作性能受界面粘结力参数影响很大，关于结构层不同材料之间的粘结力参数以及反复荷载作用下粘结力参数还需加强实验研究.

[1]田利民.客运专线无砟轨道系统设计 [J].中国铁道科学，2008，29(1)：13-16.

TIAN Li-min.Systematic design of ballastless track on passenger dedicated lines [J].China Railway Science，2008，29(1)：13-16.

[2]全顺喜，王平，陈嵘.无砟轨道高低和方向不平顺计算方法研究 [J].铁道学报，2012，34(5)：81-85.

QUAN Shun-xi，WANG Ping，CHEN Rong.Study on calculation methods of lateral and vertical profile irregularity of ballastless track [J].Journal of the China Railway Society，2012，34(5)：81-85.

[3]卢炜.严寒地区CRTS I型无砟轨道板四角离缝成因研究 [J].铁道工程学报，2014，31(7)：53-56，88.

LU Wei.Research on the seams genesis of CRTS-I ballastless track slab’s four corners in severe cold area [J].Journal of Railway Engineering Society，2014，31(7)：53-56，88.

[4]刘钰，陈攀，赵国堂.CRTSⅡ型板式无砟轨道结构早期温度场特征研究 [J].中国铁道科学，2014，35(1)：1-6.

LIU Yu，CHEN Pan，ZHAO Guo-tang.Study on the cha-racteristics of early temperature field of CRTS II slab ballastless track structure [J].China Railway Science，2014，35(1)：1-6.

[5]徐光鑫，杨荣山.双块式无砟轨道裂纹对道床板受力的影响分析 [J].铁道标准设计，2013，57(12)：50-53.

XU Guang-xin，YANG Rong-shan.Analysis of stress state of track slab under the influence of structure cracking of bi-block ballastless track [J].Railway Standard Design，2013，57(12)：50-53.

[6]何川.CRTS II型板式无砟轨道砂浆离缝的影响及维修指标研究 [D].成都：西南交通大学土木工程学院，2013.

[7]徐庆元，孟亚军，李斌，等.温度梯度作用下纵连板式无砟轨道疲劳应力谱 [J].中南大学学报(自然科学版)，2015，46(2)：736-741.

XU Qing-yuan，MENG Ya-jun，LI Bin，et al.Fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient [J].Journal of Central South University (Science and Technology)，2015，46(2)：736-741.

[8]NEEDLEMAN A.An analysis of intersonic crack growth under shear loading [J].Journal of Applied Mechanics-Transactions of the ASME，1999，66(4)：847-857.

[9]邓军，黄培彦.预应力CFRP板加固梁的界面应力分析 [J].工程力学，2009，26(7)：78-82，88.

DENG Jun，HUANG Pei-yan.Interfacial stress analysis of beams strengthened with a prestressed CFRP plate [J].Engineering Mechanics，2009，26(7)：78-82，88.

[10]WU X F，ZHAO Y H.Stress-function variational method for interfacial stress analysis of adhesively bonded joints [J].International Journal of Solid and Structures，2013，50(25/26)：4305-4319.

[11]WU X F，JENSON R A.Stress-function variational method for stress analysis of bonded joints under mechanical and thermal loads [J].International Journal of Engineering Science，2011，49(3)：279-294.

[12]EDALATI M，IRANI F.Interfacial stresses in RC beams strengthened by externally bonded FRP/steel plates with effects of shear deformations [J].Journal of Composites for Construction，2012，16(1)：60-73.

[13]喻溅鉴，周储伟.复合材料疲劳分层的界面单元模型 [J].复合材料学报，2009，26(6)：167-172.

YU Jian-jian，ZHOU Chu-wei.Interface element model for fatigue delamination analysis of composites [J].Acta Materiae Compositae Sinica，2009，26(6)：167-172.

[14]中国铁道科学研究院.京津城际铁路CRTS II型板式无砟轨道设计原理与方法总结 [R].北京：中国铁道科学研究院，2008.

[15]ZHANG L，TENG J G.Finite element prediction of interfacial stresses in structural members bonded with a thin plate [J].Engineering Structure，2010，32(2)：459-471.

[16]STEPHEN J，XIA L，RAVINDRA D，et al.A discrete damage zone model for mixed-mode delamination of composites under high-cycle fatigue [J].International Journal of Fracture，2014，190(1/2)：53-74.

[17]XU X P，NEEDLEMAN A.Numerical simulations of dynamic crack growth along an interface [J].International Journal of Fracture，1996，74(4)：289-324.

Supported by the National Natural Science Foundation of China(51378503)

Numerical Stimulation of Interface Delamination Failure for Prefabricated Slab Ballastless Track

DAIGong-lian1,2SUMiao1

(1. School of Civil Engineering，Central South University，Changsha 410075，Hunan，China；2. National Engineering Laboratory for High Speed Railway Construction，Changsha 410075，Hunan，China)

Firstly，the failure mode and adhesive mechanism of interface between different layers of ballastless track were analyzed by simplifying temperature load into the shear load of track slab. Then，on the basis of constructive cohesive force model and experimental bond strength parameters of cement asphalt mortar，an interface finite element model of ballastless track structure was established. Finally，the evolution rules of interfacial stress，interfacial bond bearing capacity，interfacial relative displacement and interfacial cracks under the action of shear load were investigated. The results show that (1) both interfacial shear stress and normal stress distribute unevenly and achieve their maximums at the ends of track slab，and interfacial normal stress may result in a tension of track slab at two ends of the slab； (2) under the action of shear load，the interface fails gradually as a result of the interfacial shear stress exceeding the maximum bond strength，and the maximum interfacial bond bearing capacity is 264.8 kN； (3) the longitudinal displacement of track slab relatively to mortar-filling layer increases continuously with the shear load and then longitudinal cracks appear； and (4) the relative vertical opening displacement decreases after the interface has been cracked，followed with an interfacial shear fracture which may result in the delamination of ballastless tracks.

ballastless track； shear load； interface； crack； failure； finite element model； bond strength； relative displacement

1000-565X(2016)07-0102-06

2015-11-04

国家自然科学基金资助项目(51378503)；中国铁路总公司重点课题(2014G001-D)；湖南省研究生科研创新项目(CX2015B050)

戴公连(1964-)，男，教授，主要从事大跨度桥梁极限承载力研究.E-mail：daigong@vip.sina.com

粟淼(1989-)，男，博士生，主要从事复合材料力学研究.E-mail：sumiao@csu.edu.cn

U 213doi： 10.3969/j.issn.1000-565X.2016.07.016