偏置面齿轮的碟形砂轮磨齿及啮合性能*

付学中　方宗德　李建华　侯祥颖

(西北工业大学 机电学院，陕西 西安 710072)



偏置面齿轮的碟形砂轮磨齿及啮合性能*

付学中方宗德李建华侯祥颖

(西北工业大学 机电学院，陕西 西安 710072)

采用碟形砂轮磨齿展成偏置面齿轮，通过碟形砂轮齿廓修形及控制砂轮中心运动实现偏置面齿轮齿面拓扑修形，建立了偏置面齿轮的磨齿和啮合坐标系，推导了拓扑修形偏置面齿轮齿面方程，建立了考虑安装误差的拓扑修形偏置面齿轮轮齿接触分析、承载接触分析模型，并编制了相应计算机程序，最后通过算例进行了分析.算例分析表明：碟形砂轮磨削偏置面齿轮是可行的；偏置面齿轮齿面几何不对称，偏置影响接触印痕、承载传动误差，但不影响几何传动误差；对偏置面齿轮拓扑修形，可有效改善偏置面齿轮副啮合性能.

偏置面齿轮；碟形砂轮；磨齿；拓扑修形；接触分析；几何传动误差；啮合性能

偏置面齿轮传动是圆柱齿轮与平面齿轮两轮轴线交错啮合的角度传动[1].目前面齿轮在国外已成功应用于多种武装直升机(如阿帕奇AH-64)的主减分扭传动中，性能优势明显，潜力巨大[2-4].偏置面齿轮应用于空间受限的航空动力传动系统中，可满足其多样化结构布局要求，进一步提升面齿轮在航空领域的优势，也可用于一般工业中，如代替汽车后桥差速器中的准双曲面齿轮传动.

目前，国内外关于偏置面齿轮的公开文献较少，且现有研究多集中在偏置面齿轮齿面设计和几何接触分析[5-8].面齿轮可通过插齿[9-10]、蜗杆滚刀滚齿、蜗杆砂轮磨齿等加工[11-12]；但插齿获得的齿面精度较低，无法满足航空传动高精度要求，而蜗杆曲面受奇异性限制，且滚刀和砂轮制造复杂，砂轮磨损后的修整困难，受制于我国现有磨齿技术和制造装备，国内面齿轮加工精度还不高.采用碟形砂轮磨削面齿轮，虽然加工效率较低，但砂轮的结构简单，利于设计、制造、修整，且对面齿轮设计参数无限制[13].

文中采用碟形砂轮磨齿展成偏置面齿轮，通过碟形砂轮的齿廓修形和控制砂轮中心的运动轨迹实现偏置面齿轮齿面拓扑修形，根据磨齿原理和空间啮合理论，推导拓扑修形偏置面齿轮齿面方程，建立考虑安装误差的拓扑修形偏置面齿轮接触分析模型，研究其啮合特性.

1　偏置面齿轮碟形砂轮磨齿

1.1磨齿原理

碟形砂轮磨削偏置面齿轮原理见图1，砂轮的轴截面与面齿轮轴z2间的距离为E，称为偏置距.磨削时存在3种运动关系：砂轮以速度ωs绕虚拟插齿刀轴zs旋摆模拟插齿刀回转，砂轮的旋摆与面齿轮以速度ω2绕轴z2的回转构成展成运动，砂轮与虚拟插齿刀的中心距为Eg；砂轮绕轴xg的高速自转构成切削运动；进给运动则是砂轮中心沿平行于虚拟插齿刀轴zs的往复移动，若砂轮中心沿非直线，例如沿图中抛物线g移动，则可控制偏置面齿轮的齿向修形.碟形砂轮磨削偏置面齿轮属双参数包络，双参数分别为砂轮绕虚拟插齿刀轴zs的转角φg、砂轮中心的移动距离lg，但3种运动是相互独立的，故可简化机床传动链，这与蜗杆砂轮磨齿时3种运动相互关联是有区别的.

图1偏置面齿轮磨齿

Fig.1Grinding offset face gear by disk wheel

1.2偏置面齿轮齿面

碟形砂轮磨削偏置面齿轮坐标系见图2.动坐标系Sg、Ss、S2分别固联砂轮、虚拟插齿刀、偏置面齿轮，辅助坐标系Sm、Sr、Sk、Sp均固联机架，其中Sm由Ss绕轴zs顺时针转φg得到，Sk由Sm沿轴zm负方向平移(平移距离为线段OkOm的长度)得到，Sr由Sk绕轴xk顺时针转γm得到，Sp由S2绕轴z2顺时针转φ2得到.偏置面齿轮齿面Σ2是砂轮齿面Σg在S2中的包络，而Σg为虚拟插齿刀端面截线的回转曲面.若以acs、ucs表示齿条刀齿廓抛物线修形参数，则虚拟插齿刀为失配的渐开线齿廓，Σg为失配的渐开线回转曲面，彭先龙等[14]对此有详细论述.图中ag、lg0为砂轮中心沿抛物线g移动时的参数，a为抛物线g所在平面与砂轮轴截面ygzg间的有向角(一般取0)，这3个参数即为偏置面齿轮齿向修形参数.偏置面齿轮转角φ2与砂轮转角φg满足φ2=φgm2s，m2s是虚拟插齿刀与偏置面齿轮的齿数比，夹角γm是z2、zs轴夹角γ的补角，两回转轴的公垂线OpOk即为偏置距E，线段OkOm用L0表示，E、L0与偏置面齿轮内外径L1、L2关系为E2+L02=(L1+L2)2/4.

偏置面齿轮齿面Σ2位矢R2和法矢n2表示为

(1)

n2(us，lg，φg，θg)=L2g(lg，φg)ng(us，θg)

603 术前糖类抗原 19-9 水平评估不同甲胎蛋白水平肝细胞癌肝切除术后患者的预后 李风伟，邹奇飞，薛 辉，项红军，夏 勇，李 俊，阎振林，沈 锋，王 葵

(2)

式中：Rg、ng为砂轮位矢和法矢，具体求解见文献

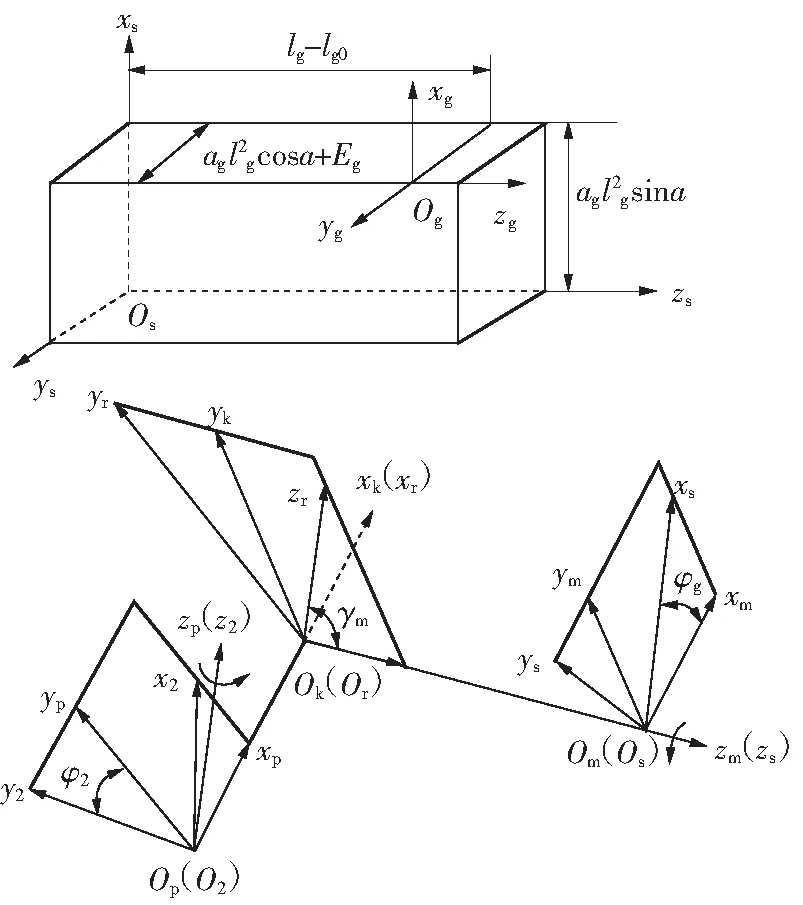
图2偏置面齿轮磨齿坐标系

Fig.2Coordinate systems for offset face gear

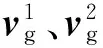
(3)

M2g按下式确定

M2g=M2pMpkMksMsg

(4)

(5)

(6)

(7)

(8)

2　轮齿接触分析(TCA)

轮齿接触分析时采用的坐标系见图3，坐标系S1、S2分别固联直齿圆柱小轮、偏置面齿轮，φ1、φ2为转角，两齿面在固定坐标系Sf中切触.坐标系Sq、Se、Sd分别用来模拟轴向位移误差Δq、偏置误差ΔE、轴夹角误差Δγ，B为小轮与虚拟插齿刀分度圆半径之差，γf是实际安装轴夹角，γf=γm+Δγ.偏置面齿轮副在Sf中切触方程可表示为

(9)

式中：R1、n1为小轮位矢和法矢；u1、l1是展成小轮的齿条刀曲面坐标参数[15]；Mf2、Mf1分别表示由S2到Sf、S1到Sf的变换矩阵；Lf2、Lf1为Mf2、Mf1的底矢变换矩阵.Mf2按下式确定

(10)

(11)

(12)

(13)

(14)

将式(9)向坐标轴投影，可得5个独立的标量方程，式中共8个参数，联立啮合方程f1、f2可消去lg、φg2个参数，以固定步长取一系列Φ2为输入量求解式(9)，将解出的参数us、θg代入式(1)得到啮合迹线，并根据下式求解几何传动误差：

ΔΦ2=Φ2-Φ20-N1/N2(Φ1-Φ10)

(15)

式中，Φ10、Φ20是两齿面初始转角，N1、N2是两轮齿数.

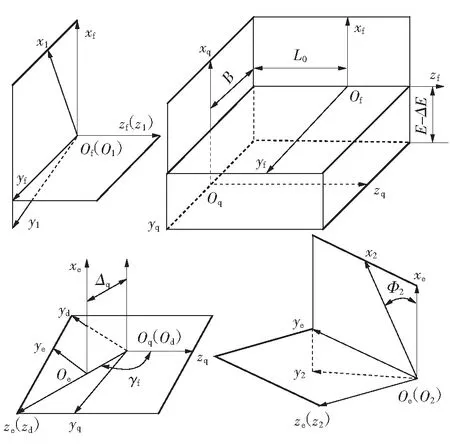
图3啮合坐标系

Fig.3Coordinate systems for gear meshing

3　承载接触分析(LTCA)

在TCA基础上需进一步求解任意接触点两齿面相对主方向，确定离散接触点对的间隙、沿接触椭圆长轴方向离散点的柔度矩阵，算法见文献[16-17].建立考虑安装误差的偏置面齿轮副承载接触问题的数学规划模型：

(16)

上述非线性规划是由已知参数F、w、P和未知参数p、Z、d组成，Xj(j=1，2，… 2n+1)为人工变量；F为齿面法向柔度矩阵，采用有限元法计算；p为瞬时接触椭圆长轴离散点处法向载荷；Z为轮齿变形后的法向位移；d为瞬时接触椭圆长轴离散点处变形后的齿面间隙；X=[X1X2…X2n]T，n维列向量；w为偏置面齿轮齿面间n维初始间距矢量，由TCA得到；P为齿面上的集中载荷；e的各元素均为1.上式目标函数为变形能最小，-Fp+Z+d+X=w、P=eTp+X2n+1分别为变形后位移协调方程、力平衡方程，约束条件包括：边界条件为pj≥0、dj≥0、Zj≥0、Xj≥0和非嵌入条件pj=0║dj=0.求解数学规划(式(16))，由此可得承载传动误差(将Z转换为角度值)、齿面载荷分布等.

4　实例分析

由上述推导编制计算机程序并输入设计参数仿真：大、小轮齿数为100、20，虚拟插齿刀齿数为23，压力角为25°，模数为2mm，轴夹角γ为90°，面齿轮内外径L1、L2为97、107mm.为减小砂轮磨损速度及提高磨齿效率，中心距Eg应尽可能大，文中取150mm.偏置面齿轮的数字齿面见图4，说明碟形砂轮磨削偏置面齿轮是可行的，为方便叙述规定图中左、右侧齿面.

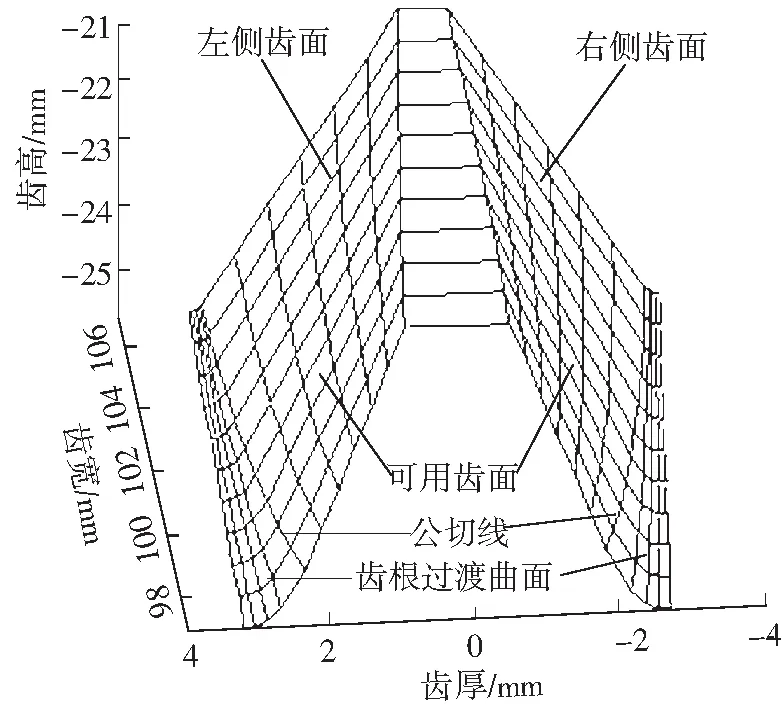
(a)E=5mm

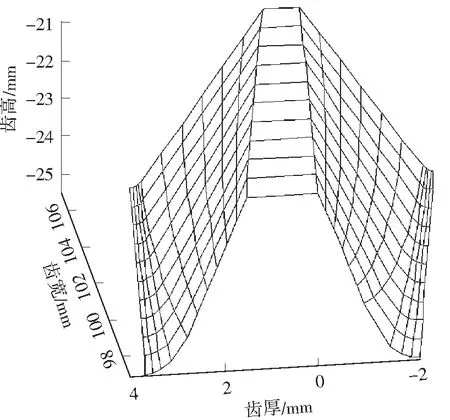
(b)E=15mm

由图可见，各偏置面齿轮轮齿均不存在内径根切和外径变尖现象；随着偏置距的增大，面齿轮轮齿左、右侧齿面几何不对称加剧.无载时对准安装条件下偏置面齿轮副的TCA结果见图5-7.

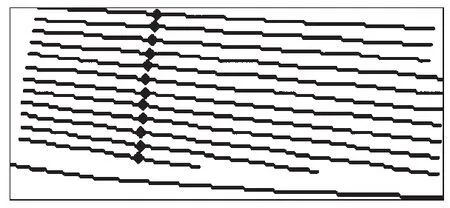
(a)E=5mm，左侧齿面

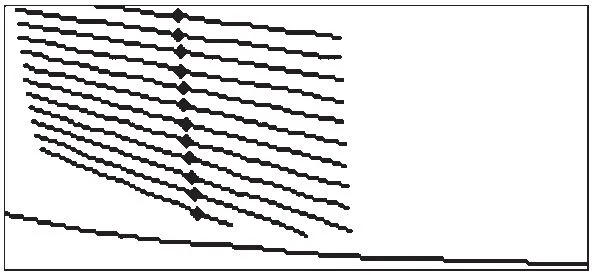
(b)E=5mm，右侧齿面

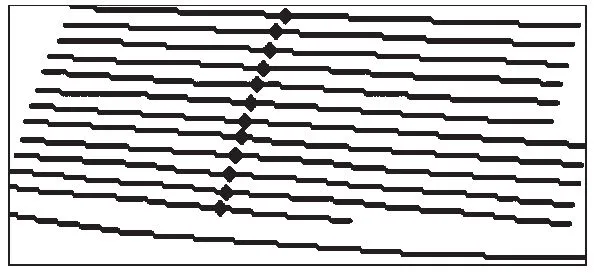
(c)E=15mm，左侧齿面

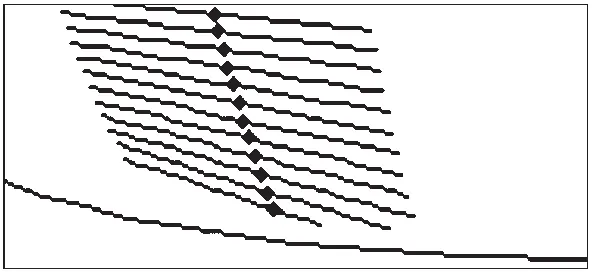
(d)E=15mm，右侧齿面

由图5可知，偏置面齿轮副接触迹线与齿根成一定角度倾斜，倾斜方向在左、右侧齿面上是相反的，这与图6所示E=0mm，即相交面齿轮接触迹线近似垂直齿根有明显区别，且偏置距越大，接触迹线越倾斜，并越向外端移动.对比左、右侧齿面接触印痕可知，右侧齿面接触椭圆长轴较左侧倾斜；左侧齿面接触椭圆长轴较长，右侧较短，故应尽量选左侧齿面为工作齿面.由图7可知，偏置面齿轮副几何传动误差始终为0(线Ⅰ)，即偏置不影响几何传动误差.

图7中线Ⅱ对应拓扑修形参数acs=-0.001 5、ucs=0.6mm、ag=-0.000 4、lg0=-2mm，E=15mm，工作齿面为左侧齿面，可见偏置面齿轮拓扑修形能获得抛物线几何传动误差，此时接触迹线变长并外移，见图8中路径Ⅰ，经计算有效重合度较无修形从1.375提高到1.5；当存在安装误差Δq=0.14mm时，接触迹线进一步外移，见图8中路径Ⅱ.

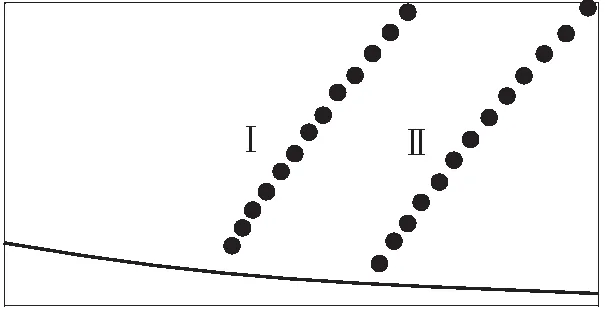
图8偏置面齿轮(E=15mm)接触迹线

Fig.8Contactlinesofoffsetfacegear(E=15mm)

对准安装条件下承载100N·m时各偏置面齿轮承载传动误差见图9，Ⅰ、Ⅱ、Ⅲ依次对应E=0,5,15mm，其误差波动幅值分别为14.00″、14.26″、15.56″，可见偏置距越大，承载传动误差波动幅值越大.偏置面齿轮(E=15mm)拓扑修形后，误差波动幅值由15.56″降到6.91″，如线Ⅳ所示，可见偏置面齿轮拓扑修形可有效减小承载误差波动幅值.

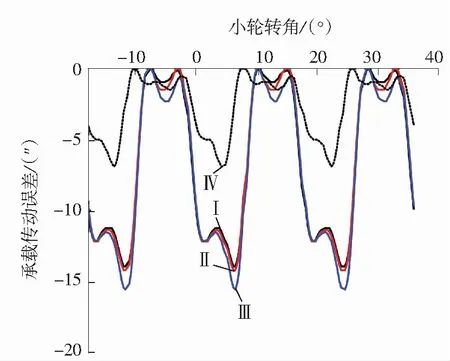
图9对准安装承载传动误差

Fig.9Loadtransmissionerrorsincaseofnomisalignment

对准安装载荷分布如图10所示.图10表明偏置面齿轮副(E=15mm)承载100N·m在无修形及拓扑修形时，每条接触椭圆长轴上的载荷均从轮齿中部沿接触椭圆长轴向两端逐渐减小为零，齿面载荷分布变化较均匀、平缓.

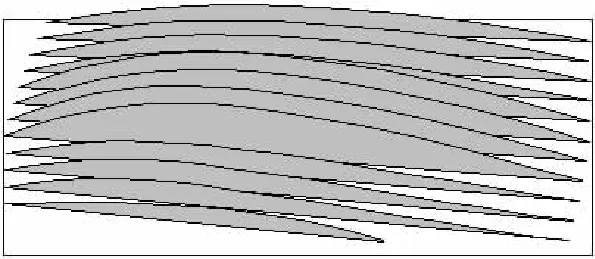
(a)无修形

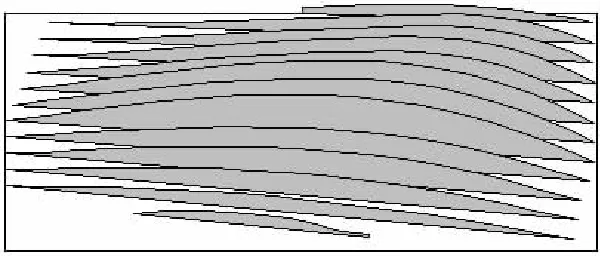
(b)拓扑修形

5　结论

(1)推导了碟形砂轮展成拓扑修形偏置面齿轮齿面方程，建立了考虑安装误差的拓扑修形偏置面齿轮副TCA、LTCA模型，并编制了相应计算机程序.

(2)对碟形砂轮磨齿展成偏置面齿轮齿面进行了数值仿真并可视化，说明碟形砂轮磨削偏置面齿轮是可行的.

(3)偏置面齿轮副接触分析表明，偏置距越大，接触迹线越倾斜、外移，承载传动误差波动幅值越大，但几何传动误差始终为零.

(4)通过碟形砂轮齿廓修形及控制砂轮中心运动对偏置面齿轮拓扑修形，可有效改善偏置面齿轮副啮合性能.

[1]BOSSLERRB.Offsetfacegeartransmission：5178028 [P].1993-01-12.

[2]GABICCINIM，GUIGGIANIM，PUCCIOFD.Geometryandkinematicsoffacegearsmatingwithahelicalinvolutepinion[C]∥Proceedingsofthe11thWorldCongressinMechanismandMachineScience.Tianjin：IFTOMM，2004.

[3]FILLERRR，HEATHGF，SLAUGHTERSC，etal.Torquesplittingbyaconcentricfacegeartransmission[R].Montreal：theAmericanHelicopterSociety58thAnnualForum，2002.

[4]BARONES，BORGIANNIL，FORTEP.Evaluationoftheeffectofmisalignmentandprofilemodificationinfacegeardrivebyafiniteelementmeshingsimulation[J].JournalofMechanicalDesign，2004，126(5)：279-288.

[5]ZHANGY，WUZ.Offsetfacegeardrives：toothgeometryandcontactanalysis[J].JournalofMechanicalDesign，1997，119(1):114-119.

[6]LITVINFL，EGELJAA，TANJ，etal.Computerizeddesign，generationandsimulationoforthogonaloffsetface-geardrivewithaspurinvolutepinionwithlocalizedbea-ringcontact[J].MechanismandMachineTheory，1998，33(1/2)：87-102.

[7]朱如鹏.面齿轮传动的啮合特性研究 [D].南京：南京航空航天大学机电学院，2000.

[8]魏冰阳，袁群威，吴聪.偏置正交面齿轮的几何设计及三维造型 [J].河南科技大学学报(自然科学版)，2012，33(3)：31-34.

WEI Bing-yang，YUAN Qun-wei，WU Cong.Design and gear shaping experiment on offset orthogonal face-gear [J].Journal of Henan University of Science & Technology(Natural Science)，2012，33(3)：31-34.

[9]沈云波.面齿轮传动齿面设计理论及插齿技术研究 [D].西安：西北工业大学机电学院，2009.

[10]LITVIN F L，GONZALEZ P I，FUENTES A，et al.Design，generation and stress analysis of face-gear drive with helical pinion [J].Computer Methods in Applied Mechanics & Engineering，2005，194(36/37/38)：3870-3901.

[11]LITVIN F L，FUENTES A.Gear geometry and applied theory [M].New York：Cambridge University Press，2004.

[12]郭辉.面齿轮滚齿加工方法及其啮合性能研究 [D].西安：西北工业大学机电学院，2009.

[13]STADTFELD H J.Coniface face gear cutting and grinding [EB/OL].(2011-06-20) [2015-10-12].http：∥www.gearsolutions.com/article/detail/6020/coniface-face-gear-cutting-and-grinding.

[14]彭先龙，方宗德，苏进展，等.采用碟形砂轮的面齿轮磨齿方法理论分析 [J].航空动力学报，2012，27(5)：1159-1165.

PENG Xian-long，FANG Zong-de，SU Jin-zhan，et al.Theory analysis for application grinding disk in face gear grinding [J].Journal of Aerospace Power，2012，27(5)：1159-1165.

[15]李玮，王丹，付学中.变位面齿轮副小轮双向修形轮齿接触分析 [J].机械传动，2015，39(5)：46-47.LI Wei，WANG Dan，FU Xue-zhong.Tooth contact analy-sis of profile-shifted face gear drives with double-crowned Pinions [J].Journal of Mechanical Transmission，2015，39(5)：46-47.

[16]方宗德.修形斜齿轮的承载接触分析 [J].航空动力学报，1997，12(3)：251-254.

FANG Zong-de.Loaded tooth contact analysis of modified helical gears [J].Journal of Aerospace Power，1997，12(3)：252-254.

[17]赵宁，郭辉，方宗德，等.直齿面齿轮修形及承载接触分析 [J].航空动力学报，2008，23(11)：2142-2146.

ZHAO Ning，GUO Hui，FANG Zong-de，et al.Modification and loaded contact analysis of spur face gear [J].Journal of Aerospace Power，2008，23(11)：2142-2146.

Supported by the National Natural Science Foundation of China(51375384)

Grinding and Meshing Performance of Offset Face Gear Modified with Disk Wheel

FUXue-zhongFANGZong-deLIJian-huaHOUXiang-ying

(School of Mechanical Engineering，Northwestern Polytechnical University，Xi’an 710072，Shaanxi，China)

Firstly，an offset face gear was generated by using a disk wheel，and the topological modification of the gear was achieved through disk wheel’s profile modification and center movement control. Secondly，the coordinate systems for grinding and meshing were established，and tooth surface equations of the gear were deduced. Then，by taking into consideration misalignment and topological modification，computational models for tooth contact analysis and loaded tooth contact analysis of the offset face gear pairs were established，and the corresponding computer program was developed. Finally，some examples were given. The results show that (1) the method of grinding offset face gear with disk wheel is feasible； (2) the tooth surface of the offset face gear is geometrically asymmetrical，and the offset value has an effect on contact patch as well as loaded transmission error but has little influence on transmission error； and (3) the meshing performance of offset face gear pairs can be effectively improved by means of topological modification of the offset face gear.

offset face gear； disk wheel； grinding； topological modification； contact analysis； transmission error； meshing performance

1000-565X(2016)07-0077-06

2015-10-13

国家自然科学基金资助项目(51375384)

付学中(1986-)，男，博士生，主要从事面齿轮设计制造研究.E-mail：fxzysu@163.com

TH 132.41doi： 10.3969/j.issn.1000-565X.2016.07.012