复系数Riccati微分方程解的存在条件及应用

王明建， 胡　博， 王桂花

(1.郑州师范学院 数学与统计学院,郑州 450044； 2.河南工业大学 理学院,郑州 450002)



复系数Riccati微分方程解的存在条件及应用

王明建1， 胡博2， 王桂花1

(1.郑州师范学院 数学与统计学院,郑州 450044； 2.河南工业大学 理学院,郑州 450002)

对于系数是复常数的Riccati微分方程，y′=py2+qy+r，其中p=a+bi，q=c+di，r=e+fi是复数，a,b,c,d,e,f∈R，i是虚单位，且pr≠0，得到了此类方程解存在的一些条件，并给出了相关的应用.

复常数；Riccati微分方程；解存在条件；应用

众所周知，非线性Riccati微分方程

(1)

(其中P(x)、Q(x)和R(x)都是定义域D上的连续可微函数，且P(x)R(x)≠0)一般没有初等积分解法[1～6]，通常求通解的途径是：如果能预先得到式(1)的一个特解y0，再利用初等变换y=u+y0，使之变为Bernoulli方程再求解.然而求式(1)一个特解的难度并不亚于求其通解.虽然文[2]用不同的方法求得Riccati微分方程的特解甚至通解，但对系数是复常数的Riccati微分方程，却没有论及，本文讨论了一类系数为复常数的Riccati微分方程

(2)

(其中p=a+bi，q=c+di，r=e+fi是复常数，a,b,c,d,e,f∈R，i是虚单位)的解的存在条件及解的求法，为寻求复系数Riccati方程的解提供了有效的方法，并给出相关的一些应用.

1　主要结果及证明

首先不加证明地给出以下两个引理：

(3)

如果P(x)=p、Q(x)=q和R(x)=r都是复常数，作为特例，有

(4)

只要熟悉微分方程解的存在唯一性定理，则有

定理1如果设f(x,y)=py2+qy+r，方程(2)中的系数是复常数，并且关于变量y满足Lipschitz条件，即不等式

|f(x,y1)-f(x,y2)|≤(|p||y1+y2|+|q|)|y1-y2|，

(5)

在矩形域D上恒成立，那么方程(2)存在唯一解y=φ(x)，它在D上连续，且满足初始条件y0=φ(x0)，其中|p|，|q|表示复数的模.

定理2方程(2)存在通解

(6)

的充要条件是s=0，其中C为任意常数.

(7)

q2-4pr=0

(8)

注：式(8)的右端具有Δ=b2-4ac的形式.

定理4方程(2)有特解y=c(常数)的充要条件是

pc2+qc+r=0

(9)

证明必要性显然，只证充分性.在(2)中，令y=c，有

(10)

注：式(9)可以作为方程(2)的示性方程.

2　应用举例

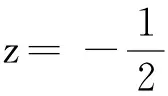
[1]王高雄.常微分方程[M].第3版.北京:高等教育出版社,2006.

[2]王明建.Riccati微分方程特解的新求法[J].数学的实践与认识,2006(7):172-175.

[3]丁同仁.常微分方程教程[M].北京:高等教育出版社,1991:5.

[4]都长青.常微分方程(修订版)[M].北京:高等教育出版社,1992.

[5]庄万.常微分方程习题与解答[M].北京:高等教育出版社,1999.

[6]A·Φ·菲利波夫.常微分方程习题集[M].孙广成,张德厚译.上海:上海科学技术出版社,1981.

[责任编辑王新奇]

The Existence Condition and Application of the Solution ofRiccati Differential Equation with Complex Coefficient

WANG Ming-jian1, HU bo2, WANG Gui-hua1

(1.DepartmentofMathematics,ZhengzhouNormalUniversity,Zhengzhou450044,China; 2.CollegeofScience,HenanUniversityofTechnology,Zhengzhou450002,China)

Inthispaper,fortheRiccatidifferentialequationofy′=py2+qy+rwithcomplexcoefficient,amongthemp=a+bi，q=c+diandr=e+fiarecomplexnumbers, a,b,c,d,e,f∈R，iisavirtualunitandpr≠0.Someconditionsfortheexistenceofsolutionsoftheseequationsareobtained,andtherelatedapplicationsaregiven.

complexcoefficient;Riccatidifferentialequation;solutionexistencecondition;application

1008-5564(2016)03-0034-03

2016-01-18

国家自然科学基金项目(11161018)

王明建(1958—)，男，河南荥阳人，郑州师范学院数学与统计学院教授，主要从事动力系统研究.

O175.5

A