脑电信号的特征提取方法

胡文凤, 宋江玲, 张　瑞

(西北大学 数学学院，西安 710127)



脑电信号的特征提取方法

胡文凤, 宋江玲, 张瑞

(西北大学 数学学院，西安 710127)

癫痫是一种常见的发病率极高的慢性脑疾病，全球约有1%的人口患有癫痫.传统的癫痫性发作检测主要依赖于临床医生对脑电图进行视觉上的检查，并结合临床经验给出诊断.但海量的脑电数据使得这一传统方法不仅十分耗时，而且主观性很强.因此，开展癫痫性发作自动检测的研究以辅助医生完成癫痫性发作检测具有重要的临床意义.而如何从脑电图中提取合适的脑电特征以及如何选取恰当的分类器是完成癫痫性发作自动检测的关键环节，其中如何从脑电图中提取出能够区别发作脑电与未发作脑电特征是首先的也是最为重要的一步.总结了三种常见的用于癫痫性发作自动检测的基于非线性相似性的脑电特征提取方法，通过分析其优缺点，给出相应的改进建议.

癫痫；癫痫性发作；癫痫性发作的自动检测；非线性动力学；基于顺序模式的非相似性；模糊相似性指数；基于巴氏距离的非相似性

癫痫是一种常见的，发病率仅次于中风的第二大慢性脑疾病[1].癫痫性发作是由大脑局部区域的大量神经元超同步异常放电所产生，临床表现为短暂的感觉障碍、肢体抽搐、意识丧失、行为障碍等，严重威胁着人们的正常生活乃至生命.脑电图(electroencephalographic, EEG)是大脑电活动的记录，它蕴含着丰富的生理及病理信息[2].从生理角度来讲，不同的脑电图对应于受体不同的生理活动(如静坐、走动、跑跳等)；从病理角度来讲，不同的脑电图蕴含着不同的病理信息(如癫痫、阿尔茨海默病等).

传统的癫痫性发作检测主要是依靠医生对患者的脑电图进行视觉检查并结合临床症状进行综合诊断而完成.然而长时程的脑电图监测所产生的海量脑电数据，使得这一诊断方法不仅十分耗时而且主观性很强.基于传统检测方法的局限性，开展癫痫性发作自动检测技术的研究就具有重要的临床应用价值.其本质在于通过计算机技术及机器学习方法完成对脑电图的分析进而得出相应的辅助诊断结果.

由于EEG中所蕴含信息的广度及深度，癫痫性发作自动检测中一个重要步骤是通过恰当的方法将EEG中隐含的癫痫病理信息提取出来，这一过程称作特征提取.将所提取的特征分配给恰当的分类器以最终完成癫痫性发作的自动检测.如何从包含思想、情绪、行为、病理等因素的脑电信号中提取出能将癫痫发作与未发作脑电区别开来的特征，是一项具有挑战性但同时至关重要的工作.这一问题自1982年癫痫性发作自动检测被首次提出之时[3]，一直是学者们的研究重心.随着癫痫性发作自动检测技术的发展，大量的特征提取方法已被广泛提出.大体可以分为两类：一类是各状态下(发作与未发作)的特征值可以独立计算；另一类是各个状态的特征值是不可以独立计算.在这一情形下，我们往往需要提前设置一个参考状态，然后将所有的脑电片段与之进行相似性对比，进而根据对比结果得出特征.本文主要对非线性动力学意义下的几种刻画相似性的脑电特征提取方法进行系统阐述，通过分析其优缺点，给出相应的改进建议.

1　基于非线性度量的特征提取方法

1.1非线性动力学

非线性动力学是主要研究非线性动力系统(即动力系统的输出与输入满足非线性时的关系)中状态变量随时间变化情况的一门学科[4].

一个系统中全部可能状态变量的集合称为状态空间或相空间，但在许多情形下，一个系统中的所有状态变量或者状态变量之间的相互关系并非已知，因此往往需要对相空间进行重构，进而通过研究重构相空间来揭示动力系统的内在变化规律.

时间延迟方法是一种比较典型且常用的相空间重构方法.给定一个时间序列{Xn:n=1,2,…,Nn},矩阵A=(aij)m×N称为重构相空间(也称作信号Xn的轨迹矩阵)，其中

aij=xj+(i-1)τ

(1)

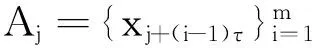
1.2基于顺序模式的非相似性

Ouyang等人于2010年提出基于顺序模式的非相似性(ordinalpatternbaseddissimilarity，OPBS)的概念[5]，其基本思想为：由于白噪声是一种完全随机的不包含任何信息的信号，那么对其进行顺序排列后，所有顺序模式是等概率出现的，从而所有状态变量的顺序模式也服从等概率出现.但对于包含一定信息量的信号，其状态变量的顺序模式应该是具有一定规律性，且对应不同含义信号的顺序模式应该是不同的.基于上述认知，Ouyang等人应用状态变量顺序模式的概率作为EEG的特征进行癫痫性发作自动检测.具体的算法总结如下：

步骤1：将原始EEG信号X={x1,x2,…,xnn}，划分为等长的脑电片段{Si:i=1,2,…,n}，每一Si中均包含l个样本点，即n=Nn/l.在所有Si中随机选取一个发作脑电作为参考信号，记作Sref.为方便起见，其余所有片段均称为当前信号，并记作St.

步骤2：利用公式(1)分别对当前信号St和参考信号Sref进行相空间重构，分别记作Xt和Xref，重构得到的这两个相空间中每一列即为相应的状态变量.

步骤5：定义OPBS为

其中Dm∈[0,1].当Dm=1时，则表示当前信号与参考信号完全不同；当Dm=0时，则表示两个信号完全相同.其中m的选取至关重要，太大或太小都不能体现全部的顺序模式.m的选取和片段的长度l有关，满足m!+(m-1)τ≪l[6].

1.3模糊相似性指数

动态相似性(dynamicalsimilarityindex，DSI)最早是用来刻画颞叶癫痫在发作前颅内脑电变化的特征提取方法.主要思想是通过对大脑不同状态下脑电信号相空间进行处理后，利用Heaviside函数计算不同状态间的相似性[7].而Heaviside函数是硬函数，即取值仅为1或0，基于此局限性，Ouyang等人提出模糊相似性的概念(fuzzysimilarityindex，FSI)[8]，其作为DSI的一种改进，主要是将Heaviside函数替换为高斯函数，FSI得到更多关注与应用.FSI的计算步骤如下：

步骤1：从X中选择一段连续300s长的未发作的EEG作为参考信号，记作Sref.对原始信号X进行划分，将划分结果记作S={S1,S2,…,Sn}，其中Si包含l个样本点，且保证其只代表一种状态(发作或未发作)，为了方便起见，我们将所有的Si均称为当前信号，记作St.

步骤2：利用公式(1)分别对当前信号St和参考信号Sref进行相空间重构，得到A(St)和A(Sref).

步骤3：为进一步降低噪声，通过奇异值分解(singularvaluedecomposition,SVD)将A(Sref)和A(St)分别投影到A(Sref)的主轴，得到X(Sref)和X(St).

步骤4： 从参考状态X(Sref)中随机抽取矩阵，记作Y(Sref),并计算

这里Nref和Nt分别是状态空间A(Sref)和A(St)的点的个数.r是需要确定的参数，一般取r为参考信号的累计临界分布的30%的上分位点[9].

步骤5:计算模糊相似度指数(FSI)

1.4基于巴氏距离的非相似性

基于巴氏距离的非相似性(bhattacharyyabaseddissimilarityindex,BBDI)是由Nikanazar于2010 年提出的一种基于FSI的改进方法[10].由于在计算FSI时需要确定参数r，而r的取值依赖于参考信号，需要在参考信号确定的基础上来进一步设定.而在BBDI中，状态空间的相似性最终由巴氏距离计算，进而避免了在FSI中参数r的选取，且该算法再无其他参数.BBDI的计算步骤如下：

步骤1：从X中随机选择一段连续的时长300s的未发作EEG作为参考信号，记作Sref.对原始信号X进行划分，将划分结果记作S={S1,S2,…,Sn}，其中包含l个样本点，且只代表一种状态(发作Si或未发作).为简单起见，我们将所有的Si均称为当前信号，记作St.

步骤2：利用公式(1)分别对当前信号St和参考信号Sref进行相空间重构，得到A(St)和A(Sref).

步骤3：为进一步降低噪声，通过奇异值分解将A(Sref)和A(St)分别投影到A(Sref)的主轴，得到X(Sref)和X(St).

步骤4：各脑电片段的统计分布的巴氏距离可表示为

这里mx(St)和mx(Sref)分别表示X(St)和X(Sref)的列均值，PX(St)和PX(Sref)分别为其对应的协方差矩阵.且

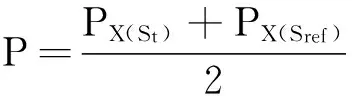
如果当前信号和参考信号越相似，则BBDI的值会较小；相反，BBDI的值会比较大.

回顾上述所有算法，它们面临的共同问题是如何确定嵌入维数m和时间延迟τ.不同的嵌入维数和时间延迟会对算法的性能产生很大的影响，目前已有许多方法被用来确定恰当的嵌入维数和时间延迟，例如用互信息法(Mutualinformation，MI)[11]确定时间延迟，Cao’s法[12]确定嵌入维数等，读者可查阅相关文献[13-14].

2　结语

本文主要介绍了3种基于非线性相似性度量的脑电特征提取方法.OPBS是对信号顺序模式的分析，基于包含不同信息的信号顺序模式间具有差异性这一认识，研究癫痫发作与未发作状态变量的顺序模式间的非相似性，以非相似性的大小来判断癫痫发作与否.FSI是对动力系统轨迹矩阵的分析，基于不同动力系统轨迹矩阵间具有差异性的认识，研究癫痫发作与未发作情况下轨迹矩阵间的相似性，从而对癫痫发作与否进行判断.BBDI是对FSI算法的一种改进.FSI在计算相似性时会涉及高斯函数中参数r的确定，而r的取值又依赖于参考信号本身.为了避免这一问题，Nikanazar提出了基于巴氏距离的非相似性算法，即BBDI.结合以上算法的介绍，可以考虑从以下两个方面对算法进行改进：(1) 对于顺序模式，考虑从顺序模式的分布意义着手，对其分布进行统计分析，然后计算统计特征间相似性；(2)对于轨迹矩阵，可以从矩阵变换和相似性两个角度考虑进行改进.

[1]KUMARTS,KANHANGADV,PACHORIRB.Classificationofseizureandseizure-freeEEGsignalsusinglocalbinarypatterns[J].BiomedicalSignalProcessing&Control,2015,15:33-40.

[2]RAYGC.Analgorithmtoseparatenonstationarypartofasignalusingmid-predictionfilter[J].IEEETransactionsonSignalProcessing,1994,42(9):2276-2279.

[3]GOTMANJ.AutomaticrecognitionofepilepticseizuresintheEEG[J].Electroencephalography&ClinicalNeurophysiology,1982,54(5):530-540.

[4]刘秉正,彭建华.非线性动力学[M].北京: 教育出版社,2004.

[5]OUNYANGGX,DANGCY,RICHARDSDA,etal.OrdinalpatternbasedsimilarityanalysisforEEGrecordings[J].ClinicalNeurophysiology,2010,121(5):694-703.

[6]AMIGOJM,KENNELMB.Topologicalpermutationentropy[J].PhysicaDNonlinearPhenomena,2010,231(231):125-145.

[7]QUYENMLV,MATTINERIEL,NAVARROV,etal.Adam.AnticipationofepilepticseizuresfromstandardEEGrecordings[J].TheLancet,2001,357:183-188.

[8]OUYANGG,LIX,GUANX.Useoffuzzysimilarityindexforepilepticseizureprediction[C].The5thWorldCongressonIntelligentControlandAutomation.Hangzhou,China,2004June; 14-18:5351-5535.

[9]QUYEN M,ADAM C,MARTINERIE J,et al.Spatiotemporal characterization of non-linear changes in intracranial activities prior to human temporal lobe seizures[J].European Journal of Neuroscience,2000,12:2124-2134.

[10]NIKNAZAR M,MOUSAVI S R,VOSOUGHI V B,et al.A new dissimilarity index on EEG signals for epileptic seizure detection[C].4th International Symposium on Communications,Control and Signal Processing (ISCCSP 2010) 2010： 1-5.

[11]FRASER A M,SWINNEY H L.Independent Coordinates for Strange Attractors from Mutual Information[J].Physical Review A,1986,33(2):1134-1140.

[12]CAO L.Practical method for determining the minimum embedding dimension of a scalar time series[J].Physica D: Nonlinear Phenomena,1997,110(1):43-50.

[13]王红礼,张琪昌,郭树起,等.非线性动力学理论及其应用[M].天津: 天津科学技术出版社,2002.

[14]SONG Y D,CROWCROFT J,ZHANG J X.Automatic epileptic seizure detection in EEGs based on optimized sample entropy and extreme learning machine[J].Journal of Neuroscience Methods,2012,210(2):132-146.

[责任编辑王新奇]

Method of Feature Extraction of EEG

HU Wen-feng, SONG Jiang-ling, ZHANG Rui

(Department of Mathematics, Northwest University, Xi’an 710127, China)

Epilepsy is a chronic neurological disorder disease, which affects approximately 1% of the world’s population. The traditional detection of epileptic seizures mainly depends on the clinical examination of the EEG, and makes the diagnosis based on clinical experience. However, the huge amount of EEG data makes this traditional method to be not only time consuming, but also highly subjective. Therefore, the study of automatic seizure detection method is important for clinical physicians to complete the detection of epileptic seizures. Designing an appropriate feature extraction method and how to selecting an efficient classifier are recognized to be crucial in the automatic seizure detection. Especially, how to extract the feature from EEGs, which can discriminate a seizure state and a non-seizure state, is the first and rather important step. In this paper, three common methods of EEG feature extraction based on nonlinear similarity for automatic detection of epileptic seizures are summarized, and the corresponding improvement suggestions are given by analyzing the advantages and disadvantages of these methods.

epilepsy; epileptic seizure; automatic detection of epileptic seizures; nonlinear dynamics; dissimilarity based on ordinal pattern; fuzzy similarity index; dissimilarity based on Bhattacharyya

1008-5564(2016)03-0021-04

2015-11-09

胡文凤(1990—)，女，内蒙古包头人，西北大学数学学院硕士研究生，主要从事癫痫自动检测技术的理论研究；

张瑞(1971—)，女，陕西西安人，西北大学数学学院教授，主要从事计算智能及信息技术研究.

O29

A