一种混合模型的闭环辨识方法

一种混合模型的闭环辨识方法

过程模型是实施先进控制的基础，基于系统的开环响应，进行过程模型辨识，是常用的辨识方法。因为开环系统只需持续激励，总是可辨识的。开环系统的输入信号与输出噪声不相关，经典的辨识方法可获得对象的一致无偏估计。

但出于生产安全或产品质量的考虑，很多工业过程不允许开环测试。闭环系统由于反馈的存在，噪声信息引入了系统，系统的输入输出具有相关性，常规的开环辨识方法结果往往是有偏的，甚至会导致模型不可辨识。针对这类问题，一些新算法相继提出，其中基于Box-Jenkins模型（B-J）的算法是一类应用较广的算法，B-J模型是一种过程模型和噪声模型相结合的参数模型，是解决包含有色噪声的辨识问题的一种有效方法。辨识混合B-J模型的有效方法之一是辅助变量（instrumental variable，IV）算法，它不但对低维对象有很好的辨识效果，对于高维的复杂过程以及包含有色噪声及非线性和时变类型的对象同样具有优势。

为实现基于工业生产运行数据而不进行测试进行闭环回路辨识，本文提出了一种基于混合Box-Jenkins模型和IV算法的闭环模型辨识算法。

闭环控制系统结构

工业控制系统的拉普拉斯域（s 域）闭环控制回路结构如图1所示，图中r （s）为回路的设定值，Gc（s）为控制器，u（s）为控制器输出，Gm（s）为过程模型，Gn（s）为干扰通道的传递函数，ξ（s ）为有色噪声，w（s）为均值0方差σ2的高斯白噪声，y （s）为系统输出，式中的s 为拉普拉斯算子。

由经典控制理论可知，图1所示的工业对象可表示为线性稳定的单输入单输出系统，系统可由以下公式来描述：

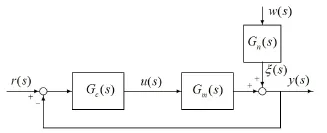
图1 闭环控制回路结构图

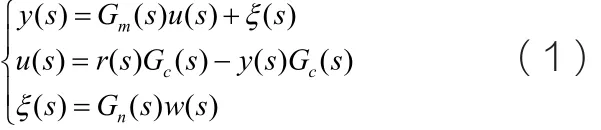
过程模型Gm（s）定义为：

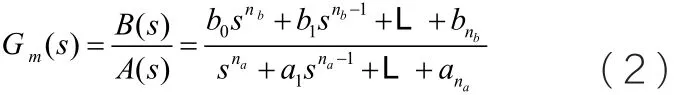
式中ai， i=1，L ，na和bi， i=0，L ，nb为模型参数，nb和na分别为传递函数的分子与分母的阶次且na≥nb。

s 域所对应的时域过程模型可表示为：

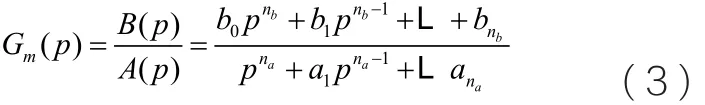
这里Gm（p）为过程模型Gm（s）的对应时域模型，p 为对应的时域算子。

为计算的方便性，而不涉及到过多的理论推导，干扰模型Gn（s）以ARMA模型表示，所对应的时域传递函数为：

式中z-1为后移算法子，满足z-1ξ（k）=ξ（k-1），di， i=1，L ，nd和ci， i=0，L ，nc为模型参数系数，nd和nc分别为噪声模型Gn的分子与分母阶次。这一模型可以使用基于IV算法的IVARAM算法进行辨识。

另外时域控制器模型表示为：

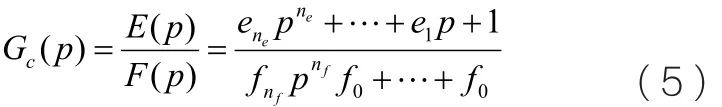
式中ei， i=1，L ，ne和fi， i=0，L ，nf为控制器参数系数，ne和nf分别为控制器模型Gc的分子与分母阶次。

基于辅助变量的混合B-J模型辨识

为解闭环回路中输入输出中因反馈噪声的存在造成过程模型辨识的有偏性问题，Young等提出了基于辅助变量的混合B-J模型辨识（CLRIVC）算法。算法通过定义一个新的预滤波器，解决了连续时间辨识输入输出数据的求导问题。算法基以y（ tk）和计算得到的u（ tk）的预滤波数据建立过程向量；基于公式（15）?计算不含循环噪声成份的x（tk）和v（tk），以x（tk）和v（tk）的预滤波数据建立辅助向量，应用公式（18）迭代求混合B-J模型。预滤波器具有如下形式：

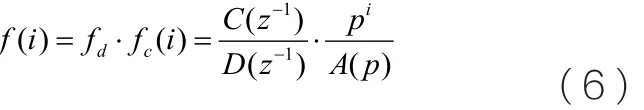
对于下式所示的时域闭环混合B-J模型：

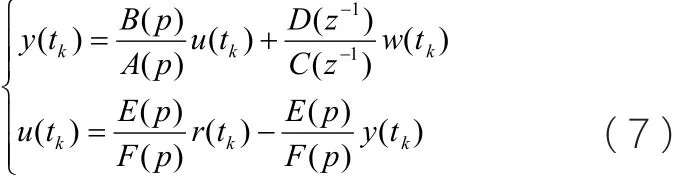
基于预测误差最小化，第k 个采样时刻的误差函数可表示为：

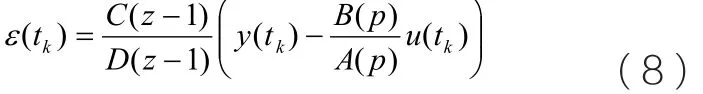
公式的预滤波形式为：

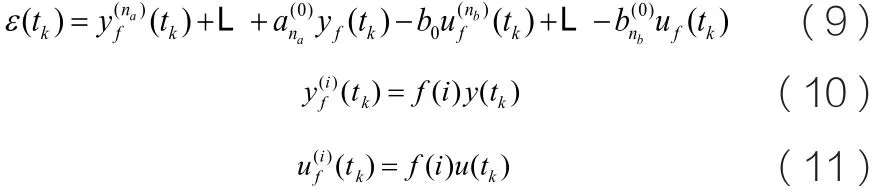
公式（9）的预滤波线性回归表达式可表示为：

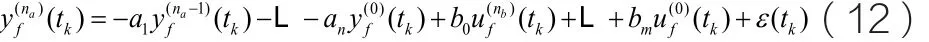
其向量参数表达式为：

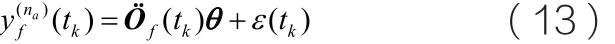
其中：

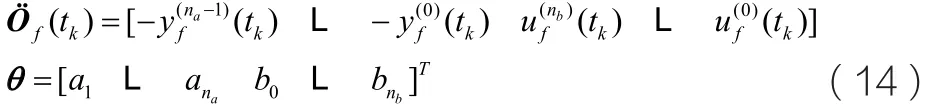
图形1所示闭环系统的无干扰过程时域模型可由下式计算出：

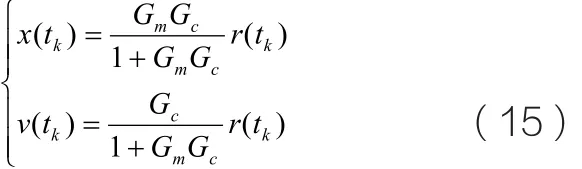
其预滤波形式可由下式得出：

公式（15）的预滤波辅助变量模型表达式为

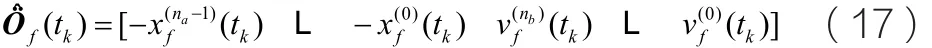
最终的辅助变量优化公式如下所示：

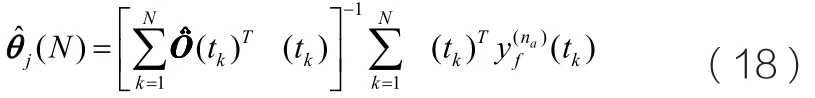
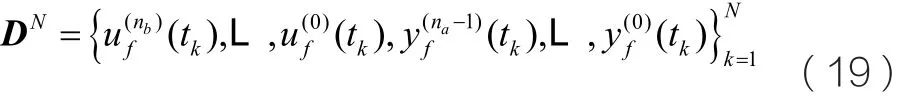
反馈噪声消除的闭环辨识算法

CLRIVC实现了闭环混合B-J模型闭环辨识，但过程模型的初始值偏离真值较远时，有时会出现收敛性差的问题。在分析图1结构的基础上，本文提出了新的消除反馈噪声的混合B-J模型闭环辨识改进算法（DNIV）。新算法将原来算法中的由过程输入输出的预滤波数据作为过程模型向量更新为不含反馈噪声成分的过程输入输出预滤波数据作为过程模型向量。

对于 图1所示的时域闭环模型方程可推导出：

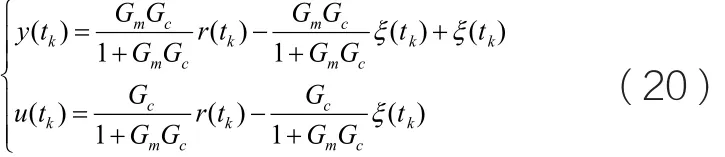
令：

由公式（15）、公式（20）和公式（21）可推导出：

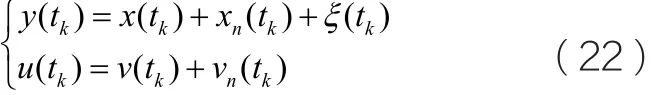
由公式（21）可知，vn（tk）为反馈噪声产生的控制器输出，为干扰产生的过程模型输出成份。

将公式（22）中u（tk）代入过程模型：

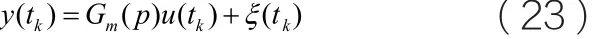
推导出不含反馈噪声成份的过程模型：

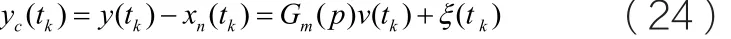
新算法以公式（15）求解不含循环噪声成份的x（tk）和v（tk），以公式（24）计算出不含反馈噪声成份的过程输出yc（ tk），以yc（tk）和v（tk）的预滤波数据建立过程向量：

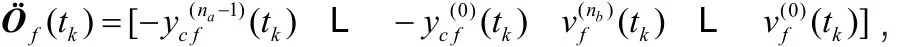
辅助向量：

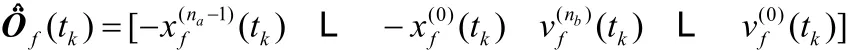
由x（tk）和v（tk）的预滤波数据建立，以公式（18）实现混合Box-Jenkins模型的过程参数辨识。算法的过程描述如下：

2）设定初始循环j=1和最大循环次数Itrmax

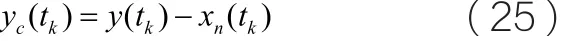
4）使用预滤波器f （i ）=pi/A（p）计算连续预滤波变量值

c

5）计算有色噪声ξ（tk）=y（tk）-x（tk），使用IVARMA算法辨识噪声模型Gn，令fd=1/Gn，根据和计算预滤波变量值和

4 改进算法的仿真测试

为了验证算法的有效性，首先对算法进行仿真验证，给定过程传递函数模型如公式（26）所示：

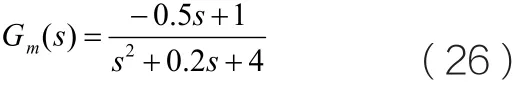
选择如下的PI控制器：

干扰模型为一阶模型，公式如下：

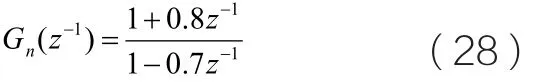
仿真使用的设定值幅值为±1， 分段连续的激励信号， 系统响应数据应用零阶保持器，以采样间隔为的速率获取，数据量取N=3000。应用Monte Carlo Simulation（MCS） 分析方法随机产生100组高斯白噪声，通过调整高斯白噪声的方差，产生设定值与有色噪声的信噪比为10dB的有色噪声信号。

为了验证算法的寻优效果，应用同样的闭环输入输出，分别使用中CONSTID工具箱中CLRIVC算法，MATLAB的系统辨识工具箱中的PEM连续B-J模型计算方法和DNIV算法进行仿真。三种算法的100组MSC仿真结果见表1。表中列了三种方法的100组数据计算结果均值，结果标准差和平均绝对误差和MAE 。MAE 定义为：

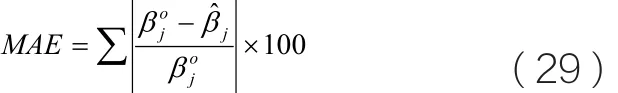
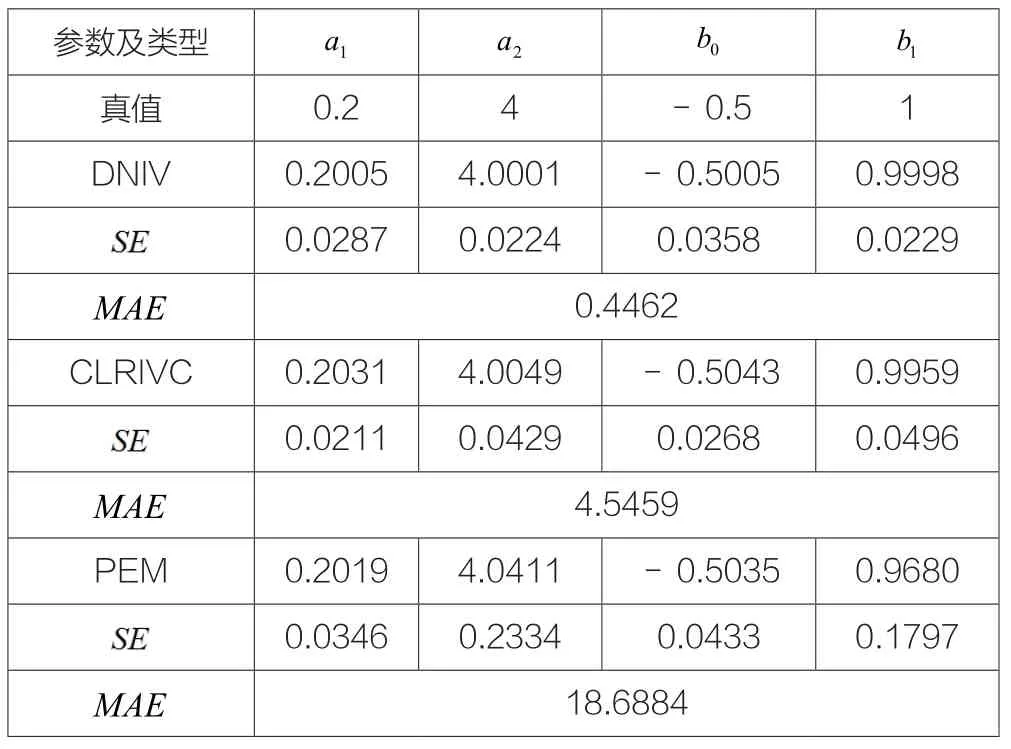
表1 三种算法的MSC仿真结果表

从表中的结果可以看出尽管CLRIVC算法中的部分参数的标准差略优于DNIV算法，但DNIV的参数均值和MAE均优于CLRIVC的计算结果，而PEM算法虽然能得到较好的结果，相对于DNIV和CLRIVC来说，效果较差。

结论

在装置正常生产条件，针对闭环控制回路，过程的输入输出数据存在一定的相关性，传统的开环辨识算法结果不理想问题提出了连续时间闭环混合Box-Jenkins模型辨识方法，为提高噪声模型的辨识精度，提出了带有惩罚因子的极大似然参数估计算法。DNIV算法首先基于最小二乘状态变量滤波获取初步的过程模型参数，然后剔除回路数据中的循环干扰成份，以辅助变量算法进行混合Box-Jenkins模型辨识，从而获取更精确的过程模型参数。仿真实验证明了算法的有效性。

10.3969/j.issn.1001- 8972.2016.19.036