变化多端的全等三角形

万广磊

变化多端的全等三角形

万广磊

全等三角形的魅力在于运动.中考数学试题一般以平移、轴对称（翻折）和旋转为图形变换方式，综合考查全等三角形的判定与性质.下面以2016年的中考数学题为例进行剖析.

一、平移

例1（2016·湖北武汉）如图1，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE.

图1

【分析】本题考查了全等三角形的判定与性质，解题的关键是根据已知条件结合图形选择合适的方法.要证AB∥DE，需证∠ABC=∠DEF，因此考虑证明它们所在的两个三角形全等.已知有两组边分别相等，再证明另一组边分别相等，利用“SSS”证明即可.具体步骤：

证明：∵BE=CF，∴BC=EF；

在△ABC和△DEF中，

∵BC=EF，AB=DE，AC=DF，

∴△ABC≌△DEF（SSS），

∴∠ABC=∠DEF，∴AB∥DE.

【点评】纵观本题，图中的△DEF与△ABC是通过平移得到的，平移不改变图形的形状和大小，平移前后对应线段相等且平行（或在同一直线上）.在有两组对应边分别相等的前提下，可以求第三组对应边相等，或者求两组对应边的夹角相等，注意必须是夹角；若有三组对应边分别相等，则可以直接根据“SSS”求解.已知两边和其中一边的对角分别相等，不能判定三角形全等，即不存在“SSA”判定三角形全等的方法.如图2所示，AB=DE，∠B=∠DEF，AC=DF，但是△ABC与△DEF不全等.

图2

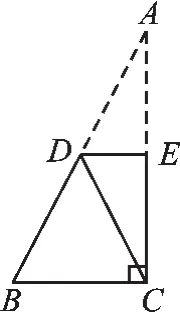
图3

二、轴对称（翻折）

例2（2016·江西）如图3，在Rt△ABC中，∠ACB=90°，将Rt△ABC向下翻折，使点A与点C重合，折痕为DE，求证：DE∥BC.

【分析】本题考查了三角形的折叠和平行线的判定，解题的关键是运用轴对称图形的性质.要证明DE∥BC，必须考虑到∠AED=∠ACB= 90°，而如何得到∠AED=90°，就联想到ED平分一个平角，这可以由折叠得到.

证明：由折叠可知：△ADE≌△CDE，

∴∠AED=∠CED，

又∵点A与点C重合，∴∠AEC为平角，

∴∠AED=∠CED=90°，

∵∠ACB=90°，

∴∠AED=∠ACB，∴DE∥BC.

【点评】图中的△ADE与△CDE是通过折叠得到的，折叠属于轴对称变换，根据轴对称图形的性质，折叠前后图形的形状和大小不变，进而可以找出位置变化前后相应的角相等，线段相等，进而转化为全等判定的条件.

三、旋转

例3（2016·湖北荆门）如图4，在Rt△ABC中，∠ACB=90°，点D、E分别在AB、AC上，CE= BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF.

（1）补充完成图形；

（2）若EF∥CD，求证：∠BDC=90°.

图4

图5

【分析】本题是一道作图与证明的综合题，其中涉及直角三角形、图形的旋转、全等三角形的判定、平行线的性质等，在解第（2）问时，关键是得到△BCD≌△ECF，结合条件推出∠F=90°，通过全等三角形对应角相等，得到∠CFE=∠BDC=90°.具体步骤：

解：（1）解：所补图形，如图5所示；

（2）证明：∵∠BCA=∠DCF=90°，

∴∠BCA－∠DCA=∠DCF－∠DCA，

即∠BCD=∠ECF.又CB=CE，CD=CF，

∴△BCD≌△ECF（SAS），∴∠BDC=∠CFE，

∵CD∥EF，∴∠DCF+∠CFE=180°，

∵∠DCF=90°，∴∠BDC=∠CFE=90°.

【点评】图中的△CEF是通过旋转△CBD得到的，旋转不改变图形形状和大小，旋转角相等，由此可以得到相应的角相等，为全等三角形的判定和角度的计算提供了条件.

四、旋转与平移的组合

例4（2016·河北）如图6，点B、F、C、E在直线l上（F、C之间不能直接测量），点A、D在l异侧，测得AB=DE，AC=DF，BF=EC.

（1）求证：△ABC≌△DEF；

（2）指出图中所有平行的线段，并说明理由.

图6

【分析】本题考查了全等三角形的判定与性质，关键是寻找全等三角形判定的条件.第（1）问中，已知两边分别相等，再根据BF=EC得BC=EF，可根据“SSS”证得△ABC≌△DEF；（2）由△ABC≌△DEF可得∠ABC=∠DEF，∠ACB=∠DFE，再根据“内错角相等两直线平行”可证得AB∥DE，AC∥DF.具体步骤：

解：（1）证明：∵BF=EC，∴BF+FC=EC+CF，

即BC=EF；又∵AB=DE，AC=DF，

∴△ABC≌△DEF.

（2）有AB∥DE，AC∥DF.

理由：∵△ABC≌△DEF，

∴∠ABC=∠DEF，∠ACB=∠DFE.

∴AB∥DE，AC∥DF.

【点评】图中的△DEF与△ABC是通过旋转再平移得到的，其中的对应边和对应角并不会因为位置的变化而改变，这也为全等三角形和平行线的判定提供了条件.

（作者单位：江苏省扬州大学附属中学东部分校）