用好例题拓展提高学习实效

尹平

用好例题拓展提高学习实效

尹平

教科书中的例题是围绕本节（或本章）的概念、定理而设置的典型题目，在平时的学习过程中，往往有些同学不重视、不关注.本文借助于课本中一道题，加以变式拓展，希望能带给同学们一些新的认识.

原题呈现：苏科版《数学》九年级上册第34页：

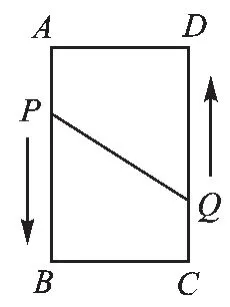
图1

如图1，在矩形ABCD中，AB= 16cm，BC=6cm，点P从点A出发，以3cm/s的速度向点B移动，直到到达点B为止；同时点Q从点C出发，以2cm/s的速度向点D移动，经过多长时间P、Q两点之间的距离是10cm？

【分析】设运动时间为t秒，因为PQ长为10cm，所以构造出以PQ为斜边的直角三角形，作PH⊥CD，垂足为H，用t表示出线段HQ的长，用勾股定理列方程即可求解.

解：设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，

图2

如图2，作PH⊥CD，垂足为H，

则PH=BC=6，PQ=10，

HQ=CD-AP-CQ=16-5t.

因为PH2+HQ2=PQ2，

可得：（16-5t）2+62=102，

解得t1=4.8，t2=1.6.

答：P，Q两点从出发经过1.6或4.8秒时，点P，Q间的距离是10cm.

变式一条件不变，在运动过程中，点P和点Q之间的距离可能是18cm吗？如果可能，求出运动时间t，如果不可能，请说明理由.

解：与上述过程相同，

（16-5t）2+62=182，

所以在运动过程中，点P和点Q之间的距离不可能是18cm.

变式二（2016·威海一模）如图3，在矩形ABCD中，AB=16cm，BC=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，直到到达点B为止，点Q以2cm/s的速度向点B移动，经过多长时间P、Q两点之间的距离是10cm？

图3

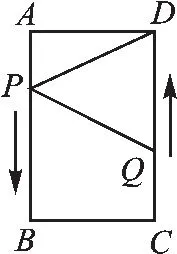
图4

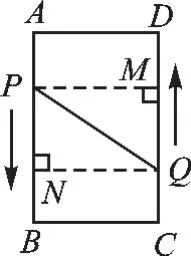
图5

【分析】设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，表示出PB、BQ，利用勾股定理建立方程求得答案即可.

解：设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，

则PB=16-3t，BQ=6-2t，

因为PB2+BQ2=PQ2，

所以（16-3t）2+（6-2t）2=102，

变式三条件不变，如图4，∠DQP能否为直角？若能，请求出相应的时间t的值.

【分析】题目明确问∠DQP能否为直角，所以需要构建△DQP，再根据勾股定理求解.

解：能.

由∠DQP=90°，则有DQ2=DP2-PQ2，

所以（16-2t）2=62+（3t）2-62，

时，∠DQP为直角.

变式四条件不变，经过多长时间，点P、Q、D组成的三角形是等腰三角形？

【分析】设时间为ts，过P作PM⊥CD于M，过Q作QN⊥AB于N，根据四边形ABCD是矩形可知DC=AB=16cm，AD=BC=PM=QN=6cm，∠A=∠C=∠B=∠ADC=90°，故DM=AP=3tcm，BN= CQ=2tcm，再分DP=PQ，DQ=PQ及DP=DQ三种情况进行讨论即可.

解：设时间为ts，过P作PM⊥CD于M，过Q作QN⊥AB于N（如图5），

因为四边形ABCD是矩形，所以DC=AB= 16cm，AD=BC=PM=QN=6cm，

∠A=∠C=∠B=∠ADC=90°，

则DM=AP=3tcm，BN=CQ=2tcm.

分为三种情况：

①当DP=PQ时，则DM=MQ=3tcm，

∵3t+3t+2t=16，解得：t=2；

②当DQ=PQ时，在Rt△PNQ中，由勾股定理得：（16-2t）2=62+（16-3t-2t）2，

7t2-32t+12=0，

解得：

③当DP=DQ时，在Rt△DAP中，由勾股定理得：（16-2t）2=62+（3t）2，

即5t2+64t-220=0，

图6

变式五如图6，在矩形ABCD中，AB= 12cm，BC=4cm，点P以4cm/s的速度从顶点A出发沿折线A—B—C向点C运动，同时点Q以2cm/s的速度从顶点C出发向点D运动，当其中一个动点到达末端停止运动时，另一点也停止运动.问两动点经过多长时间，使得点P与点Q之间的距离为

【分析】注意题目中对两动点运动的表述，从而知道每个动点的运动路径.不难看出P分别在AB、BC上运动，所以需要分类讨论.

①当0＜t≤3时，则有（12-4t-2t）2+42=20，

②当3＜t≤4时，则有（16-4t）2+（2t）2=20，

得方程5t2-32t+59=0，

此时Δ＜0，此方程无解.

通过以上题目的变式，同学们一定会发现解决此类问题，关键是要会表示出相关线段长，利用勾股定理，再结合方程进行求解.同学们也可以作适当的变式，试试看，你会发现新天地.

（作者单位：江苏省海门市正余初级中学）