基于模糊理论与数据融合的电厂故障诊断技术

代宪亚，茅大钧

(上海电力学院 自动化工程学院, 上海 200090)



基于模糊理论与数据融合的电厂故障诊断技术

代宪亚，茅大钧

(上海电力学院 自动化工程学院, 上海 200090)

电厂作为一个复杂的、对安全性能要求非常高的系统，准确地对其进行故障诊断非常有必要。将模糊算法、神经网络与DS证据理论进行合理高效地结合，给出了一种新的故障诊断方法。从隶属度函数确定、征兆参数模糊化处理、神经网络诊断，到最终使用DS证据理论进行数据融合，给出了完整的诊断结构流程图，并运用MATLAB软件进行GUI设计，直观地显示诊断结果。仿真实验结果证明了该方法的准确性与可行性。

故障诊断; 模糊理论; 神经网络; DS证据理论

随着故障诊断技术的发展，其要求愈发地趋向于高效率、安全性、可靠性，诊断方法的复杂性也越来越高。电厂是一个复杂的、对安全性能要求非常高的系统，更有必要进行准确高效的故障诊断。

快速、准确地做出故障判断并给出对应的专家意见，有助于对故障进行快速修复，从而使损失降到最小。目前，较为常见的故障诊断方法有专家系统、神经网络、模糊逻辑、数据融合等，各自都有其优、缺点[1-3]。对于电厂而言，考虑到其运行的复杂性，单纯的一种方法并不能做出准确的故障判断，错误的诊断将影响电厂的故障修复，甚至产生更严重的后果，带来更大的损失[4-6]。如文献[3]中只采用模糊神经网络进行故障诊断，而文献[7]中只研究了证据理论融合，若单纯地进行多次诊断，则其方法之间的关联性不强，增加了诊断时间。本文根据电厂特性，将数据进行分组，并选择合适的隶属度函数，对特征参数进行模糊化处理，将处理结果作为神经网络的诊断输入，最终由DS证据理论将多个神经网络的诊断结果合理地融合在一起，得出最终的故障发生概率。该方法诊断迅速，不需要分步诊断，并通过模糊处理使得诊断结果更加准确。

1　故障诊断模型建立

1.1模糊化处理

确定性体现的是非此即彼、界限明确的思想，但随着系统复杂度的增加，系统特性的精确度就会下降，即出现亦此亦彼、界限模糊的现象，这种现象体现的就是模糊性概念。电厂具有高度复杂性，征兆参数与故障之间并不具有十分明确和直接的关联。因此，模糊理论适用于电厂的故障诊断。

在经典集合理论中，元素x和集合M之间的关系为属于和不属于，故x的隶属度函数为

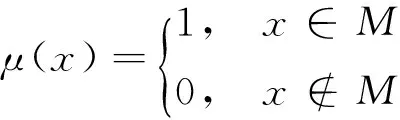
(1)

而在模糊理论中，元素与集合的关系不再这么明确，而变得界限模糊，用函数表示为

μm(x)→[0，1]，x∈U

(2)

即隶属度不再只是0和1，而是[0，1]整个区间，体现的是x对M的隶属程度，μm(x)靠近1的程度就是x从属于M的程度[1-2]。

当电厂运行不正常时，一定存在着某些参数不在正常范围内，即存在偏大或偏小的可能。运用模糊思想进行处理，通过隶属度函数可以从这些征兆参数中提取其偏大、正常、偏小的可能性程度。

1.2隶属度函数的确定

根据文献[1、3]中关于隶属度函数选取原则的详细阐述，本文方法选取高斯和Sigmoid两种函数。前者作为“正常”的隶属度函数，后者作为“偏大”与“偏小”的隶属度函数，分别对征兆参数进行模糊化处理。

偏小的隶属度函数为

Pl=1-[1+e-a(d-l)]-1

(3)

正常的隶属度函数为

Pk=e-b(d-k)2

(4)

偏大的隶属度函数为

Ph=[1+e-c(d-h)]-1

(5)

式中，d为征兆参数；a、b、c、l、k、h均为常数。根据文献[1、3]中的隶属度函数选取原则以及高斯与Sigmoid函数的特性曲线，当d偏小的程度越大，则式(3)越趋向于1，其他两个函数越趋向于0；当d偏大的程度越大，则式(4)越趋向于1；当d越是正常，则式(5)越趋向于1；且对同一征兆参数而言，只允许有一个最大隶属度。

当电厂正常运行时，每个测量参数都有一个正常范围。设某一征兆参数d的正常范围为[ds，dq]，即ds和dq分别为该参数正常范围内的最小值和最大值，取区间中心值为do。为求得其中的常量，先保留1/15的划分裕度，重新划分参数界限，则正常输入下限值为

(6)

正常输入中心值为

(7)

正常输入上限值为

(8)

将此征兆参数的(ds，0.5)、(L，0.4)代入式(3)；将点(L，0.5)、(do，1)代入式(4)；将点(H，0.4)、(dq，0.5)代入式(5)，可求出常数a、b、c、l、k、h。

以左环路主蒸汽辐射剂量(mSv)为征兆参数d举例，其正常范围为[144，160]，则 ds=144，dq=160，do=152。根据式(6)～(8)求出L=145.067，N=152，H=158.93。将(144，0.5)、(145.067，0.4)代入式(3)；将点(145.067，0.5)、(152，1)代入式(4)；将点(158.93，0.4)、(160，0.5)代入式(5)，求得常数a=0.38，b=0.0144，c=0.38，l=144，k=152，h=160，则得到

Pl=1-[1+e-0.38(d-144)]-1

(9)

Pk=e-0.014 4(d-152)2

(10)

Ph=[1+e-0.38(d-160)]-1

(11)

则得到以左环路主蒸汽辐射剂量(mSv)为征兆参数d的隶属度函数如图1所示。由图可见，结果满足隶属度函数的选取原则。

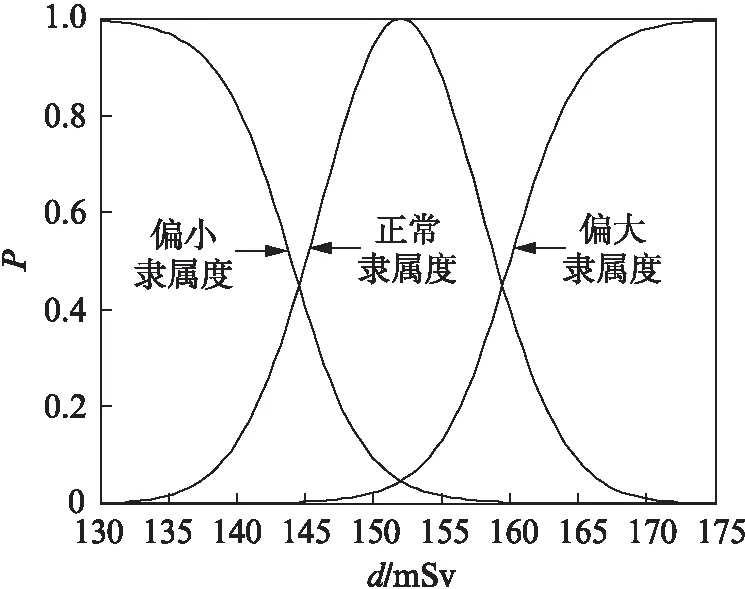
图1　参数d的隶属度函数图Fig.1　Membership function of parameter d

1.3模糊神经网络建立

采集到的征兆参数经各自对应的隶属度函数模糊化处理后，可得到3个隶属度值，如d1模糊化处理后得到P1l、P1k和P1h，以此类推。将结果作为神经网络的输入层，各故障发生的概率作为神经网络的输出层，建立模糊神经网络模型，如图2所示。

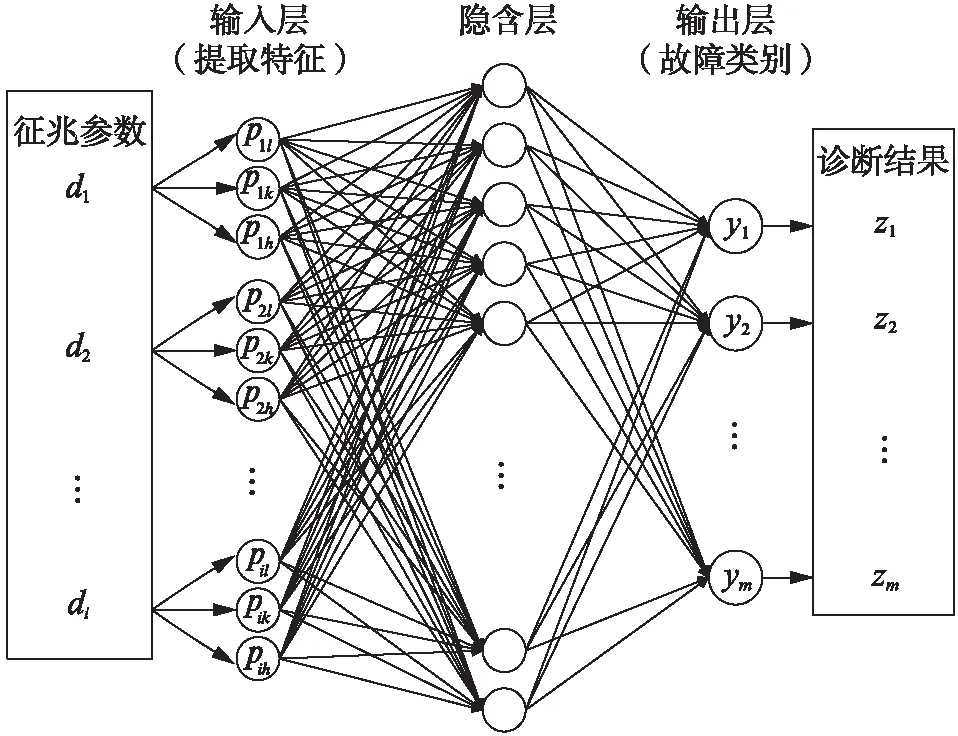
图2　模糊神经网络模型Fig.2　Fuzzy neuron network model

电厂运行时，需要监测的数据很多，每一种故障都具有很多故障征兆参数，若将所有征兆参数只用一个神经网络进行诊断，则经模糊化处理后的结果将会出现3倍的数据量，必然使得诊断网络输入节点较多、诊断时间过长。因此，需要将征兆参数进行归类分组，将诊断网络也分解成n个子网络，分别对分组后的征兆参数运用神经网络进行故障诊断，然后将各子网络的诊断结果进行数据融合，得到最终结果[7]。

调用神经网络进行诊断前，先要对其进行网络训练[8]。将电厂原有的历史故障数据作为样本，并归类分组、提取特征值。对于网络训练的输出样本，发生的故障类型特征值取为1，其他故障类型和正常状态的特征值取为0；若未发生故障，则正常状态的特征值取为1，其他故障类型为0，之后，进行神经网络训练，并保存网络以备调用[9-10]。假设共分为n个子神经网络，有(m-1)种故障，加上1种正常状态，则有m种诊断结果。训练样本的征兆参数提取特征值的方法如下：① 若征兆参数大于最大正常值，则偏大隶属度取为1，其他隶属度都取为0；② 若征兆参数小于最小正常值，则偏小隶属度取为1，其他隶属度都取为0；③ 若征兆参数介于最大与最小正常值之间，则正常隶属度取1，其他隶属度都取为0。

1.4数据融合

数据融合是将多源数据经过有效分析处理后，融合成一组结果。本文采用DS证据理论数据处理方法，将根据不同种类参数进行诊断的结果数据融合[11-13]。设采用n个子神经网络进行故障诊断，会得到n组诊断结果，利用DS证据理论对n组结果进行处理，得到故障发生概率值。

每个神经网络的诊断结果是一组数据，每一组诊断结果都包含m个状态发生的可能性，为使最终结果为故障概率值(即0～1)，故要先将这些数据进行归一化处理，即

(12)

将归一化后的n组数据进行DS证据理论融合，先在两组数据之间进行融合，再将结果与第3组数据融合，依次类推，直到将所有数据融合完毕，得出最后结果。设两组需要融合的数组为 x={x1，x2，…，xt}(r=1,2,…,t)，y={y1，y2，…，yt}(j=1,2,…,t)，融合后的数组为z={z1，z2，…，zt}，则有

(13)

综上所述，故障诊断结构流程如图3所示。

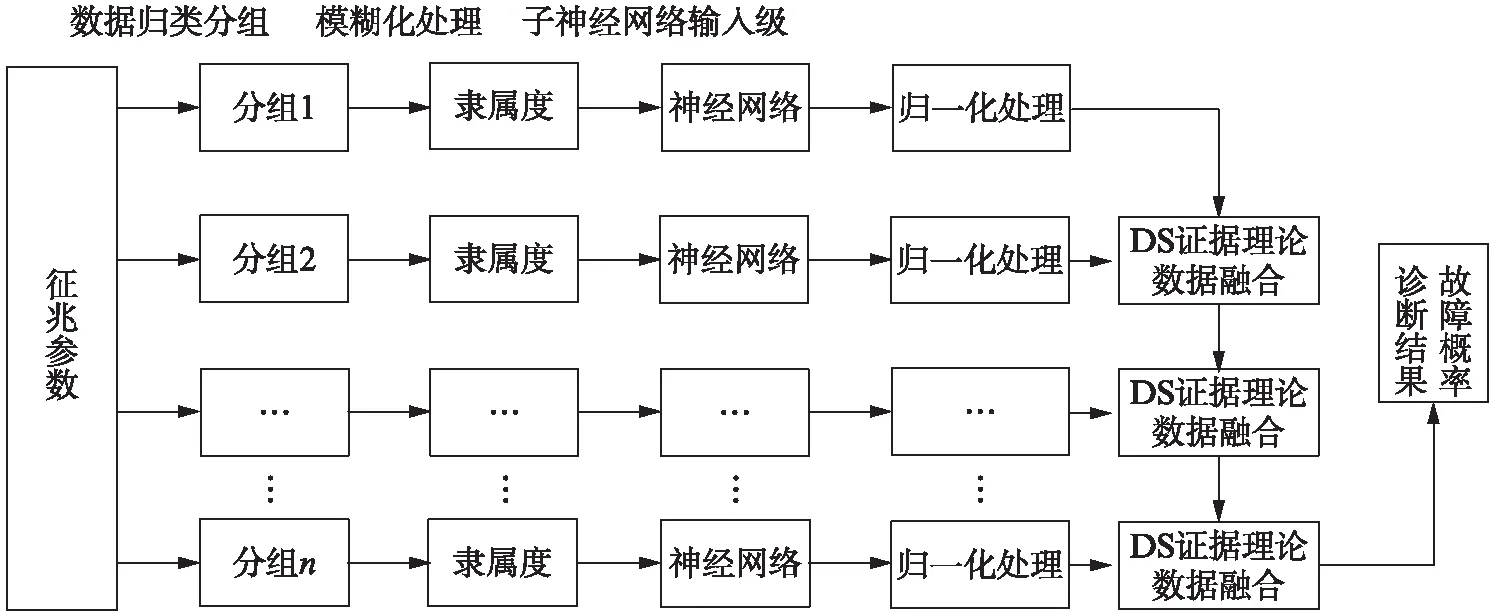
图3　故障诊断结构流程图Fig.3　Flow chart of fault diagnosis

2　GUI界面设计与仿真实验

文献[7]中给出了秦山核电厂仿真机关于主冷却系统的故障仿真数据，本文以此作为参考数据，运用MATLAB软件进行图形用户界面(Graphical User Interface, GUI)设计[14-15]与故障诊断仿真。

本文设计的GUI诊断界面如图4所示。由图可见，该诊断界面包括数据采集与显示、神经网络训练、诊断结果显示和专家建议4个部分。

仿真实验时，根据数据类型，将征兆参数归类，并分为3组，由3个子神经网络进行故障诊断。在故障诊断前，先点击按钮“神经网络1训练”、“神经网络2训练”、“神经网络3训练”分别对每个神经网络进行训练，并保存网络以备调用；然后，点击“数据采集”按钮，实现征兆参数由数据库到GUI界面的传递，完成模糊处理；最后，点击“开始诊断”按钮，将模糊处理后的隶属度分别调用到已保存的神经网络进行故障诊断，最后将

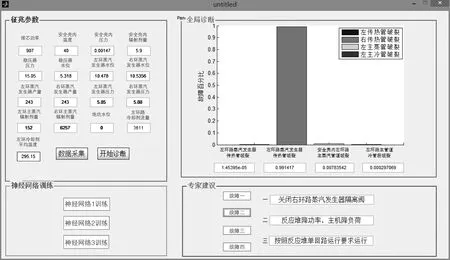
图4　诊断界面及仿真诊断结果Fig.4　Interface of fault diagnosis and the diagnosis results

3个神经网络的诊断结果进行数据融合，得到最终故障发生的概率值，由柱状图显示出来，并显示具体的概率值。根据诊断结果，可选择对应的专家建议，对故障进行正确、及时处理。

以右环路蒸汽发生器传热管破裂故障为例进行仿真实验(以下征兆参数均由秦山核电厂仿真机提供)。各征兆参数的正常范围如表1所示。

先由仿真机提供每种故障类型和正常状态时的各组数据，将数据归类分组，依照神经网络训练方法进行网络训练。然后，由参数正常范围界限求出各自的隶属度函数。根据式(6)～(8)可求得隶属度函数常数参量结果，如表2所示。

仿真机提供该故障的征兆参数如下：d1=907; d2=40; d3=0.00147; d4=5.9; d5=15.05; d6=5.318; d7=10.478; d8=10.5356; d9=243; d10=243; d11=5.85; d12=5.85; d13=152; d14=6257; d15=0; d16=3611; d17=295.15。诊断结果见图4。由诊断结果可见，该故障发生的概率明显高于其他故障，针对该故障选择专家建议，及时作出处理。

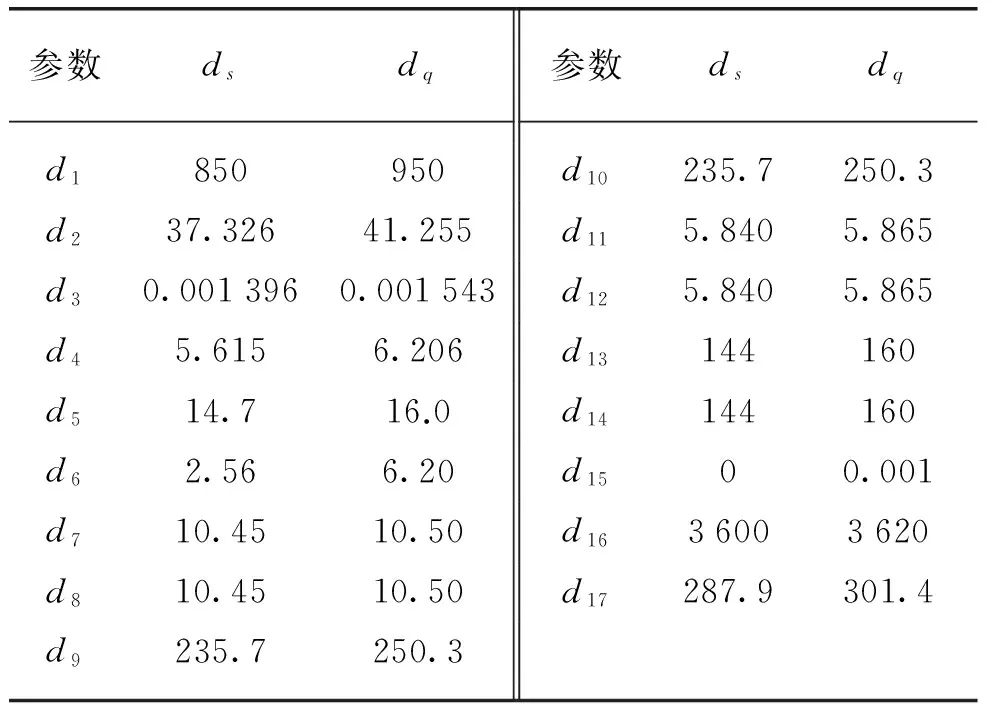
表1　各参数正常范围

注：d1为堆芯功率，MW；d2为安全壳内温度，℃；d3为安全壳内压力，MPa；d4为安全壳内辐射剂量，mSv；d5为稳压器压力，MPa；d6为稳压器水位，m；d7为左环路蒸汽发生器水位，m；d8为右环路蒸汽发生器水位，m；d9为左环路蒸汽发生器蒸汽产量，kg/s；d10为右环路蒸汽发生器蒸汽产量，kg/s；d11为左环路蒸汽发生器压力，MPa；d12为右环路蒸汽发生器压力，MPa；d13为左环路主蒸汽辐射剂量，mSv；d14为右环路主蒸汽辐射剂量，mSv；d15为地坑水位，m；d16为左环路冷却剂流量，t/h；d17为左环路冷却剂平均温度，℃

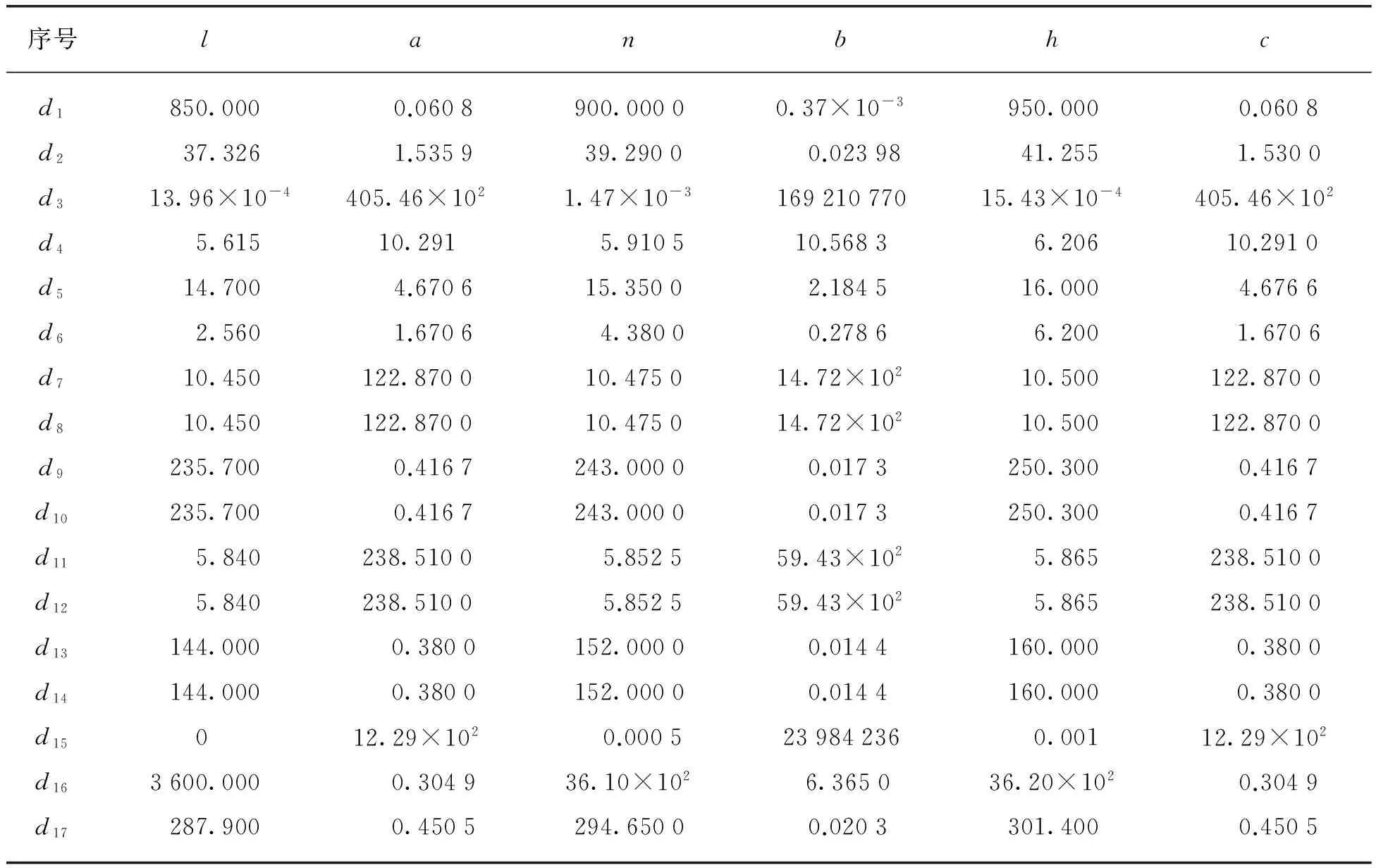
表2　各参数隶属度函数常数参量

3　结　语

针对电厂运行的复杂性，本文提出基于模糊理论与数据融合的电厂故障诊断方法。详细介绍了模糊理论与DS证据理论在诊断中的应用，将模糊理论、神经网络与DS证据理论合理高效地结合，提高诊断结果的准确性。从隶属度函数确定、征兆参数模糊化处理、神经网络诊断，到最终DS证据理论进行数据融合，文中给出了完整的诊断结构流程图。最后运用MATLAB完成GUI界面设计与仿真。仿真结果证明了该方法的准确性与可行性，对电厂故障诊断的研究具有一定意义。

[1]戴利雄.基于模糊神经网络的智能故障诊断技术研究[D].大连：大连海事大学，2009：28-29.

[2]张洪瑾.基于模糊神经网络的掘进机液压系统故障诊断研究[D].南京：南京理工大学，2013：29.

[3]常继彬.基于模糊神经网络的中央空调智能故障诊断研究[D].重庆：重庆大学，2007：26-44.

[4]杨静，王玉海，郭凡.故障诊断在电厂热工系统中的应用研究[J].科技资讯，2012(15)：118.

[5]李红卫，杨东升，孙一兰，等.智能故障诊断技术研究综述与展望[J].计算机工程与设计，2013，34(2)：632-637.

[6]徐青，黄昕，刘海力.垃圾焚烧电厂烟气脱硝技术的模糊综合评价[J].热力发电，2012，41(7)：37-40，48.

[7]董雅欣.核电厂主冷却剂系统分布式故障诊断技术研究[D].哈尔滨：哈尔滨工程大学，2012：41-43.

[8]梁毅超.基于Matlab的某电厂汽轮机振动故障诊断系统的研究[J].通用机械，2014(5)：70-72.

[9]陈丹江，叶银忠.基于多神经网络的三电平逆变器器件开路故障诊断方法[J].电工技术学报，2013，28(6)：120-126.

[10]公茂法，张言攀，柳岩妮，等.基于BP网络算法优化模糊Petri网的电力变压器故障诊断[J].电力系统保护与控制，2015(3)：113-117.

[11]廖瑞金，孟繁津，周年荣，等.基于集对分析和证据理论融合的变压器内绝缘状态评估方法[J].高电压技术，2014，40(2)：474-481.

[12]韩德强，杨艺，韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策，2014，29(1)：1-11.

[13]李平，黄国樑，彭道刚，等.基于神经网络和D-S证据的电厂凝汽器故障诊断研究[J].华东电力，2014，42(6)：1227-1232.

[14]吴宏岐，周妮娜，王春英.基于RBF神经网络的变压器故障诊断及MATLAB仿真研究[J].科学技术与工程，2010，10(5)：1249-1251，1275.

[15]杨邵伟，韩天，尹忠俊，等.MATLAB GUI界面设计在电机故障诊断中的应用[J].机电产品开发与创新，2007，20(6)：118-122.

Fault Diagnosis for Power Plant Based on Fuzzy Theory and Data Fusion

DAI Xianya，MAO Dajun

(College of Automation Engineering， Shanghai University of Electric Power, Shanghai 200090, China)

As a complicated system with strict safety constraints, a power plant requires accurate fault diagnosis.The fuzzy theory, neural network and DS evidential theory are combined to form a new fault diagnosis method.In this paper, a complete flow chart of fault diagnosis is presented, including choice of membership function, fuzzy processing of symptom parameters, modeling of the neural network diagnosis, and data fusion with the DS evidence theory.MATLAB is used to design GUI to visually display the results.Simulation results show that the method is accurate and feasible.

fault diagnosis; fuzzy theory; neural network; DS evidential theory

2016-04-29

代宪亚(1992-)，男，硕士生，主要研究方向为电气系统检测与故障诊断，E-mail：dxy05162012@126.com

2095-0020(2016)04-0201-06

TM 76;TM 744

A