温度对T700/3234反对称铺设圆柱壳结构的双稳态特性影响

张　征，　潘　豪，　叶钢飞，　李　琛，2，　吴化平，　柴国钟

(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室， 杭州 310032； 2.中国计量大学 质量与安全工程学院，杭州 310018)



温度对T700/3234反对称铺设圆柱壳结构的双稳态特性影响

张征1，潘豪1，叶钢飞1，李琛1，2，吴化平1，柴国钟1

(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室， 杭州 310032； 2.中国计量大学 质量与安全工程学院，杭州 310018)

讨论温度对T700/3234反对称铺设圆柱壳结构的双稳态特性的影响。通过热压固化成型工艺制备了三种不同铺层层数的试样，采用两点加载的方式，使用在现有的拉伸试验机上改装的实验测试平台驱动反对称铺设圆柱壳结构进行稳态转变，持续捕捉实验过程中的数据，得到在20℃，40℃，60℃和80℃温度下的载荷—位移曲线的变化规律及稳态转变载荷。实验后，通过图像处理技术得到曲率和扭曲率等数据。系统分析稳态转变载荷和稳态曲率变化情况，并对存放时间对壳结构的影响进行了讨论。结果表明，温度对双稳态结构稳态转变影响较大，给出了温度对snap-through和snap-back过程的影响规律。

碳纤维复合材料；反对称层合壳；双稳态特性；温度场

具有反对称铺设(铺层方式如：[+α/-α/+α/-α]等)的碳纤维复合圆柱壳结构有两种稳态结构[1]，即在一个稳定的圆柱壳结构上，外界对其施加一定的外在驱动力(例如机械载荷)，可以使其转变为另一种稳定的结构，并且这种结构不需要外力维持。这种具有双稳态特性的结构在可变形结构上(如可变形机翼、风力发电机叶片等)有较大的应用前景。碳纤维结构在实际应用过程中受周围环境(如温度、湿度等)影响较大[2-3]，因此本研究采用不同的实验环境，模拟不同试件在不同温度下的力学行为变化，对揭示在温度场影响下的双稳态壳结构变形特性具有重要意义。

近年来，国内外越来越多的学者开始关注双稳态复合圆柱壳结构的双稳态性能[4-6]，此种结构具有两种稳定结构状态，具有承载能力高、空间利用率好以及结构轻便等优点。反对称铺设的双稳态复合圆柱壳作为其中的一种结构，很多学者研究其形变状况、实现稳态转变的驱动方式以及在结构方面的应用[7,8]。Zhang等[9,10]对反对称铺设的圆柱壳结构的双稳态性能进行了理论推导、有限元模拟以及实验，得到了圆柱壳不同几何尺寸以及铺层方式对双稳态性能的影响情况。双稳态复合圆柱壳结构多由碳纤维复合材料制备而成，温度、湿度等因素对碳纤维复合材料性能具有重要的影响。Tsai等[11]通过实验方法来研究非对称铺设复合材料结构在潮湿环境中敏感性的影响，得到了吸湿比重、高度、曲率半径等因素与时间的变化关系。Youssef等[12]通过模拟航空航天环境，研究了湿度、温度及湿热耦合作用下碳纤维复合材料的疲劳损伤问题。Moore等[13,14]利用数值模拟方法，得到非对称铺设双稳态复合材料层合板在高温固化过程中，层合板各点位移随温度变化之间的关系，并且通过实验，获取了非对称铺设双稳态复合材料层合板由高温冷却至室温时不同温度下的形状。Eckstein等[15]利用ABAQUS有限元软件，考虑了材料参数随温度变化的特性，模拟了非对称铺设层合板高温固化过程中温度与曲率之间的关系。

非对称正交铺设层合板的两种稳态结构曲率方向相反，而反对称层合圆柱壳的两种稳态结构曲率方向相同。此外，反对称层合圆柱壳在铺设角和整体尺寸结构的改变上比非对称正交铺设层合板具有更好的设计性。大部分学者都关注湿热因素对正交铺设的双稳态层合板高温固化过程的影响，只有少部分学者着眼于研究温度对反对称铺设的双稳态复合圆柱壳结构的双稳态性能的影响。反对称铺设的双稳态复合圆柱壳结构作为一种新型的可延展性结构一般应用于环境复杂多变工况，研究温度因素对双稳态复合材料结构的影响对其应用有着重要理论意义。通过温度影响下的双稳态实验，可以获取不同温度影响下反对称复合圆柱壳的不同形变情况，并且利用机械加载的方式，得到其两个稳态转变过程所需载荷随温度变化而变化的情况。通过实验研究温度对反对称铺设的双稳态复合圆柱壳影响情况，可以为其在可变形结构上的应用提供有效的预测和保证。

1　实验试样和测试平台

反对称层合板圆柱壳试样采用由多个厚度为0.185 mm的碳纤维填充环氧树脂(T700/3234)单层板按照所设计的尺寸剪裁，然后按照一定的铺设方式在半圆柱形钢制模具中高温保压固化并脱模后制得。在初始半径和铺层数一定的情况下，反对称圆柱壳的第二稳态卷曲半径随着铺设角的增大先减小而后又逐渐增加[17]。在初步设计初始截面半径R1=25 mm的情况下，使用铺设角为45°的反对称圆柱壳存在比其他铺设角更小的第二稳态卷曲半径，相比其他铺设角度更易于研究温度对反对称圆柱壳的影响。设计制备的反对称圆柱壳结构的如表1所示，几何参数设定如下：反对称圆柱壳长度L=100 mm、圆心角β=180°、初始截面半径R1=25 mm，每层厚度t=0.185 mm,分别为4层，5层和6层的试样。

在此，标记4层的反对称圆柱壳为试样1，5层的反对称圆柱壳为试样2，6层的反对称圆柱壳为试样3，具体实物照片如图1所示。由于试样制备的误差会对圆柱壳初始扭曲率kxy1造成影响，测试得到试样1,2和3的两直边的初始扭曲率分别为1.2757 m-1，0.5163 m-1和1.3929 m-1。

表1　反对称圆柱壳结构试样

图1　实验制备的试件Fig.1　Manufactured specimens

使用含温控箱的REGER 3010型电子万能材料试验机对试样进行加载，其标配的力传感器量程为1 kN，误差0.5%～1%左右，并在此基础上进行了装夹和加载部分的改装。该实验平台改装部分主要由压头和夹具组成。压头采用半径为5 mm，圆心角为160°的圆形压头。夹具是由两个滑块和一个夹具底座装配而成，其中夹具底座基本尺寸为150 mm×100 mm，照片如图2所示。

实验总共进行5次，前3次进行不同铺层层数下的稳态转变实验，后2次进行试样1和试样2在一定时间间隔下重复的2次实验，以讨论存放时间对双稳态结构性能的影响。具体操作流程为：将选定试样放置在夹具上，确保压头正好加载在反对称圆柱壳的两直边的中点处，压头的最低点尽可能靠近两直边，但不接触，如图2(b)所示。运行控制加载程序，使压头以一定的进给速率进行位移加载，使反对称圆柱壳进行稳态转变，压头向下加载到一定距离时，反对称圆柱壳发生突变，两直边变为圆弧边，而之前的圆弧边转变为直边。此实验过程称为Snap-through过程，并把此过程的逆过程称为Snap-back过程。图3中试样1,2,3的左侧图为Snap-through过程的载荷位移曲线，试样1,2,3的右侧图为Snap-back过程的载荷位移曲线。为了观察试样两直边的扭转情况和圆弧边的曲率变化情况，对该试样拍摄Snap-through和Snap-back过程的转变前后的两直边和圆弧边的照片，通过采用Matlab编程和照片处理软件coredraw相结合的自主研发软件对实验照片进行处理，可以得到两直边的扭曲率和圆弧边主曲率等数据。

图2　用于双稳态试验测试的附带温控箱的拉伸试验机　(a)经改装的实验平台;(b)温控箱中的内部加载情况Fig.2　Tensile testing machine with temperature control box for the bistable　(a)modified testing machine;(b)internal loading state in temperature

对于不同的温度环境下的稳态转变实验，通过调整温控箱的温度，重复进行上述实验操作过程可以得到。

2　结果及分析

2.1温度对稳态转变载荷的影响

考虑试件的材料特性即其玻璃态转化温度Tg为85℃的限制，对3种不同铺层层数的反对称圆柱壳分别在20 ℃，40 ℃，60 ℃和80 ℃的温度下进行稳态转变实验，研究温度场对两种稳态转变过程的影响。从snap-through实验过程观察到，由于压头以5 mm/min的加载速率从上至下位移加载，先接触圆柱壳的两直边，使两直边逐渐弯曲变形，当达到载荷的最大值后，压头还一直接触圆柱壳的两直边，同时压头继续下移加载，圆柱壳达到一定变形后，脱离与压头的接触，突然转变达到第二稳态，压头停止下移加载，其中把载荷的最大值称为稳态转变载荷。snap-back过程以第二稳态为初始状态，采用同样加载方式，使其转变回到第一稳态。

图3给出了3种试样在20 ℃，40 ℃，60 ℃和80 ℃的温度下进行snap-through过程反对称圆柱壳所受载荷随壳直边中点的位移(即压头向下加载时的位移)变化的关系曲线和20 ℃，40 ℃，60 ℃时Snap-back稳态转变过程关系曲线，试样1,2的80 ℃的snap-back曲线由于较大的扭曲率而未获得，同时图4给出了三个试件稳态转变载荷随温度变化趋势图。

从图3可以看出，对于snap-through过程，在加载初期反对称圆柱壳所受载荷随着位移的增大而明显增大，在达到峰值(稳态转变载荷)后又快速减小为零。对于snap-back过程，在加载初期反对称圆柱壳所受载荷随着位移的增大而明显增大，在达到峰值(即稳态转变载荷)后又快速减小至一局部极小值，经过局部缓慢增大后迅速下降为零，表明此时试件已完成稳态转变，达到第二稳态。由图3和图4可以发现：(1)在同一温度下，对比3个不同试样(即不同铺层)的snap-through 过程和snap-back过程的载荷—位移曲线，可以发现随着铺层的增加，稳态转变载荷有明显的增加。(2)通过比较snap-through与snap-back过程的载荷—位移曲线，可以发现，snap-through的稳态转变载荷明显大于snap-back的稳态转变载荷。snap-back的位移载荷曲线在曲线下降时有再上升的变化过程，与snap-through的曲线下降过程有明显的不同。(3)对于同一种试样，稳态转变载荷在snap-through过程中随着温度的升高呈现下降趋势；在snap-back过程中随着温度的升高反而呈现上升趋势，即低温时从第二稳态回复到第一稳态比第一稳态到第二稳态转变更容易。

以上分析表明，随着铺层层数的增加，反对称圆柱壳有了更大的结构刚度，在相同的压头位移距离下，所需要的加载力明显增加，层数越多的反对称圆柱壳也就拥有了更高的承载能力。这种随层数增加承载能力同时增加的现象在不同温度的影响下的规律保持不变。snap-back的载荷位移曲线与snap-through的载荷位移曲线有较大的不同，原因在于不同温度下，第二稳态时的反对称圆柱壳相比第一稳态时的圆柱壳曲率半径有了改变，并且第二稳态时相比第一稳态有更大扭曲率的存在。复合材料树脂基底在高应变状态下由线弹性变为黏弹性[16]，在温度升高后，影响更剧烈。参考造成正交对称双稳态薄板在不同温度下所需稳态转变载荷变化的影响因素[13]，每层的树脂和纤维的力学性能受温度的影响，同时考虑到稳态转变载荷在局部上不符合整体随温度变化趋势(即在图4(a)的snap-through过程中，随着温度的升高，稳态转变载荷在整体上是减小的，而试样在80 ℃的稳态转变载荷比60 ℃的稳态转变载荷的大)，可能是因为该反对称圆柱壳是由含不同铺设角的单层板粘结而成，不同铺层间的层间剪切力会在不同温度下产生变化从而产生稳态转变载荷的局部变化。此外，反对称圆柱壳存在的制造缺陷和实验的测量误差也会对其造成影响。

图3　不同温度下3个试样的载荷-位移曲线Fig.3　Load-displacement curves of 3 specimens under different temperatures

图4　3个试件稳态转变最大临界载荷Fig.4　Snap load of the three specimens　(a)snap-through process;(b)snap-back process

2.2温度对稳态曲率的影响

对于Snap-through过程和Snap-back过程，分别在20 ℃,40 ℃,60 ℃和80 ℃的温度下进行稳态转变的实验。通过前述数字图像处理技术，得到第一稳态的主曲率半径R1和第二稳态的主曲率半径R2，以及第一稳态的扭转角θ1和第二稳态的扭转角θ2。采用Guest和Pellegrino的双参数模型[18]来表示圆柱壳第一稳态和第二稳态的的曲率情况，即利用主曲率C和初始曲率轴线方向与主圆柱壳轴线夹角θ,及通过公式kxy=Csin2θ获取扭曲率来表示曲率变化情况)。其中主曲率C为通过前述数字图像处理技术得到的主曲率半径的倒数(即为下表3和表4的第二稳态主曲率kx2和第一稳态主曲率ky1，初始曲率轴线方向与主圆柱壳轴线夹角θ为测得第一稳态的扭转角θ1和第二稳态的扭转角θ2的二分之一。表3和表4的第一稳态扭曲率kxy1和第二稳态扭曲率kxy2则是通过前述公式计算得到。表2给出了试样1和试样3在不同温度下第一稳态和第二稳态主曲率半径。结果表明：随着温度的增加，试样主曲率半径R均在不断减小。

表3给出了试样2第二稳态时的主曲率和扭曲率。表4给出了试样3第一稳态时的主曲率和扭曲率。由表3～4可以发现，在温度的影响下，反对称圆柱壳发生了扭转情况，并且试件2第二稳态的扭曲率和试件3第一稳态的扭曲率都随着温度的增加扭转程度整体呈现增加的趋势。这可以说明反对称首先产生某个方向上的扭转变形，当温度影响不断增大时，扭转现象会在原扭转基础上不断加剧，从而产生扭曲率变化的趋势，但同时可以发现在实验的过程中有局部上减小的现象。首先，考虑到研究的反对称圆柱壳铺设角为45°，通过理论分析得到随着温度的升高，试件在第一稳态和第二稳态时扭曲率都会增加[19]；其次，温度的升高，反对称圆柱壳内残余应力释放会导致扭曲率的变化。复合材料树脂基底在高应变状态下由线弹性变为粘弹性，在温度升高后，影响更剧烈。当然，实验操作误差或测试误差等也会有影响。

反对称圆柱壳具有较好的结构设计性，空间利用率比较好，并且质量轻。不同层数的反对称圆柱壳在不同的温度影响下有明显的曲率变化，层数越多的反对称圆柱壳拥有更大的结构刚度，抵抗温度影响的能力更强，扭转程度比层数少的小。在相同层数圆柱壳的情况下的温度增加和在同一温度下层数的减少会使圆柱壳更容易发生扭转，如何消除温度对双稳态结构曲率的影响，防止扭转的产生是进一步要解决的问题。

表2　试样1和试样3在不同温度下测量的实验主曲率半径

表3　试样2第二稳态主曲率kx2和第二稳态扭曲率kxy2

表4　试样3第一稳态主曲率ky1和第一稳态扭曲率kxy1

2.3存放时间对双稳态结构性能的影响

树脂基底具有黏弹性特性[16]，考虑存放时间对其双稳态结构变形的临界载荷的影响并进行试验测试。表5和表6中列出了试样1和2在不同温度下的两次相同实验操作过程中的载荷，两次实验时间间隔为25天。

通过实验发现第二次实验相比第一次实验的Snap-through过程的稳态转变载荷Ft有较明显的降低，表明该材料在工程使用中要考虑基底的材料性能，避免因其基底性能的改变影响双稳态结构自身功能和变形的实现。

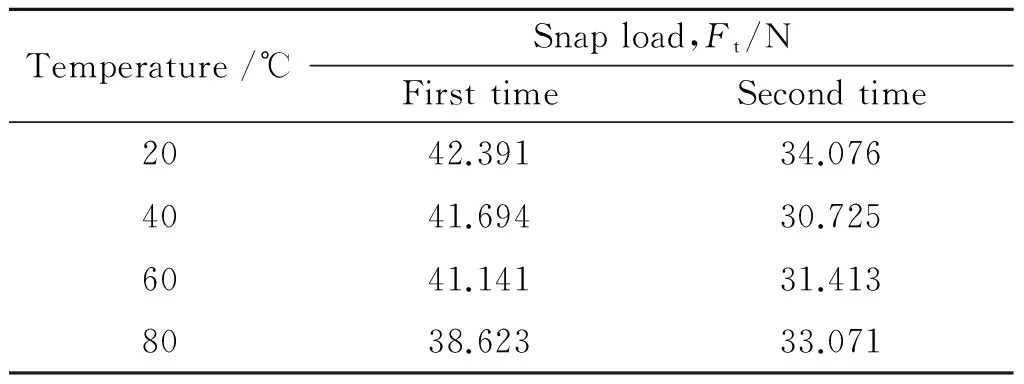
表5　试样1两次相同实验条件下的稳态转变载荷

表6　试样2两次相同实验条件下的稳态转变载荷

3　结　论

(1)温度对稳态转变载荷、初始稳态和第二稳态曲率影响较大；随着温度的增加，反对称铺设圆柱壳在snap-through过程所需要的稳态转变载荷逐渐减小，而在snap-back过程所需要的稳态转变临界载荷逐渐增大，但是对比snap-through过程和snap-back过程的稳态转变载荷，前者明显大于后者。同时再考虑两个稳态的扭曲率，整体上都是随温度的升高扭曲率不断增加，只是局部有减小的情况。

(2)存放时间对双稳态结构稳态转变载荷也有较大的影响，稳态转变载荷随存放时间增加会有较大幅度的降低。

[1] ZHANG Z, WU H, HE X,etal. The bistable behaviors of carbon-fiber/epoxy anti-symmetric composite shells [J]. Composites Part B：Engineering, 2013, 47: 190-199.

[2] 韩志勇,王晓梅,左进奎,等. 碳纤维树脂基复合材料电热损伤温度场研究[J]. 中国民航大学学报,2013,02:63-66.

(HAN Z Y, WANG X M, ZUO J K,etal. Research on temperature field of CFRP electric-thermaI damage[J]. Journal of Civil Aviation University of China,2013,02:63-66.)

[3] 王世明. 温度与湿度环境对碳纤维复合材料力学行为的影响研究[D].南京：南京航空航天大学,2011.

(WANG S M. Effect of temperature and humidity environment on mechanical properties of carbon fiber composites[D]. Nanjing: Nanjing University of Aeronautics & Astronautics,2011.)

[4] 张晓艳. 非对称正交铺层双稳态复合材料的发展与应用[J]. 航空制造技术,2012,17:70-71+89.

(ZHANG X Y. Development and application of unsymmetric bi-stable composites[J]. Aeronautical Manufacturing Technology,2012,17:70-71+89.)

[5] 董文俊,孙秦. 不对称铺层复合材料层合板的双稳态机理分析[J]. 机械科学与技术,2012(3):461-464+469.

(DONG W J,SUN Q. The mechanism analysis of bi-stable asymmetric composite laminates[J]. Mechanical Science and Technology,2012(3):461-464+469.)

[6] 张征,吴和龙,吴化平,等. 正交铺设碳纤维复合材料结构的双稳态特性研究[J]. 功能材料,2013(2):236-239.

(ZHANG Z, WU H L, WU H P,etal. Bi-stable characteristics of orthogonal unsymmetric carbon-fiber composite structure[J]. Functional Materials,2013(2):236-239.)

[7] GUDE M, HUFENBACH W, KIRVEL C. Piezoelectrically driven morphing structures based on bistable unsymmetric laminates[J]. Composite Structures, 2011; 93: 377-382.

[8] PIRRERA A, AVITABILE D, WEAVER P M. On the thermally induced bistability of composite cylindrical shells for morphing structures, International Journal of Solids and Structures, 2012，49: 685-700.

[9] ZHANG Z, WU H, WU H,etal. Bistable characteristics of irregular anti-symmetric lay-up composite cylindrical shells[J]. International Journal of Structural Stability and Dynamics，2013，13(6)：1350029.

[10] ZHANG Z, WU H, YE G,etal. Systematic experimental and numerical study of bistable snap processes for anti-symmetric cylindrical shells [J]. Composite Structures, 2014,112: 368-77.

[11] TSAI C L, WOOH S C, HWANG S F,etal. Hygric characterization of composites using an antisymmetric cross-ply specimen[J]. Experimental Mechanics, 2001, 41(3): 270-276.

[12] YOUSSEF Z, JACQUEMIN F, GLOAGUEN D,etal. A multi-scale analysis of composite Structures: application to the design of accelerated hygrothermal cycles[J]. Composite structures, 2008， 82: 302-309.

[13] MOORE M, ZIAEI-RAD S, SALEHI H. Thermal response and stability characteristics of bistable composite laminates by considering temperature dependent material properties and resin layers[J]. Applied Composite Materials, 2013， 20: 87-106.

[14] MOORE M, ZIAEI-RAD S, FIROUZIAN-NEJAD A. Temperature-curvature relationships in asymmetric angle ply laminates by considering the effects of resin layers and temperature dependency of material properties[J]. Journal of Composite Materials, 2014; 48: 1071-1089.

[15] ECKSTEIN E, PIRRERA A, WEAVER P M. Morphing high-temperature composite plates utilizing thermal gradients[J]. Composite Structures, 2013, 100: 363-372.

[16] YANG J, XIONG J, MA L,etal. Vibration and damping characteristics of hybrid carbon fiber composite pyramidal truss sandwich panels with viscoelastic layers[J]. Composite Structures, 2013，106: 570-580.

[17] 吴和龙. 反对称双稳态复合材料结构的实验与数值模拟研究[D].杭州：浙江工业大学, 2012.

(WU H L. Experimental investigation and numerical simulation for the anti-symmetric bistable composite structure[D].Hangzhou: Zhejiang University of Technology,2012.)

[18] GUEST S, PELLEGRINO S. Analytical models for bistable cylindrical shells[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 2006, 462(2067): 839-854.

[19] ZHANG Z, YE G, WU H,etal. Thermal effect and active control on bistable behaviour of anti-symmetric composite shells with temperature-dependent properties[J]. Composite Structures, 2015；124: 263-271.

(责任编辑：张峥)

Thermal Effect on Bistable Behaviour of T700/3234Anti-symmetric Cylindrical Shells

ZHANG Zheng1,PAN Hao1,YE Gangfei1,LI Chen1，2,WU Huaping1,CHAI Guozhong1

(1.Key Laboratory of E&M, Ministry of Education & Zhejiang Province, Zhejiang University of Technology, Hangzhou 310032， China; 2.Department of Quality and Safety Engineering, China Jiliang University, Hangzhou 310018, China)

The temperature effects on the bi-stable characteristics of T700/3234 anti-symmetric carbon-fiber composite structure were studied. Three different layup specimens were prepared through composite molding process.The two points loading method was used in the experiment. The modified experimental testing machine (the experimental testing machine could be used to induce the bistable composite shell to snap between the two stable shapes, and continually capture the data in the experimental process.) was related to tensile testing machine at present. The load-displacement curvatures under the temperature of 20 ℃,40 ℃,60 ℃ and 80 ℃ were given. The snap load was recorded and the photos were taken in the experimental process. After the experiment, the detailed data of curvature and twisting curvature were obtained by image processing technology. The variation law of the coiled-up radius, out-of-plane displacement, maximum snap-through and snap-back loads were analyzed. The effect on the composite structure was also discussed.The result shows that the thermal effect is vital to the bistable snaps process, and corresponding influence trends to the snap through and snap back process are given.

carbon-fibre composite；antisymmetric layup shell；Bi-stable characteristics；temperature field

2015-04-01；

2016-01-23

国家自然科学基金资助项目(51675485, 11002126)；浙江省自然科学基金(LY15E050016)；教育部高等学校博士学科点专项科研基金 (20123317120003)；中国博士后科学基金(2013M540498，2014M561787)

张征(1979—)，男，博士，副教授，主要从事复合材料力学和数值分析方法研究，(E-mail)zzhangme@zjut.edu.cn。

10.11868/j.issn.1005-5053.2016.5.012

TH123

A

1005-5053(2016)05-0070-07