层次分析法在0-3岁早期教育机构发展质量评价体系中的应用

2016-10-22李丽红

赤峰学院学报·自然科学版 2016年18期

关键词：早教分析法排序

李丽红

（文山学院　教育科学学院，云南　文山　663000）

层次分析法在0-3岁早期教育机构发展质量评价体系中的应用

李丽红

（文山学院教育科学学院，云南文山663000）

随着脑科学研究的不断发展，0－3岁早期教育越来越受到家长们的重视.面对大量应动而生的早教机构，家长该如何进行有效的选择成了最受关注的话题.本文应用层次分析法建立0～3岁早期教育机构发展质量层次结构模型，构建两两判断比较矩阵，求出层次单、总排序并进行一致性检验，选取某地区三所早教机构进行具体的算例分析，最终分析帮助家长依据师资队伍、课程设置、环境创设和政府管理的权重来有效选择0－3岁早教机构.该模型切合实际，验证了0－3岁早期教育机构发展质量评价指标的合理性、评价方法的有效性.此评价方法对家长、早教机构、早教主管部门科学有效地规划早教发展具有一定的参考意义.

层次分析法；早教发展质量；评价体系；应用

随着脑科学研究的不断发展，0-3岁早期教育越来越受到家长们的重视，孩子将越来越早地接受早期教育己经成为了一种发展趋势.面对我国大量早教机构如雨后春笋般的涌现，0-3岁早期教育机构发展的质量好坏成为了早期教育发展的关键.如何建立一套符合中国国情的、高效的0-3岁早期教育机构发展的质量评价体系已成为早期教育改革中的重难点问题.本文通过运用层次分析法的数学模型，建立0～3岁早期教育机构发展质量评价权重体系，家长可依据此评价体系科学有效地甄别和选择适合的早教育机构.

1　建立0～3岁早期教育机构发展质量层次结构模型

为了使家长找到比较满意的0～3岁早期教育机构，首先要建立0～3岁早期教育机构发展质量层次结构模型，它分为三个层次：目标层O，即家长对0～3岁早期教育机构质量满意程度；准则层B，包括环境创设、课程设置、师资建设、政府管理四个方面；方案层P，由A、B、C三个早教机构组成［1］.如图1所示.

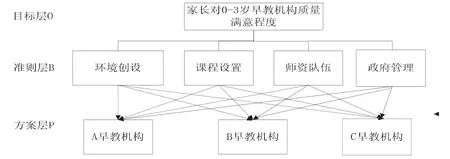
图1　0～3岁早期教育机构发展质量层次结构模型

2　构建两两判断比较矩阵

2.1确定准则层对目标层的权重

根据准则层的四个不同因素对家长对0-3岁早教机构质量满意程度的目标层的影响权重，用数字1-9及其倒数作为矩阵的标度，从而对成对比较矩阵进行赋值，得到这四个选择因素对0-3岁早教机构质量满意度O的两两比较矩阵：

2.2确定方案层对准则层的权重

用同样的方法，方案层（即家长可选择的0-3岁早教机构）的三个因素p,p,p（A、B、C三家早教机构）对准则层的四个选择因素中的每个因素的判断矩阵Ai（i=1,2,3,4），分别为：

通过以上两步运算，家长对0-3岁早教机构质量评价中的环境创设、课程设置、师资队伍和政府管理四个因素的在自己心中的重要程度进行了量化和对比，确定准则层对目标层的权重和方案层对准则层的权重.

3　进行层次排序和一致性检验

3.1进行层次单排序和一致性检验［2］

一致性指标CI由公式为：

其中：λmax为判断矩阵的最大特征值，n为判断矩阵的阶数.

一致性比例CR的计算由公式为：

其中：CR指随机一致性比率，CI为判断矩阵的一致性指标，RI为平均随机一致性指标.

当CR＜0.1时，表示判断矩阵通过一致性检验，权系数分配合理.

按照上述的方法，求得0～3岁早期教育机构发展质量层次结构模型中矩阵A-Ai（i=11-13）的最大特征值λmax=4.0788，CI=（λmax-n）/（n-1）= 0.0263，CR=CI/RI=0.0263/0.8931=0.02294＜0.1，因此，我们可以认为判断矩阵通过了一致性检验.0～3岁早期教育机构发展质量准则层环境创设、课程设置、师资建设、政府管理的权重w=0.1207| 0.2672|0.5087|0.1033.

同理还要对0～3岁早期教育机构发展质量方案层的A1-Ai（i=11-13），进行一致性检验［3］，通过计算，A1-Ai（i=11-13）的λmax=3.7641，CI=（λmax-n）/（n-1）=（3.7641-3）/2=0.38205，CR=CI/RI= 0.38205/0.5149=0.7420＜0.1，因此，我们可以认为判断矩阵通过了一致性检验.

对0～3岁早期教育机构发展质量方案层的A2-Ai（i=11-13），进行一致性检验，通过计算，A2-Ai（i=11-13）的 λmax=3.0385，CI=（λmax-n）/（n-1）=（3.0385-3）/2=0.01925，CR=CI/RI=0.01925/0.5149=0.0374＜0.1，因此，我们可以认为判断矩阵通过了一致性检验.

对0～3岁早期教育机构发展质量方案层的A3-Ai（i=11-13），进行一致性检验，通过计算，A3-Ai（i=11-13）的 λmax=3.0037，CI=（λmax-n）/（n-1）=（3.0037-3）/2=0.00185，CR=CI/RI=0.00185/0.5149=0.00359＜0.1，因此，我们可以认为判断矩阵通过了一致性检验.

对0～3岁早期教育机构发展质量方案层的A4-Ai（i=11-13），进行一致性检验，通过计算，A4-Ai（i=11-13）的 λmax=3.0183，CI=（λmax-n）/（n-1）=（3.0183-3）/2=0.00915，CR=CI/RI=0.00915/0.5149=0.0178＜0.1，因此，我们可以认为判断矩阵通过了一致性检验.

3.2进行层次总排序及一致性检验

层次总排序的程序是在层次单排序的基础上，从高到低逐层进行的，计算公式如下：

在层次单排序的基础上，再计算出方案层（可选择的0-3岁早教机构）对目标层（家长对0-3岁早教机构满意程度）的层次总排序.按照上述的方法，求得层次单、总排序和一致性检验各数据见下表2.

从表2可以看出，在层次总排序中，A、B、C三个早教机构的权重分别为w=0.3780|0.44550| 0.1765.由此可见，B早教机构的权重最重，A早教机构次之，C早教机构最小.因此，B早教机构的总体评价最好，其后依次是A早教机构和C早教机构.同时，家长选择0-3岁早教机构考虑的各因素排序为：师资队伍、课程设置、环境创设和政府管理［4］.因此，家长选择0-3岁早教机构的过程中，可以引导家长在选择时运用层次分析法进行选择，综合0-3岁早教机构发展质量的四个方面因素，最终科学有效的选择最适合自己孩子的早教机构.