并联Buck变换器非线性加载控制策略

周敏，刘勇，陈奕良，胡合壮，彭昊

（湘潭大学信息工程学院，湖南 湘潭 411105）

并联Buck变换器非线性加载控制策略

周敏，刘勇，陈奕良，胡合壮，彭昊

（湘潭大学信息工程学院，湖南 湘潭 411105）

为了提高并联Buck变换器的加载响应速度，分析了传统CCM模式下并联Buck变换器的加载过程，并基于电荷平衡原理提出了并联Buck变换器多模式切换控制方案。以并联Buck系统加载后预期稳态电感电流平均值、实际电感电流平均值、电容充放电量的对应关系为依据，给出了非线性控制模式的切换条件和切换时间的计算方法。仿真和试验结果表明，非线性加载控制下并联Buck变换器较传统控制模式下的并联Buck变换器具有更快加载响应速度。

并联Buck；快速加载；非线性控制；多模式切换

近年来随着电子计算机和数字处理技术的飞速发展，生产生活对电源系统的要求越来越高。传统的集中式供电系统由于具有可靠性差、开发周期长、设计制作成本高等缺点已不能满足其发展需求。多模块并联供电系统具有以下特点：

1）单个模块提供整个系统功率的1/n，可实现低电压、大电流、大功率输出；

2）缩短了系统的研发周期，降低了开发成本；

3）可实现N+M个模块的冗余供电，提高系统的可靠性；

4）方便实现系统容量的扩展等特点，已成为电源系统发展的主流趋势。

由于并联技术的采用，并联供电系统动态和稳态工作时都保持良好的工作特性成为多模块直流变换器设计的主要研究问题之一［1-2］。目前，对并联系统模块间的均流控制和环流抑制的相关研究较多，而对其瞬态特性研究较少［3-6］。由于并联系统模块间具有强耦合性、强非线性等特性，因而在单模块直流变换器取得非常好的稳态和动态特性的相关控制策略在多模块并联系统中已无法适应［7-15］。

本文在电压、电流双环控制的基础上，根据电荷平衡原理，以并联Buck系统加载后预期稳态电感电流平均值、实际电感电流平均值、电容充放电量的对应关系为依据，提出了一种非线性控制模式的切换条件及切换时间的计算方法。

仿真及实验结果表明，基于多模式切换的非线性加载控制策略能在保证系统稳定性的前提下提高系统的加载响应速度。

1　并联Buck变换器传统加载控制

1.1传统加载控制策略

在如图1所示的并联Buck变换器电路中，假设所有的电路元件均为理想元件。稳态工作时采用电压、电流双环控制。而且在加载之前Modle-1已经工作在稳态模式下，稳定输出电压为Uo，输出电流为Io。为了防止Modle-2在并入过程中由于两模块的输出电压不一致而产生电流冲击，给Modle-2的电容预先充一定电荷，使其空载输出电压等于系统的稳态输出值Uo。当负载增加的瞬间，开关K导通，两模块开始同时向负载供电，直到两模块都达到稳态后加载过程结束，各并联系统开始为负载提供额定大小的功率。

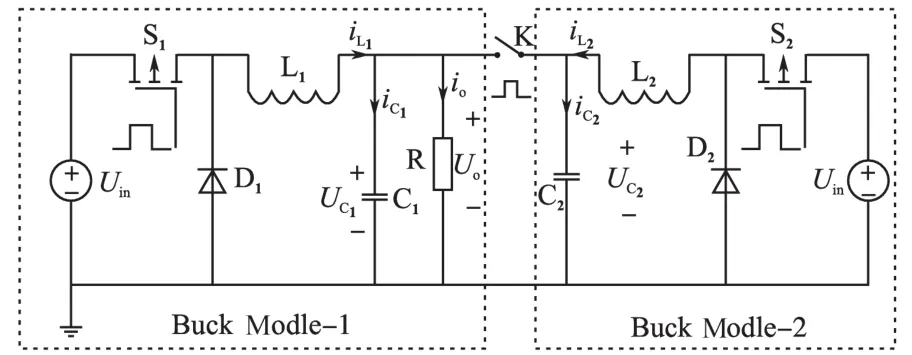
图1　并联Buck变换器拓扑结构Fig.1　The network topology structure of paralleled Buck converter

1.2传统加载瞬态特性分析

负载在t0时刻阶跃加载（Δio=Io），图2为Modle-2的电感电流iL2和输出电压uo的波形。

图2　传统并联Buck变换器加载瞬态波形Fig.2　Transient response waveforms of traditional paralleled Buck converter under a step load increased

图2中，t0=0为加载时刻；t1为加载后电感电流iL2的平均值第1次达到稳态值时刻；t2为电感电流iL2达到最大时刻；tsd为加载后输出电压稳态恢复时刻。

当t0=0时，负载发生阶跃变化，负载电流由Io跃变为2Io，开关K导通，由于电感电流不能突变，此时电感电流iL2仍为零，负载电流io为iL1，iC1，iC2之和，则在加载时刻t0后系统的瞬态过程如下。

1）t0—t1期间，开关管S2导通，iL2开始迅速增加，同时iL1也在控制器的作用下增长，电容C1，C2开始放电，电容电压开始减小。t1时刻iL2增大到稳定值，由于iL1的影响，电容C1，C2于t1之前某一时刻tvi停止放电，输出电压降到最小值Uomin。

2）t1—t2期间，电源开始在控制器的作用下经过电感给负载供电，同时为电容充电，电感电流和输出电压同时开始增加，t2时电感电流达到最大值。

3）t2—tsd期间，开关管S2断开，电感电流开始回落，但由于其值仍大于稳态值，所以输出电压将继续增大到某一值后随电感电流一起回落到各自的稳态值，加载过程结束。

在加载过程中，由于电感电流iL2是由0开始上升直到稳态，这使得电容C1，C2充放电速率和步调不一致。iC1和iC2变化曲线呈强烈的非线性，所以文献基于通过直接计算电容释放和补充的电荷量来求解单模块的最优加载稳态调节时间的方法在双模块并联系统中已经无法适应［16］。

因此本文根据并联Buck变换器加载过程中的电感电流的瞬态特点，提出了一种基于预期加载后稳态电感电流平均值、实际电感电流平均值以及电容放电和充电的电荷量的对应关系来计算加载过程中电容充放电平衡时刻的方法。并以此作为开关管通断和控制模式切换时刻的理论依据，下面将对其计算方法和控制原理进行分析。

2　并联Buck变换器非线性加载控制

2.1非线性加载控制策略

多模式切换Buck并联系统加载控制和传统模式加载控制的预处理和并入时刻仅由系统稳态输出电压和加载的时刻所决定，在此不考虑加载时刻对并联Buck变换器加载瞬态性能影响。

如图1所示，在加载瞬间开关K和开关管S2同时导通，系统由双闭环控制模式切换为非线性控制模式，并在电感电流iL2重新回到稳态时刻，让控制器切换成双闭环控制模式。在此期间，Model-1仍工作在线性控制模式下，开关管S1以稳态时的占空比开通和关断。本文所研究的关断时刻，是指在加载过程中输出电压无超调的情况下系统恢复到稳定运行状态的最短时间点。由于实际加载过程中Modle-1的电感平均值电流和负载电流的扰动对Modle-2的电感电流影响较小，以下将忽略其扰动对并联Buck变换器加载特性的影响。

2.2非线性加载瞬态特性分析

在t0=0时刻负载阶跃加载（Δio=Io），图3为加载后Buck并联系统Modle-2预期电感电流、实际电感电流、输出电压的瞬态波形。

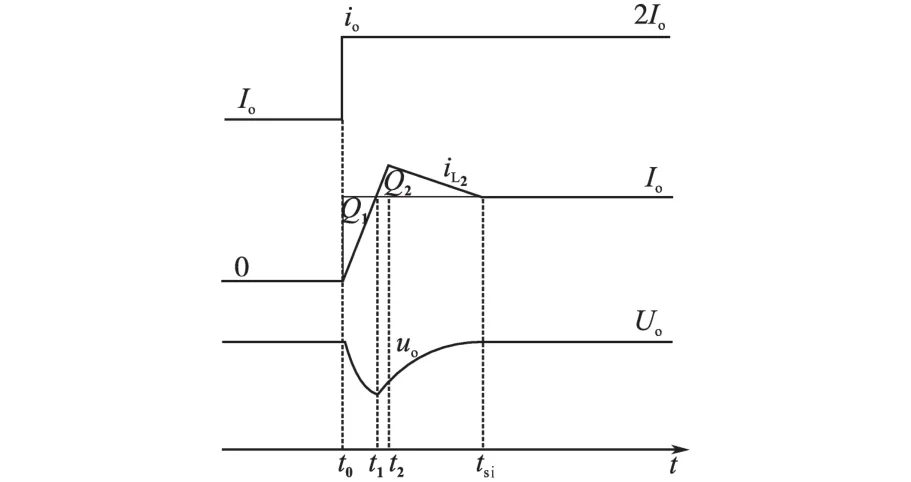
图3　非线性控制下并联Buck变换器加载瞬态波形Fig.3　Transient response waveform of nonlinear control paralleled Buck convrter under a step load increased

图3中，t1为输出电压达到最小值即电容停止放电时刻，t2为电感电流达到最大值即开关管S2关闭时刻，tsi为电感电流下降达到稳态值同时输出电压也恢复稳态的时刻。

当t=t0=0时刻，负载电流由Io跃变为2Io，电容C1，C2的总输出电流为 Io。此时iL1=Io，iL2=0保持不变。由图3可知，负载跃变后并联Buck变换器的瞬态调节过程如下。

1）t0—t1期间开关管S2导通，电源给电感充电，电感L1的电流保持不变，而电感L2的电流线性增加。此时，输出电容C1，C2放电，使负载电流维持在2Io，同时电容端电压开始下降。当t=t1时，电感电流iL2上升至稳态值，负载电流可由iL1和iL2提供，电容停止放电，电容电压跌落到最低点Uomin。

2）t1—t2期间电源继续向电感充电，iL2超过其稳态平均值后继续线性增加。于是电感电流除了给负载提供能量外，还为电容充电，输出电压开始回升。当t=t2时，开关管S2断开，iL2开始下降。

3）t2—tsi期间电感电流iL2开始线性回落，但由于其值仍大于Io，iL2将继续给电容充电，直到t=tsi时iL2=Io。同时输出电压恢复到稳态值Uo，加载瞬态过程结束。

由图1、图3可知电感L2的电流瞬态表达式为

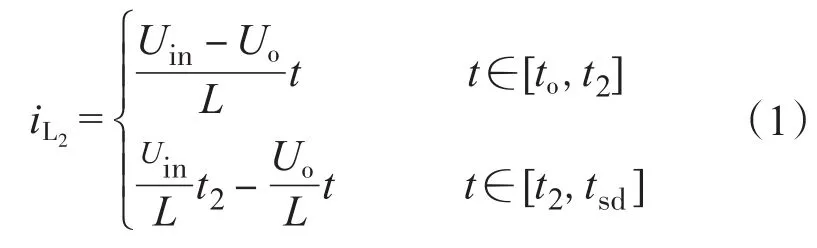
式中：Uin,Uo为输入输出电压额定值。

电容停止放电时刻t1，根据iL2=Io，可得：

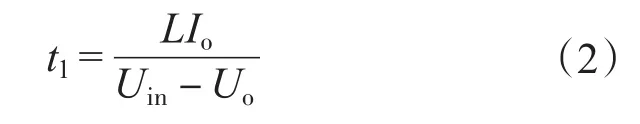
式中：Io为额定电流值。

由上面的分析可知，在t1时刻，输出电压将达到最小值Uomin。而在此期间电感电流iL2提供的电荷量与负载消耗的电荷量之差Q1等于电容释放的电量，根据电容两端电压公式得：

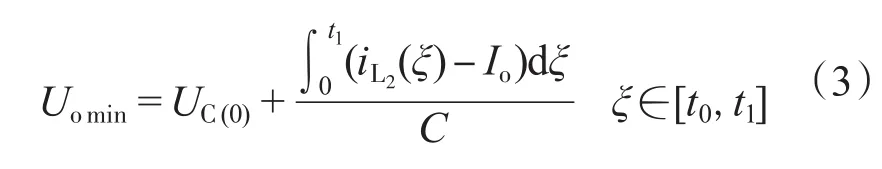
式中：C=C1+C2；UC（0）为电容初始的电压值。

在t1—t2期间，电感电流iL2除了为负载提供能量外，其余电流都用来为电容充电。为使电感电流iL2和输出端电压在tsi同时恢复到稳态，电感电流iL2给电容充电电量Q2须等于Q1。由图3可得：

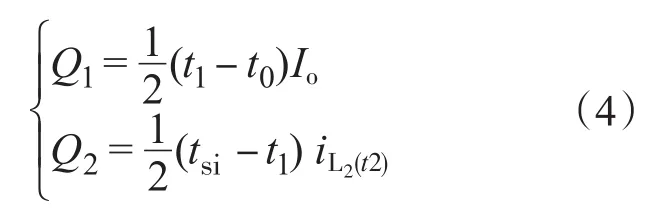
令Q1=Q2；联立式（1）、式（4）可得输出电压的稳态调节时间tsi：

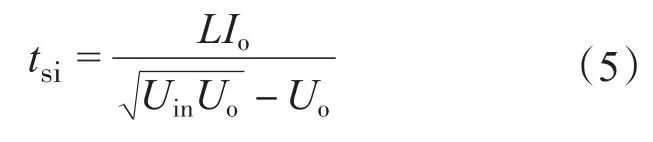
又由图3可知，电感电流iL2上升和下降的斜率分别为m1,m2：

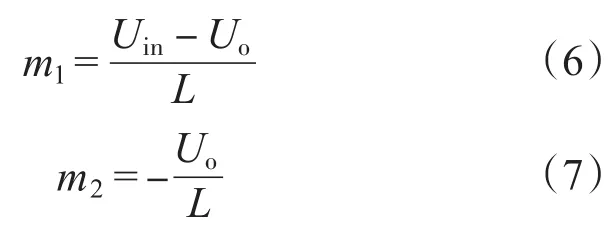
由电感电流在t1，tsi时刻相等，可得：

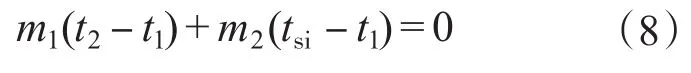
联立式（2）、式（6）～式（8）可得：

由以上分析过程可计算出双模块Buck加载过程中控制模式最优切换时刻和理论上的加载性能指标。

3　仿真分析

图4为基于多模式控制下的并联Buck变换器控制仿真电路方案。

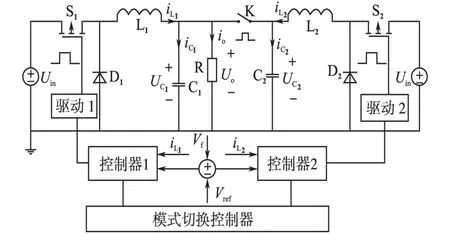
图4　多模式切换并联Buck变换器原理框图Fig.4　Multi-mode switching paralleled buck converter principle diagram

图4中，Buck并联系统中单模块的电路参数和设计指标如下：输入电压Vin=110 V，输出电压期望Vo=48 V，负载电阻R在t=0.1 s时，由4.8 Ω跃变为2.4 Ω，滤波电感L1=L2=675 μH，滤波电容C1=C2=100 μF。控制器1、控制器2结构参数一致，均采用电压、电流双闭环控制。

模式切换控制器主要由检测模块和运算模块组成。在系统加载时，检测模块通过检测系统的输出电流值io的变化值Δio来计算非线性加载控制模式的切换时刻。并以此来改变控制器的工作模式，从而实现快速加载控制。

由式（3）、式（5）、式（9）可得，该双模块Buck并联系统的加载时刻和各控制模式切换时间to= 0.1s；t2=0.10018s；tsi=0.10027s；Uomin=45.3V。

利用Matlab对两种控制模式下Buck变换器进行仿真，图5、图6分别为负载电流由10 A跃变为20 A的传统Buck并联加载控制和多模式切换加载控制的加载输出电压、输出电流、电感电流及开关管驱动仿真波形图。

由图5、图6可知，传统模式控制下Buck变换器并联系统的加载响应特性为：输出电压Uo1min=45.7 V；调节时间Δt1=500 μs多模式切换控制下Buck变换器并联系统的加载响应特性；输出电压Uo2min=45.7 V；调节时间Δt2=250 μs，多模式切换控制比传统控制调节速度提升了将近1倍，可见基于多模式切换的双模块Buck变换器的瞬态特性优于传统模式控制下的Buck变换器。

由于多模式切换控制下的仿真结果与理论计算值Uomin=45.3 V，Δt=270 μs近似相等，证明理论计算的正确性，而其误差是由于忽略了Modle-1的电感平均值电流和负载电流的扰动造成的。

图5　传统加载控制仿真波形Fig.5　The simulation waveforms of the traditional loading control

图6　非线性加载控制仿真波形Fig.6　The simulation waveforms of the nonlinear loading control

4　实验验证

实验电路如图7所示，试验参数与仿真参数一致。其中控制器采用型号为STC12C5A60S2的单片机，驱动电路采用Buck电路专用驱动芯片M57959L。

图8为负载从10 A加载到20 A时非线性加载控制下并联Buck变换器的实验波形。由图8可知，并联Buck变换器的输出电压跌落量为3 V，稳态调节时间260 μs，实验结果与理论计算和仿真结果近似相等，证明了理论的正确性。

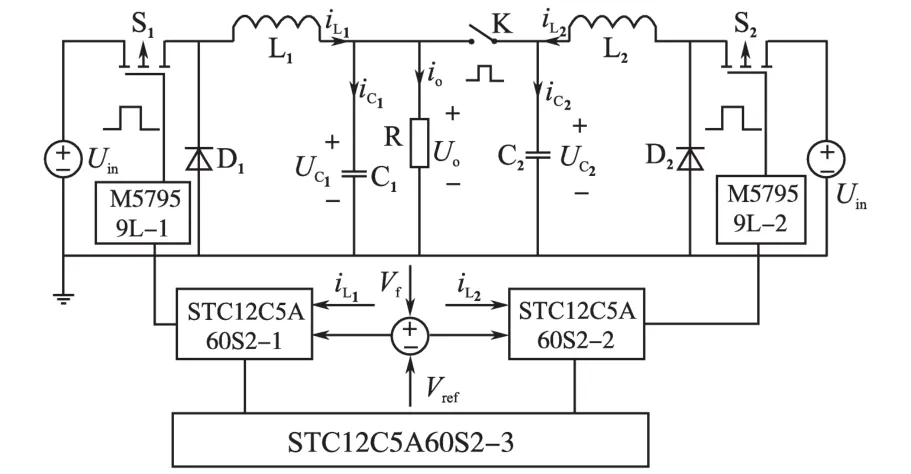
图7　实验电路图Fig.7　The circuit diagram

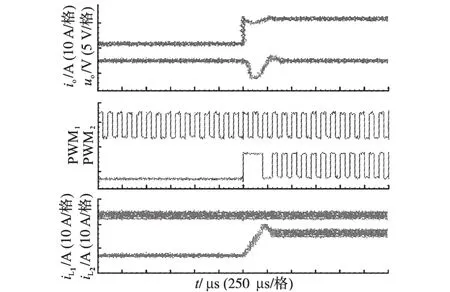
图8　非线性加载控制实验波形Fig.8　Experimental waveforms of the nonlinear loading control

5　结论

本文在基于传统的并联Buck变换器的基础上，根据双模块Buck变换器的加载过程中的电感电流（平均值近似呈线性）的瞬态特点以及预期稳态电感电流平均值、实际电感电流平均值以及电容放电和充电的电荷量的对应关系提出和实现了并联Buck变换器非线性加载控制策略，仿真和实验的对比研究表明：该控制策略能在保障系统闭环稳定的前提下有效地提高和改善多模块Buck变换器的加载特性，对实际工程应用有很好的指导意义。

［1］Zhou X，Xu P，Lee F C.A High Power Density，High Efficiency and Fast Transient Voltage Regulator Module with a Novel Current Sensing and Current Sharing Technique［C］//Proceedings of the APEC，USA，1999：289-294.

［2］Mehas G J，Coonley K D，Sullivan C R.Converter and Inductor Design for Fast-response Microprocessor Power Delivery［C］//Proceedings of the 31st Annual Power Electronics Specialist Conference，USA，2000，3：1621-1626.

［3］林新春，段善旭，康勇，等.基于下垂特性控制的无互联线并联UPS建模与稳定性分析［J］.中国电机工程学报，2004，24（2）：33-38.

［4］张宇，段善旭，康勇，等.并联系统中谐波环流抑制的研究［J］.中国电机工程学报，2006，26（12）：67-72.

［5］Sun Xiao，Lee Y S，Xu Dehong.Modeling，Analysis，and Implementation of Parallel Multi-inverter Systems with Instantaneous Average-current-sharing Scheme［J］.IEEE Trans.on Power Electronics，2003，18（3）：844-856.

［6］Duan Shanxu，Meng Yu，Xiong Jian，et al.Parallel Operation Control Technique of Voltage Source Inverters in UPS［C］//IEEE Power Electronics and Drive Systems，Hong Kong，China，1999.

［7］Abdel-Rahman O.Transient Response Improvement in DC-DC Converters Using Output Capacitor Current for Faster Transient Detection［C］//Issa atarseh.Proceedings of the 38th Power Electronics Specialists Conference.Orlando，Florida，USA：IEW.E，2007.

［8］Dong Yan.Twisted Core Coupled Inductors for Microprocessor Voltage Regulators［J］.IEEE Transactions on Power Electronics，2008，23（5）：2536-2545.

［9］Lu D Dah-Chuan.A Single Phase Voltage Regulator Module（VRM）with Stepping Inductance for Fast Transient Response［J］.IEEE，TransOilPowerElectronics，2009，22（2）：417-424.

［10］Singh R P.Buck-derived Topology with Improved Step Down Transient Performance［J］.IEEE Trans on Power Electronics，2008，23（6）：2855-2866.

［11］王凤岩.V2控制Buck变换器分析［J］.中国电机工程学报，2006，26（2）：121-126.

［12］MEYER.An Optimal Control Method for Buck Converter Using a Practical Capacitor Charge Balance Technique［J］.IEEE TransactionsonPowerElectronics，2008，23（4）：1802-1812.

［13］Tan SC.General Design Issues of Sliding-mode Controllersin DC-DC Converters［J］.IEEE Transactions Oil Industrial Electronics，2008，55（3）：l160-1174.

［14］马皓.新型功率放大器时变滑模控制方案研究［J］.中国电机工程学报，2005，25（11）：55-59.

［15］Tan S C.Development of Sliding Mode Controllers for DC-DC Converters［D］.Hong Kong：Doctor Dissertation of Hong Kong Polytechnic University，2005.

［16］倪雨.Buck变换器最优负载瞬态特性分析［J］.中国电机工程学报，2010，30（24）：8-14.

Nonlinear Loading Control Strategy of Paralleled Buck Converter

ZHOU Min，LIU Yong，CHEN Yiliang，HU Hezhuang，PENG Hao
（College of Information Engineering，Xiangtan University，Xiangtan 411105，Hunan，China）

To improve the step-up response speed of parallelled power supply system，the loading of a traditional CCM Buck converter in parallel system was analyzed.based on the Charge balance principle，the method of multi-mode switching control in parallelled Buck converter was proposed.The switching condition and time of nonlinear control mode were given by the relationship among the expected steady-state average inductor current value，the actual average inductor current value and the charge capacitor containing.The simulation and experimental results show that the multi-module paralleled Buck converter under the control of nonlinear loading control strategy is faster response speed than the traditional one.

paralleled Buck converter；fast loading performance；nonlinear control；multi-mode switching

TM46

A

2015-07-26

修改稿日期：2016-04-11

大学生创新项目（2014xtusj26）

周敏（1993-），男，本科，Email：18390223633@163.com