单镜头运动颗粒三维定位方法

金娜，周骛，胡嘉睿，蔡小舒



单镜头运动颗粒三维定位方法

金娜，周骛，胡嘉睿，蔡小舒

(上海理工大学能源与动力工程学院，上海市动力工程多相流动与传热重点实验室，上海，200093)

在光学离焦测距原理的基础上，提出一种采用单镜头双相机的运动颗粒三维定位方法，搭建图像法颗粒测量装置，并就图像离焦模糊度与颗粒深度位置关系进行理论和试验研究。系统采用分光棱镜连接1个镜头和2个相机，使用信号发生器实现两相机的同步拍摄，通过接圈调节相机与镜头的距离，获取同一时刻同一物体不同模糊程度的2张照片，根据模糊度的对比获得颗粒的深度。试验中选取2个图像传感器与镜头距离的差值为4.2 mm，采用静止圆点进行离焦测距系统试验验证，相对误差在10%以内，并采用该系统对电解食盐水产生的气泡进行三维离焦测距试验。研究结果表明：该方法可行性良好；该装置可解决单镜头拍摄颗粒场的离焦二义性问题，实现无参考物条件下运动颗粒场的深度重构。

运动颗粒；单镜头双相机；离焦测距；空间定位；离焦二义性

颗粒相流动广泛存在于科学研究与工程领域中，例如旋风分离器中的颗粒三维旋转流动以及柴油机中的燃料喷雾等，由于其瞬态及空间三维特性，使颗粒粒径、速度、体积分数、流量等参数的测量具有很大难度。目前，用于颗粒场测量的方法主要基于粒子的多普勒效应[1]与粒子成像[2]。前者包括激光多普勒测速仪(LDV)[3]和相位多普勒粒子分析仪(PDPA)[4]，其中PDPA利用信号频率测量速度，利用信号相位测量粒径，但是这2种方法均对粒子球形度要求较高[5]。粒子成像技术应用最广的是粒子图像测速仪(PIV)，其三维信息的获取又分为双目视觉法和全息法。双目视觉法通过2套成像系统不同角度的成像对一定空间内的粒子进行三维定位，其匹配算法复杂，设备价格昂 贵[6]。数字全息粒子测速仪(DHPIV)将数字全息与PIV技术相结合，可以获得瞬时的三维流动结构和速度场，然而，被测物体的空间定位精确度低且数字全息图像重建复杂[7]。简单的单镜头背光成像方式可以提供丰富的三维颗粒场信息[8]，但是位于景深范围外的颗粒成像会产生离焦模糊现象，影响测量结果。而该模糊信息暗含了颗粒的深度位置信息，若能对颗粒的深度信息进行提取，则一方面可以实现颗粒粒径和体积分数的精确测量，另一方面可以获取颗粒场的三维空间分布。周烨锋等[9−12]通过图像的模糊程度提取物体深度的信息，不需要解决立体视觉或双目相机中的点匹配问题。PENTLAND[13]通过改变相机孔径参数获得2幅模糊程度不同的图像来恢复深度，在针孔孔径下会引入大量噪声，且去卷积算法产生的衍射效应降低整体效率。ZHOU等[14]通过使用一对编码孔径，使其拍摄图像场景频率互补的2张图像恢复物体深度，获得了高质量的深度信息，但对设备要求高。如上所述的离焦测距装置需要改变成像系统参数获取前后2张同一物体不同模糊度的照片，只能解决静态物体的离焦测距问题。为此，本文作者基于离焦测距光学原理，提出一种单镜头双相机的运动颗粒三维定位装置，采用分光棱镜连接该镜头和2个相机，通过调节相机与镜头之间的距离，获取同一时刻同一物体不同模糊程度的2张照片，根据模糊度的对比获得颗粒的深度信息。采用静止颗粒对系统进行离焦测距试验验证，其相对误差在10%以内，通过误差分析提出系统精度的改进措施，并对电解水运动气泡进行三维定位测量，验证方法的可行性。

1 单镜头双相机运动颗粒三维定位原理

1.1 离焦测距原理

物体成像的实质是物体上无数的点光源发出光线，通过镜头被传感器接收。点光源经由透镜的成像过程如图1所示[15]。图1中：为物点，其与镜头主平面距离即物距为；镜头焦距为；像点′位于最佳成像平面上，该平面与透镜主平面的距离即像距为。若实际成像平面偏离最佳成像面，则采集的图像会存在一定程度的离焦模糊。图1中，2个离焦面D1和D2到凸透镜主平面的距离分别为1和2，物点在成像面D1和D2上分别对应成像的弥散圆半径为1和2。

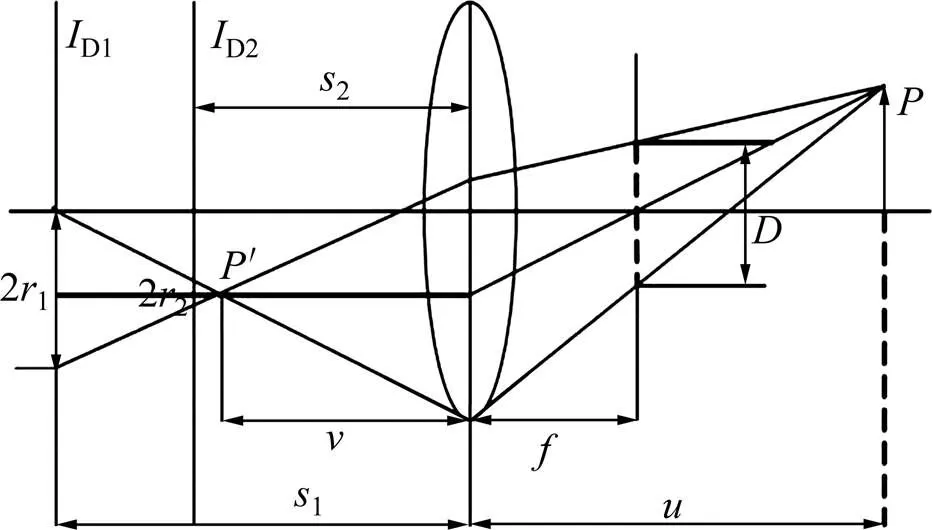
图1 离焦模糊成像过程

根据远心镜头成像原理，有

或

其中式(2)所适用条件为颗粒最佳成像位置处于两相机传感器平面的同侧，式(3)所适用条件为颗粒的最佳成像位置处于两相机传感器平面的中间。所以，只需获得2张粒子离焦图像的模糊半径比即可采用式(2)或式(3)对运动颗粒进行空间定位。

图2所示为同一颗粒相同物距时在不同成像面上获得的离焦半径不同的2幅图像M1和M2，先利用均值滤波对其进行去噪处理，然后采用梯度算法得到灰度梯度图像，再利用最大类间差法获取梯度图像的阈值，并采用该阈值对梯度图像进行二值化，得到最终处理结果如图2中N1和N2所示。

(a) 离焦程度较小的图像M1；(b) 离焦程度较大的图像M2；(c) M1的处理结果N1；(d) M2的处理结果N2

定义2幅梯度图像边缘过渡区面积分别为1和2，随着图像由聚焦图像逐渐模糊，由小变大，由图像矩不变原理[16]，与图像的离焦半径成正比，即

其中：为常数，则有

代入式(2)或式(3)即可得到目标的物距，实现颗粒的空间定位。

1.3 离焦二义性判定

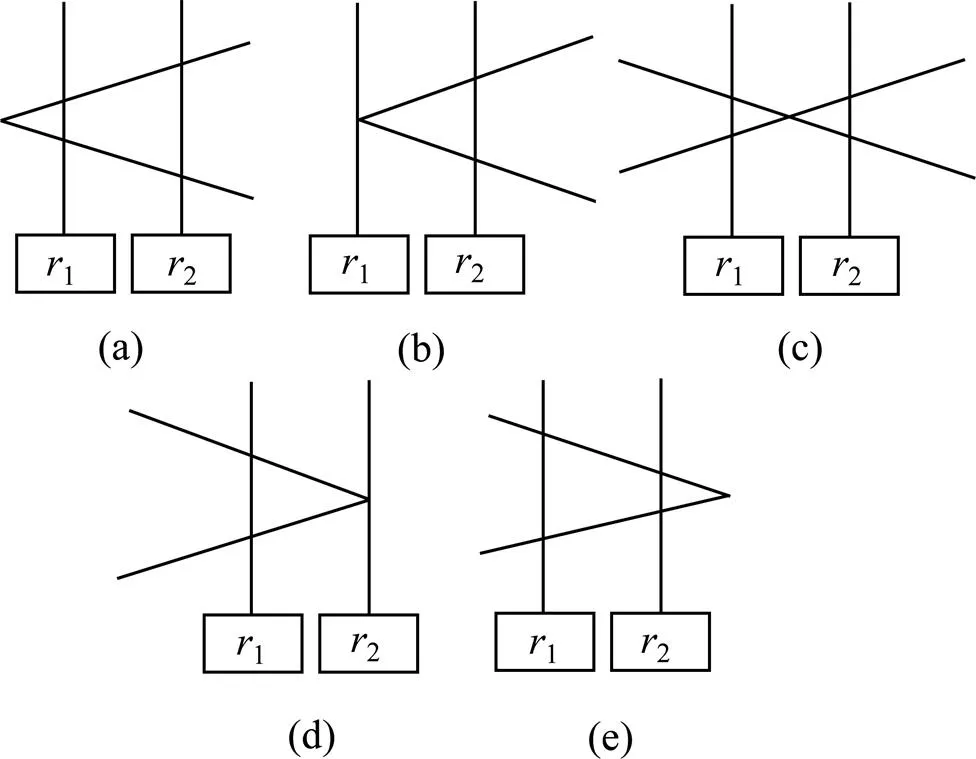
(a); (b); (c); (d) ; (e)

对于图3(a)和图3(e)所示2种情况，应采用式(2)计算物距，对图3(c)所示情况则应采用式(3)来计算。图3(b)与图3(d)所示为2种临界情况，此时清晰成像面分别与成像平面D1与D2重合。当清晰成像面与成像平面D1重合即1=0时，物点在成像平面D2上成像的弥散圆半径记为，根据图1中的几何关系可得到其计算公式为

同理，当2=0时，物点在成像平面D1上成像的弥散圆半径为

其中：为远心镜头物方焦点处的光阑直径。

在实际测量过程中，对相机1拍摄获得的图像进行处理，若其离焦半径小于，且相机2上对应图像的离焦半径小于，即对应图3(c)所示的情况，则采用式(3)进行计算，否则采用式(2)。由此可解决模糊图像的离焦二义性问题。

2 单镜头双相机运动颗粒三维定位系统

本文作者研制的单镜头双相机运动颗粒三维定位系统示意图如图4所示，系统使用LED光源以背光方式照明测量区域中的运动颗粒，光线经镜头收集后被半透半反分光棱镜分成光强相同的2束，分别进入2个相机，实现双相机从同一视场方向对颗粒进行成像。其中相机1与分光棱镜的距离保持不变，即1不变，相机2与分光棱镜之间的距离可以通过添加接圈进行调节。采用信号发生器实现两相机的同步触发，对同一时刻拍摄到的相同颗粒不同离焦模糊程度的图像进行处理，从而获得运动颗粒的三维位置信息。

图4 单镜头双相机系统示意图

初步试验结果表明：两相机与分光棱镜之间距离的差别(即2−1)过小时2幅图像模糊度差别不明显，过大则测量区域变化较大，最适宜的像距差值随镜头参数的变化将有所不同。经尝试性试验发现，本装置在该差值为5 mm左右时可获得成像模糊度差值较明显且测量区域接近的2幅图像。考虑到实验室现有的接圈尺寸，本文试验中选择双相机对应的像距差值为 4.2 mm。光学成像系统的其他光学参数及几何长度的物理示意图如图5所示，图5中，为焦距，1为镜头长度，2为镜头前端面到前主平面距离，3为镜头前端面到后主平面距离，4为分光棱镜光路长度，5为分光棱镜到相机1成像平面距离，6为分光棱镜到相机2成像平面的距离。

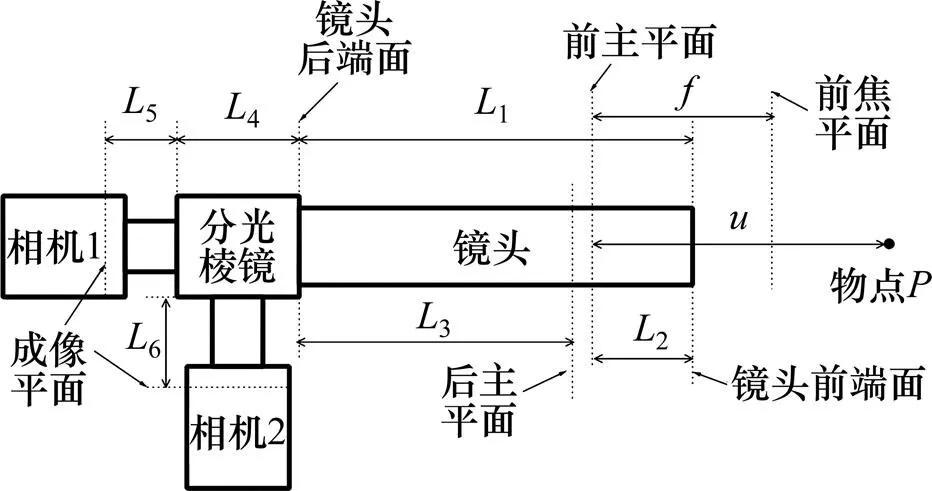
图5 系统光学参数示意图

图5所示参数的具体数值如表1所示，由此可计算出镜头后主平面到相机1和相机2成像平面的距离1和2，分别为264.4 mm和268.6 mm。

表1 系统光学参数数值

3 单镜头双相机系统离焦测距试验

3.1 圆点标定板离焦测距试验

为验证上述系统与处理算法的可行性，采用此装置对圆点标定板进行离焦测距试验。图6所示为圆点标定板在4组不同距离时2个相机分别获得的离焦图像，利用第1节所述原理对4组图像进行分析，得到粒子与镜头前端面距离，如表2所示。与真实值相比较可见测量结果变化趋势合理，其相对误差在10%以内。分析误差发现：1) 由于本装置中镜头的像方远心度不为0°，导致不同成像平面上成像大小发生变 化，使测量结果产生一定偏差，若选用物像双侧远心镜头有望进一步提高测量精度；2) 在提取颗粒过渡区面积时，采用OTSU法获得的梯度图像阈值易受图像大小及图像整体对比度的影响，需要进一步深入考虑；3) 通过理论分析发现，在本文的测量条件下，算法的计算精度为5%左右；4) 在计算2张图像模糊半径的比值时，只利用了图像的边缘宽度信息，而忽略了模糊图像边缘灰度信息[17]，在后续研究中应进行考虑，以实现模糊半径的更精确测量。

u/mm：(a) 39.80；(b) 40.50；(c) 41.00；(d) 42.00

表2 静止圆点离焦测距

3.2 运动颗粒离焦测距试验

为验证该方法对运动颗粒测距的可行性，对上升过程中的电解食盐水气泡进行拍摄，获得如图7所示的2张含不同大小和位置的气泡图片。从图7可见有3种位置情况下的颗粒图像，正方形框中的颗粒在相机2中的成像比在相机1中的成像清晰，椭圆形框中颗粒成像模糊度相反，而菱形框中颗粒在相机1与相机2上成像模糊度相近。由于实验装置中1＜2，即相机2的成像平面距离镜头较远，其拍摄到的图像中最清晰粒子位置到镜头前端距离应较近。故重构正方形与椭圆形框中粒子空间位置时应使用式(2)，而重构菱形框中粒子空间位置时应使用式(3)。基于上述判断，重构气泡三维空间深度信息，如图8所示。以镜头前端面为基准面，所识别出的气泡深度为0.90 mm，与实际产生电解食盐水气泡的铜丝所得深度1.07 mm较符合，证明了该测量方法和装置的可行性。

(a) 相机1采集的离焦图像；(b) 相机2采集的离焦图像

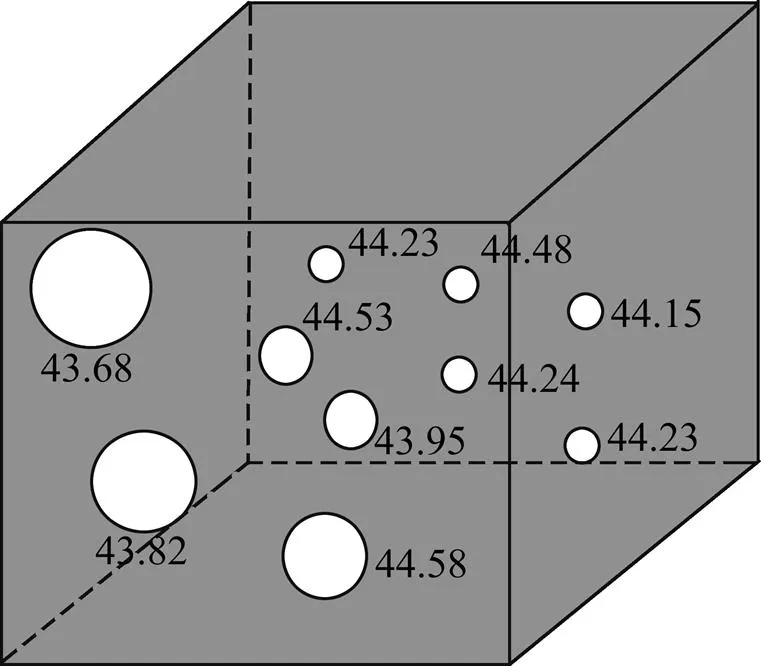
图8 运动气泡空间位置重构

4 结论

1) 基于单镜头双相机的离焦测距方法和装置解决了模糊图像的离焦二义性问题，可以实现运动颗粒在无参照物情况下的三维定位。

2) 本试验条件下对静止颗粒的离焦测距试验相对误差在10%以内，并实现了运动气泡的三维定位，证明了测量方法和装置的可行性，为颗粒的多参数三维场测量奠定了基础。

3) 该测量装置采用1个镜头和2个相机，保证拍摄视角的一致性，避免了双目视觉中空间点匹配问题，算法简单；若将分光棱镜和2个图像传感器集成，即形成1个双图像传感器相机，则装置及操作会更为 简便。

[1] 刘友, 杨晓涛, 马修真. 基于激光多普勒测速的流场测试技术[J]. 激光与红外, 2012, 42(1): 18−21. LIU You, YANG Xiaotao, MA Xiuzhen. Technique of flow field measurement based on laser Doppler velocimetry[J]. Laser and Infrared, 2012, 42(1): 18−21.

[2] 张晓艳. 平面二维瞬时流速场数字图像测速技术研究[D]. 太原: 太原理工大学水利科学与工程学院, 2005: 4−10. ZHANG Xiaoyan. Study of digital image velocimetry for simultaneous flow field in two dimensional plane[D]. Taiyuan: Taiyuan University of Technology. School of Water Conservancy Science and Engineering, 2005: 4−10.

[3] 沈熊. 激光测速技术(LDV)诞生50周年启示[J]. 实验流体力学, 2014, 28(6): 51−55. SHEN Xiong. A historical review for the 50th anniversary of laser doppler velocimetry[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(6): 51−55.

[4] 贾卫东, 李萍萍, 邱白晶, 等. PDPA 在喷嘴雾化特性试验研究中的应用[J]. 中国农村水利水电, 2008(9): 70−72. JIA Weidong, LI Pingping, QIU Baijing, et al. Application of phase doppler particle analyzer in reek spray nozzle’s characteristic experiment[J]. China Rural Water and Hydropower, 2008(9): 70−72.

[5] KASHDAN J T, SHRIMPTON J S, WHYBREW A. A digital image analysis technique for quantitative characterisation of high-speed sprays[J]. Optics and Lasers in Engineering, 2007, 45(1): 106−115.

[6] 王建华, 冯帆, 梁伟, 等. 双目立体视觉测量系统的设计与实现[J]. 舰船电子工程, 2012, 32(4): 107−109. WANG Jianhua, FENG Fan, LIANG Wei, et al. Design and implementation of measurement system based on binocular stereo vision[J]. Ship Electronic Engineering, 2012, 32(4): 107−109.

[7] 申功炘,张永刚,曹晓光,等. 数字全息粒子图像测速技术(DHPIV)研究进展[J]. 力学进展, 2007, 37(4): 563−574. SHEN Gongxin, ZHANG Yonggang, CAO Xiaoguang, et al. Advances in DHPIV[J]. Advances in Mechanics, 2007, 37(4): 563−574.

[8] CHEN Xiaozhen, ZHOU Wu, CAI Xiaoshu, et al. In-line imaging measurements of particle size, velocity and concentration in a particulate two-phase flow[J]. Particuology, 2014, 13(1): 106−113.

[9] 周烨锋, 邱慧娟, 李卓. 基于远心光学系统散焦图像的距离估计[J]. 红外与激光工程, 2006, 35(Suppl): 534−537. ZHOU Yefeng, QIU Huijuan, LI Zhuo. Depth estimation based on defocus image of the telecentric lens[J]. Infrared and Laser Engineering, 2006, 35(Suppl): 534−537.

[10] 程鸿, 章权兵, 宫炎焱. 一种新的基于散焦图像的深度恢复算法[J]. 计算机应用与软件, 2010, 27(2): 271−273. CHENG Hong, ZHANG Quanbing, GONG Yanyan. A new depth recovery algorithm based on defocus image[J]. Computer Applications and Software, 2010, 27(2): 271−273.

[11] BAILEY S W, ECHEVARRIA J I, BODENHEIMER B, et al. Fast depth from defocus from focal stacks[J]. Visual Computer, 2015, 31(12): 1697−1708.

[12] LEE E, CHAE E, CHEONG H, et al. Depth-based defocus map estimation using off-axis apertures[J]. Optics Express, 2015, 23(17): 21958−21971.

[13] PENTLAND A P. A new sense for depth of field[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(4): 523−531.

[14] ZHOU C, NAYAR S. What are good apertures for defocus deblurring?[C]// Proceedings of IEEE International Conference on Computational Photography. San Francisco, USA: IEEE, 2009: 1−8.

[15] 田涛, 潘俊民. 基于矩保持法的散集图像深度估计[J]. 上海交通大学学报, 2000, 34(7): 917−920. TIAN Tao, PAN Junmin. Depth estimation from defocus based on moment-preserving[J]. Journal of Shanghai Jiaotong University, 2000, 34(7): 917−920.

[16] KUNDUR D, HATZINAKOS D. Blind image deconvolution[J]. Signal Processing Magazine, IEEE, 1996, 13(3): 43−64.

[17] 张仕玲, 孙旭. 基于 Matlab 的图像清晰度评价方法研究[J]. 通信技术, 2012, 44(12): 7−9. ZHANG Shiling, SUN Xu. Image evaluation based on east wavelet transform[J]. Communications Technology, 2012, 44(12): 7−9.

Method of three-dimensional positioning for moving particles with single lens

JIN Na, ZHOU Wu, HU Jiarui, CAI Xiaoshu

(Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

Based on the optical principles of depth from defocus(DFD), a method with a single lens and two image sensors was proposed to determine the three-dimensional positions of moving particles and an imaging system was established for measurement of particle locations. The theoretical and experimental analyses were carried out to explore the relationship between defocus blur degree of image and particle depth. A dispersion prism was used to connect a lens and two cameras, and synchronous measurement was realized with a signal generator. Two images with different defocus blur degrees could be captured for the same particle by adjusting the distances between the two image sensors and the lens. The depth information could be extracted from these two images. The distance difference between two image sensors and the lens was adopted as 4.2 mm. The validation experiments of the measurement system were carried out using static particles, in which the relative measurement errors were within 10%. And the three-dimensional defocus distance test was carried out for bubbles produced by electrolysis of salt water using the system. The results show that this method well feasible, and the problem of position blur in DFD with single lens can be solved using this setup, which indicates that DFD without

can be realized.

moving particles; single-lens double-camera; depth from defocus; spatial orientation; ambiguity of defocus

10.11817/j.issn.1672-7207.2016.09.045

TH7

A

1672−7207(2016)09−3246−06

2015−09−07；

2015−11−25

国家自然科学基金资助项目(51206112，51327803)；上海市自然科学基金资助项目(12ZR1446900)；上海市教委科研创新项目(12YZ110) (Projects(51206112, 51327803) supported by the National Natural Science Foundation of China; Project(12ZR1446900) supported by the Natural Science Foundation of Shanghai Municipality; Project(12YZ110) supported by the Innovation Project of Scientific Research of Shanghai Municipal Education Commission)

周骛，博士，副教授，从事颗粒与流场在线测量方法研究；E-mail: zhouwu@usst.edu.cn

(编辑 刘锦伟)