预应力影响下混凝土结构锈胀开裂计算

张建仁，戴理朝，张旭辉，王磊



预应力影响下混凝土结构锈胀开裂计算

张建仁，戴理朝，张旭辉，王磊

(长沙理工大学土木与建筑学院，湖南长沙，410114)

针对预应力钢绞线腐蚀引起混凝土结构锈胀开裂问题，考虑混凝土双向应力状态和钢绞线截面几何特性等因素的影响，建立微裂缝形成、保护层开裂及开裂至一定宽度的锈胀开裂3阶段计算模型，分析锈胀开裂对预应力等各影响因素的敏感性，并通过试验对理论结果进行验证。研究结果表明：预应力会对锈胀开裂产生不利影响，与无应力状态相比，当钢绞线预应力为75%的抗拉强度标准值时，微裂缝形成、保护层开裂和开裂至0.1 mm时的腐蚀率分别降低了46.14%，43.90%和9.42%；锈胀发展3阶段的腐蚀率均随铁锈膨胀率和钢绞线直径的增加而减小，随混凝土抗拉强度和保护层的增加而增大。

桥梁工程；锈胀开裂；预应力钢绞线；腐蚀；双向应力状态

在高应力与侵蚀环境耦合作用下，混凝土结构中的预应力筋比普通钢筋更易被腐蚀。腐蚀产物体积膨胀会导致混凝土保护层开裂，即所谓的锈胀开裂[1]。锈胀裂缝的出现又会进一步为有害物质进入结构内部提供通道，进而加快预应力筋的腐蚀，造成结构性能的提早退化，大大影响结构耐久性[2]。因此，保护层锈胀开裂作为混凝土结构耐久性极限状态的标志，明确其开裂机理，建立其预测模型具有重要的理论和工程意义。锈蚀膨胀对混凝土结构耐久性极其不利。为此，国内外学者对钢筋混凝土(RC)锈胀问题开展了大量试验和理论研究。锈胀试验研究多采用电化学快速腐蚀的方法，研究锈胀裂缝开展随腐蚀率的变化规 律[3]。目前，在锈胀开裂的影响因素等方面已经取得了大量成果，发现开裂临界时间随混凝土强度、保护层厚度的增加而增大，会随钢筋直径的增大而降 低[3−4]。在理论研究方面，针对均匀腐蚀，一些学者将锈胀作用模拟为环状受力状态，以弹性力学或断裂力学为基础，建立了锈胀开裂预测模型[5−7]。对于局部坑蚀，一些学者将钢筋腐蚀后的截面假定为椭圆形，基于厚壁圆筒理论发展了锈胀开裂模型[8]。另外，在基于有限元方法的锈胀开裂模拟方面，也取得了一些成果[9−11]。研究发现，开裂时局部腐蚀所需的锈胀力比均匀腐蚀所需的锈胀力小[9]；非均质模型相对均质模型而言，能更真实地模拟保护层的开裂和失效模式[10]。但需要指出的是，现有研究均是针对普通钢筋混凝土的锈胀开裂，预应力构件的锈胀开裂问题鲜有报道。在预应力混凝土(PC)结构中，预应力筋长期处于高应力状态，侵蚀环境下其腐蚀速率比普通钢筋的大。再者，通常预应力筋直径较大，这使其腐蚀更易导致结构锈胀开裂[12−14]。与普通RC构件类似，预应力混凝土锈胀开裂也可大致分为3个阶段：微裂缝形成、保护层开始开裂、锈胀到一定宽度。但预应力混凝土锈胀开裂更为复杂，主要表现在以下2点：混凝土处于双向应力状态，即横向锈胀力和纵向预应力，预应力的存在会改变混凝土开裂时所需的锈胀力；再者，混凝土结构中预应力钢绞线由多根钢丝捻制而成，其横截面形状更为复杂，这增加了其截面损失率的计算难度。现有文献调研表明，考虑以上因素对预应力混凝土锈胀开裂影响的研究尚未见报道。为此，本文作者针对预应力混凝土结构，考虑混凝土双向应力状态和预应力筋截面几何效应影响，推导保护层锈胀开裂各阶段腐蚀率的计算模型，发展PC结构锈胀开裂全过程的计算方法，通过试验对该模型进行验证，并分析预应力、保护层厚度、混凝土抗拉强度、预应力筋直径和铁锈膨胀率等参数对锈胀开裂的影响，明确锈胀开裂对各参数的敏感性。

1 微裂缝形成时临界腐蚀率

如前所述，在PC结构中，预应力筋周围混凝土除受横向腐蚀产物引起的锈胀力外，还受纵向预应力的约束作用。另外，工程中的钢绞线为多根钢丝捻制而成，其截面形态多与普通钢筋的形态不同。因此，锈胀分析时要考虑这2个因素。

混凝土是非均质材料，内部多存在较小的孔隙。钢绞线开始被腐蚀后，产生的腐蚀产物首先用于填入交界面混凝土的孔隙，为简化分析，此阶段填充孔隙造成的腐蚀率忽略不计。当腐蚀产物填充完交界面混凝土的孔隙后，钢绞线周围混凝土才会受到拉应力作用，产生微裂缝。以桥梁常用的7根钢丝捻制而成的钢绞线为对象，对保护层厚度为的PC结构，图1所示为钢绞线及其周围混凝土受力状况。其中：为保护层厚度；为交界面处锈胀应力；为混凝土内部任意位置到钢铰线重心的距离；t为混凝土环向应力；()为混凝土的预压应力；为最大锈胀应力处微裂缝端部至钢绞线重心的距离；0为单根钢丝的初始半径。当锈胀应力产生的环向拉应力等于双向应力状态下混凝土的主拉应力时，会产生微裂缝。

(a) 半剖面图；(b) 半横断面图

在单元体中，混凝土处于双向应力状态，即纵向受到预压应力，横向受到锈胀应力产生的拉应力。预应力作用下，钢绞线位置处混凝土的预压应力为

式中：p为钢绞线的预压应力；为构件截面面积；为构件截面惯性矩；p为钢绞线重心至中和轴的距离。

除预压应力外，混凝土还受环向应力的作用。由图1(b)可知：根据应力的等效分布原理，微裂缝端部处的锈胀应力Q为

双向应力状态下的混凝土，双向应力存在如下关系[15]：

将式(1)~(3)代入式(4)得到锈胀应力的表达式。对其求导，可得=0.486(+30)。进而得混凝土微裂缝形成时最大锈胀应力为

对于桥梁常见的由7根钢丝捻制的钢绞线而言，钢绞线与混凝土的接触面只有外围的6根钢丝，外围钢丝与混凝土的接触面占单根钢丝周长的2/3，如图2所示。图2中：c为腐蚀后膨胀半径；ρ为腐蚀后净半径；1为交界面处混凝土径向位移；2为交界面处铁锈径向位移；为单根钢丝的初始直径。对同一结构，以相同直径的钢绞线和普通钢筋为分析对象，由于外围钢丝与混凝土的接触面占单根钢丝周长的2/3，钢绞线与混凝土交界面的周长比普通钢筋的周长大。交界面处预应力筋与混凝土的接触面积越大其腐蚀速率越快，腐蚀速率越快则结构锈胀开裂所需的时间越短[3]。

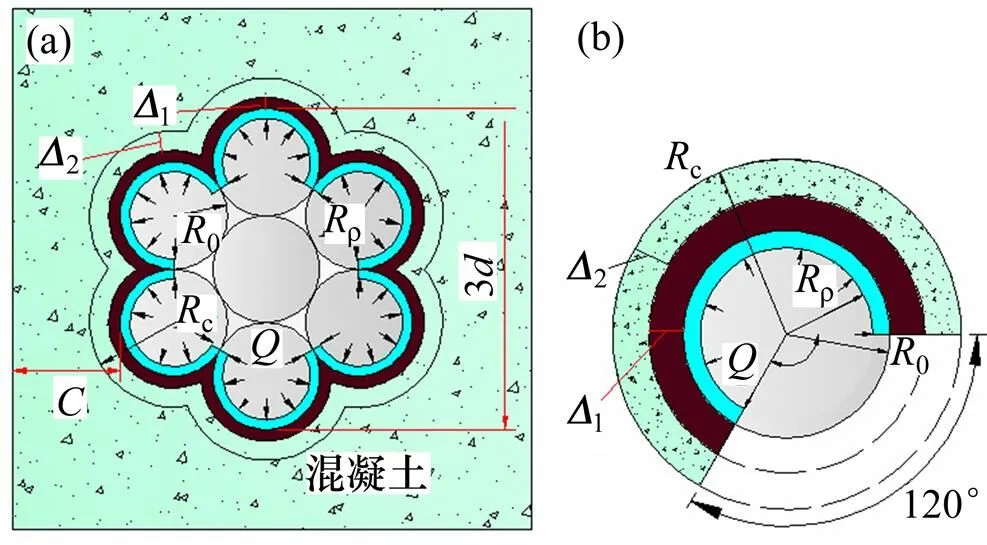
(a) 锈蚀产物引起变形；(b) 单根钢丝锈胀放大

当钢绞线受侵蚀物质腐蚀时，外围钢丝与混凝土接触面会先发生腐蚀，即单根钢丝2/3表面先发生腐蚀。由于钢绞线截面的复杂性，相对普通钢筋而言，其腐蚀率与截面积减小量之间的计算也更为复杂。通过钢绞线截面面积减小量和腐蚀率之间关系，可得三者关系如下：

式中：为铁锈体积膨胀率，通常为2~4[5]；p为未腐蚀钢绞线截面面积；m为微裂缝形成时临界腐蚀率。

当混凝土内部产生微裂缝时，交界面处混凝土受到钢绞线锈胀力作用会产生1的变形，铁锈受锈胀力作用的变形为2，如图2所示。

根据环状轴对称应力结构的应力分布特点，钢绞线与混凝土交界面处的锈胀应力为，混凝土保护层表面锈胀应力为0 Pa[5]。可得到在锈胀力作用下，交界面处混凝土的径向位移1表达式为

式中：c和c分别为混凝土的弹性模量和泊松比。

根据环状轴对称应力结构的应力和位移边界条件，膨胀半径处的径向应力为，腐蚀后净半径处的径向位移为0 mm[5]。得到交界面处铁锈的径向位移2为

式中：r和r分别为铁锈的弹性模量(N/mm2)和泊松比，文献[16]中r=0.49，r=6 000(1−2r)。

图2中钢绞线与混凝土的交界面满足变形协调关系，钢丝初始半径0加上混凝土的径向位移1等于钢丝腐蚀后的膨胀半径c减去铁锈的径向位移2。由变形协调方程得

由式(6)知c为m的函数，将式(10)中的m用c表示，联立式(5)和式(10)，得到c的一元三次方程为

；

；

。

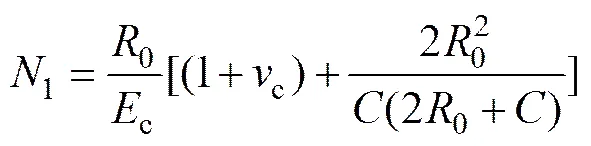
求解上式得c的表达式，将c代入式(6)求得m，进而得微裂缝形成时单根钢丝腐蚀深度m表达式。

2 保护层开裂时临界腐蚀率

随着腐蚀程度的增加，腐蚀产物的进一步增多导致保护层表面出现开裂。混凝土作为脆性材料，当锈胀产生的拉应力超过混凝土的抗拉强度时，混凝土内部会产生裂缝。钢绞线与混凝土交界面处裂缝宽度与填入裂缝的铁锈体积c直接相关。铁锈体积c又取决于腐蚀深度p和临界腐蚀率p。

由上分析可知，微裂缝形成时单根钢丝腐蚀深度为m，钢绞线与混凝土交界面处铁锈的半径增量为(−1)m。假定钢绞线和混凝土交界面处裂缝的宽度产生是由铁锈膨胀导致交界面处混凝土周长增加所造成的[5]，如图3所示。钢绞线与混凝土交界面处裂缝宽度w之和为

保护层开裂时混凝土内部裂缝的开展如图3所示。将裂缝分布近似等效为三角形，且裂缝长度延伸至保护层表面，可得单位长度内填入裂缝中铁锈体积。由于腐蚀产物产生的锈胀力会使混凝土开裂，进而使铁锈填充裂缝。根据钢绞线锈蚀深度与铁锈体积之间的关系，得到保护层开裂时钢绞线腐蚀深度p的表达式为

当钢绞线受到侵蚀时，外围钢丝先被腐蚀，可得到保护层开裂时的临界腐蚀率p与p之间的关系为

综上所述，将c代入式(13)得到p，再将p代入式(14)即可求得保护层开裂时临界腐蚀率。

3 保护层开裂至一定宽度时的腐蚀率

当腐蚀率超过保护层锈胀开裂临界腐蚀率时，保护层表面即开始出现可见锈胀裂缝。锈胀裂缝加宽后，在横截面方向，裂缝的形状由三角形向长方形发展，如图4所示。

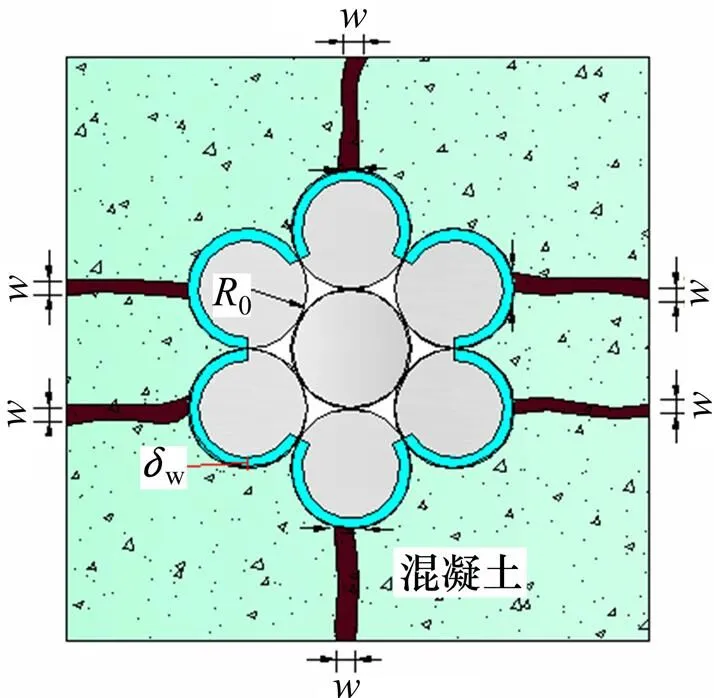
图4 锈胀裂缝宽度与腐蚀率之间的关系

此时，锈胀裂缝宽度与钢绞线腐蚀深度w之间的关系为

锈胀裂缝宽度对应的腐蚀率w与w之间的关系为

将式(15)代入式(16)得w与之间的关系为

这样即可根据锈胀裂缝的检测宽度来推算其对应的腐蚀率。

4 锈胀开裂模型的试验验证

试验设计制作了8片不同预应力筋腐蚀程度的后张PC梁，试验梁的截面长×高×宽为2 000 mm× 220 mm×150 mm。混凝土轴心抗压强度实测值cd=31.8 MPa。预应力筋采用直径为15.2 mm的7丝钢绞线，其屈服强度为1 830 MPa，极限强度为1 910 MPa，控制张拉荷载为194 kN，预应力筋重心至梁下边缘距离为60 mm。预留直径为32 mm的预应力筋孔洞，预留孔洞采用橡胶棒拉拔成孔，孔道压浆材料为水泥浆，其水灰比为0.4。梁尺寸及配筋图如图5所示。

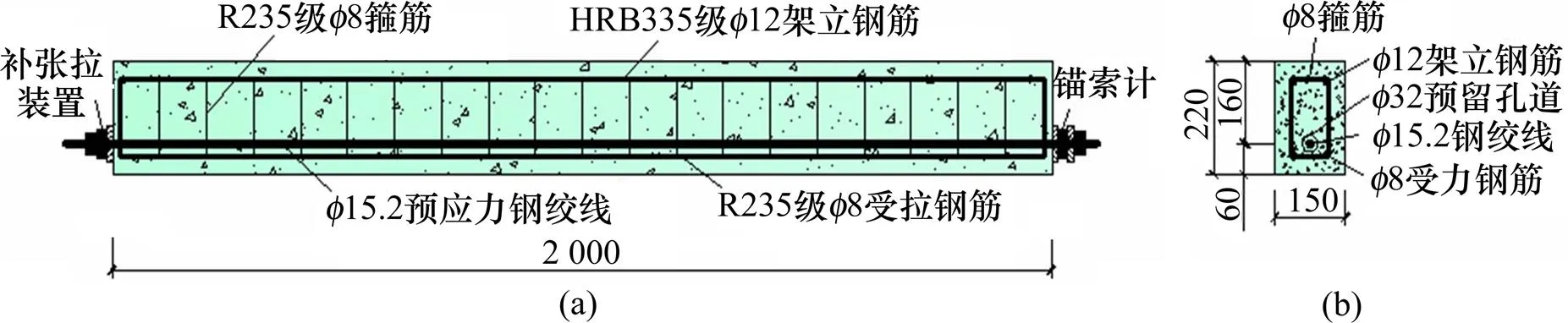
(a) 试验梁尺寸；(b) 截面尺寸单位：mm

试验采用电化学快速腐蚀法对试件内的预应力筋进行加速腐蚀。为单独研究预应力筋腐蚀的影响，利用环氧树脂对所有普通钢筋进行防腐处理，保证普通钢筋不被腐蚀。将试验梁浸泡在质量分数为10%的NaCl溶液中，恒定直流电源的阳极与试验梁的预应力筋连接，阴极与腐蚀溶液中的不锈钢连接，通过腐蚀槽中的NaCl溶液形成电流闭合回路。在电流作用下，阳极预应力筋释放出的电子被氧化，从而导致预应力筋被腐蚀。

为明确预应力筋腐蚀与锈胀裂缝之间的关系，试验梁加速腐蚀后，对试验梁表面的锈胀裂缝进行测量，试验梁的两侧和底面分别标记为A~C。各腐蚀梁3个面预应力筋位置处均出现了锈胀裂缝，典型锈胀裂缝的开展情况如图6所示。

(a) A面；(b) B面；(c) C面

选取其中5片平均腐蚀率较低的试验梁作为研究对象。沿纵向梁长方向每隔10 cm测量一次锈胀裂缝的宽度。表1所示为各试验梁锈胀裂缝宽度试验值与理论值。水泥浆与普通混凝土材料力学特性存在差异性，为简化分析，理论模型将水泥浆和混凝土假定为同一种材料。现有研究表明铁锈膨胀率通常为2~4[5]，本文基于现有文献研究成果取为平均值3。表1所示平均腐蚀率为质量腐蚀率，试验梁A和B面的保护层厚度相同，为便于分析，当保护层厚度为67.4 mm时，平均锈胀裂缝宽度取为梁长方向A和B面锈胀裂缝宽度的平均值，当保护层厚度为52.4 mm时，平均锈胀裂缝宽度取梁长方向C面锈胀裂缝宽度的平均值。

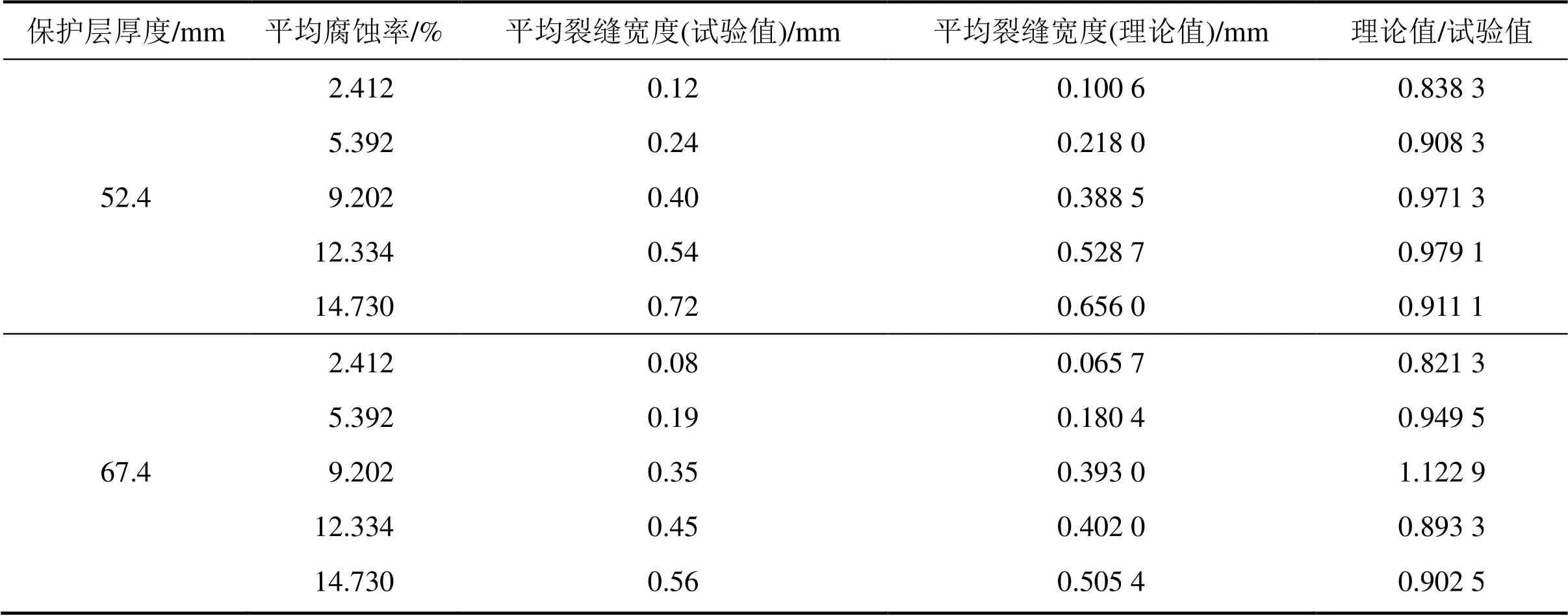
表1 平均锈胀裂缝宽度试验值与理论值的比较

结合本文锈胀至一定宽度腐蚀率计算模型，对试验梁锈胀裂缝宽度进行了理论分析。保护层厚度为52.4 mm的面，理论值与试验值的最大相对误差为16.17%，平均相对误差为7.84%；当保护层厚度为67.4 mm时，理论值与试验值的最大相对误差为17.87%，平均相对误差为6.21%。理论值和试验值存在一定误差，这是混凝土强度不确定性以及预应力筋腐蚀率和裂缝宽度测量过程中存在误差等原因造成的，整体上理论值与试验值误差是可以接受的。

试验过程中直接测量保护层开裂时的临界腐蚀率十分困难。文献[3]研究表明：当腐蚀率不大时，锈胀裂缝宽度随腐蚀率的增大呈线性增长。为此，保护层开裂时临界腐蚀率可通过试验值拟合得到。平均锈胀裂缝宽度与平均腐蚀率之间的关系如图7所示。

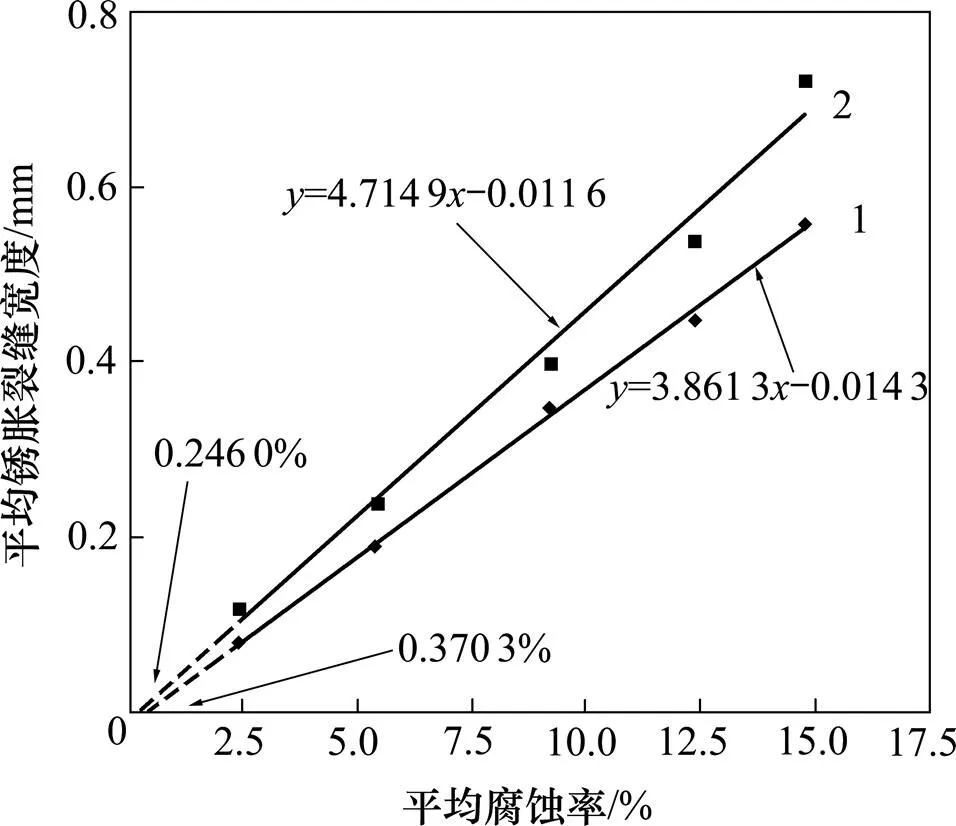
保护层厚度/mm：1—67.4；2—52.4。

由图7可知：当保护层厚度为52.4 mm时，保护层开裂时临界腐蚀率的试验值为0.246 0%，而相应的理论值为0.275 8%，相对误差为12.11%；当保护层厚度为67.4 mm时，保护层开裂时临界腐蚀率的试验值为0.370 3%，理论值为0.407 2%，相对误差为9.97%。理论值与试验值相对误差可以接受。

以上2个方面的试验验证了该理论模型的适用性，可以有效计算预应力混凝土锈胀开裂。

5 各阶段腐蚀率的影响因素

锈胀开裂受预应力、混凝土抗拉强度、保护层厚度、铁锈膨胀率和钢绞线直径等因素的影响。

5.1 预应力的影响

以本文试验梁为分析对象，取铁锈膨胀率为3.0，研究微裂缝形成、保护层开裂和开裂至一定宽度时腐蚀率随预应力的变化，如图8所示。

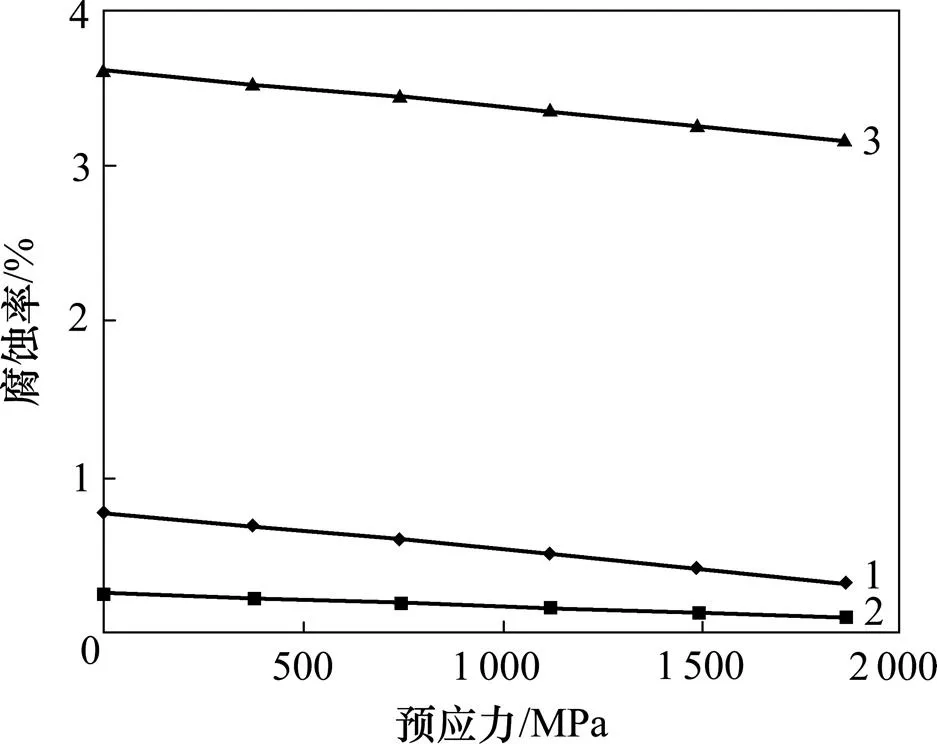
1—保护层开裂时临界腐蚀率ρp；2—微裂缝形成时临界腐蚀率ρm；3—保护层开裂至0.1 mm时的腐蚀率ρw。

由图8可知：微裂缝形成、保护层开裂以及保护层开裂至0.1 mm时腐蚀率均随预应力的增加而降低。JTG D62—2004“公路钢筋混凝土及预应力混凝土桥涵设计规范”规定[17]：钢铰线的张拉控制应力应小于75%的抗拉强度标准值。与无应力状态相比，钢绞线预应力在75%的抗拉强度标准值时，微裂缝形成、保护层开裂和开裂至0.1 mm时的腐蚀率分别降低了46.14%，43.90%和9.42%。当预应力取0 MPa时，其值为RC结构的临界腐蚀率。这表明，侵蚀环境下PC结构比RC结构更易导致锈胀开裂。

5.2 混凝土抗拉强度和铁锈膨胀率的影响

同样，以本文试验梁为研究对象，腐蚀率对混凝土抗拉强度和铁锈膨胀率的敏感性如图9所示。

图9 混凝土抗拉强度和铁锈膨胀率对腐蚀率的影响

微裂缝形成时临界腐蚀率、保护层开裂时临界腐蚀率和开裂至0.1 mm时腐蚀率随混凝土抗拉强度的增加而增大，随铁锈膨胀率的增加而减小。铁锈膨胀率对开裂前和开裂后腐蚀率均有较大影响；而混凝土抗拉强度仅对保护层开裂前有较大影响，提高混凝土抗拉强度对锈胀开裂后的影响不大。

5.3 混凝土保护层和钢绞线直径的影响

依旧以本文试验梁为对象，取铁锈膨胀率为3.0，分析保护层厚度和钢绞线直径对腐蚀率的影响，如图10所示。

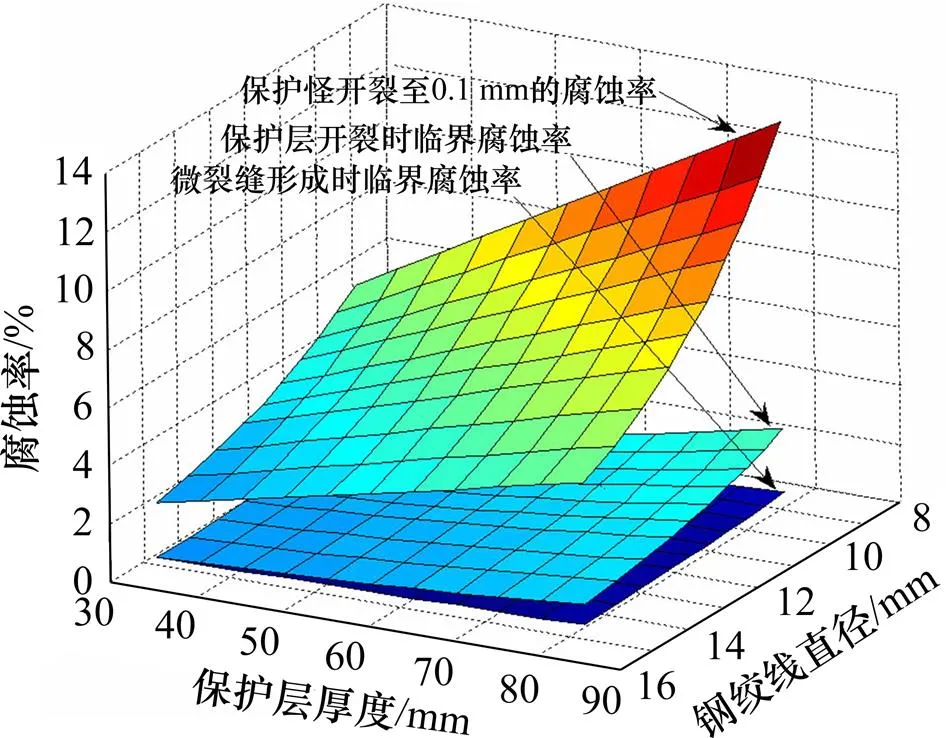
图10 保护层厚度和钢绞线直径对腐蚀率的影响

3种情况下，腐蚀率均随保护层厚度的增加而增大，随钢绞线直径的增大而减小。降低钢绞线直径和提高保护层厚度对混凝土保护层开裂前和开裂后的影响均有较明显的作用。提高混凝土保护层厚度和采用小直径的钢绞线能有效延缓锈胀裂缝的开展。在3个腐蚀率中，混凝土开裂至一定宽度的临界腐蚀率对保护层厚度和钢筋直径更为敏感。

6 结论

1)在预应力混凝土锈胀开裂计算过程中，应有效考虑预应力的影响。预应力筋的预加力作用会对锈胀裂缝产生不利影响，锈胀开裂的临界腐蚀率随预应力的增大而减小。与无应力状态相比，钢绞线预应力在75%的抗拉强度标准值时，微裂缝形成、保护层开裂和开裂至0.1 mm时的腐蚀率分别降低了46.14%，43.90%和9.42%。

2) 在相同直径条件下，捻制而成的钢绞线与混凝土交界面的周长较普通钢筋的周长大。

3) 微裂缝形成、保护层开裂及开裂至一定宽度时腐蚀率均随混凝土抗拉强度和保护层厚度的增加而增大，随铁锈膨胀率和钢绞线直径的增加而减小。

4) 采用厚保护层、小直径钢绞线以及高强度混凝土等措施，对延迟PC结构的锈胀开裂有较好的作用。

5) 该模型可以有效计算PC结构的锈胀开裂，误差在可接受范围内。但需要指出的是，本文对腐蚀PC结构锈胀开裂进行受力分析时，假定混凝土为理想弹性体，而混凝土材料本身为非理想弹性体。如何准确地考虑混凝土材料性能和腐蚀产物对锈胀开裂的影响尚需深入研究。

[1] CASTEL A, CORONELLI D, VU N A, et al. Structural response of corroded, unbonded posttensioned beams[J]. Journal of Structural Engineering, 2011, 137(7): 761−771.

[2] CHERNIN L, VAL D V. Prediction of corrosion-induced cover cracking in reinforced concrete structures[J]. Construction and Building Materials, 2011, 25(4): 1854−1869.

[3] 王显利, 郑建军. 钢筋混凝土结构锈胀开裂及裂缝扩展试验研究[J]. 大连理工大学学报, 2009, 49(2): 246−252. WANG Xianli, ZHENG Jianjun. Experimental study of corrosion-induced crack initiation and propagation of reinforced concrete structures[J].Journal of Dalian University of Technology, 2009, 49(2): 246−252.

[4] AMIN J, UELI A, BRYAN A, et al. Modeling of corrosion- induced concrete cover cracking: a critical analysis[J]. Construction and Building Materials, 2013, 42(5): 225−237.

[5] 赵羽习, 金伟良. 钢筋锈蚀导致混凝土构件保护层开裂的全过程分析[J]. 水利学报, 2005, 36(8): 939−945. ZHAO Yuxi, JIN Weiliang. Anslysis on cracking of concrete cover due to corrosion[J].Journal of Hydraulic Engineering, 2005, 36(8): 939−945.

[6] 赵羽习. 钢筋锈蚀引起混凝土结构锈裂综述[J]. 东南大学学报, 2013, 43(5): 1122−1134. ZHAO Yuxi. State-of-art of corrosion-induced cracking of reinforced concrete structures[J]. Journal of Southeast University, 2013, 43(5): 1122−1134.

[7] CAO C, CHEUNG M M S, CHAN B Y B. Modelling of interaction between corrosion-induced concrete cover crack and steel corrosion rate[J]. Corrosion Science, 2013, 69(1): 97−109.

[8] GOITSEONE M, MARK A, PILATE M. Model for cover cracking of RC beams due to partial surface steel corrosion[J]. Construction and Building Materials, 2011, 25(2): 987−991.

[9] BRANKO S, MLADENA L, JOSE P, et al. Cracking of the concrete cover due to reinforcement corrosion: a two- dimensional lattice model study[J]. Construction and Building Materials, 2013, 44: 626−638.

[10] DU Xiuli, JIN Liu. Meso-scale numerical investigation on cracking of cover concrete induced by corrosion of reinforcing steel[J]. Engineering Failure Analysis, 2014, 39(4): 21−33.

[11] 唐孟雄, 陈晓斌. 基于扩孔理论的混凝土钢筋锈胀开裂分析[J].中南大学学报(自然科学版), 2010, 41(3): 1172−1177. TANG Menxiong, CHEN Xiaobin. Analysis of rebar rust cover cracking in reinforced concrete with cylindrical cavity expansion theory[J]. Journal of Central South University(Science and Technology), 2010, 41(3): 1172−1177.

[12] VU N A, CASTEL A, FRANÇOIS R. Response of post- tensioned concrete beams with unbonded tendons including serviceability and ultimate state[J]. Engineering Structures, 2010, 32(2): 556−569.

[13] CAVELL D G, WALDRON P. A residual strength model for deteriorating post-tensioned concrete bridges[J]. Computers and Structures, 2001, 79(4): 361−373.

[14] WANG Lei, ZHANG Xuhui, ZHANG Jianren, et al. Effect of insufficient grouting and strand corrosion on flexural behavior of PC beams[J]. Construction and Building Materials, 2014, 53(4): 213−224.

[15] 王传志, 滕智明.钢筋混凝土结构理论[M]. 北京: 中国建筑工业出版社, 1985: 64−67. WANG Chuanzhi, TENG Zhiming. Principle of concrete reinforcement structure[M]. Beijing: China Architecture & Building Press, 1985: 64−67.

[16] MOLINA F J, ALONSO C, ANDRADE C. Cover cracking as a function of bar corrosion: part2-Numberical model[J]. Materials and Structures, 1993, 26(9): 535−548.

[17] JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

Calculation of corrosion-induced cracking in prestressed concrete structure

ZHANG Jianren, DAI Lizhao, ZHANG Xuhui, WANG Lei

(School of Civil Engineering & Architecture, Changsha University of Science & Technology, Changsha 410114, China)

An analytical model of three stages of micro-crack, the initiation and the propagation of the corrosive cracks was proposed for the problem of the concrete corrosion cracking induced by prestressing strand corrosion. The concrete under the biaxial stress state, and the geometric properties of strand were incorporated in the model. The sensitivity of influencing factors on corrosion-induced cracking was discussed based on the proposed model. The proposed model was verified with the experimental results. The results show that the prestress of strand has an adverse effect on the corrosion-induced cracking. The corrosion loss in the micro-crack formation, cover cracking, and 0.1 mm wide cracking decreases by 46.14%, 43.90% and 9.42%, respectively, when the prestress changes from stress-free to 75% the standard value of tensile strength. The corrosion loss of the three stages decreases with the increase of rust expansion rate and strand diameter, while it increases with the increase of concrete tensile strength and concrete cover.

bridge engineering; corrosion-induced cracking; prestressing strand; corrosion; biaxial stress state

10.11817/j.issn.1672-7207.2016.09.043

TU375

A

1672−7207(2016)09−3231−08

2015−09−13；

2015−11−03

国家重点基础研究发展规划(973计划)项目(2015CB057705)；国家自然科学基金资助项目(51678069)；湖南省杰出青年基金资助项目(14JJ1022) (Project(2015CB057705) supported by the National Basic Research Development Program (973 Program) of China; Project(51678069) supported by the National Natural Science Foundation of China; Project(14JJ1022) supported by the National Science Foundation for Distinguished Young Scholars of Hunan Province)

王磊，博士，教授，从事既有桥梁可靠性和耐久性研究；E-mail: leiwlei@hotmail.com

(编辑 刘锦伟)