渗流作用下重叠隧道施工引起地层变形

唐晓武，甘鹏路，刘维，赵宇



渗流作用下重叠隧道施工引起地层变形

唐晓武1，甘鹏路1，刘维1，赵宇2

(1. 浙江大学滨海与城市岩土工程研究中心，浙江杭州，310058；2. 浙江大学防灾工程研究所，浙江杭州，310058)

以深圳地铁5号和7号线重叠段为背景，采用三维数值分析方法，对渗流作用下重叠隧道施工引起的地层变形规律进行研究，并与实测数据校验，分析开挖应力释放和地下水渗流共同作用对地层变形的影响。研究结果表明：纵向截面内，7号线施工时上覆地层变形较小，变形范围最远发展至开挖面前方4倍隧道高度处，5号线施工则造成较大地层变形，渗流引起开挖面前方2倍隧道高度范围内水位下降，拱顶上方局部土层出现整体下沉；横向截面内，7号线施工引起的土体变形仍然较小，变形区域可由1条与洞周相切、倾斜角度为的斜线确定，在渗流影响下，5号线施工时截面内水位逐渐降低，土体变形加剧，同时变形范围扩大，地表沉降槽宽度大幅增加；整个施工过程中，地表经历约40 d的快速沉降，速率维持在1 mm/d以上，通过设置止水措施能够有效减小最终沉降，然而当重叠隧道开挖面间距大于一定数值时(本工程为12 m)，间距增大对计算沉降量影响较小，通过减小开挖面间距可以缩短工期。

重叠隧道；地层损失；地下水渗流；地层变形；地表沉降

近年来，为了缓解日益严重的交通拥堵问题，国内外大中型城市正在大规模修建地铁线路。随着地铁线路逐步增加，隧道之间重叠的现象随之出现，使隧道施工面临新的挑战。MAIR等[1]通过分析总结重叠隧道施工中的一些常见问题，认为施工引起的土体变形值得特别关注，修建重叠隧道时，地表与地下结构物的主要风险来源于地层变形，了解地层变形规律能够准确评价并降低这些风险。从施工角度一般可以将重叠隧道分为2类：1) 在既有隧道附近施工1条新的隧道；2) 2条隧道在开挖面保持一定距离的前提下同时施工。其中第1类工程较为常见，国内外学者通过现场监测、模型试验、数值模拟等方式，对新建隧道施工对既有隧道影响的问题进行了大量研究，相关成果已经十分成熟[2−12]。第2类工程则出现较少，尤其是上下重叠的情况。在同时施工过程中，由于开挖面间距较短，不但隧道间存在强烈的相互作用，而且周围地层可能在多次扰动后出现过大变形，因此第2类工程比第1类工程施工风险更大。然而前人对于上下重叠隧道同时施工问题的研究较为欠缺，为了深入探讨此类工程施工引起地层变形规律，本文作者选取深圳地铁5号线5307标重叠段工程进行案例分析。施工过程中，地下水渗流使地层变形问题更加突出。针对该工程，采用FLAC3D有限差分软件开展三维数值分析，通过与现场实测数据校对，分别从模型纵截面地层变形、横截面地层变形和地表沉降发展3个方面，研究了开挖地层损失和地下水渗流对地层变形的共同影响。

1 工程概况

深圳地铁5号线5307标隧道重叠段包含5号线施工段与7号线预留段，其中5号线由2号竖井出发，设计为双联拱隧道过渡到双洞并行隧道的形式，7号线由3号竖井出发，设计为双洞并行隧道，5号和7号线均朝太安站方向施工，5号线位于7号线上方，如图1所示，图中，60 m双联拱重叠段为本文研究区域。在研究区域内根据施工监测方案选取1条纵向地表监测线和半条横向地表监测线，其中纵向测点L1~L6均匀布置在双联拱重叠段内，间隔为10 m，横向测点T1~T4及L4的布置方式见图2。

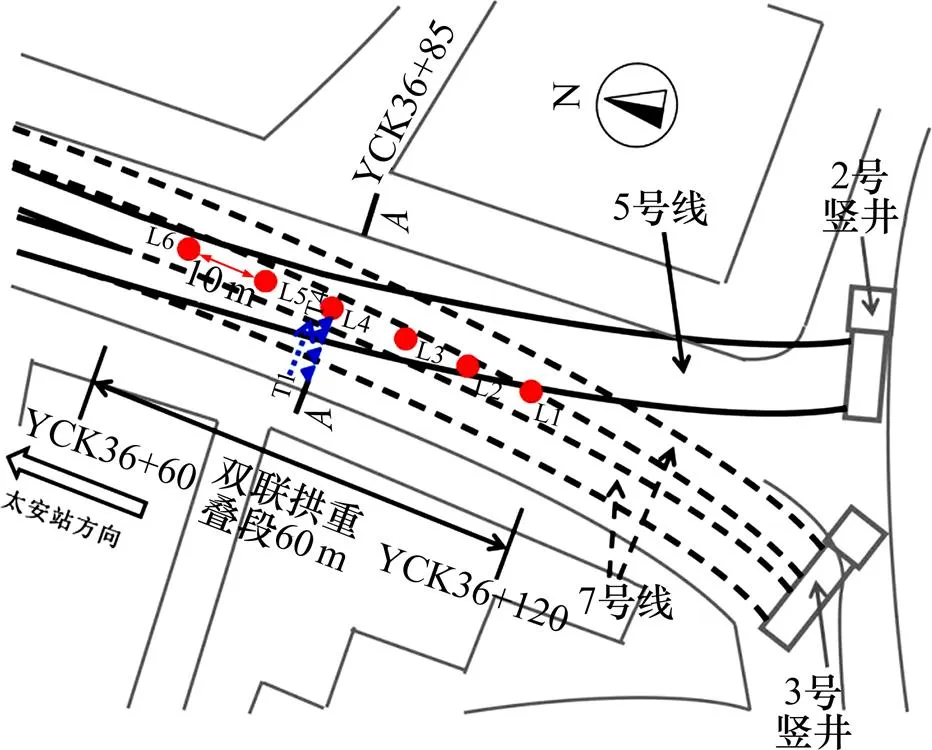
图1 隧道重叠段平面布置图

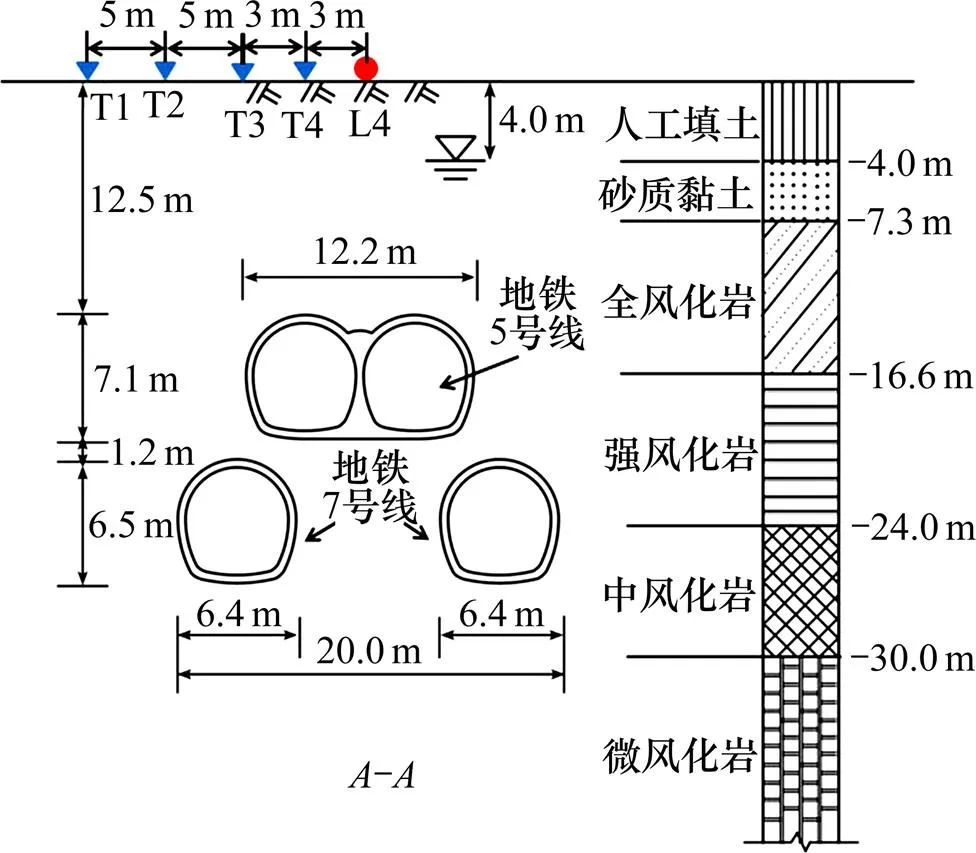
图2 横断面A−A布置图

横向监测线所处横断面−如图2所示，5号和7号线在此断面重合度高。5号线隧道宽12.2 m，高7.1 m，主要穿越地层为震旦系全风化及强风化混合岩；7号线宽6.4 m，高6.5 m，左右线间距7.2 m，主要穿越地层为强风化及中风化混合岩，2条线路上下净距离仅有1.2 m。重叠隧道覆土厚为12.5 m，由人工填土、砂质黏土和全风化混合岩组成。整个研究区域为富水地层，地下水位在地下4.0 m处。

2条地铁线路均采用台阶法施工，台阶长度约为4 m，其中5号线双联拱隧道分为中导洞和左右2个主洞，首先开挖中导洞，中导洞封闭成环后再逐步开挖左右主洞。为满足工期要求，5号和7号线同时施工，7号线在前，2条并行隧道开挖面之间存在3~5 m的间距，5号线在后，与较近的7号线开挖面保持 26 m的距离。5号和7号线的开挖速度平均为1 m/d。在7号线开挖前进行全断面注浆止水，注浆深度约为1 m，使隧道周边形成封闭的止水区域，以保证上方5号线稳定，而5号线未采取全断面止水措施进行预加固，在其施工过程中存在一定程度的地下水渗流。

2 数值模拟

考虑7号线并行隧道开挖面间距较短，模拟时假设2条隧道对称施工，根据图2中隧道布置情况，采用有限差分软件FLAC3D建立半个轴对称三维数值模型如图3所示。模型的长×宽×高为90 m×40 m×40 m，共16 932个单元，18 970个节点。沿开挖方向(轴正方向)对模型中间60 m单元网格进行加密作为本文计算分析区域，对应图1中60 m双联拱重叠段，前15 m重叠隧道单元在计算前开挖，代表已施工完毕的重叠段，形成较为真实的地应力场。地下水面设置在地表下方4.0 m。在2个侧面边界=−40 m和=0 m上限制方向位移，在另外2个侧面边界=0 m和=90 m上限制方向位移，在底部边界=−40 m上限制方向位移。数值计算参数由地质勘测报告确定，见表1。土层采用摩尔−库仑模型(Mohr-Coulomb model)，摩尔−库仑屈服准则由2部分组成，其中剪切破坏准则定义为：

拉伸破坏准则定义为

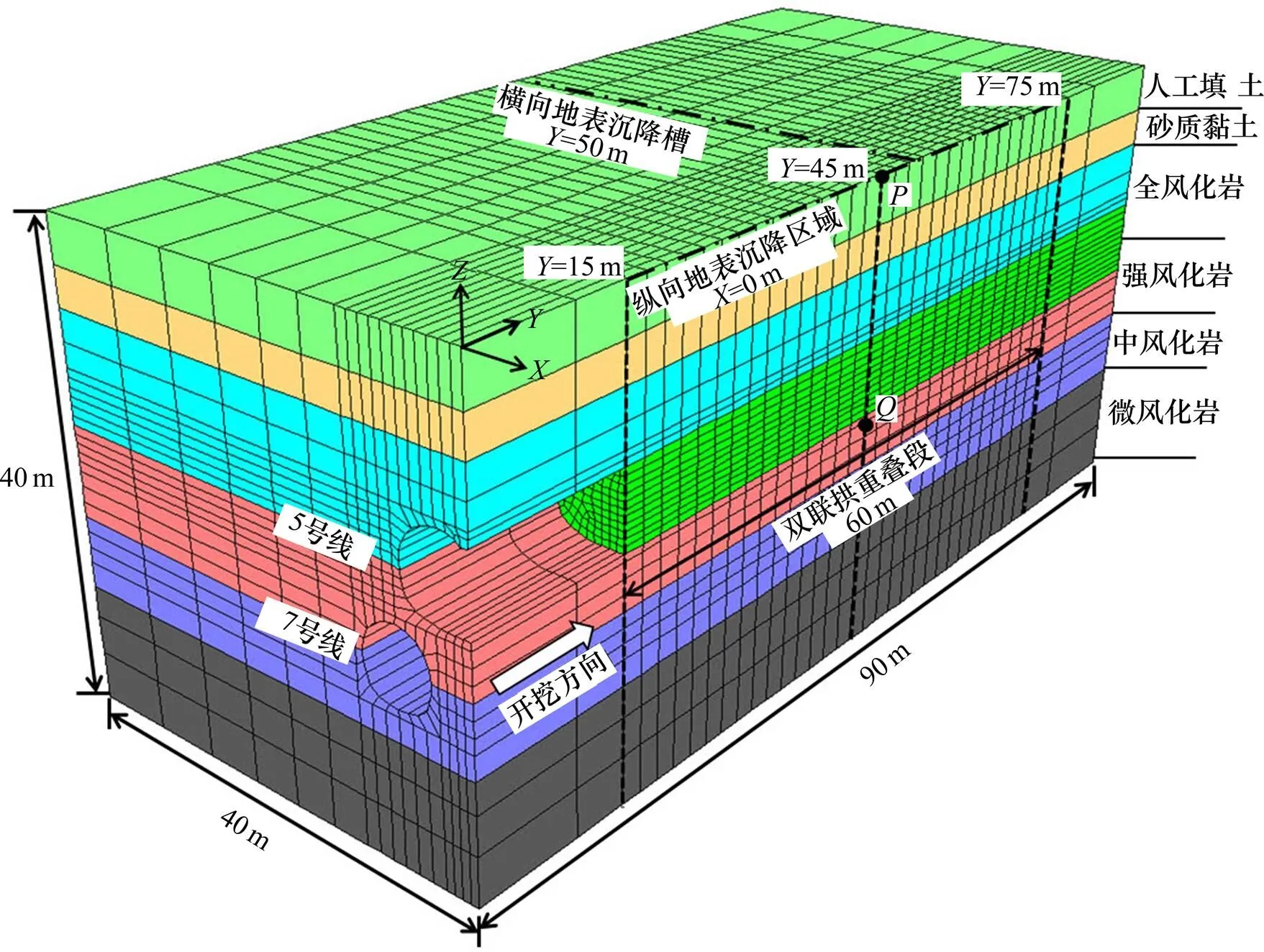
图3 三维数值模型

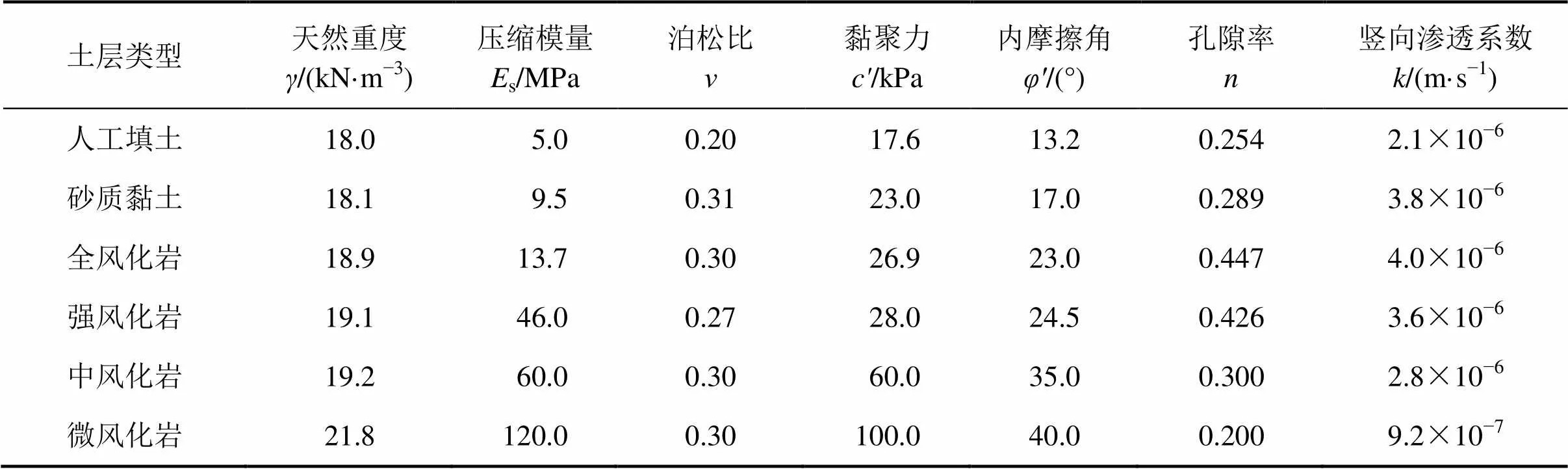
表1 地层力学参数

由于水文地质参数有限，本文假设地层水平渗透系数与竖向渗透系数一致，采用各向同性渗流模型进行渗流计算，符合达西定律(Darcy’s law)：

流固耦合计算符合Biot固结理论，多孔介质的控制方程为

图4所示为数值计算时横断面内的注浆范围，沿开挖方向注浆超前开挖面2 m。采用提高土体模量的方法模拟注浆加固效果，本文参照刘润等[13]的研究结果，将风化岩体注浆区域的压缩模量提高80%。

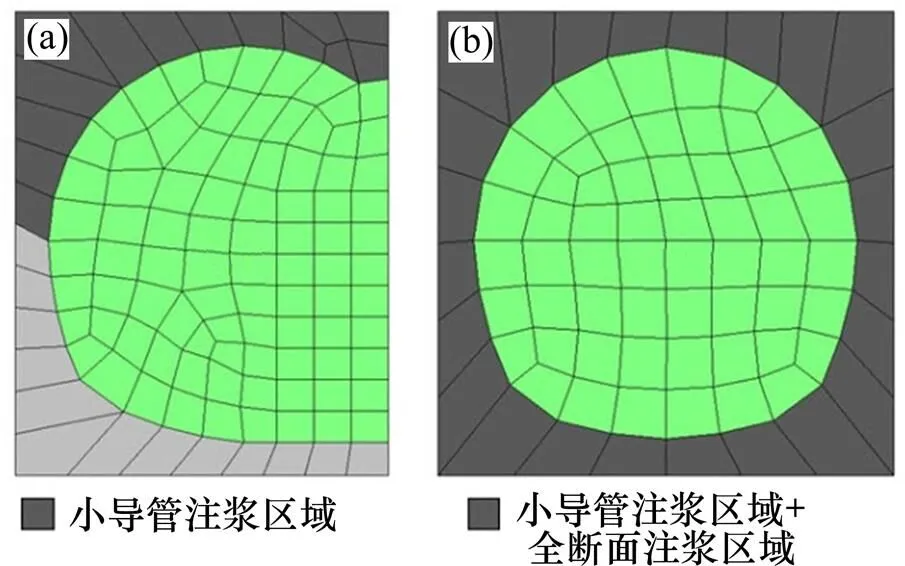
(a) 5号线；(b) 7号线

对5号和7号线进行分部开挖，上下台阶每次开挖一环网格(2 m)。采用PANET等[14]提出的应力释放法模拟开挖后围岩自稳过程，在模型开挖边界施加反向应力以控制实际的不平衡力，节点应力释放率由监测数据反演确定，为20%。接着施加shell结构单元模拟初期支护，初支混凝土强度等级为C25，其力学参数为：弹性模量=28.0 GPa、厚度=0.3 m、泊松比=0.3。由于7号线在开挖前采取了全断面注浆止水措施，故假设其开挖边界为不透水界面，边界处流量设置为0，而5号线内存在地下水渗流，参照YOO等[15]的工程案例研究，将开挖边界上的孔压设置为0 Pa，模拟地下水渗流。根据平均施工速度，每开挖一环单元网格的渗流时间设置为2 d。考虑到开挖时间远小于渗流时间，在计算隧道开挖引起的地层变形时假定土体孔压保持不变，仅开启力学计算模式，然后再开启流体模式，采用流固耦合计算地层的渗流固结变形[16]。

图5所示为重叠隧道同时开挖的模拟过程，前 26 d仅开挖7号线，第26天至第60天5号和7号线同时开挖，开挖面之间保持26 m的距离，第60天至第86天开挖5号线。

1—第26天；2—第42天；3—第60天；4—第86天。

3 纵截面地层变形分析

图6所示为纵向地表沉降区域(图3中截面=0 m)的发展历程，4条纵向沉降曲线依次对应4个时间点的监测数据(重叠段施工前的沉降未记录在内，监测频率为1次/d)。由于计算模型与监测点L1和L2下方隧道布置情况不同，模拟结果与实测值相差较大，其他部分则较为吻合。前26 d，在7号线开挖应力释放的作用下，纵向沉降曲线发展缓慢，最大深度为26.7 mm，仅达到最终深度的30%。第26天至第42天，5号线开挖引起地下水渗流，上覆地层的孔隙水压力逐渐降低(图7)，进而引起地层固结变形，与应力释放引起的变形叠加后，上方地表出现大幅沉降，最大增长为44.2 mm，而7号线上方地表沉降增长仍然缓慢，最大增长为29.2 mm，与前26 d类似。第42天至第86天，最大沉降位置随着5号线开挖面一起移动，最大沉降持续增长至95.2 mm，其中5号线开挖引起的沉降约占70%，故5号线施工是纵向地表沉降剧烈发展的主要阶段。

图6 纵向地表沉降发展过程

单位：m

图8所示为截面=0 m内地层竖向变形等值线图。由图8(a)可见：第26天时，7号线开挖应力释放引起的最大竖向变形为38 mm，出现在7号线拱顶侧上方地层中，变形主要朝地表发展，对7号线侧下方地层影响较弱，至7号线底面处变形减小至0。应力释放对开挖面前方地层影响也较为有限，开挖面前方47远处(7为7号线高度)土层竖向变形已接近于0。由图8(b)可见：第42天时，在5号线应力释放与地下水渗流共同作用下，地层最大竖向变形增长了52 mm，是7号线开挖变形的1.4倍。虽然应力释放引起的土体变形朝地表方向逐渐减小，但固结变形累积增大，两者叠加造成5号线拱顶上方出现7 m高的地层整体沉降。由于5号线开挖面前方25(5为5号线高度)以内地下水头存在明显改变(图7)，地层固结变形主要发生在该范围内。

单位：mm (a) 第26天；(b) 第42天

4 横截面地层变形分析

图9所示为横向地表沉降槽(图3中截面=50 m)的发展历程。由于重叠段内5号和7号线相对位置多变，施工过程中模拟结果与实测值存在一定差异，但最终两者较为吻合。第26天时，7号线开挖面与研究截面的距离为9 m，沉降槽最大深度仅有8.1 mm，故在隧道穿越研究截面前，应力释放对横向地表沉降的影响微小。第42天时，7号线开挖穿过研究截面，5号线开挖面与研究截面的距离为19 m(＞25)，截面内水位基本未改变(图10(a))，故沉降槽的发展主要源于7号线开挖应力释放，最大深度增长25.9 mm，宽度基本不变。第60天时，5号线开挖面与研究截面的距离为1 m，截面内水头显著降低(图10(b))，地层产生固结沉降。与前42 d不同，沉降槽宽度剧烈发展，边界=−40 m处地表出现了6.2 mm的大幅沉降，可见渗流对横向地表沉降的影响范围要远大于开挖应力释放的影响范围。第86天时，5号线开挖穿过研究截面，水头进一步下降(图10(c))，=−40 m处地表沉降增长11.6 mm，沉降槽宽度再次扩大。因此，在渗流环境下进行隧道施工，需要在更大的范围内保护土层中的基础及地下管线。

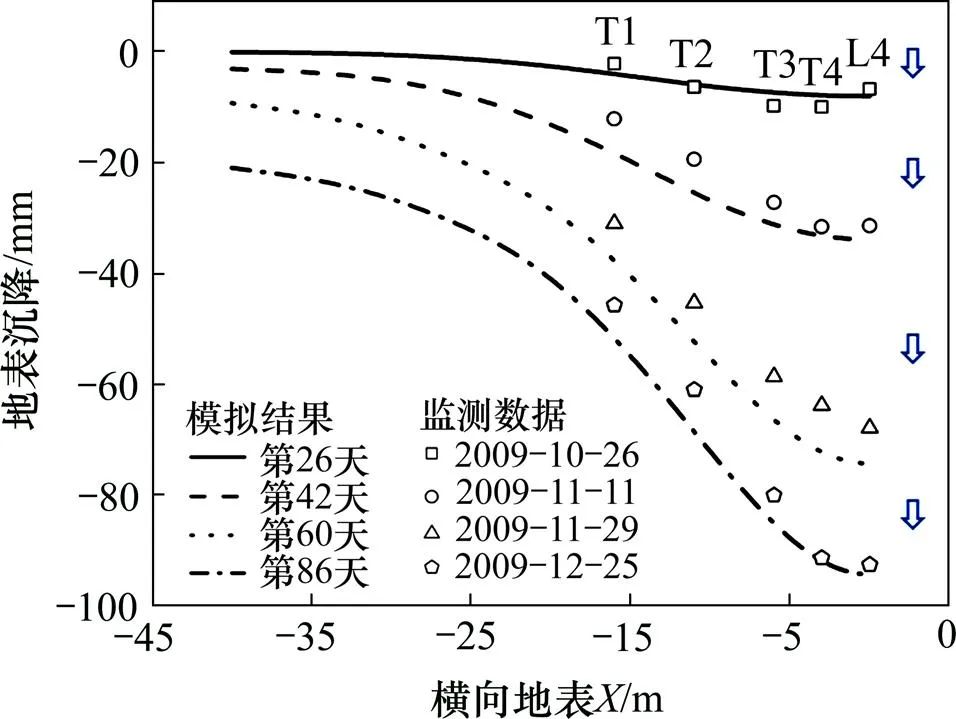
图9 横向地表沉降槽发展过程

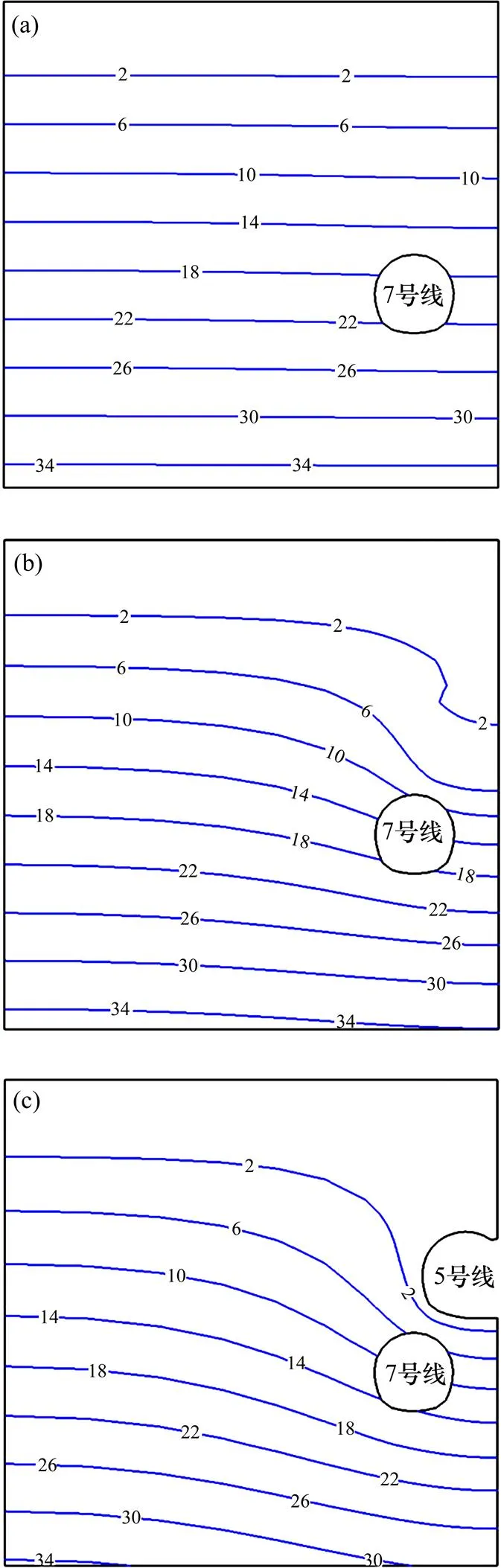
(a) 第42天；(b) 第60天；(c) 第86天

图11所示为5号线不透水与透水条件下的最终横向地表沉降槽。在不透水条件下，模型边界处的地表沉降接近于0 mm，在透水条件下，渗流作用致使横向地表沉降槽下移，验证了地下水渗流是扩大沉降槽宽度的重要原因。

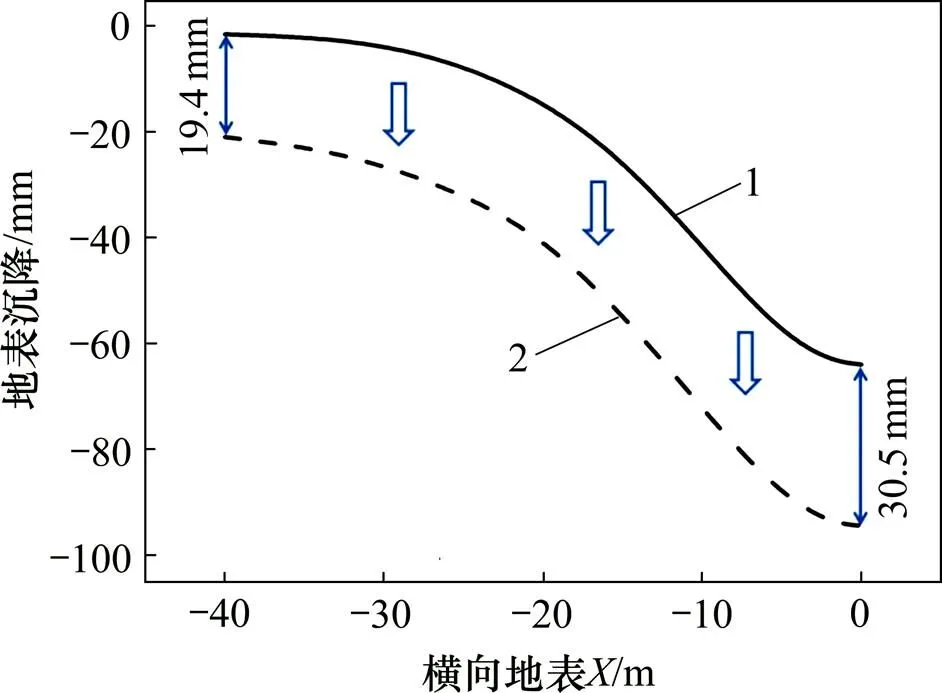
1—5号线不透水；2—5号线完全透水。

图12所示为截面=50 m内地层竖向变形等值线图，图中数值为竖向变形。如上所述，前42天内7号线开挖应力释放是地层变形的主要原因。第42天时，7号线拱顶处竖向变形最大，沿洞圈向下迅速减小，至边墙处仅剩10 mm(图12(a))。上覆地层变形区域大致可以由1条与洞圈相切的斜线确定，水平方向的夹角为，其中为上覆地层内摩擦角平均值(25°)，这与ATTEWELL[17]的研究成果一致。第86天时，5号线开挖穿过研究截面，由于5号和7号线均采用台阶法施工，大致认为5号线应力释放引起的土体变形区域仍可用1条倾斜角度为的斜线确定。斜线内侧土体变形由应力释放变形和渗流引起的固结变形叠加而成，斜线外侧土体变形主要是固结变形，整个上覆地层竖向变形的大小及范围显著增大(图12(b))。然而上覆土层有效应力增加未使7号线拱顶至5号线中轴线区域土层变形出现太大变化。

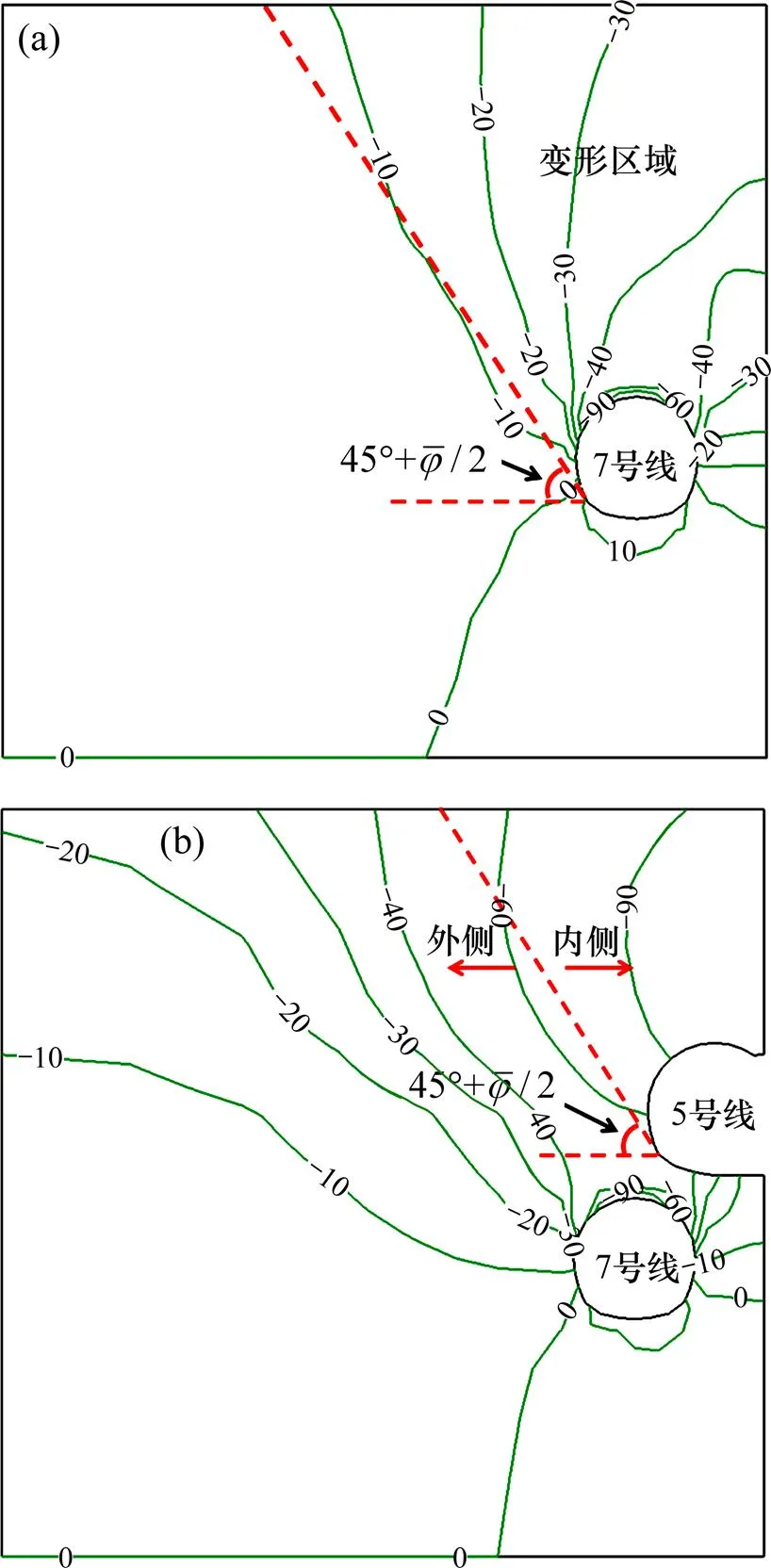
单位：mm (a) 第42天；(b) 第86天

5 地表沉降发展过程

为全面反映施工过程中地表沉降发展过程，选择模型中间截面=45 m内的地表点(图3)进行研究，点沉降随时间发展曲线如图13所示。由于监测点L4与点十分接近，且处在用于建模的横断面−内，故采用该监测点数据进行对比，发现两者发展趋势较为一致。由图13可见：地表沉降发展存在2个拐点：第24天和第63天，此40 d内沉降快速增长，共计产生80 mm的沉降，占最终沉降的85%。因此，同时施工过程中存在一个持续时间长、沉降大的快速增长阶段，该阶段对应的施工过程为：7号线开挖面落后点1倍7距离至5号线开挖面超过点1倍5距离。对于既有地表建筑物，在上述施工阶段应加强监测。

1—模拟曲线；2—监测数据(2009−10−01—2010−01−03)。

为研究沉降速率与压力水头之间的关系，绘制了点沉降速率和点(图3)压力水头随时间变化曲线如图14所示，其中点位于点正下方、5号线底部。前30 d，点沉降速率持续上升，在7号线开挖面到达其正下方时达到第1个峰值：1.75 mm/d。此时间段内，点压力水头维持在16 m不变，渗流影响可以忽略，由于开挖应力释放的影响持续加剧，沉降速率不断上升。随后10 d，5号线开挖引起点压力水头下降，渗流影响开始出现并缓慢增加，而7号线应力释放的影响逐渐减弱，两者共同作用后点沉降速率基本维持稳定。接下来13 d，点沉降速率在第1个峰值基础上继续增加，在5号线开挖面与点距离缩短为3 m时达到第2个峰值：2.83 mm/d，该值比第1个峰值提高了60%。此时间段内，5号线开挖应力释放的影响逐渐增强，同时点压力水头急剧下降(峰值处水头下降速率最大)，渗流影响显著增大，共同导致沉降速率继续上升。最后33 d，点沉降速率从峰值逐渐减小至0，5号线应力释放和渗流的叠加影响开始减弱。在快速增长阶段内，点沉降速率基本维持在1 mm/d以上。

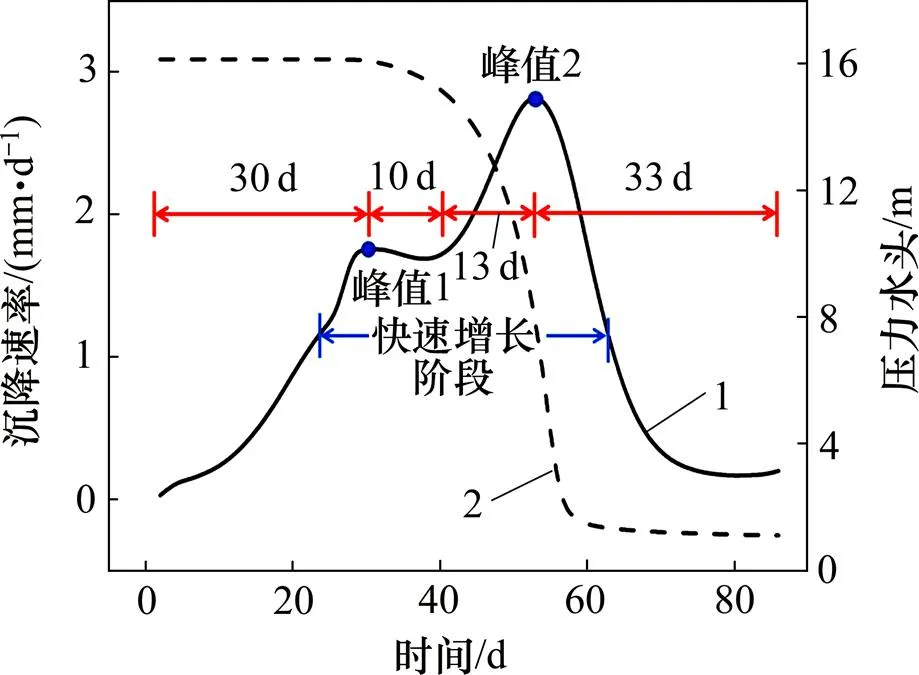
1—P点沉降速率；2—Q点压力水头。

图15所示为不同透水条件对地表沉降发展过程的影响。除实际工况(曲线(b))外，考虑2个极端情况：一是5号和7号线的开挖边界均不透水，二是5号和7号线的开挖边界均完全透水，开挖边界均不透水时，最终沉降为65 mm，由于5号线透水引起固结变形，本文工况下的最终沉降增长至95 mm，较开挖边界均不透水时上升了45%，开挖边界均完全透水时，最终沉降增长至101 mm，较开挖边界均不透水时上升了55%，故渗流引起的固结沉降在总沉降中占据了相当大的比例，实际施工过程中可以通过设置止水措施来减小最终沉降。由于隧道断面的止水效果可能存在差异，上、下隧道内部会发生不同程度的渗流，然而地下水渗流量及其引起的地下水头重分布总是介于上述2种极端情况之间。

1—5号和7号线均不透水；2—本文工况；3—5号和7号线均透水。

图16所示为不同开挖面间距对地表沉降发展过程的影响。当5号和7号线开挖面间保持0 m和12 m施工时，地表最终沉降分别为79 mm和94 mm，当开挖面间保持26，38和60 m施工时，地表最终沉降均为95 mm，可见：当上、下重叠隧道开挖面间距超过一定长度后(本工程为12 m)，开挖面间距对地表最终沉降几乎没有影响。随着开挖面间距加长，7号线开挖面经过点到5号线开挖面经过点的时间延长了，两者共同影响区域相应缩短，此时间段内的沉降发展逐渐平缓。在考虑隧道间相互作用的前提下，可以适当缩小同时施工时的开挖面间距，以缩短施工时间。

开挖面间距/m：1—0；2—12；3—本文工况；4—38；5—60。

6 结论

1) 开挖5号和7号线会在地层中造成一定程度的应力释放，同时5号线开挖引起地下水渗流，改变地下水位分布，三者共同作用后形成了复杂的三维地层变形。

2) 纵向截面内，7号线施工时上覆地层变形较小，变形范围最远发展至开挖面前方4倍隧道高度处，地表沉降发展30%。5号线施工时上覆地层变形较大，开挖面前方2倍隧道高度范围内水位显著降低，拱顶上方部分土层整体下沉，剩余70%地表沉降发展完全。

3) 横向截面内，7号线施工引起的地层变形仍然较小，变形区域可由1条与洞周相切且与水平方向夹角为的斜线确定，地表沉降槽宽度基本保持不变。5号线施工大幅加剧了地层变形，在渗流作用下，地层沉降范围显著扩大，地表沉降槽宽度增加。

4) 从7号线开挖面落后1倍隧道高度到5号线开挖面超过1倍隧道高度过程中，地表经历长时间快速沉降，速率维持在1 mm/d以上。设置止水措施能够有效减小地表最终沉降，而在一定范围内减小开挖面间距对最终沉降几乎没有影响。

[1] MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays[J]. Géotechnique, 1993, 43(2): 315−320.

[2] CHEN S L, GUI M W, YANG M C. Applicability of the principle of superposition in estimating ground surface settlement of twin- and quadruple-tube tunnels[J]. Tunnelling and Underground Space Technology, 2011, 28(1): 135−149.

[3] HAGE CHEHADE F, SHAHROUR I. Numerical analysis of the interaction between twin-tunnels: influence of the relative position and construction procedure[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 210−214.

[4] HEFNY A M, CHUA H C, ZHAO J. Parametric studies on the interaction between existing and new bored tunnels[J]. Tunnelling and Underground Space Technology, 2004, 19(4/5): 471.

[5] YAMAGUCHI I Y, KIRITANI Y. Study on ground-tunnel interactions of four shield tunnels driven in close proximity[J]. Tunnelling and Underground Space Technology, 1998, 13(3): 289−304.

[6] YANG G R, YANG P F, FAN C B. Ground settlement troughs induced by multiple shield tunneling[C]// Proceedings of 2nd International Symposium on Structures and Foundations in Civil Engineering. Hong Kong, China, 1997: 744−745.

[7] 陈先国, 高波. 重叠隧道的施工力学研究[J]. 岩石力学与工程学报, 2003, 22(4): 606−610. CHEN Xianguo, GAO Bo. Research on construction mechanics of overlapping tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(4): 606−610.

[8] 黄俊, 张顶立. 地铁重叠隧道上覆地层变形的数值模拟[J]. 岩石力学与工程学报, 2005, 24(12): 2176−2182. HUANG Jun, ZHANG Dingli. Numerical simulation of stratum deformation above overlapping metro tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2176−2182.

[9] 孙钧, 刘洪洲. 交叠隧道盾构法施工土体变形的三维数值模拟[J]. 同济大学学报, 2002, 30(4): 643−646. SUN Jun, LIU Hongzhou. 3-D numerical simulation of ground surface settlement under overlapped shield tunneling[J]. Journal of Tongji University, 2002, 30(4): 643−646.

[10] 杨小礼, 眭志荣. 浅埋小净距偏压隧道施工工序的数值分析[J]. 中南大学学报(自然科学版), 2007, 38(4): 764−770. YANG Xiaoli, SUI Zhirong. Numerical simulation of construction sequence for shallow embedded bias tunnels with small clear distance[J]. Journal of Central South University (Science and Technology), 2007, 38(4): 764−770.

[11] 张海波, 殷宗泽, 朱俊高. 近距离叠交隧道盾构施工对老隧道影响的数值模拟[J]. 岩土力学, 2005, 26(2): 282−286. ZHANG Haibo, YIN Zongze, ZHU Jungao. Numerical simulation of influence of new tunnel on short distance overlapped old tunnel during shield tunneling[J]. Rock and Soil Mechanics, 2005, 26(2): 282−286.

[12] 章慧健, 仇文革, 冯冀蒙, 等. 近距离重叠隧道盾构施工的纵向效应及对策研究[J]. 岩土力学, 2010, 31(11): 3569−3573. ZHANG Huijian, QIU Wenge, FENG Jimeng, et al. Study of longitudinal mechanical behavior and countermeasure for neighborhood overlapped shield tunneling[J]. Rock and Soil Mechanics, 2010, 31(11): 3569−3573.

[13] 刘润, 闫玥, 闫澍旺, 等.强风化岩质边坡滑坡治理及有限元分析[J]. 岩石力学与工程学报, 2006, 25(s1): 2790−2794. LIU Run, YAN Yue, YAN Shuwang, et al. Improvement and finite element analysis of an intense weathering rock slope[J]. Chinese Journal of Rock Mechanics and Engineering,2006, 25(s1): 2790−2794.

[14] PANET M, GUENOT A. Analysis of convergence behind the face of a tunnel[C]// Proceedings of the 3rd International Symposium of Institution of Mining and Metallurgy. Brighton, UK, 1982: 194−204.

[15] YOO C, LEE Y, KIM S H, et al. Tunnelling-induced ground settlements in a groundwater drawdown environment: a case study[J]. Tunnelling and Underground Space Technology, 2012, 29(1): 69−77.

[16] Itasca Consulting Group Inc. Fast lagrangian analysis of continua in 3 dimensions (Version 3.0)[M]. Minneapolis: Itasca Consulting Group Inc., 2003: 36−57.

[17] ATTEWELL P B. Ground movements caused by tunneling in soil[C]// Proceedings of International Conference on Large Movements and Structures. London, UK: Pentech Press, 1978: 812−948.

Ground deformation induced by overlapped tunneling under seepage condition

TANG Xiaowu1, GAN Penglu1, LIU Wei1, ZHAO Yu2

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China; 2. Institute of Disaster Prevention Engineering, Zhejiang University, Hangzhou 310058, China)

Based on the engineering background of the overlapped section of Line No.5 and Line No.7 of Shenzhen Metro, three-dimensional numerical analysis was used to investigate the ground deformation induced by overlapped tunneling under seepage condition, and the computed deformations were verified by monitoring data. The combined effects of stress relief induced by excavation and groundwater seepage on ground deformation were analyzed. The results show that in the longitudinal section, the deformation of overlying strata during the tunneling of Line No.7 is small. The deformation range ahead of the excavation face of Line No.7 does not exceed 4 times of tunnel height. However, the deformation of overlying strata during the tunneling of Line No.5 is much larger. The groundwater level drops within the range of 2 times of tunnel height ahead of excavation face of Line No.5 due to seepage. Overall settlement arises in the local soil above the vault. In the transverse section, the deformation induced by the tunneling of Line No.7 is still small, and the deformation area can be determined by a tangent line of the tunnel that has an inclined angle ofwith the horizontal direction. Affected by seepage, the groundwater level in the section gradually decreases during the tunneling of Line No.5, which not only increases the ground deformation, but also enlarges the settlement range, and the width of surface settlement trough increases noticeably. During the whole construction, the surface settlement experiences rapid increments for about 40 d. The settlement rate maintains more than 1 mm/d. Setting up sealing measures can effectively reduce the final surface settlement. However, when the distance between excavation faces of overlapped tunnels is more than a certain value (12 m for this project), enlarging the distance has a little influenceon the final settlement. Thus, the construction time can be shortened through reducing the distance between excavation faces.

overlapped tunnels; ground loss; groundwater seepage; ground deformation; surface settlement

10.11817/j.issn.1672-7207.2016.09.027

TU47

A

1672−7207(2016)09−3108−09

2015−06−15；

2015−10−11

国家自然科学基金资助项目(51338009，51208461)；华东勘测设计研究院科技项目(KY2013-02-30) (Projects(51338009, 51208461) supported by the National Natural Science Foundation of China; Project(KY2013-02-30) supported by Fund of Power China Huadong Engineering Corporation Limited)

赵宇，博士，助理研究员，从事工程地质研究；E-mail: zhao_yu@zju.edu.cn

(编辑 赵俊)