基于Meta分析的青海杂多地区成矿定量预测

潘勇，彭省临，彭光雄, 2



基于Meta分析的青海杂多地区成矿定量预测

潘勇1, 3，彭省临1，彭光雄1, 2

(1. 中南大学地球科学与信息物理学院，长沙 410083；2. 大陆构造与动力学国家重点实验室，北京100037；3. 厦门大学嘉庚学院，厦门，363105)

为降低权重确定的不确定性，将循证医学领域广泛使用的Meta 分析方法用于定量预测青海杂多地区的矿产资源。在分析该地区成矿规律与控矿因素的基础上，选择地层、构造、岩浆岩、地磁异常、化探异常和遥感蚀变异常这6个要素的11个预测因子，构建成矿定量预测的指标体系。以区内的50多个已知矿点为样本，采用规则网格单元统计上述11个预测因子与已知矿点的空间位置套合情况，从而将地质资料中的非定量数据转化为Meta分析所要求的定量信息，并通过Meta分析计算得到不同预测因子的优势比。通过分析各个预测因子之间优势比之差，结合模糊综合层次分析法(FAHP)求得各个因子在成矿预测中的权重。基于该权重，利用模糊综合评判(FCA)建立青海杂多地区铅锌多金属矿的成矿定量预测模型，并划分出3类不同级别的成矿有利区。以此为基础，划定出5个成矿远景区，圈定A类勘查靶区5处，B类勘查靶区10处，C类勘查靶区20处。研究结果表明：基于Meta分析的定量预测法比常规的综合化探异常法的找矿有效性提高36%。

Meta分析；隐伏矿体；模糊综合评判；定量预测

随着数据采集技术、数据处理技术及成矿理论的发展，成矿预测所能借助的方法和技术手段也日益增多，基于多元信息的定量成矿预测成为找矿预测领域的研究热点。由于成矿预测中地质变量的复杂性和不确定性，定量预测地下深部地质体及隐伏矿床非常具有挑战性[1−2]。而定量确定找矿目标与找矿信息之间的关系，是解决上述问题的重要途径与前沿技术之 一[3−5]。权重是定量体现找矿目标与找矿信息的重要指标，因此，科学、客观地确定成矿定量预测中各个信息变量的权重具有十分重要的意义[6−7]。证据权法(weights of evidence)是AGTERBERG[8]提出的一种基于概率不确定性与贝叶斯律的地学统计方法，在成矿定量预测中应用较为广泛。但证据权法要求各个证据层必须是二值化或者是多分类数据，并且参与预测的各个变量之间是必须相互独立的[9]，因而具有一定的局限性。Meta分析(meta-analysis)以其超常规的综合分析能力，广泛应用于心理、教育和医学等领域，是循证医学研究的重要方法，20世纪90年代后开始被引入到生态领域并得到了生态学界的高度重视[10−12]。近几年，研究者开始尝试将Meta 分析应用于找矿预测领域，并在定量处理不确定性的地质数据方面显示出优越性[5, 13−14]。Meta分析的统计量—效应尺度(如相关系数、优势比、对照组与实验组的标准化差值)可给出处理效应的定量结果，解决研究结果的不一致性，并为权重的客观确定提供有效的工具[14−15]。由于Meta分析有利于降低权重确定的不确定性，从而能有效提高多元信息成矿定量预测的能力。为此，本文作者将Meta分析应于定量分析青海杂多铅锌多金属矿区的成矿预测，以期提高该地区的矿产勘查靶区优选的准确性，为进一步找矿部署提供科学依据。

1 Meta分析的原理和方法

Meta分析是一种超常规的综合分析方法[16−17]。刘关键等[16]将Meta分析的统计学过程概括为3部分：合并统计量的选择；异质性检验；合并统计量的假设检验。Meta分析的基础是必须获取大量实验结果的定量数据。Meta分析的初衷是对相同研究主题的相关文献进行综合定量分析[18]，因此，应用于成矿定量预测中时，需要将地质调查与勘探中获取的成矿预测信息进行量化提取，并转化为Meta分析能够识别利用的数据[19−20]。网格单元法是实现上述数据量化提取的有效方法之一。彭省临等[5, 20]通过“微分单元法”实现了成矿定量预测中面向Meta分析的地质数据量化提取。对地质数据量化提取的结果进行Meta分析，可得到不同地质变量的优势比O，从而获得不同地质变量对成矿预测的重要性定量指标。

2 成矿预测指标体系

2.1 地质背景

研究区位于青藏北特提斯成矿域、唐古拉成矿省、沱沱河—杂多华力西期—喜山期铜钼铅锌银成矿带的中西段，也是“三江”成矿带的北延部分。区内地层主要为早石炭世杂多群灰岩及晚三叠世结扎群灰岩。地层之间以断块形式呈北西—南东向展布，与区域构造线基本一致。断裂构造主要为北西—南东走向，其次为北东—南西走向。区内地层、火山岩、侵入岩及矿产的空间展布均受断裂构造控制。已发现的矿化带大部分沿北西—南东向断裂带分布，形成的矿体大部分赋存于其次级断裂带中。火山岩、侵入岩较发育，侵入岩与区内多金属成矿的关系较密切，已发现的矿化多产于岩体外接触带部位的灰岩和矽卡岩中。区内矿产较丰富，尤以铜、钼、铅、锌为主，其次为铁、银等。具有一定规模的矿床有然者涌铅锌银矿床、东莫扎抓铅锌矿床和莫海拉亨铅锌矿床等[4]。

2.2 地质变量的选取

以区内铅锌矿床的成矿规律和控矿因素为依据，选择地层、断裂、岩浆岩、地磁异常、化探异常和遥感蚀变异常这6个要素的11个变量建立成矿预测指标体系(见表 1)。这6个要素的11个地质信息变量通过遥感解译、化探及地磁数据处理、矿化蚀变遥感信息提取等手段进行量化处理。

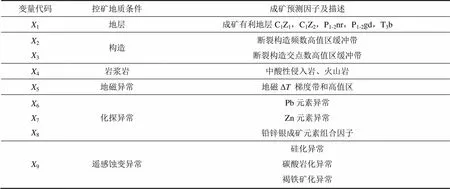
表1 成矿定量预测的指标体系及评分表

2.3 数据量化提取

根据Meta分析的思路和步骤，基于网格单元，可采取多区域法和多级网格法2种方法实现地质资料数据的量化提取。潘勇等的研究表明[14]：采用Meta分析进行数据量化提取时，应优先采用多区域法，其次才能选用多级网格法。由于研究区内的样本数据比较丰富，能够满足多区域法Meta分析量化提取的要求，因此，优先选择多区域法将地质调查中的非定量数据转化为Meta分析所要求的定量信息。

研究区包括12个1:5万比例尺的标准图幅范围，约5 000 km2，其中北部4个图幅的矿床(点)资料较丰富，可以用于进行Meta分析确定指标的权重，然后，利用这4个图幅确定的权重来构建全区12个图幅的成矿定量预测模型。利用多区域法时，将北部4个图幅划分为10个不同的区块进行统计。

网格单元的尺度大小也是影响Meta分析效果的重要因素之一，一般根据区内资料的丰富程度及地区经验来选择[14]。根据区内已有地质调查数据，通过多次试验后发现1 km×1 km是最优网格单元尺度。以1 km×1 km规则网格单元划分研究区信息统计单元，统计上述11个地质信息变量与每个网格的空间位置套合情况。当网格中每包含11个地质信息变量中的1个变量信息时，赋给单元格的值则加1，根据实际情况进行累加。在一般情况下，单元格的赋值越高，则成矿的可能性越大，可暂且将单元格的赋值成矿≥6的单元格设为远景成矿单元格，作为Meta分析的1个参照对象。

分别用全变量组合和缺某个变量的变量组合进行比较，统计已知矿点落在单元格的数量，进行Meta分析，可计算获得相应的优势比O，从而确定地质信息变量对于成矿的相对重要程度。设全变量远景成矿单元格数量为，有矿点落入的实际有矿单元格数量为, 有矿点落入的远景成矿单元格数量为，则基于10个区块的地质资料，利用多区域法可分别统计得到，和，如表2所示。

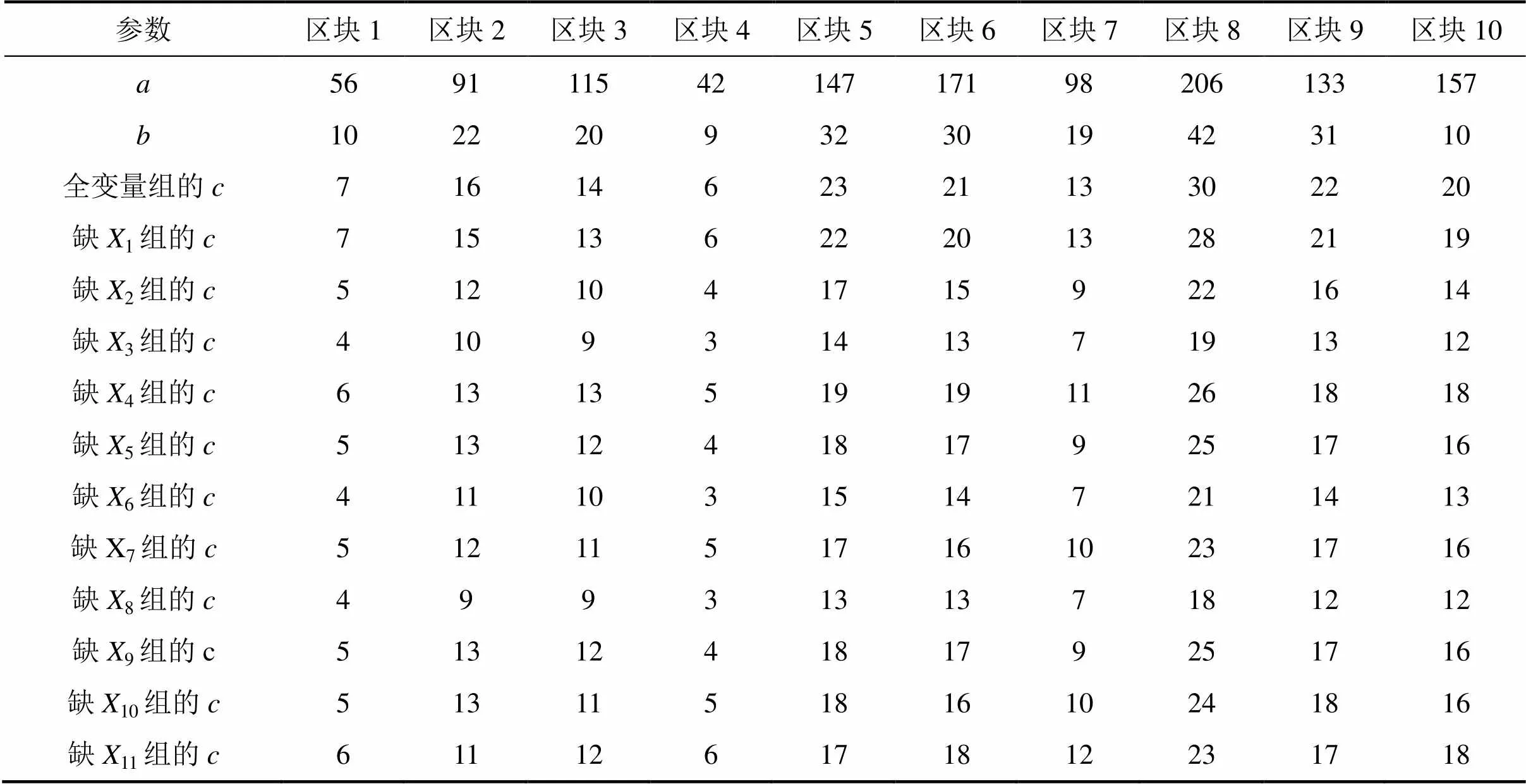
表2 单元格网中的矿点数量统计表

3 Meta分析

Review Managers是用于循证医学Meta分析的软件，由国际Cochrane协作网开发并免费发布。利用Review Manager(V5.1)对表2所示统计结果进行Meta分析。异质性检验结果=1.0，大于0.05，因此，可认为上述的多个独立研究具有同质性，可采用固定效应模型(fixed effect model)计算其合并统计量。缺1变量组森林图中菱形与垂线相交并位于垂直线偏右侧位置，假设检验=0.43，大于0.05，因此，统计学意义不明显。其余2至11共10个变量的假设检验均小于0.05，森林图中菱形完全位于垂直线右侧，结果具有统计学意义。全变量组与缺某个变量组Meta分析所得优势比O如表3所示。优势比O越大，说明对应的变量对成矿的贡献越大，在成矿定量预测中对应变量的权重也就越大。由表3可知：8(铅锌银成矿元素组合因子)对成矿的贡献最大，其O为3.44；其次为3(断裂构造交点数高值区缓冲带)，其O为3.22；1(地层)对成矿的贡献最小，其O仅为1.17。

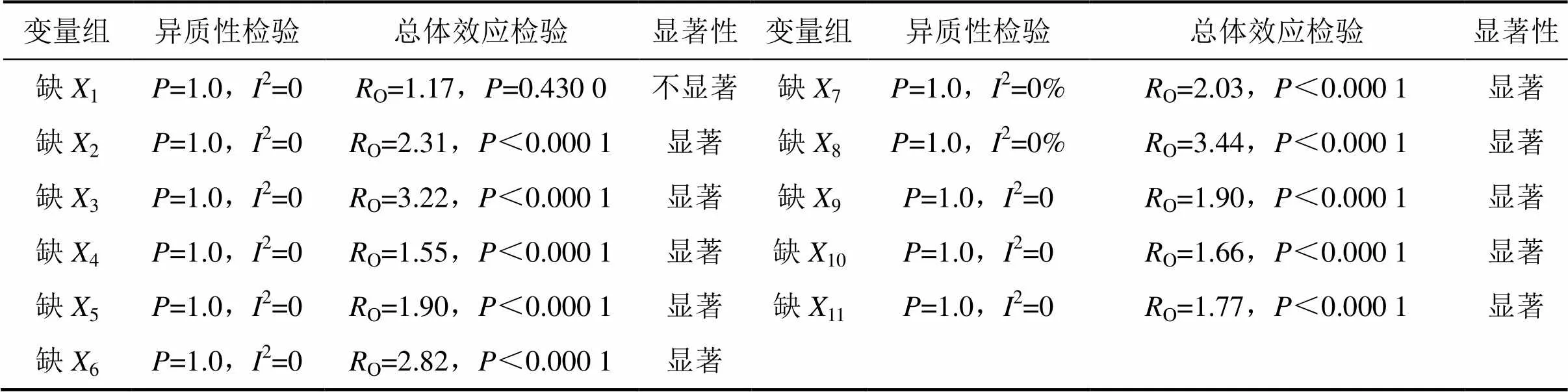
表3 变量组Meta分析的优势比RO及总体效应检验

4 权重分析

模糊综合层次分析法 (fuzzy analytical hierarchy process, FAHP) 是确定权重常用的一种系统分析方法[21−22]。本文采用0.1~0.9标度法构建模糊互补判断矩阵[22−23]。变量的优势比O越大，则其对成矿的贡献程度就越高。因此，可用2个变量之间的优势比O之差来衡量2个变量对于成矿作用的权重。根据表3的数据求得变量两两之差的绝对值如表4所示，用来分析O之差的分布情况。

由表4可知：数据集的O之差最小值为0，最大值为2.27，平均值为0.83，标准差为0.59。根据模糊综合层次分析法的0.1~0.9标度法及其含义，则可判定均值以下区间为稍微重要的标度，均值加1，2和3倍标准差依次对应明显重要、重要得多、极端重要的标度。当两者O之差在(0，0.83 ]之内时“标度”设为0.6；当两者O之差在(0.83，1.42] 之内时“标度”设为0.7；当两者O之差在(1.42，2.01]之内时“标度”设为0.8; 当两者O之差在(2.01，3]之内时“标度”设为0.9。根据表4以及上述O之差标度量化规则，从而可将优势比O转化为权重模糊互补判断矩阵，如表5所示。

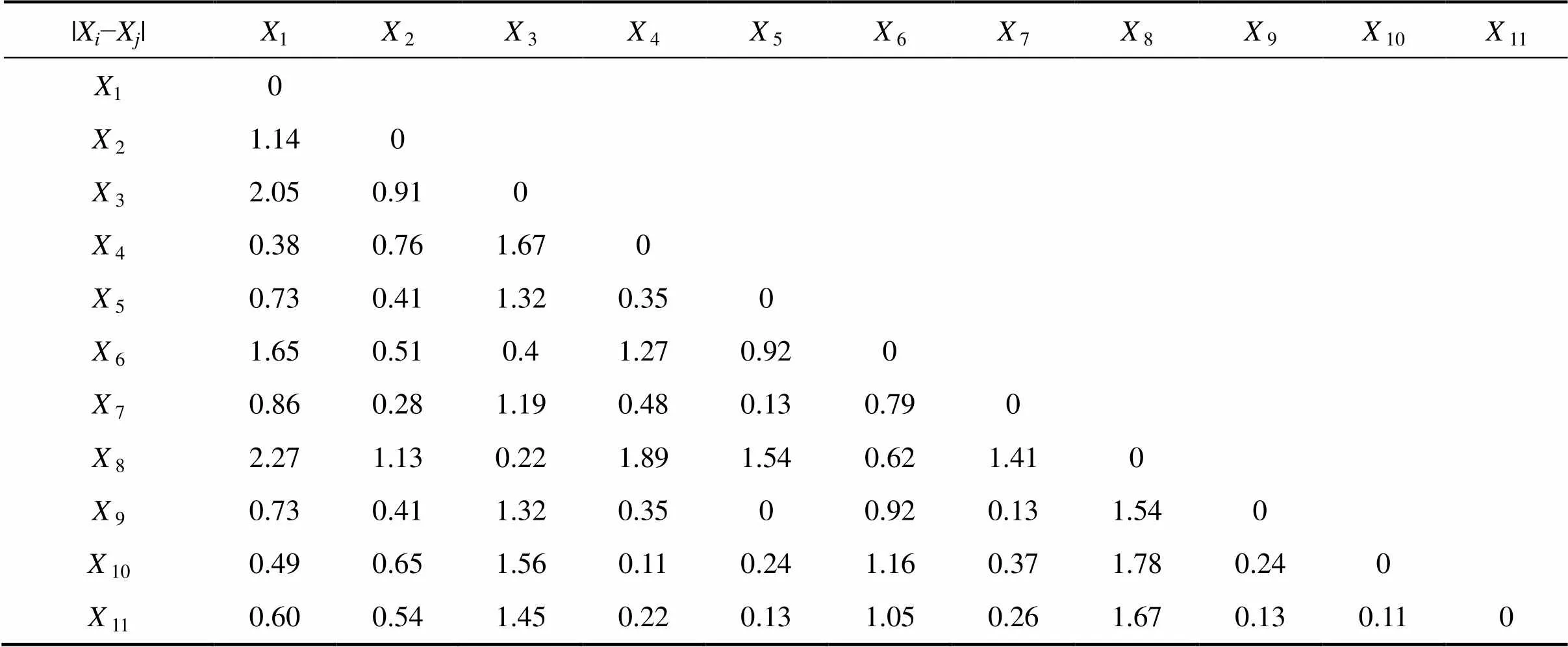
表4 变量RO之差的绝对值统计表

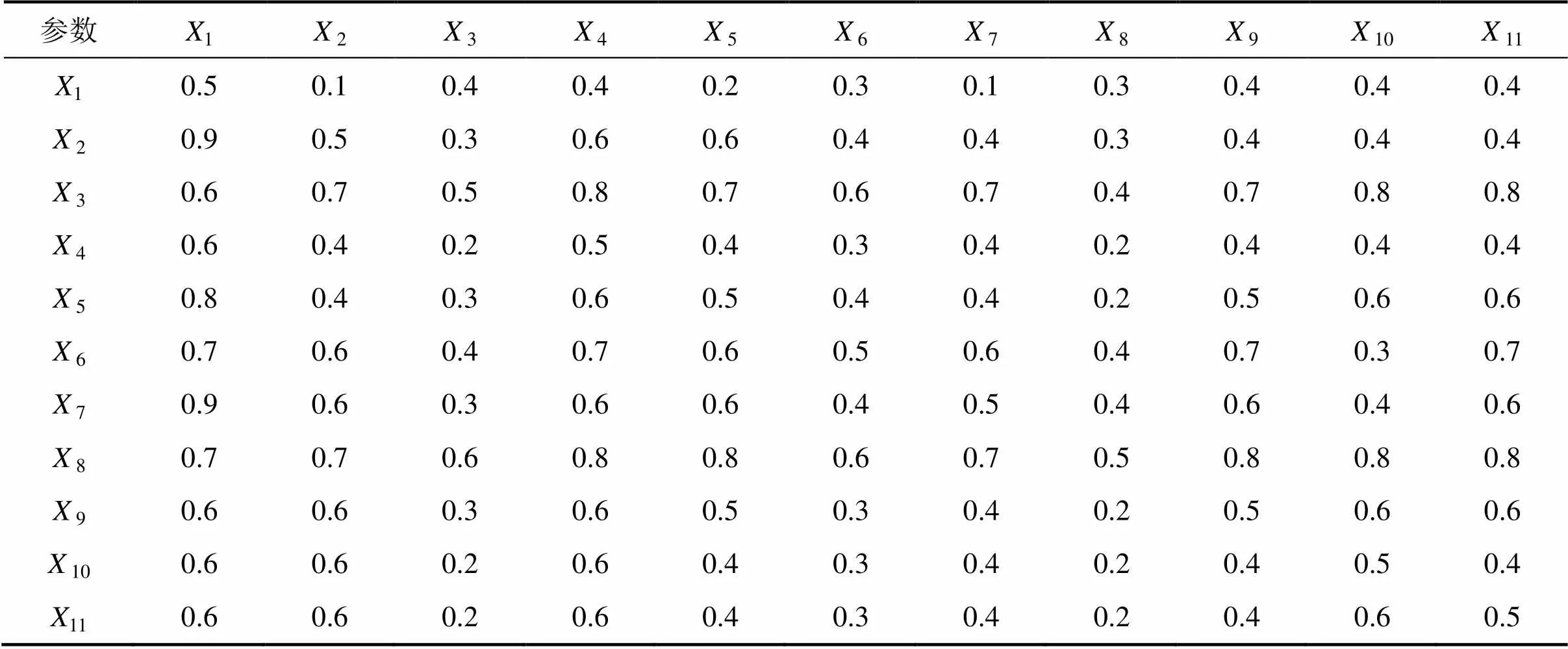
表5 11个变量的权重模糊互补判断矩阵A

利用徐泽水推导的方法[24]，可对模糊互补判断矩阵求解，得到1至11这11个成矿预测变量的权重分别为0.072 7，0.086 3，0.110 0，0.079 0， 0.087 2，0.098 1，0.092 7，0.113 6，0.088 1，0.082 7，0.084 5。根据陈华友等[25]推导的计算方法，利用模糊互补判断矩阵和特征矩阵可求得相容性指数(,*)=0.094 7(小于0.100 0)，可以通过一致性检验，因此，其权重的分配是合理的。

5 成矿有利区

在Meta分析定量确定目标因素权重的基础上，通过网格进行评价单元划分，利用模糊综合评判法(fuzzy comprehensive appraisement, FCA)可对各个单元的成矿有利度进行评价和分级。利用模糊综合评价FCA进行成矿定量预测可归纳为以下几步：1) 建立因素集，如前述的11个成矿预测变量；2) 建立决断集，研究区内的各个单元格的评语即构成决断集；3) 建立单因素评判模糊矩阵；4) 确定权重集；5) 综合评判，对方案集进行隶属度复合运算。根据=·，求得每个网格单元的成矿有利度即综合评价值。预测区范围包括12个1:5万标准图幅，面积约为5 000 km2。与前述规则网格的尺度一致，采用1 km×1 km网格单元进行模糊综合评判和成矿预测。

5.1 评判矩阵

根据地球化学元素和地磁异常特点，可以确定Pb，Zn和F因子及地磁等定量变量的隶属度函数，定性变量的隶属度由专家评分确定，从而可得到评判矩阵。

5.2 成矿有利区

采用加权平均模型对方案集进行隶属度复合运算。根据=·，即可求得每个网格单元的综合评价值即成矿有利度。根据成矿有利度的直方图，可取总体累积频率95%处的作为成矿有利区的临界值[26]。根据累积频率可得到3类成矿有利区的分组区间分别为：一级成矿有利区[0.457 4，0.694 3)；二级成矿有利区[0.325 9，0.457 4)；三级成矿有利区[0.239 1，0.325 9)。

5.3 验证Meta分析

利用北部4个图幅范围内10个区块的矿床(点)资料，以2 km×2 km为网格单元，采用多区域法对基于Meta分析的定量预测法与常规的化探综合异常法的成矿预测效果进行对比分析，得到表6所示的统计结果。基于Meta分析的定量预测法与常规的化探综合异常法所得结果与已知矿(化)点的平均吻合率分别为16.6%和12.2%。

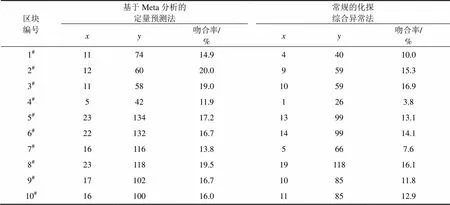
表6 定量预测法与化探综合异常法的预测结果与已知矿(化)点的吻合情况统计表

Meta分析的异质性检验结果为=1.00，大于0.05，可认为多个独立研究具有同质性。森林图中菱形完全位于垂直线右侧，并且假设检验小于0.05，差异具有统计学意义，其优势比O=1.38。Meta分析结果也说明基于Meta分析的定量预测法比与常规的化探综合异常法的找矿预测效果更显著，前者比后者的找矿预测有效性提高36%。

5.4 矿产勘查靶区圈定

研究区内的成矿有利区都是呈北西向展布，与区域构造方向一致，说明矿床受区域断裂构造的控制作用明显。根据成矿有利区的空间分布，可以划分出5个大的成矿远景区：1) 然者涌—色穷弄成矿远景区；2) 耐千—东脚涌成矿远景区；3) 叶龙达—甘藏—东莫扎抓成矿远景区；4) 等群卡—莫海拉亨成矿远景区；5) 吉龙塞—吉那涌成矿远景区。1)~4)成矿远景区主要受羊曲河—襄谦断裂带控制，与区内1:5万水系沉积物化探组合异常较吻合，区内已发现然者涌、东莫扎抓及莫海拉亨等铅锌矿床和几十个矿点。第5)个成矿远景区则主要受控于解曲断裂带，位于1:25万矿产图上铅锌甲级异常区，但在区内1:5万水系沉积物化探组合异常上不明显，区内有少量矿床(点)，遥感的硅化和铁帽异常非常强烈。根据A，B和C这3类勘查靶区的划分方法和原则，基于一、二和三级成矿有利区，综合分析相关资料在5个成矿远景区内，共划分出A类勘查靶区5处，B类勘查靶区10处，C类勘查靶区20处(如表7所示)，可为进一步找矿部署提供依据。

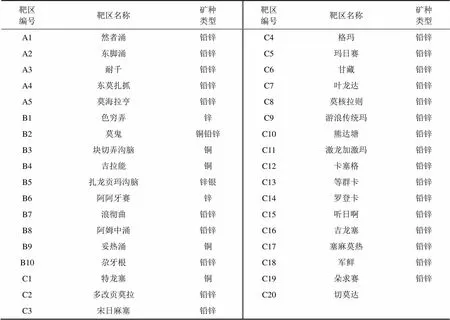
表7 青海杂多地区铜铅锌多金属矿勘查靶区

6 结论

1) 对成矿预测中的各个地质信息变量，利用网格单元法可将地质资料中的非定量数据转化为Meta分析所要求的定量信息，并通过Meta分析可计算不同地质变量的优势比。分析各个变量之间优势比之差，可确定各个地质信息变量对于成矿作用的重要程度，利用模糊综合层次分析法即可求取各个变量在成矿预测中的权重。

2) 对于不精确的、非线性的控矿因素，模糊综合评判模型能有效地量化并揭示出成矿有利度与控矿因素间的模糊关系，在成矿定量定位预测中显示出较好的优越性。

3) 基于Meta分析和模糊综合评判的成矿定量预测模型，在地质勘探数据较丰富的情况下，对成矿预测中地质信息变量权重的确定较客观、合理，采用所建立的成矿定量预测模型取得了较理想的成矿预测效果。但这方面的研究工作尚处于起步阶段，仍需要更进一步研究使之更加方便、快捷和实效。

致谢：感谢青海省地质调查院为本文提供的地质资料。

[1] 成秋明. 非线性矿床模型与非常规矿产资源评价[J]. 地球科学: 中国地质大学学报, 2003, 28(4): 445−455. CHEN Qiuming. Nonlinear mineralization model and information processing methods for prediction of unconventional mineral resources[J]. Earth Science: Journal of China University of Geosciences, 2003, 28(4): 445−455.

[2] PARK N W, CHI K H, KWON B D. Accounting for spatial patterns of multiple geological data sets in geological thematic mapping using GIS based spatial analysis[J]. Environmental Geology, 2007, 51(2): 1147−1155.

[3] 赵鹏大. “三联式”资源定量预测与评价数字找矿理论与实践探讨[J]. 地球科学: 中国地质大学学报, 2002, 27(5): 482−490. ZHAO Pengda. “Three component” quantitative resource prediction and assessments: theory and practice of digital mineral prospecting[J]. Earth Science: Journal of China University Of Geosciences, 2002, 27(5): 482−490.

[4] 侯增谦, 宋玉财, 李政, 等. 青藏高原碰撞造山带PbZnAgCu矿床新类型: 成矿基本特征与构造控矿模型[J]. 矿床地质, 2008, 27(2): 123−144.HOU Zengqian, SONG Yucai, LI Zheng, et al. Thrust controlled, sedimentshosted PbZnAgCu deposits in eastern and northern margins of Tibetan Orogenic Belt: geological features and tectonic model[J]. Mineral Deposits, 2008, 27(2): 123−144.

[5] 彭省临, 王颖, 邵拥军, 等. Meta分析在深部找矿预测研究中的应用[J]. 高校地质学报, 2009, 15(4): 460−469.PENG Shenglin, WANG Ying, SHAO Yongjun, et al. Application of metaanalysis to deep prospecting predictions: an example from the Tongshan copper deposit, Tongling, Anhui Province[J]. Geological Journal of China Universities, 2009, 15(4): 460−469.

[6] 王世称. 综合信息矿产预测理论与方法体系新进展[J]. 地质通报, 2010, 29(1): 1399−1404. WANG Shicheng. The new development of theory and method of synthetic information mineral resources prognosis[J]. Geological Bulletin of China, 2010, 29(1): 1399−1404.

[7] 彭省临, 邵拥军, 张建东. 金属矿山隐伏矿找矿预测理论与方法[J]. 地质通报, 2011, 30(4): 538−543. PENG Shenglin, SHAO Yongjun, ZHANG Jiandong. Prospecting prediction theory and method about concealed oredeposit in metal mine[J]. Geological Bulletin of China, 2011, 30(4): 538−543.

[8] AGTERBERG F P. Computer programs for mineral exploration[J]. Science, 1989, 245(3): 76−81.

[9] CHENG Qiuming, AGTERBERG F P. Fuzzy weights of evidence method and its applications in mineral potential mapping[J]. Natural Resource Research, 1999, 8(1): 27−35.

[10] ERIC V W. Lack’s clutch size hypothesis: an examination of the evidence using metaanalysis[J]. Ecology, 1992, 73(5): 1699−1705.

[11] TONHASCA A, BYRNE D N. The effect of crop diversification on herbivorous insects: a metaanalysis approach[J]. Ecological Entomology, 1994, 19(2): 239−244.

[12] CURTIS P. A metaanalysis of leaf gas exchange and nitrogen in trees grown under elevated carbon dioxide[J]. Plant, Cell and Environment, 1996, 19(1): 127−137.

[13] 王颖, 彭省临, 王雄军. Meta分析在矿集区成矿信息权重值比较中的应用[J]. 中国地质, 2011, 38(1): 180−190. WANG Ying, PENG Shenglin, WANG Xiongjun. Application of oresearching information’weight comparison to the ore concentration area based on metaanalysis[J]. Geology in China, 2011, 38(1): 180−190.

[14] 潘勇, 彭光雄, 刘德波. 基于Meta分析的不同化探异常找矿有效性定量评价[J]. 中南大学学报(自然科学版), 2015, 46(1): 180−187.PAN Yong, PENG Guangxiong, LIU Debo. Quantitative evaluation on prospecting effectiveness of different geochemical anomalies based on metaanalysis[J]. Journal of Central South University (Science and Technology), 2015, 46(1): 180−187.

[15] DEAN C. Resampling tests for metaanalysis of ecological data[J]. Ecology, 1997, 78(5): 1277−1283.

[16] 刘关键, 吴泰相, 康德英. Meta分析中的统计学过程[J]. 中国临床康复, 2003, 7(4): 538−539. LIU Guanjian, WU Taixiang, KANG Deying. The statistical process of metaanalysis[J]. Modern Rehabilitation, 2003, 7(4): 538−539.

[17] 赵宁, 俞顺章. Metaanalysis: 一种新的定量综合方法[J]. 中国慢性病预防与控制, 1993, 1(6): 277−281. ZHAO Ning, YU Shunzhan. Meta analysis: a new quantitative approach to research synthesis[J]. Chinese Journal of Prevention and Control of Chronic Noncommunicable Diseases, 1993, 1(6): 277−281.

[18] 黄鲁众, 杨腾飞, 黄晶晶, 等. 高温作业对工人心电图影响的Meta分析[J]. 中国循证医学杂志, 2011, 11(2): 174−180. HUANG Luzhong, YANG Tengfei, HUANG Jingjing, et al. ECG changes in workers exposed to hightemperature: a metaanalysis[J]. Chinese Journal of Evidence Based Medicine, 2011, 11(2): 174−180.

[19] 陈进, 毛先成, 彭省临, 等. 物化探技术有效性定量评价方法研究: 以凤凰山铜矿CSAMT 法为例[J]. 大地构造与成矿学, 2010, 34(2): 263−269.CHEN Jin, MAO Xiancheng, PENG Shenglin, et al. Quantitative evaluation on availability through geophysical and geochemical prospecting techniques: a case study on CSAMT approach in Fenghuangshan copper deposit[J]. Geotectonica et Metallogenia, 2010, 34(2): 263−269.

[20] 彭省临, 樊俊昌, 邵拥军, 等. 矿山深部隐伏矿定位预测关键技术新突破[J]. 中国有色金属学报, 2012, 22(3): 844−854.PENG Shenglin, FAN Junchang, SHAO Yongjun, et al. New breakthrough in key technologies of location prediction about deep concealed ore bodies of mine[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(3): 844−854.

[21] 徐泽水. 一种改进的模糊一致性判断矩阵构造方法[J]. 应用数学与计算数学学报, 1996, 11(2): 62−71. XU Zeshui. A improved method for constructing judgment matrix with fuzzy consistency[J]. Communication on Applied Mathematics and Computation, 1996, 11(2): 62−71.

[22] 张吉军. 模糊层次分析法(FAHP)[J]. 模糊系统与数学, 2000, 14(2): 80−89. ZHANG Jijun. Fuzzy analytical hierarchy process[J]. Fuzzy Systems and Mathematics, 2000, 14(2): 80−89.

[23] 姬东朝, 宋笔锋, 喻天翔. 模糊层次分析法及其在设计方案选优中的应用[J]. 系统工程与电子技术, 2006, 28(11): 1692−1696. JI Dongchao, SONG Bifeng, YU Tianxiang. FAHP and its application in the selection of design scheme[J]. Systems Engineering and Electronics, 2006, 28(11): 1692−1696.

[24] 徐泽水. 模糊互补判断矩阵排序的一种算法[J]. 系统工程学报, 2001, 16(4): 311−314. XU Zeshui. Algorithm for priority of fuzzy complementary judgment matrix[J]. Journal of Systems Engineering, 2001, 16(4): 311−314.

[25] 陈华友, 赵佳宝. 模糊判断矩阵的相容性研究[J]. 运筹与管理, 2004, 13(1): 44−47. CHEN Huayou, ZHAO Jiabao. Research on compatibility of fuzzy judgment matrices[J]. Operations Research and Management Science, 2004, 13(1): 44−47.

[26] 韩春明. 应用模糊评判法预测东准噶尔地区金成矿有利区[J]. 新疆工学院学报, 1996, 17(3): 168−173. HAN Chunming. The application of fuzzy discrimination to locate east junger gold ore advantageous prognostic region[J]. Journal of Xinjiang Institute of Technology, 1996, 17(3): 168−173.

Metallogenic prediction based on meta-analysis in Zaduo, Qinghai Province

PAN Yong1, 3, PENG Shenlin1, PENG Guangxiong1, 2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. State Key Laboratory for Continental Tectonics and Dynamics, Beijing 100037, China; 3. College of Tan Kah Kee, Xiamen University, Xiamen 363105, China)

To reduce the uncertainty of weight determination, meta-analysis of evidence-based medicine was used in the quantitative prediction of mineral resource in Zaduo, Qinghai Province. Based on the analysis of the regional metallogenic regularity and ore controlling factors, 11 predictors of six elements such as formation, structure, magmatite, geomagnetic anomaly, geochemical anomaly and remote sensing alteration were selected to construct the index system of quantitative prediction. Based on grid unit, more than 50 deposits and ore occurrences in study area were used as test samples to count the superposition of the spatial position between 11 predictors and deposits. According to the statistic results, the non-quantitative geological data could be converted to quantitative information required by meta-analysis and the odds ratio (O) of 11 predictors could also be derived. Through the analysis of the difference of odds ratio value of 11 predictors, their weights for metallogenic prediction could be calculated based on fuzzy analytical hierarchy process (FAHP). Combined the above weights with fuzzy comprehensive appraisement (FCA), a quantitative prediction model of Pb-Zn deposits in Zaduo, Qinghai Province, could be constructed. Three classes’ favorable areas of ore-forming were zoned based on the ore-forming favorability derived from FCA model. 5 mineralization prospecting zones have been schemed, which includes 5 of A-grade exploring targets, 10 of B-grade exploring targets and 20 of C-grade exploring targets. The results show that the prospecting effectiveness of this quantitative prediction model based on meta-analysis is higher 36% than that of comprehensive geochemical anomaly model.

meta-analysis; concealed orebody; fuzzy comprehensive appraisement; quantitative prediction

10.11817/j.issn.1672-7207.2016.09.025

P612；P208

A

1672−7207(2016)09−3093−08

2016−02−10；

2016−04−15

国家自然科学基金资助项目(41403035)；中国博士后科学基金资助项目(2012T50832)；大陆构造与动力学国家重点实验室开放基金资助项目(K201504) (Project(41403035) supported by the National Natural Science Foundation of China; Project(2012T50832) supported by the China Postdoctoral Science Foundation; Project(K201504) supported by the Open Foundation of State Key Laboratory of Continental Tectonics and Dynamics)

彭光雄，博士，讲师，从事遥感地质与成矿预测研究；E-mail: pgxcsu@csu.edu.cn

(编辑 陈灿华)