基于MATLAB的倒立摆特征根灵敏度分析

钱苇航 闻新

摘要：倒立摆是一个复杂的非线性系统，是进行各种控制理论教学及验证先进控制理论的理想平台。本文根据特征根灵敏度分析理论，提出了一种倒立摆控制系统特征根的分析与设计方法，利用MATLAB绘制倒立摆控制系统的根轨迹，得到增益变化对特征根灵敏度的影响。最后，通过在根轨迹上选择合适的增益和特征根，满足系统设计的要求。

Abstract： The inverted pendulum is a complicated system， which is an ideal platform to carry out all kinds of control theory and teach and check out controlled experiment. According to the concept of characteistic roots' sensitivity， the method of using characteistic roots' sensitivity to analyze the inverted pendulum system is introduced. Then， MATLAB is used to draw the inverted pendulum's root locus， the effect of the gains'changes to sensitivities of the characteristic roots are found. Finally， we can choose appropriated gain and characteistic root to realize required function in the root locus.

关键词：倒立摆；特征根；灵敏度；控制系统

Key words： inverted pendulum；characteistic root；sensitivity；control system

中图分类号：TP273 文献标识码：A 文章编号：1006-4311（2016）09-0206-03

0 引言

通常，自动控制系统是指由控制器、被控对象和敏感器组成的系统。自动控制系统的特征是在控制信息作用下，改变被控对象的运动或进入各种状态。但是，由于外界環境干扰往往引起自动控制系统参数改变，从而导致自动控制系统性能也跟着变化。而灵敏度就是外界变化对系统性能影响的一种度量。由于实际应用中有些控制系统的数学模型非常复杂，使我们难以对系统的鲁棒性进行分析，但是如果运用MATLAB软件来绘制系统的根轨迹图形，就会使我们的分析变的简便的多[1-2]。本文利用MATLAB绘制倒立摆模型的根轨迹，分析随着系统增益的变化，倒立摆模型的特征根灵敏度会发生怎样的改变。

1 建立系统传递函数与特征根灵敏度

1.1 一级倒立摆系统的动力学方程和传递函数

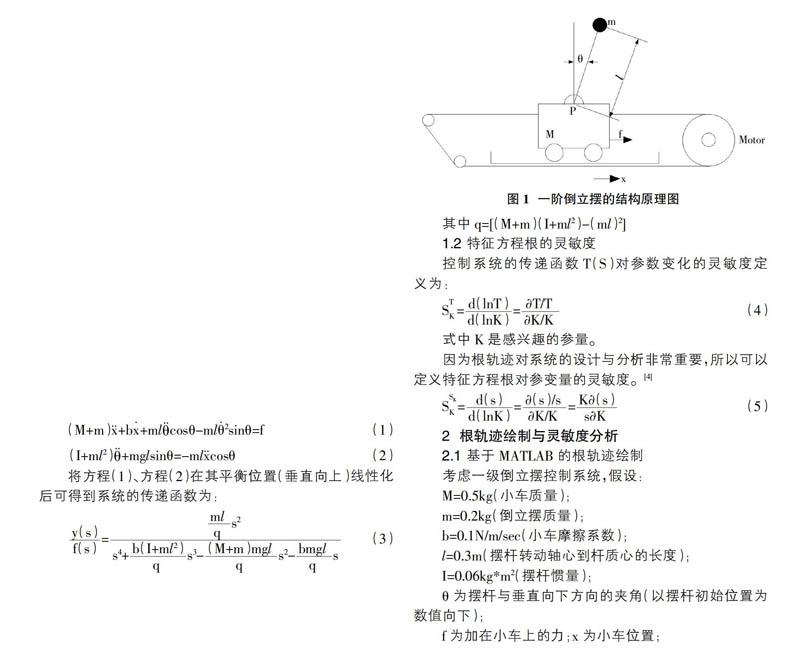
图1为一级倒立摆系统，假设M为小车质量，m为摆杆质量，b为小车摩擦系数，l为摆杆转动轴心到杆质心的长度，I为摆杆惯量，f为加在小车上的力，x为小车位置，θ为摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）。忽略了空气流动和摩擦的影响，利用牛顿定律得到系统的运动方程为

（M+m）■+b■+ml■cosθ-ml■2sinθ=f（1）

（I+ml2）■+mglsinθ=-ml■cosθ （2）

将方程（1）、方程（2）在其平衡位置（垂直向上）线性化后可得到系统的传递函数为：

■=■ （3）

其中q=[（M+m）（I+ml2）-（ml）2]

1.2 特征方程根的灵敏度

控制系统的传递函数T（S）对参数变化的灵敏度定义为：

S■■=■=■（4）

式中K是感兴趣的参量。

因为根轨迹对系统的设计与分析非常重要，所以可以定义特征方程根对参变量的灵敏度。[4]

S■■=■=■=■（5）

2 根轨迹绘制与灵敏度分析

2.1 基于MATLAB的根轨迹绘制

考虑一级倒立摆控制系统，假设：

M=0.5kg（小车质量）；

m=0.2kg（倒立摆质量）；

b=0.1N/m/sec（小车摩擦系数）；

l=0.3m（摆杆转动轴心到杆质心的长度）；

I=0.06kg*m2（摆杆惯量）；

θ为摆杆与垂直向下方向的夹角（以摆杆初始位置为数值向下）；

f为加在小车上的力；x为小车位置；

Y为摆杆与垂直向上方向的夹角，

则传递函数方程（3）为

■=■（6）

由方程（6），求得特征方程为

1+■=0 （7）

当K从0变化到∞时，通过MATLAB方程（7）的根轨迹，仿真程序如下：

num1=4.545*[1 0 0]；

den1=[1 0.1818 -31.18 -4.455 0]；

mysys1=tf（num1，den1）；

subplot（2，1，1）；

rlocus（mysys1）

title（'倒立摆模型的根轨迹图形'）；

[k，ploes]=rlocfind（mysys1）

运行程序，得到如图2所示根轨迹。

■

2.2 特征根对K的灵敏度分析

实现系统在受到外界变化的影响之后，仍能保持某些性能的特性，必须使特征根对参数变化的影响不敏感，即要求灵敏度满足一定的要求。

利用MATLAB得到如图3所示的增益K=6.62，s=

-0.989±1.22i。當K=6.02时，s=-1.24±0.613i，如图4所示。对两者进行分析：

Δs=-1.24+0.613i-（-0.989+1.22i）

=-0.251-0.607i （8）

■=■=-0.09 （9）

S■■=■=■=7.2∠67°（10）

同理可以找到K=7.22时，s=-0.73±1.72i。

Δs=-0.729+1.72i-（-0.989+1.22i）

=0.26+0.5i （11）

■=■=0.09 （12）

S■■=■=■=6.3∠63° （13）

可以看出当增益变化时，灵敏度大小和角度近似相等：

S■■=S■■ （14）

∠S■■=∠S■■ （15）

即■=0成立。由文献[5]可以知道在选择系统特征根的时候为了保持系统的稳定性应该选择对增益不灵敏的特征根。将控制系统在一定参数的摄动下，维持某些性能的特性称为鲁棒性。如果在实际运用中，系统满足方程（14）和方程（15），则称系统对增益变化具有鲁棒性。

3 结束语

本文首先通过MATLAB绘制倒立摆的根轨迹，使系统的分析变得简单的多，节省了很多精力和时间[2-3]。再经过对系统的特征根灵敏度分析，得到了增益变化不大时灵敏度间的关系，通过选择合适的特征根，来满足控制系统的设计要求。

参考文献：

[1]闻新，等.MATLAB基础与范例教程[M].国防出版社，2013.

[2]黄忠霖.自动控制原理的MATLAB实现[M].北京：国防工业出版社，2007.

[3]毕开波，王晓东，刘智平.飞行器制导与控制及其仿真技术[M].北京：国防工业出版社，2009.

[4]赵阳，等.基于的特征根灵敏度分析[J].工业控制计算机，2012，2：69-72.

[5]I.J Nagrath，M.Gopal .Control Systems Engineering[M]. Halsted Press，aDivision of John Willey& Sons，inc.1982.