经典控制理论在飞行控制系统中的设计应用

刘伯健

摘要：飞行控制系统对控制飞机起到了至关重要的作用。飞行控制系统可用来保证飞行器的稳定性和操纵性、提高完成任务的能力与飞行品质、增强飞行的安全及减轻驾驶员负担。然而如何设计闭环飞行控制系统的反馈参数，使此系统能拥有良好的动态特性和飞机控制力。本文以F16飞机模型为例，以经典控制理论中的根轨迹法为切入点，运用MATLAB软件进行仿真分析设计，最终设计闭环飞行控制系统的反馈参数。

Abstract： Flight control system has played a vital role in controlling the flight. Flight control system can be used to guarantee stability and maneuverability of aircraft， improve the ability of completing the task and flying qualities， enhance flight safety and reduce the burden of the pilot. However， how to design the closed-loop feedback parameters of flight control system can make the system has good dynamic characteristics and good ability of controlling the plane. This article takes F16 airplane model as an example. Based on the root locus method for classical control theory， the author finally designs a closed-loop feedback parameters of flight control system by using the MATLAB software simulation.

关键词：经典控制理论；飞行控制系统；自动控制

Key words： classical control theory；flight control system；automatic control

中图分类号：V249.1 文献标识码：A 文章编号：1006-4311（2016）09-0151-04

0 引言

飞行控制系统是对飞机姿态进行控制的系统，此系统动态性能的优良与否是控制飞机稳定飞行的关键所在。随着飞行器的不断进步，对飞行控制系统的要求也不断提升，各国对飞行控制系统的改进研究也在不断前进。文章从经典控制理论的根轨迹法出发，对飞行控制系统的反馈参数进行设计并运用MATLAB进行仿真验证。

经典控制理论是建立在频率响应法和根轨迹法基础上。经典控制理论的研究对象是单输入、单输出的控制系统。经典控制理论的特点是以输入输出特性为系统数学模型，采用频率响应法和根轨迹法等图解分析方法，分析系统性能和设计控制装置。虽然现在出现了现代控制理论，可是经典控制理论在自动控制系统的设计上，仍占有着不可替代的位置。下面我们就以经典控制理论设计F16飞机的控制反馈系统，并以MATLAB进行仿真验证。

飞机可以分为两个控制面，横向控制面和纵向控制面，两个控制面存在耦合和相互作用。但是本文此次设计仅针对于忽略横纵向耦合并且线性化配平过后的开环F16飞機系统，力求得到一个比较完美的动态响应特性，使系统达到超调量小于百分之五，调节时间小于3s的良好动态特性，并尽量减小荷兰滚模态的系数的闭环飞行控制系统。

由于飞机在不同飞行高度、飞行速度的配平参数不同（即状态矩阵不同），所以本文仅就F16在3500m，150m/s的状态配平下进行飞机横向反馈系统设计（配平已知）。

飞机横向反馈系统设计：

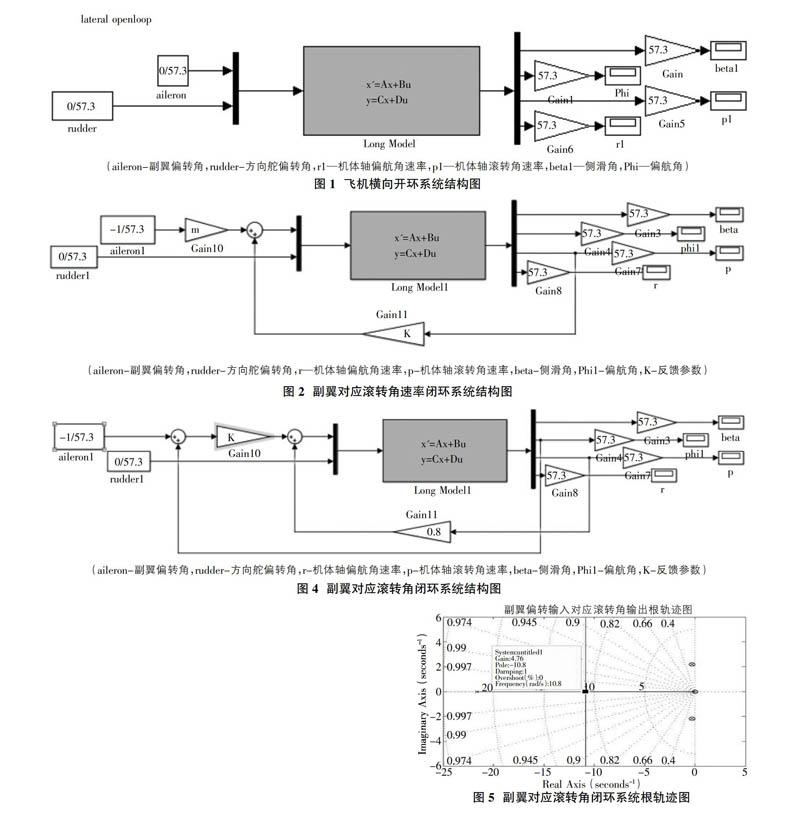
如图1所示，对于飞机横向系统来说，此系统是二输入四输出的系统。构建simlink结构图，出于简化问题的考虑，我们只研究副翼偏转对应滚转角系统和方向舵偏转对应航向角系统的反馈线路设计。首先我们先研究副翼偏转对应滚转角系统的反馈设计。

1 副翼偏转对应滚转角系统的反馈设计

与方向舵—俯仰角系统一样，我们需要先调节好副翼偏转对应滚转角速度系统的动态特性。方案如下：

①副翼偏转对应滚转角速度系统的反馈设计。

如图2所示，运用Simulink中Gain环节构建反馈线路，图中的K就是我们需要确定的反馈参数，因此我们需要得到副翼对应滚转角速率系统的开环传递函数：

G=■

根据开环传递函数绘制出根轨迹图（图3）。

■

如图3根轨迹图可看出，传递函数共有四个极点：p1，p2对应荷兰滚模态；p3对应滚转模态；p4对应螺旋模态。随着K值的增大，极点p3左移，滚转角速率对应阶跃响应的调节时间减小，系统动态特性更好；但当K>0.138时，随着K的增大，荷兰滚模态对应的阻尼比减小，荷兰滚运动较剧烈，因此，在满足一定动态性能要求时要使K尽量小。

经调试发现当K=0.8时，调节时间为0.108s，超调量为5%，系统动态特性较好，且K值较小，荷兰滚运动尚可。不妨选取k=0.8。以此为基础，进行副翼偏转对应滚转角系统的反馈设计。

2 副翼偏转对应滚转角系统的反馈设计

如图4所示副翼对应滚转角闭环系统结构图中的K即是我们需要确定的反馈参数，内环即是上述内容设计出来的副翼偏转对应滚转角速度系统。首先我们得到副翼对应滚转角闭环系统的开环传递函数：

G=■

根据开环传递函数绘制出系统根轨迹图（图5）。

从图5中我们不难发现，这是一个3零点5极点的根轨迹图，其中有三对零极点互相消去，剩下两个极点对系统产生重要影响（即振荡环节根轨迹）。我们不妨取K=4.75，由经典控制理论系统此时应有最好的动态特性。

当K=4.75时，系统超调量为1.12%，调节时间为0.49s，滚转角对应副翼偏转响应动态性能最好，同时满足设计指标，荷兰滚模态参数尚可。所以我们选取K=4.75。至此副翼对应滚转角闭环系统反馈设计结束。

下面我们对横向面第二个系统进行反馈设计。

3 方向舵对应偏航角系统反馈设计

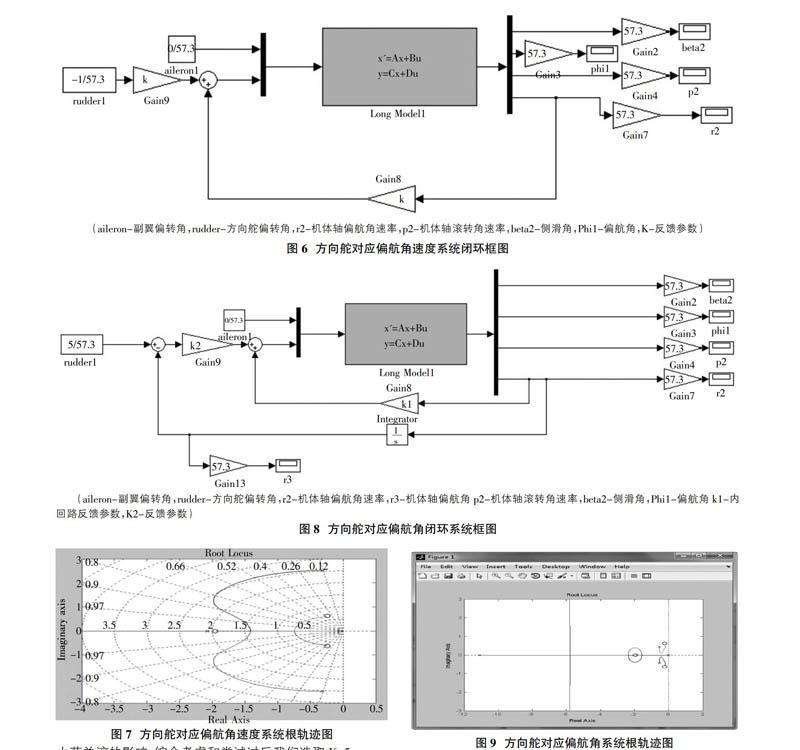
3.1 方向舵对应偏航角速度系统

首先我们得到其开环系统传递函数：

G=■

通过开环传递函数，我们可以画出根轨迹图（图7）。

由图7所示由于系统响应的主要根轨迹是实轴上的根轨迹，所以显而易见系统的K值越大动态特性也就越好，但是由于需要减小荷兰滚模态的影响，k应该在1.92到3.17左右。两个参量相互影响，所以我们不妨设定个参数：超调量不得超过百分之五，调节时间不得超过3s，同时尽可能减小荷兰滚的影响，综合考虑和尝试过后我们选取K=5。

3.2 方向舵对应偏航角系统

根据上述内容，在偏航角速度的测速反馈系统中，我们采取K1=5作为反馈系数，在此基础上我们进行偏航角系统的反馈参数设计。

首先我们根据系统图8推导出传递函数：

G=■

根据传递函数绘制出根轨迹图：

从图9中我们不难发现，这是一个3零点5极点的根轨迹图，其中有三对零极点互相消去，剩下两个极点对系统产生重要影响（即振荡环节根轨迹）。K2较小时，根轨迹处于过阻尼状态，调节时间较大；K2较大时，处于欠阻尼状态，系统超调量会增大，所以我们不妨取K2=12.3（震荡环节交点），系统理论应有最好的动态特性。

從上图不难看出，当K2<12.3时，调节时间会增加，超调量小。当k2>12.3时，调节时间缩小，但是会有大超调量产生。所以我们选取K2=12.3作为我们的方向舵对应偏航角系统的反馈参数时，满足设计指标。至此方向舵对应偏航角系统反馈设计结束。此时飞机控制系统在互不影响的前提下，运用如上反馈网络，系统的动态特性满足超调量不大于5%，调节时间不大于3S的指标。

4 结语

以上方法，是运用根轨迹法，对飞行横向控制面反馈系统进行参数设计。根轨迹法作为经典控制理论重要的一部分，在飞行控制上的应用远不止如此。在现代控制理论飞速发展的今天，经典控制理论以其独特的魅力，仍在飞行控制方面发挥着不可忽视的作用。

参考文献：

[1]郑超.基于MATLAB的根轨迹法的研究[J].山西师范大学学报（自然科学版），2008，S2：29-34.

[2]卢京潮，赵忠，刘慧英，袁冬莉，贾秋玲.自动控制原理[M]. 北京清华大学出版社，2008.

[3]贾秋玲，袁冬莉，栾云凤.基于MATLAB7.X/Simulink/Stateflow系统仿真.分析及设计[M].西安西北工业大学出版社，2006.