借助“旁白”透析法则本质

李伯敏

一、教材分析

有理数的加法是有理数运算的重要基础之一，它是整个初中代数的基础，直接关系到有理数的运算、实数运算、代数式运算、解方程、研究函数等内容的学习。有理数的意义是本章的基础，有理数的运算是本章的重点，有理数的混合运算是本章的难点。有理数的加法是学生学习的第一种有理数运算，学生能否接受和形成在有理数范围内进行的各种运算的思考方式是这一节课学习的关键。这种思考方式正是教材旁白提出的“先定符号，再算绝对值”，所以这节课的核心将围绕这个关键点展开。

二、学情分析

本节课是初一新授课，学生已经在小学时已经学习了正数与正数相加、正数与0相加，引入负数后，有理数的加法就还有负数与负数相加、负数与正数相加、负数与0相加这几种情况。所以本节课在学生已有的基础上从文字、数轴、算式三个角度探求有理数加法法则，借助教材“旁白”透析有理数加法的核心本质。在教学中通过独立思考、自主探索、合作交流等基本数学活动，促使学生理解并掌握相应的数学知识与技能，产生积极的情感体验，进而创造性地解决问题，有效地发展了学生的思维能力。

教学目标（略），教学重点难点（略）。

三、教学环节

（一）从不同角度看有理数加法

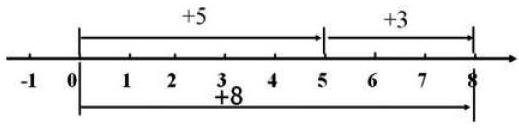
1.先向东走5个单位，再向东走3个单位，一共向东走了8个单位。

我们以原点为起点，规定向东为正，向西为负，我们可以利用数轴分析这一过程（展示数轴图）。借助数轴我们容易得到算式①（+5）+（+3）=+8。

2.先向西走5个单位，再向西走3个单位，一共向西走了8个单位。我们可以利用数轴分析这一过程（展示数轴图）。借助数轴我们容易得到算式②（-5）+（-3）=-8。

（二）借助“旁白”研读有理数加法法则1

观察算式①、算式②，我们可以发现这两个算式属于同号两数相加，借助教材旁白“先定符号，再算绝对值”，可以得出有理数的加法法则1。同号两数相加：取相同的符号，并把绝对值相加。举例：（-3）+（-9）先确定符号，符号为负，再把绝对值相加，3+9=12，所以结果为-12。

（三）变换角度看有理数加法

3.先向东走5个单位，再向西走3个单位，此时在原点东侧2个单位处。我们可以列出算式③（+5）+（-3）=+2，教材旁白中提到“你能用數轴表示算式③吗？”我们一起来试一下（展示数轴图）。

4.先向东走3个单位，再向西走5个单位，此时在原点西侧2个单位处。我们可以列出算式④（+3）+（-5）=-2，教材旁白中提到“你能用数轴表示算式④吗？”我们一起来看一下（展示数轴图）。

（四）借助“旁白”研读有理数加法法则2

观察算式③、算式④，我们可以发现这两个算式属于异号两数相加，并且绝对值不相等，借助教材旁白“先定符号，再算绝对值”，可以得出有理数的加法法则2。绝对值不相等的异号两数相加：取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。举例：（-6）+2确定符号，符号为负，在用较大的绝对值减去较小的绝对值，6-2=4，所以结果为-4。

（五）从不同的角度看特殊的有理数加法

5.先向东走5个单位，再向西走5个单位，此时在原点。我们可以借助数轴分析这一过程（展示数轴图），得到算式⑤（+5）+（-5）=0。

6.先向西走5个单位，再向东走0个单位，此时在原点西侧5个单位处。我们可以借助数轴分析这一过程（展示数轴图），得到算式⑥（-5）+ 0 = -5。

（六）特殊的有理数加法法则

（+5）+（-5）=0，我们可以发现：互为相反数的两个数相加得0。（-5）+0=-5，我们可以发现：一个数同0相加，仍得这个数。

（七）有理数加法法则

展示有理数加法法则：

1.同号两数相加，取相同的符号，并把绝对值相加。

2.绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。

3.互为相反数的两个数相加得0。

4.一个数同0相加，仍得这个数。

我们把它分成1.同号两数相加，2.绝对值不相等的异号两数相加，3.互为相反数的两个数相加，4.一个数同0相加。对于法则1和法则2，特别注意教材旁白提到“先定符号，再算绝对值”。在学习过程中并不需要死记硬背，而是借助教材“旁白”理解了法则的本质，化繁为简，深入浅出。

四、教学反思

本节课主要讲解有理数加法法则的发现和归纳。分别从文字、数轴、算式三个不同角度探索有理数加法法则的生成过程，并借助教材“旁白”变换角度再次研读和分析，理解有理数的加法法则的本质问题是确定符号与绝对值的问题。通过边分析边举例的方法，进一步阐述如何正确运用法则进行有理数的加法运算。

有理数加法法则中共包括两种情形，即同号两数相加和异号两数相加，涉及到和的符号的确定和绝对值的确定。在教学过程中，引导学生学会关注教材，借助教材旁白“先定符号，再算绝对值，深入透析文字语言背后的数学问题的核心本质。先确定符号的问题，会发现算绝对值就是小学的加减法问题，体会化未知为已知的化归思想，体会参与过程的乐趣与收获知识的喜悦，注重培养学生发展核心素养。

对于法则3互为相反数的两个数相加得0和法则4一个数同0相加，仍得这个数，这两个法则与法则1和法则2相比较更浅显易懂，一目了然。本节课单独讲解这两个法则，特别是把法则3从法则2中分离出来，主要是为了减轻学生在理解法则2上的负担。法则2文字繁多并且是本节课的重点和难点，分别讲解后，学生不仅可以对比法则1理解法则2，还可以更深入地挖掘有理数加法法则的本质。