引以为戒事半功倍

葛亚美

引以为戒事半功倍

葛亚美

同学们，在全等三角形的章节学习中，有没有总是犯一些意想不到的错误呢？以下是你们的学长学姐们做错的题，你能知道他们为什么错了吗？

例1下列说法中，正确的有（）.

①三角对应相等的两个三角形全等；②三边对应相等的两个三角形全等；③两角一边相等的两个三角形全等；④两边一角对应相等的两个三角形全等.

A.1个B.2个

C.3个D.4个

【错解】选C.

【正解】选A.

【分析】①“AAA”不能判定两三角形全等，故不正确；③必须是两角一边对应相等的两个三角形全等，所以③的结论错误；④必须是两边和一夹角对应相等的两个三角形全等，故④的结论也错误；根据“SSS”可知②能证明两个三角形全等.故选A.

【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：“SAS”“ASA”“AAS”“SSS”“HL”，注意：“SSA”“AAA”不能判定两个三角形全等，“对应”两字很重要.

例2下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是（）.

A.①②B.②③

C.①③D.①②③

【错解】选D.

【正解】选A.

【分析】①正确.可以用“AAS”或者“ASA”判定两个三角形全等；②正确.可以用“倍长中线法”和“SSS”定理，判定两个三角形全等；③不正确，因为第三条边上的高可能在三角形的内部，也可能在三角形的外部，也就是说，这个三角形可能是锐角三角形，也可能是钝角三角形，所以就不全等了.故选A.

【点评】本题同样考查全等三角形的判定方法，要根据已知条件逐个分析，看是否符合全等三角形的判定方法.

例3下列说法中，错误的是（）.

A.底边和顶角分别相等的两个等腰三角形全等

B.含有100°内角且腰长是3cm的两个等腰三角形全等

C.腰长和底边长分别对应相等的两个等腰三角形全等

D.含有80°内角且腰长是3cm的两个等腰三角形全等

【错解】选B.

【正解】选D.

【分析】A可用“AAS”或“ASA”证明全等；B中含有100°内角的等腰三角形，100°的角一定是顶角，可用“SAS”证明全等；C可用“SSS”证明全等；D中含有80°内角的等腰三角形，80°的角不确定是顶角还是底角.故选D.

【点评】本题考查全等三角形的判定和等腰三角形的性质.

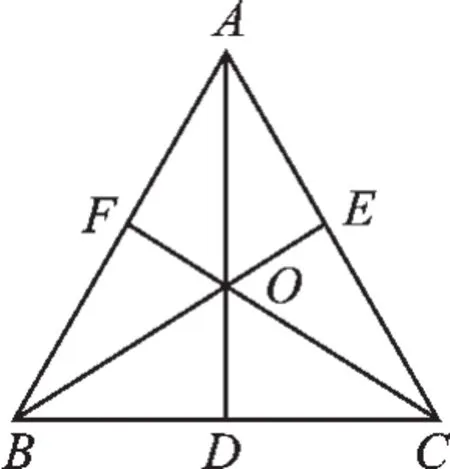
图1

例4△ABC中，AB= AC.三条高AD、BE、CF相交于O，如图1所示.那么右图中全等的三角形有（）.

A.5对B.6对C.7对D.8对

【错解】B.

【正解】C.

【分析】首先根据已知条件，用“HL”证明△ADB≌△ADC，进而依次根据“SAS”“ASA”“SAS”“SSS”“SAS”证明其他三角形全等，共7对，注意要做到不重不漏.具体步骤：

∵AB=AC，AD是高，

∴BD=CD，又AD=AD，∠ADB=∠ADC=90°，

∴△ADB≌△ADC，∴△ODC≌△ODB；

同理有：△COE≌△BOF，△AOC≌△AOB，

△AOE≌△AOF，△CBE≌△BCF，

△ACF≌△ABE.

共7对.故选C.

【点评】做题时要从已知条件出发，结合图形，利用全等的判定方法由易到难逐个寻找.

例5如图2，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F.若AC=BD，AB= ED，BC=BE，则∠ACB等于（）.

图2

A.∠EDB

B.∠BED

D.2∠ABF

【错解】选B.

【正解】选C.

【分析】在△ABC和△DEB中，AC=BD，AB= ED，BC=BE，∴△ABC≌△DEB（SSS）.

∴∠ACB=∠DBE.∵∠AFB是△BFC的外角，

故选C.

【点评】本题利用了全等三角形的判定方法和性质、三角形外角的性质.

例6已知△ABC与△DEF全等，∠A=∠D=90°，∠B=37°，则∠E的度数是（）.

A.37°B.53°

C.37°或63°D.37°或53°

【错解】选A.

【正解】选D.

【分析】在△ABC中，∠C=180°-∠A-∠B=53°.

∵△ABC与△DEF全等，

∴当△ABC≌△DEF时，∠E=∠B=37°；

当△ABC≌△DFE时，∠E=∠C=53°.

故∠E的度数是37°或53°.故选D.

【点评】本题考查了全等三角形的性质，由于题中没有明确对应关系，故应分类讨论.

（作者单位：江苏省扬州大学附属中学东部分校）