台风环境下海上结构的设计风浪联合概率模型

陈忆前，陈艾荣，马如进

(1.同济大学　土木工程学院，上海　200092;2.招商局重庆交通科研设计院有限公司，重庆　400067)



台风环境下海上结构的设计风浪联合概率模型

陈忆前1,2，陈艾荣1，马如进1

(1.同济大学土木工程学院，上海200092;2.招商局重庆交通科研设计院有限公司，重庆400067)

为了研究作用于海上结构的主要极端作用，以短期测波资料为基础，将对海浪形成发展有重要影响的风速与波高、周期有机结合起来，推导出给定风速条件下的波高、周期联合概率分布模型，对波高、风速相关系数进行参数分析。将给定风速条件下N年最大波高作为滤过复合Poisson过程考虑，推导了其超值累积分布，进而反推台风时相应重现期下的年最大波高众值及相应特征周期，得出了基于台风环境的设计波浪要素。结果表明：推导模型从概率学角度建立了风、浪设计因素的对应关系，简化了传统设计参数的计算。

桥梁工程；风浪联合概率模型；概率方法；设计波浪要素；台风环境

0　引言

海上结构物主要受风、海浪等可变作用力作用。规范[1]中涉及风、浪的计算时，当有较长期波浪实测资料时，可选出某一累积频率波高的年最大值系列进行频率分析，确定不同重现期的设计波高；当无较长期测波资料时，则根据当地的风速资料间接确定不同重现期的设计波浪。第1种方法虽然能够得到较准确的设计波高，但是未明确风影响因素，无法从设计角度加以考虑;第2种方法以风速的重现期为波浪的重现期，与事实不尽相符。有研究[2]根据风速和有效波高同步观测资料，用Gumbel逻辑模型来拟合风速和有效波高的联合分布，在有风、浪同步数据的情况下不失为一种好方法，但未将海浪周期纳入研究。

本文研究建立在某大桥所在地海洋站(下文简称海洋站)2001—2003年的海浪短期观测资料基础上，将海面波动、风都作为随机过程考虑。为方便研究，还作了以下的简化和假设：

(1)对象海域处于同一天气形势下，风场的宏观结构相同；

(2)海域足够大，不考虑近岸影响；

(3)水深足够大，忽略水深对海浪的影响；

(4)海浪考虑综合效应，不分风浪、涌浪，忽略波群；

(5)忽略考虑海(潮)流的影响。

本文在一些已有研究的基础上，取长补短，将台风环境下海上结构主要承受作用的关键要素风速、浪高和浪周期结合起来进行概率分析，推导出相应的概率分布模型，据此计算出基于台风环境的设计波浪要素，即使在缺乏长期观测数据的情况下，也能为海上结构设计提供可参考的设计参数。

1　短期测波资料频率分析

(1)

(2)

对该海洋站的实测波高特征值H1/10进行分级统计[6]，采用截尾正态分布[7]对该波高累积频率点进行拟合，其拟合分布模型为：

(3)

式中参数μH1/10，σH1/10由极大似然估计法算出。截尾正态分布函数的估计值有如下表达式：

(4)

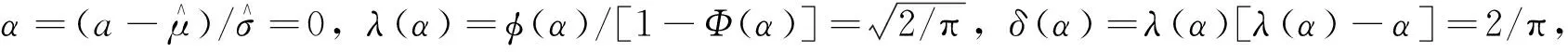
波高累积频率点及其截尾正态分布拟合曲线如图1所示，图中横坐标为波高h,纵坐标为波高h的累积分布函数，无量纲。

图1　波高拟合分布曲线Fig.1　Fitting distribution curve of wave height

同理，对同期波浪周期特征值T1/10进行分级统计，采用对数正态分布进行拟合，其拟合分布模型为：

(5)

式中μT1/10，σT1/10同上由极大似然估计法算出。波浪周期累积频率点及其对数正态分布拟合曲线如图2所示，图中横坐标为波浪周期t,纵坐标为周期t的累积分布函数，无量纲。

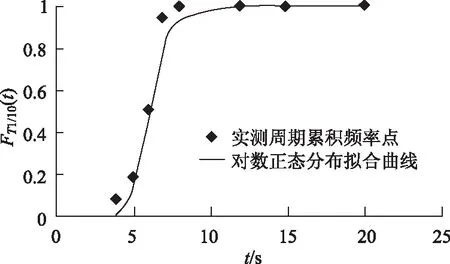
图2　周期拟合分布曲线Fig.2　Fitting distribution curve of wave period

采用Kolmogorov-Smirnov法对以上拟合进行检验，计算结果表明：在显著性水平α=0.05时波高分布能通过假设检验；在显著性水平α=0.01时周期分布能通过假设检验。

2　给定风速条件下的设计波高、周期

2.1风速分布模型

风速概率分布模型采用应用得最为广泛的双参数Weibull分布，其累积分布函数形式如下：

(6)

式中，k为形状参数；λ为尺度参数。在缺乏该地同期风观测实时记录的情况下，需借助一些间接方法估算k，λ。

假设各年风速观测值独立同分布，其累积分布函数FV(v)与风速年极值累积分布函数FVmax(v)当FV(v)→1时，存在以下关系：FV(v)≈[FVmax(v)]1/N，N为N年。根据海洋站1976—2005年30 a风速年极值所得桥址处的基本风速，按式(6)计算可得桥址处风速观测值(地面或水面以上10 m高度处10 min平均风速)累积分布函数值FV(v)如表1所示。

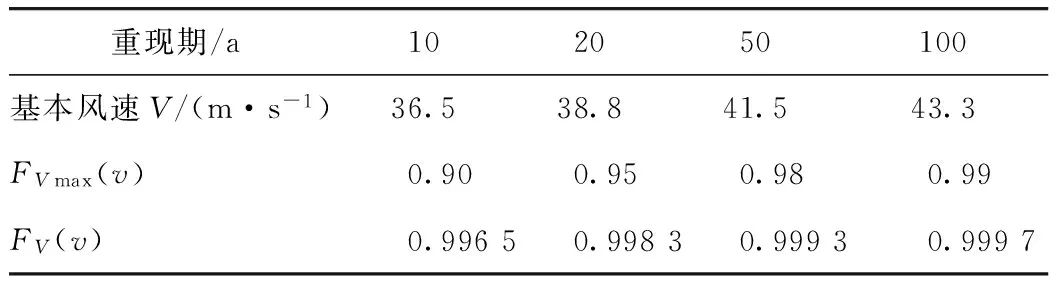
表1　桥址处基本风速

选用表1中FV(v)更趋于1的后两组数值(v,FV(v))代入式(6)，即可得k=2.15，λ=16.46风速累积分布曲线见图3，图中横坐标为风速V，纵坐标为风速V的累积分布函数，无量纲。

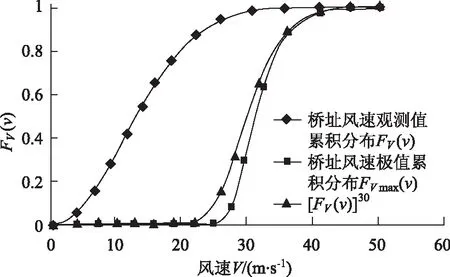
图3　风速分布曲线Fig.3　Distribution curve of wind velocity

若视风速V大于某一阈值v0的事件为泊松过程，则在时间间隔[t0,t0+τ]内n次出现事件A={V≥v0}的概率为：

(7)

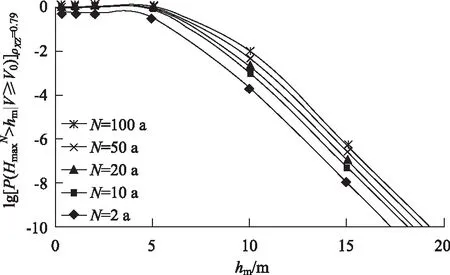
式中，κ为强度，代表单位时间内事件A出现的平均次数。一年内事件A一次未发生可表示为{N(t0+1)-N(t0)=0}，对风速则可表示为{年极值Vmax

(8)

当v0为12级台风风速32.7 m/s时，κ=0.422y-1。

2.2风速条件V≥v0下的波高、周期联合概率分布

根据Nataf变换原理[8-9]，波高、波周期、风速标准正态化见式(9)：

(9)

并认为波高X与风速Z相关，有ρXZ，认为波周期Y与风速Z不相关，即ρYZ=0。由式(9)可得一定风速条件V≥v0下的波高、周期联合概率密度函数[3]：

(10)

当ρXZ=0时，即波高、风速不相关，fH1/10,T1/10|V≥v0(h,t|V≥v0)=fH1/10,T1/10(h,t)，(H1/10,T1/10)分布不受风速的影响。假设波高、周期相关系数ρXY=0.6，风速阈值v0取12级台风风速32.7 m/s，波高、风速相关系数ρXZ分别取0，0.4，0.7，0.79，得台风时波高、周期等概率密度曲线随参数ρXZ变化的趋势如图4所示，图中横坐标为波高h，纵坐标为周期t。可知，随着ρXZ变大，fH1/10,T1/10|V≥v0(h,t|V≥v0)等概率曲线右移，形状趋于狭细，即波高愈大，周期愈集中，但因为指定ρXY、“斜率”(波高、周期相关性)不变，周期稍有增大但变化不大。

以上推导过程主要参考文献[3]。

图4　fH1/10,T1/10|V≥v0(h,t|V≥v0)等概率曲线随ρXZ变化趋势Fig.4　Probability curves of fH1/10,T1/10|V≥v0(h,t|V≥v0) varying with ρXZ

2.3风速条件V≥v0下的最大波高分布

2.3.1时间τ内的最大波高分布

同一波系n个波高中的最大波高Hmax满足极值Ⅰ型分布，累积分布函数[4]为：

(11)

当n很大时，exp(-n) ≈0，在时间段τ内，n=τ/t，t为周期，深水条件下H=H1/10/2.031，则累积分布可变换为：

(12)

则可得风速条件V≥v0下，最大波高Hmax的条件超值概率函数为：

fH1/10,T1/10(h,t|V≥v0)dtdh,

(13)

式中,时间段τ=min{τwave,τwind}，其中τwave为波系历时，τwind为风速条件V≥v0持续时间。参考有关文献[9-10]，τwave=2 h，τwind=4 h，…，则有τ=2 h。如果ρXY=0.6，v0=32.7 m/s，ρXZ=0.0，0.2，0.4，0.6，0.79，为便于观察结果作lg[P(Hmax>hm|V≥v0)]τ=2 h曲线如图5所示，图中横坐标为波高hm,纵坐标为波高hm的超值概率函数的常用对数，无量纲。可知，最大波高hm越大，超值概率P(Hmax>hm|V≥v0)越小；ρXZ越大，超值概率P(Hmax>hm|V≥v0)越大。

图5　台风持续时间内最大波高Hmax随ρXZ变化的超值概率曲线Fig.5　Overflow probability curves of maximal wave height Hmax varying with ρXZ during a typhoon event

2.3.2N年最大波高分布

风速条件V≥v0下的最大波高{Hmax(t)|V≥v0,0≤t≤T}可作为滤过复合Poisson过程,如图6所示。图中横坐标为时间t,纵坐标为最大波高Hmax考虑表示为：

(14)

式中，{N(t),t∈[0,T]}为一以κ为强度的Poisson过程，其值由式(8)确定；ξn(n=1,2,…。)为第n个出现的风速条件最大波高值，它们是独立同分布于FHmax|V≥v0(hm|V≥v0)的随机变量序列，且与N(t)独立，并令ξ0=0。

(15)

式中，τn(n=1,2,…。)为第n个出现的风速条件最大波高所持续的时间。记Tn(n=1,2,…。)为ξn-1出现到ξn出现所需的时间，且τn≪Tn，并令τ0=0。

图6　滤过复合Poisson过程样本函数示意图Fig.6　Schematic diagram of sample function of filtered composite Poisson process

(16)

式中，台风时的κ=0.422y-1。如果ρXY=0.6，ρXZ=0.79，分别取N=2，10，20，50，100，作lg[P(HmaxN>hm|V≥v0)]曲线如图7所示，图中坐标涵义如图5所示。易知，同一ρXZ，N越大，超值概率P(HmaxN>hm|V≥v0)越大。

图7　台风下ρXZ=0.79的N年最大波高HmaxN随N变化的超值概率曲线Fig.7　Overflow probability curves of maximal wave height HmaxN during N years under typhoon event varying with N (ρXZ=0.79)

2.4设计波浪要素

为了计算给定风速条件下与特征波高对应的波浪周期，可推导出周期在一定波高条件下的条件概率密度函数见式(17)：

(17)

如果ρXY=0.6，v0=32.7 m/s，ρXZ=0.0，0.2，0.4，0.6，0.79，计算台风下与每一波高H1/10相对应的周期众值(T1/10)mode。如图8所示，图中横坐标为波高H1/10，纵坐标为周期众值(T1/10)mode。可知，周期随波高呈单调递增趋势，ρXZ越大，周期增势越快。与规范[1]推算方法相比，曲线斜率相差不大，本文方法所求周期值偏小。

图8　台风下H-Tmode随ρXZ变化曲线Fig.8　Curves of H-Tmode under typhoon event varying with ρXZ

对于设计特征波的波高，规范[1]规定，强度设计应采用H1%；中国1982年和1983年分别制定的《海上移动式钻井船入级与建造规范》[12]和《海上固定平台入级与建造规范》[13]规定，设计波高采用最大波高的众值(Hmax)mode。本文针对台风环境这一极端情况进行研究，如果按常规取H1%难免偏于保守，因此，应着眼于最大波高Hmax。

本文以2001—2003年短期测波资料作为分析依据，其中包含该海洋站所在地经历的两次台风袭击，在台风资料匮乏的条件下，具有一定的代表性，更为重要的是，提出这样一种思路的分析方法。

3　结论

海上结构传统设计一般单独考虑风、海浪，得到一定重现期下的设计特征值，与实际情况不符。本文通过对短期测波资料进行概率分析，建立概率模型并作出拟合分布曲线。建立风速概率分布模型，从随机过程的角度求出台风下强度κ=0.422y-1。

表2　台风时不同ρXZ的设计波浪要素

[1]JTJ 213—98，海港水文规范[S].

JTJ 213—98,Code of Hydrology for Sea Harbour[S].

[2]周道成，段忠东．耿贝尔逻辑模型在极值风速和有效波高联合概率分布中的应用[J]．海洋工程，2003，21(2)：45-51.

ZHOU Dao-cheng,DUAN Zhong-dong.The Gumbel-logistic Model for Joint Probability Distribution of Extreme-value Wind Speeds and Effective Wave Heights[J].The Ocean Engineering,2003,21(2):45-51.

[3]DITLEVSEN O.Stochastic Model for Joint Wave and Wind Loads on Offshore Structures[J].Structural Safety,2002,24(2002):139-163.

[4]邱大洪．波浪理论及其在工程中的应用[M]．北京：高等教育出版社，1985：155，158-170.

QIU Da-hong.Wave Theory and Its Application in Engineering[M].Beijing:Higher Education Press,1985:155,158-170.

[5]竺艳蓉．海洋工程波浪力学[M]．天津：天津大学出版社，1991：184-185.ZHU Yan-rong.Ocean Engineering Wave Mechanics[M].Tianjin:Tianjin University Press,1991:184-185.

[6]李远林．波浪理论及波浪载荷[M]．广州：华南理工大学出版社，1994：255-257.

LI Yuan-lin.Wave Theory and Wave Loads[M].Guangzhou:South China University of Technology Press,1994:255-257.

[7]COHEN A C.Estimating the Mean and Variance of Normal Populations from Singly Truncated and Doubly Truncated Samples[J].Annals of Mathematical Statistics,1950,21(4):557-569.

[8]DER KIUREGHIAN A,LIU P L.Structural Reliability under Incomplete Probability Information[J].Journal of Engineering Mechanics,1986,112(1):85-104.

[9]LIU P L,DER KIUREGHIAN A.Multivariate Distribution Models with Prescribed Marginals and Covariances[J].Probabilistic Engineering Mechanics,1986,1(2):105-112.

[10]GHOSN M,MOSES F.Design of Highway Bridges for Extreme Events[R].Washington,D.C.:Transportation Research Board,2003.

[11]李扬海．公路桥梁结构可靠度与概率极限状态设计[M]．北京：人民交通出版社，1997.

LI Yang-hai.Highway Bridge Reliability and Probabilistic Limit State Design[M].Beijing:China Communications Press,1997.

[12]中华人民共和国船舶检验局．海上移动式钻井船入级与建造规范[S]．北京：人民交通出版社，1982.

Register of Shipping of PRC.Rules for the Classification and Construction of Mobile Offshore Drilling Units[S].Beijing:China Communications Press,1982.

[13]中华人民共和国船舶检验局．海上固定式平台入级与建造规范[S]．北京：人民交通出版社，1983.

Register of Shipping of PRC.Rules for the Classification and Construction of Fixed Offshore Platforms[S].Beijing:China Communications Press,1983.

A Joint Probabilistic Model of Design Wave and Wind Parameters for Offshore Structures under Typhoon Circumstances

CHEN Yi-qian1,2,CHEN Ai-rong1,MA Ru-jin1

(1.School of Civil Engineering,Tongji University,Shanghai 200092,China;2.China Merchants Chongqing Communications Technology Research &Design Institute,Co.,Ltd.,Chongqing 400067,China)

In order to study the main extreme actions on offshore structures,based on the data of some short term wave observation,combining wave height and wave period with wind speed,which has an important influence on the formation and development of ocean wave,the joint probabilistic model of wave height and wave period under the given wind velocity condition is derived,and the parameter analysis is performed on the correlated coefficients of wave height and wind speed.Regarding the maximal wave height duringNyears under the given wind velocity condition as a filtered composite Poisson process,its cumulative distribution is derived,from which the mode of annual maximal wave height and the corresponding characteristic period in typhoon circumstance for a given return period are inverted to obtain the design characteristic wave height and period in typhoon circumstance.The result shows that the corresponding relationship between the wind and wave design factors is established by the derived model from the aspect of probability,which simplified the calculation of traditional design parameters.

bridge engineering;joint probabilistic model of wave and wind;probability method;designed wave parameter;typhoon circumstance

2015-01-20

国家科技支撑计划项目(2014BAB16B05)

陈忆前(1980-)，女，重庆人，博士研究生.(yiqianch@126.com )

10.3969/j.issn.1002-0268.2016.01.014

U441+.2

A

1002-0268(2016)01-0089-06