硼氮富勒烯图环4-边割的刻画

蒋晓艳



硼氮富勒烯图环4-边割的刻画

蒋晓艳

（惠州学院 数学系，广东 惠州 516007）

硼氮富勒烯图是连通、正则的平面图，且每个面要么是四边形，要么是六边形. 本文刻画了有非平凡环边割的硼氮富勒烯图，即有非平凡环边割，则是一类管状图，或的一个分支是2个相邻的四边形，或的一个分支是3个相邻的四边形（即第1个与第2个相邻，第2个与第3个相邻，但第1个与第3个不相邻）.

硼氮富勒烯图；环边连通度；环边割

1 引言及预备知识

图1 示意图

2 有非平凡环4-边割的硼氮富勒烯图的刻画

文献[10]计算了硼氮富勒烯图的环边连通度，结果如下.

定理1[10]109对硼氮富勒烯图，若，则的环边连通度为3，否则为4.

由定理1知，硼氮富勒烯图环边连通度为3的图只有一类管状图，所以下面只需讨论环边连通度为4的图的非平凡环边割.

a.示意图 b.帽子 c.示意图

关于硼氮富勒烯图的面圈有以下结论：

引理1[11]1892设是硼氮富勒烯图的一个长圈，则是一个面圈的边界.

引理2[11]1892设为硼氮富勒烯图. 若是的一个长圈，则是

1）一个六角形面的边界，或

2）2个相邻四边形面的边界，或

3）有一个公共点的3个相邻四边形面的边界.

下面给出本文的主要结论.

图3 示意图

另一方面，根据点、边、面的关系可以得到：

a.有4个相继度点 b.有3个相继度点 c.有3个相继度点

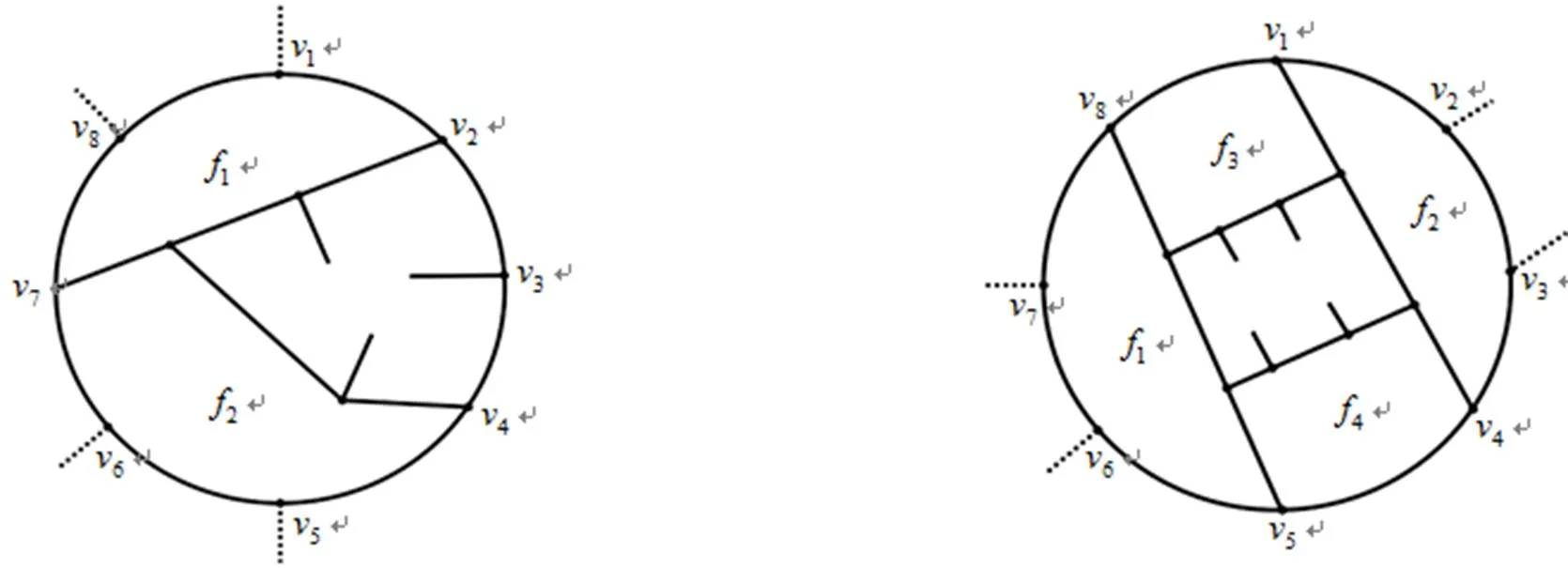
a.有2个相邻度点,和,b.有2个相邻度点,和,

c.有2个相邻度点, d.有2个相邻度点,

图6 子情况3.4示意图

综合以上分析，我们可得到定理2的结论.

[1] FOWLER P, HELNE T, MITCHELL D, et al. Boron-nitrogen analogues of fullerenes: the isolated-square rule [J]. J Chem Soc Faraday Trans, 1996, 92(12): 2197-2201.

[2] LIN Chengde, TANG Peng. Kekule count in capped zigzag B-N nanotubes [J]. J Chem Inf Comput Sci, 2004, 44: 13-20.

[3] SHIU W C, LAM P C B, ZHANG Heping. Clar and sextet polynomials of buckminster-Fullerene [J]. J Mol Struct (Theochem), 2003, 622: 239-248.

[4] STROUT D. Fullerene-like cages versus alternant cages: isomer stability of B13N13, B14N14 and B16N16 [J]. Chem Phys Lett, 2004, 383: 95-98.

[5] ZHU Hongyao, KLEIN D, SEITZ W, et al. B-N alternants: boron nitride cages and polymers [J]. Inorg Chem, 1995, 34: 1377-1383.

[6] KOCHOL M. A cyclically 6-edge-connected snark of order 118 [J]. Discrete Math, 1996, 161: 297-300.

[7] LOU Dingjun, HOLTON D A. Lower bound of cyclic edge connectivity for-extendability of regular graphs [J]. Discrete Math, 1993, 112: 139-150.

[8] NEDELA R, SKOVIERA M. Atoms of cyclic connectivity in cubic graphs [J]. Math Slovaca, 1995, 45: 481-499.

[9] KUTNAR K, MARUSIC D. On cyclic edge-connectivity of fullerenes [J]. Discrete Appl Math, 2008, 156: 1661-1669.

[10] DOSLIC T. Cyclical edge-connectivity of fullerene graphs and (,6)-cages [J]. J Math Chem, 2003, 33: 103-111.

[11] JIANG Xiaoyan, ZHANG Heping. On forcing matching number of boron-nitrogen fullerene graphs [J]. Discrete Appl Math, 2001, 159: 1581-1593.

[责任编辑：熊玉涛]

Characterization of Cyclic 4-edge Cut of Boron-nitrogen Fullerene Graphs

JIANGXiao-yan

(Department of Mathematics, Huizhou University, Huizhou 516007, China)

A boron-nitrogen fullerene graph is a 3-connected, 3-regular planar graph, and each face is square or hexagon. In this paper, we characterize boron-nitrogen fullerene graphwith non-trivial cyclical-4-edge cut, that is,has non-trivial cyclical-4-edge cut, thenis a type of tubulous graph, or a component ofis two adjacent squares, or a component ofis three adjacent squares (the first is adjacent to the second square, the second is adjacent the third square, but the first is not adjacent to the third square.)

boron-nitrogen fullerene graph; cyclical-edge connectivity; cyclical-edge cut

1006-7302（2016）02-0009-05

O157.5

A

2015-12-24

广东省普通高校青年创新人才项目（2015KQNCX152）；惠州学院博士启动基金（C5110208）

蒋晓艳（1982—），女，山东青岛人，讲师，博士，研究方向为应用数学.