复杂截面螺杆数控铣床包络法加工研究

谭伟强，杨铁牛



复杂截面螺杆数控铣床包络法加工研究

谭伟强，杨铁牛

（五邑大学 机电工程学院，广东 江门 529020）

针对成形法在加工一些变螺距、变深度、变螺棱等复杂的螺杆时存在加工精度低、加工效率不高的缺陷，提出了复杂截面螺杆的包络加工方法. 文章从数控包络原理出发推导出了变深变螺距螺旋面方程，并将此方程编入数控程序当中，通过加工实例论证其可行性. 结果表明：在加工参数相同的条件下，原来的铣床加工的螺旋槽至少需要，运用包络法原理加工需要，且加工精度明显高于前者.

包络法；螺杆加工；数控铣床；空间螺旋面

作为注塑挤出工艺的核心部件，螺杆的加工精度将直接影响注塑产品的质量，而螺杆形状的多样性和复杂性决定了它的加工难度. 注塑行业一般用成形法在改进的机械式专用螺杆机床上加工螺杆，但由于不同规格的螺旋面需要相应的配套刀具和刃磨设备，导致企业生产成本投入大、加工效率低. 文献[1-2]分别介绍了铣切法、刀具变速移动法、改造数控车床法、分段加工法、分层加工法等以获得理想的变螺距螺杆，这些方法在一定程度上提高了变螺距螺杆的加工精度，但对于一些更为复杂的螺杆截面和空间曲面，其加工精度低、加工效率不高的缺陷仍旧存在. 对于变螺棱、变螺距、变深度等复杂廓形螺杆的数控铣床加工，本文提出包络加工法. 与成形法加工相比，包络法加工具有很多优点，如加工时多轴联动，控制精度和加工效率高；可采用标准刀具，刀具成本低、磨损易更换；适用于多种规格的螺杆加工，运用范围广. 由于双铣头数控铣床具有2个独立运动的大拖板，本研究在其上安装两把铣刀（均含圆头铣刀、圆锥铣刀、圆柱铣刀等3种刀型），以对不同段的螺距包络加工，并以此提高加工效率[3].

1 数控铣床包络加工概述

在进行包络法数学建模前，需明确工件和刀具的运动关系. 以图1双铣头数控螺杆铣床结构示意图为例，铣刀在电机带动下绕轴线旋转为轴，伺服电机通过主轴箱带动丝杠传动完成大拖板的轴向运动为轴，小托板位于大拖板上通过电机带动小丝杠完成铣刀的径向进给运动为轴，工件绕主轴（轴）旋转为轴.

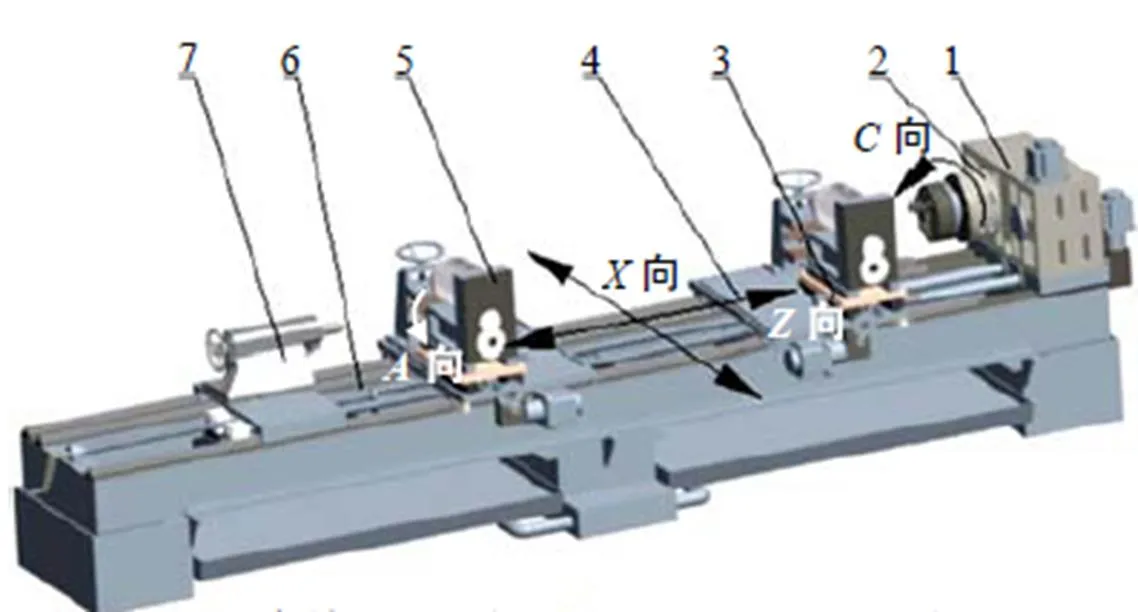
1.主轴箱；2.卡盘；3.小托板；4.大拖板；5.铣刀支座；6.主传动丝杠；7.尾座

为了描述刀具和工件间的运动包络状态，需建立工件坐标系和刀具坐标系间的关系. 数控机床坐标轴的名称及运动方向ISO有统一的规定，具体见文献[4]. 如图2所示，工件坐标系固定在工件端面上，规定工件轴线为轴，与刀具轴线平行的为轴，根据笛卡尔右手法则可确定轴的方向，绕工件轴线旋转为轴. 刀具坐标系固定在刀具端面上，为了减少运算，可设刀具坐标轴与工件对应坐标轴平行，绕刀具轴线旋转为轴. 由两坐标系相应轴平行可得到刀具坐标和工件坐标间的转换公式：

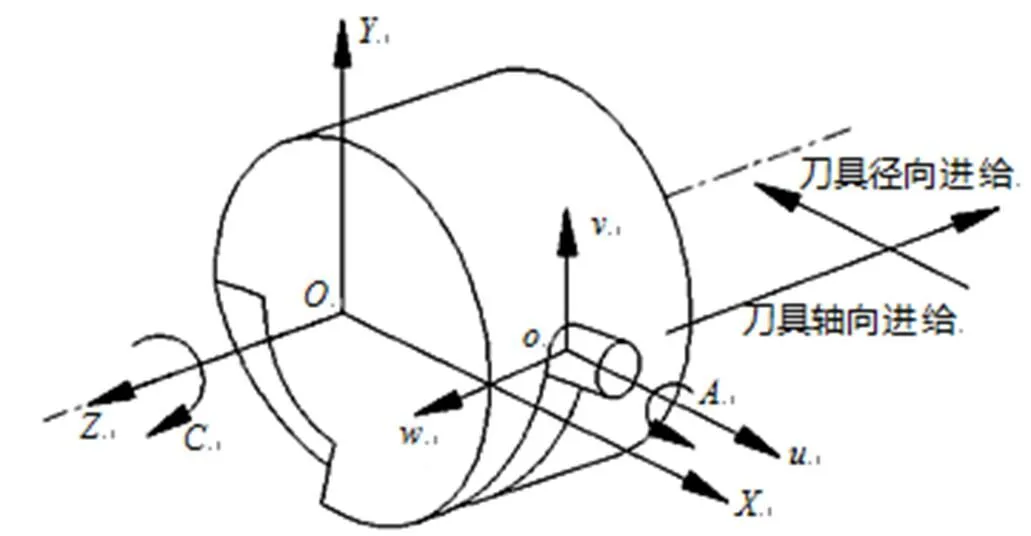
图2 刀具坐标系和工件坐标系

2 螺杆包络螺旋面方程的建立

根据铣床包络原理可知，工件包络螺旋面的形成既与刀具的运动状态有关，又与螺杆的几何形状有关. 由于刀具运动引起切屑点的变化，而切屑点又与刀具的廓形有关，因此要建立包络螺旋面方程需清楚刀具的廓形方程；而不同的螺杆几何形状（等深变深、恒螺距变螺距）也将影响包络面的形成，所以建立包络螺旋面方程也需考虑螺杆的几何参数.

2.1 刀具模型的简化及刀具廓形方程的建立

为使刀具扫描体的计算不局限于某种特殊形状，考虑到刀具的旋转速度比进给速度大很多，若不计退屑需要采取的实际刀刃的螺旋形状，刀具体可以用一系列相连的直线或曲线的回转面来表示，其模型参见文献[5].

刀具切削工件时首先是刀具圆弧刀刃与工件接触，此时的接触点即切削点，随着刀具的转动，当前接触点移出，下一接触点进入. 因此，刀具模型可简化为将同一截面的系列接触点连接起来的轮廓，此时的接触线既是刀具廓形又是螺棱轴向截面的边界. 根据螺杆螺棱的截面形状，包络加工可选择3种刀型：初次切削螺旋槽时，可选用圆柱形铣刀包络加工（可切削大量金属），直至接近槽宽（优点是加工效率高、刀具易更换）；当槽宽接近设计值时，换用圆锥铣刀或圆锥圆头铣刀来修正螺纹形状. 圆锥铣刀可包络加工凹螺旋面，当螺棱截面有一定角度时，可选择圆锥圆头铣刀包络加工圆角.3种简化刀形及其加工螺棱轴截面的形状如图3所示.

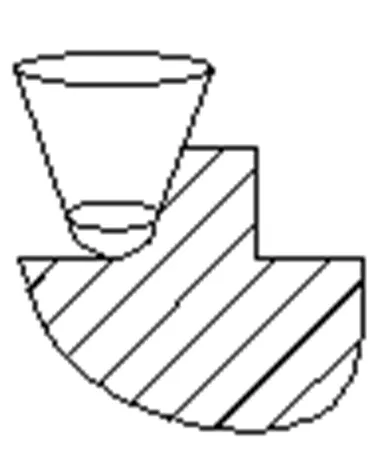
a.圆锥圆头铣刀 b.圆锥铣刀 c.圆柱铣刀

刀具进行包络加工时，接触线在刀具回转面和工件螺旋面的公切面上，若它沿轴向做空间螺旋运动即可得到包络面，此时加工出来的即为螺旋面，刀具回转面模型如图4所示.

a. 圆柱铣刀 b. 圆锥铣刀 c. 圆锥圆头铣刀

根据刀具回转面模型，求出刀具坐标系下的刀具廓形方程. 以较复杂的圆锥圆头铣刀廓形为例，为刀具半径，为切屑刃高，为圆锥半角，在平面内设半圆圆心坐标为，则刀刃廓形圆弧方程为：，；其直线方程为：

由式（1）、式（2）得到圆锥圆头铣刀的廓形方程如下：

类似地可以得到圆柱铣刀、圆锥铣刀的廓形方程，这里不详述.

2.2 工件螺旋面方程的建立

螺杆螺槽容积由左右螺旋面和底部轮廓组成的包容空间构成. 实际加工时，三把刀具主要完成容积主体切削，形成螺旋槽，故工件螺旋面可以看作是它的端截面、轴向、偏轴截面或法截面的截形作螺旋运动而形成的[6]. 本文以轴截面截形的右旋螺旋面为例进行论述.

a.工件坐标系b.轴截面 c.端截面

图5 工件坐标系及截形

将式（6）展开，得到：

用直角坐标系可表示为：

根据等差数列有以下关系：

由式（11）可推导出：

代入式（8）得：

2.3 包络螺旋面方程

综合刀具廓形方程、工件螺旋面方程和螺距等差数列规律，可得到基于铣刀廓形所形成的空间螺旋面方程. 下面以圆锥铣刀廓形为例，其切削深度为、棒料直径为，刀具坐标系原点在工件坐标系下为，则工件坐标系下铣刀廓形方程为：

数控系统采用位置控制模式，反映到方程里面就是运动参数角位移，加工变螺距时通过主轴的旋转角度来控制轴的联动，、、、、均为螺杆的几何参数，式（15）是根据刀具廓形方程推导出的螺旋面方程. 若、值不变，当加工变深螺杆时，深度发生变化意味着螺旋面宽度变化，刀具原点坐标向垂直于工件轴线方向运动，沿工件轴向方向上的运动不影响空间螺旋面的形成，此时，，为螺杆深度变化量，其为0时即为等深螺杆加工，为初始切削深度，为当前主轴转过的角度值，为加工段变深时主轴需要转过的相对角度.

3 加工论证

某公司研发的高效数控螺杆铣床采用LABVIEW语言编程，将式（15）用LABVIEW编入数控程序的数据中心，以此控制铣床三坐标轴的运动. 实验螺杆材料为尼龙，长度，直径，数控系统程序面板输入螺杆参数，螺距值从变到，总加工长度，螺距深度，主轴转速. 在螺杆加工参数和主轴转速同样的条件下，测得用一般方法加工长的螺杆耗时，用数控包络法加工耗时，对于长的普通螺杆，就加工螺旋槽而言，至少节省了半个小时的加工时间，明显提高了加工效率，同时测得包络法加工的螺杆螺距值误差，也符合要求.

图7 螺杆加工实例

4 结束语

本文通过对数控铣床包络原理的分析和刀具模型的简化，从刀具廓形和螺杆轴截面入手，推导出了刀具廓形方程和螺杆螺旋面方程，阐述了数控加工下包络法的数学模型和匀加速下变螺距的形成机理，这为包络法数值仿真和数控程序编写提供了重要的借鉴. 当然，对于包络法加工还需要更深入的研究，本文提及的铣刀仅沿轴向径向和绕自身轴线运动，而包络运动是三轴的合成运动，对于更多自由度运动的铣刀，其包络运动则更为复杂.

[1] 白宇，王平. 变螺距螺杆的加工方法[J]. 现代制造工程，2008(1): 24-26.

[2] 李富荣. 等牙顶宽变螺距螺杆的数控4轴加工[J]. Cad/cam与制造业信息化，2014(3): 79-82.

[3] 黄李辉. 双铣头螺杆数控系统的研发[D]. 江门：五邑大学，2013.

[4] 全国工业自动化系统和集成标准化技术委员会. 数字控制机床坐标和运动方向的命名JB3051—1999 [S]. 北京：机械科学研究院，1999.

[5] 周春雷. 包络法加工复杂曲面中刀具通用几何模型的研究[J]. 机电工程技术，2010, 39(10): 80-81.

[6] 吴序堂. 齿轮啮合原理[M]. 北京：机械工业出版社，1980.

[7] 陈永广. 基于IPC的螺杆双铣刀专用数控系统的研发[D]. 江门：五邑大学，2010.

[责任编辑：熊玉涛]

A Study of the Enveloping Machining of CNC Milling Machines for Screws of Complex Section

TANWei-qiang, YANGTie-niu

(School of Mechanical and Electrical Engineering, Wuyi University, Jiangmen 529020, China)

Because the traditional forming method has the defects of low machining accuracy and low machining efficiency in the processing of complex screws with variable pitches, variable bottom diameters, variable spiral angles, the enveloping machining technology is put forward. Based on the principle of numerical control enveloping, this paper derives the equation of variable pitches and variable bottom diameters, and the equation is used in numerical control programs and the feasibility of the method is demonstrated through machining examples. The results show that: under the same conditions, when thespiral groove is processed by the conventional milling machine, it takes at least; when enveloping method is adopted, it takes, and the machining accuracy is obviously higher than that of the former.

the envelope method; screw machining; CNC milling machines; spatial spiral surfaces

1006-7302（2016）02-0055-06

TG547

A

2015-09-17

谭伟强（1989—），男，湖南株洲人，在读硕士生，主要从事机械设计制造的研究；杨铁牛，教授，博士，硕士生导师，通信作者，主要从事机械设计制造、IC装备压力分布等研究.