高速永磁同步电机转子瞬态温度场解析解

贾修建，孙岩桦，程文杰，刘中华，虞 烈



高速永磁同步电机转子瞬态温度场解析解

贾修建1，孙岩桦1，程文杰2，刘中华1，虞 烈1

（1. 西安交通大学机械结构强度与振动国家重点实验室，西安710049；2. 西安科技大学理学院，西安710054）

在转子的热设计中，很自然地有如下要求：在已知转子内热源的条件下，确定转子需要多大的对流换热系数以及相应气隙流体温度，使得转子局部最高温度不超过设计值。内热源已知的条件下，实验测量转子温度和气隙流体温度便可得到相应的对流换热系数。为解决高速永磁电机转子热设计问题，本文给出了转子温度场的解析解。首先将时变的且含内热源的传热方程无量纲化，然后利用傅里叶积分变换法求解，其中轴向分布不均的对流换热系数和气隙流体温度用等效的对流换热系数和等效气隙流体温度代替。通过与有限元计算结果对比，验证了该解析解的正确性。获得了一类高速永磁电机转子在各种散热因素作用下的稳态最高温度分布图，为转子的热设计提供了理论支持。

永磁同步电机；转子；温度场；热设计

0 前言

目前，常用的稀土钴或者钕铁硼永磁体的剩磁和矫顽力均随温度的上升而降低。过高的温度会使永磁体励磁磁通减小（引起电机偏离设计工作点），甚至造成永磁体永久性退磁（电机失效）。不可否认，高速将带来诸多优点，如整机尺寸减小、结构紧凑、重量减轻。但是，如果转子没有经过合理的热设计，这些优点反而会加强转子散热的困境。于是，永磁体转子的热设计非常重要。

转子热设计的最终目标是采用合适的冷却方式将整根转子的温度控制在设计范围内。其中冷却方式对转子散热的影响可以用对流换热系数来描述；转子温度的上升来自于其内部的内热源，即电机的损耗（涡流损耗和空气摩擦损耗等）。高速永磁电机的设计过程涵盖多个学科，如电磁学、转子动力学、流体力学、传热学等。为此，需要构建估算转子温度场的解析解，以便于综合其他物理场来评判转子设计的合理性。

由于转子本身含有内热源，转子温度场的预测可以归结到求解瞬态的含内热源的传热方程。特别地，当永磁体为圆筒形或者圆柱形时，采用解析解求解温度场成为可能。虽然对于几何形状及边界条件都比较简单的问题可以获得解析解[1]，但是求解特殊几何结构和边界条件下的解析解仍然充满着挑战。M.H.Kayhani[2]在2009年采用分离变量法求解了无内热源，纤维绕制圆筒在平面内的稳态温度场解析解，其中纤维具有正交各向异性的导热属性。针对具有一般边界条件（传导、对流和辐射的线性组合）的这种纤维圆筒，2012年该作者在文献[3]中求解了其在平面内的稳态温度场解析解，其中利用Sturm-Lionville定理推导了合适的傅里叶变换。对于多层圆筒（径向方向套接）的二维瞬态温度场，当圆筒端面为绝热时的解析解已被较早地研究过，如文献[4]采用分离变量法求解了单层和双层气缸的温度场。当圆筒端面为恒温时，或者一端恒温，一端绝热时，X.Lu[5]采用一种新颖的分离变量法获得了其瞬态温度场解析解。同时X.Lu[6]将这种新颖的分离变量法与Laplace变换结合起来求解了多层圆盘（轴向叠加）的瞬态温度场，其中圆盘上下表面（轴向）为对流换热边界条件，侧面为恒温边界条件。当处理含有内热源的瞬态传热方程时，目前有两种方法可以借鉴：有限积分变换法和基于分离变量法的“拆分法”。文献[7-8]利用双重有限积分变换法求解了含内热源的轴向叠加的圆筒和径向套装的多层圆筒的瞬态温度场。对于前者，在轴向上采用Fourier积分变换，在径向上采用Hankel积分变换；对于后者，在径向上采用Hankel积分变换，在周向上采用Fourier积分变换。另外一种求解含内热源的径向套装多层圆筒瞬态温度场解析解的技巧是：在周向上将物理量（温度场，边界条件等）展开成傅里叶级数，然后在径向上进行一次积分变换，最后进行反变换，如文献[9]所处理的那样。基于分离变量法的“拆分法”的处理技巧是[10]：将含内热源的瞬态传热方程拆分成不含内热源的瞬态传热方程与含内热源的稳态传热方程（边界条件相应改变），用分离变量法求得这两个方程的解之后，再叠加即得到原问题的解。

虽然采用有限元法可以求取永磁转子温度场，但是它缺少解析解那样的洞察力，而且移植性也不好，即解析解能和其他的解析解（比如电磁场和应力场等）一起进行双向耦合分析，尤其方便于优化设计，但是目前鲜有关于永磁体转子温度场解析解的文献报道。本文首先将描述转子温度场的控制方程—含内热源的瞬态传热方程无量纲化，然后采用有限积分变换法求解，以获得三层永磁转子温度场解析解。

1 基本假设及其物理模型

高速永磁同步电机转子结构如图1所示，其中环形永磁体沿直径切成两半后扣在心轴上，然后外面热套一个圆筒，即保护套。

图1 永磁转子实际结构

作如下假设：

（1）不考虑转子轴向上的温度分布，即对流换热系数和气隙流体的温度都用沿轴向的平均值代替。

（2）转子属性，比如比热容、密度、热导率等不随温度变化；事实上，永磁转子的工作温度一般不超过250℃，转子材料属性在此温度之内变化很小。

（3）转子材料的传热属性是各向同性的，并且各层材料之间接触良好。

于是转子的物理模型可以用图2描述。

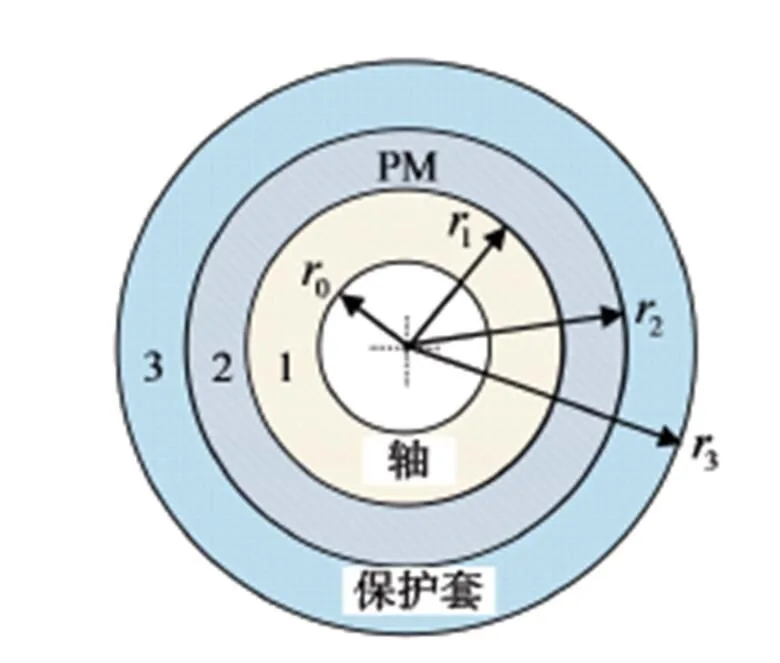
图2 永磁转子物理模型

2 控制方程及边界条件和初始条件

转子温度场的控制方程可以写成[7]：

AD9833可将DAC数据的最高有效位输出。通过对OPBITEN（D5）控制位置1，可将VOUT引脚输出DAC数据的最高有效位。这可以作为粗调时钟源。这个方波还可在输出之前进行2分频。控制寄存器的DIV2（D3）bit控制VOUT引脚提供的此输出的频率。

转子内表面换热边界条件为：

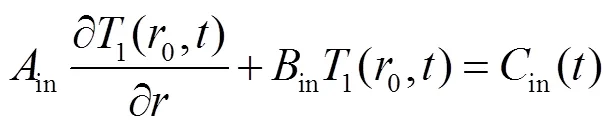
若心轴为实心，则式（2a）简化成：

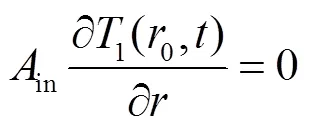
转子外表面换热边界条件为：

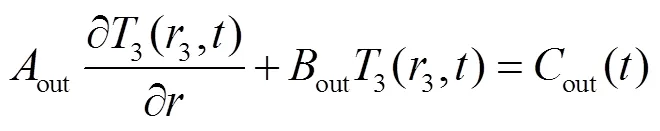
转子配合面的边界条件为：

（5）

式（4）和式（5）分别表明温度场和热流量在配合面处连续。

初始条件为：

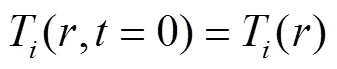
3 方程及边界、初始条件的无量纲化

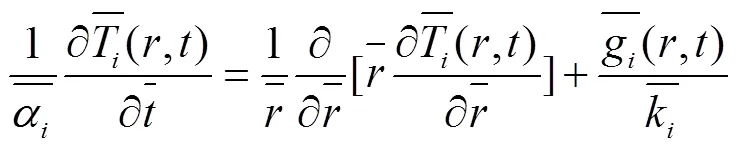
式（2a）和式（2b）相应地变成：

（8b）

式（3）变为：

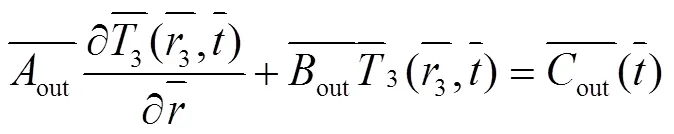
式（4）~（6）分别变为：

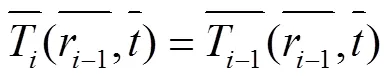
（11）

4 多层转子瞬态温度场解析解

为表述方便，特将无量纲量的上划线标记省略，如不特殊说明，以下各量均为无量纲时的情形。为求解式（7），将其两边乘上，并在上积分得到：

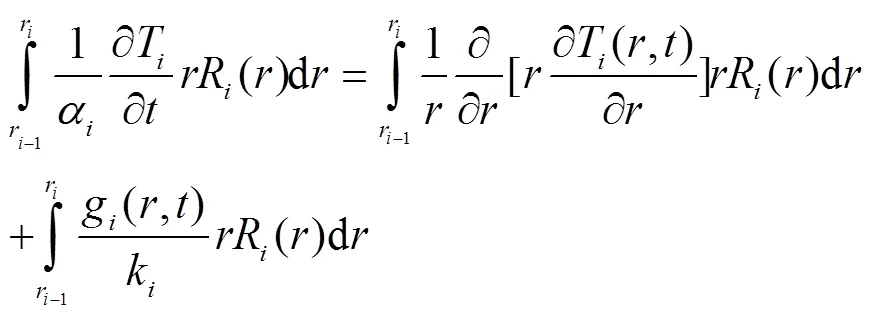
并且对于第一层转子部件有：

对第三层转子部件有：

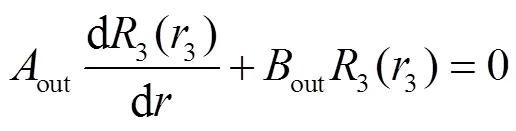
在转子配合面有：

（18）

将式（19）带入式（15）~（18），得到如下方程组

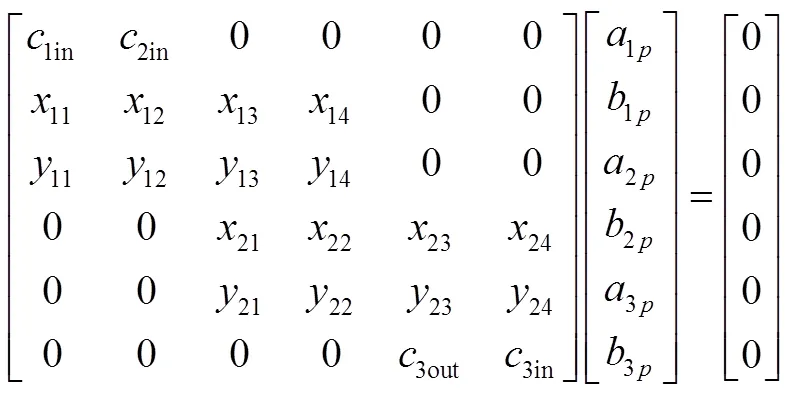
其中各系数的表达式如下：

三个特征根满足如下关系[9]：

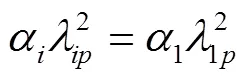
将式（22）代入到式（21）中，可以得到只含有一个未知量的系数矩阵。若要式（21）有非零解，系数矩阵行列式必须为零。所以根据这一关系，可解出。

将式（19）代入到式（17）和（18）得到：

由式（21）第一行展开得到：

将式（14）代入到（13）得到：

将式（22）带入到式（25），然后将式（25）两边同时乘上，并对取和，得：

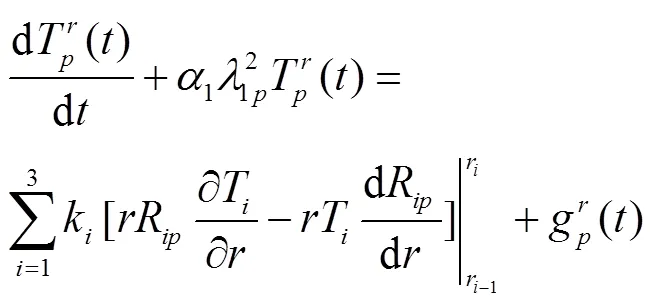
利用边界条件，式（26）右端第一项可以化成：

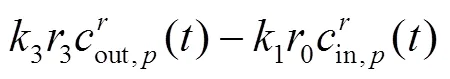
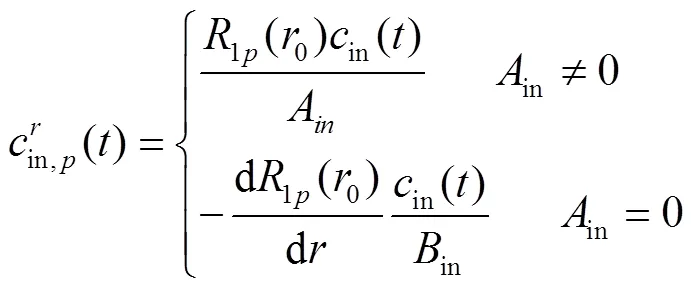
于是式（26）可以写成：

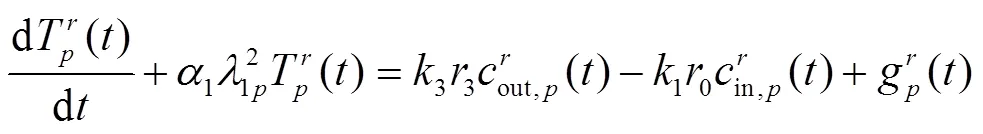
式（30）的解为：

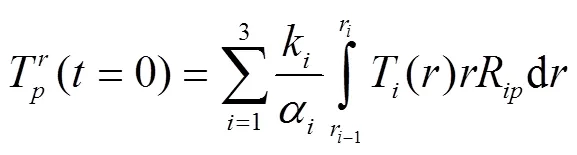
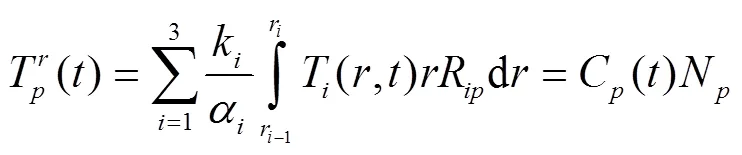
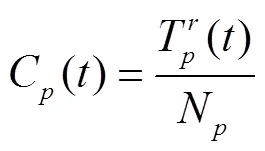
将式（34）代入式（33）得到：

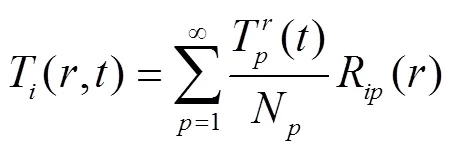
式（35）便是原问题的解析解。

5 算例

表1 转子的材料属性

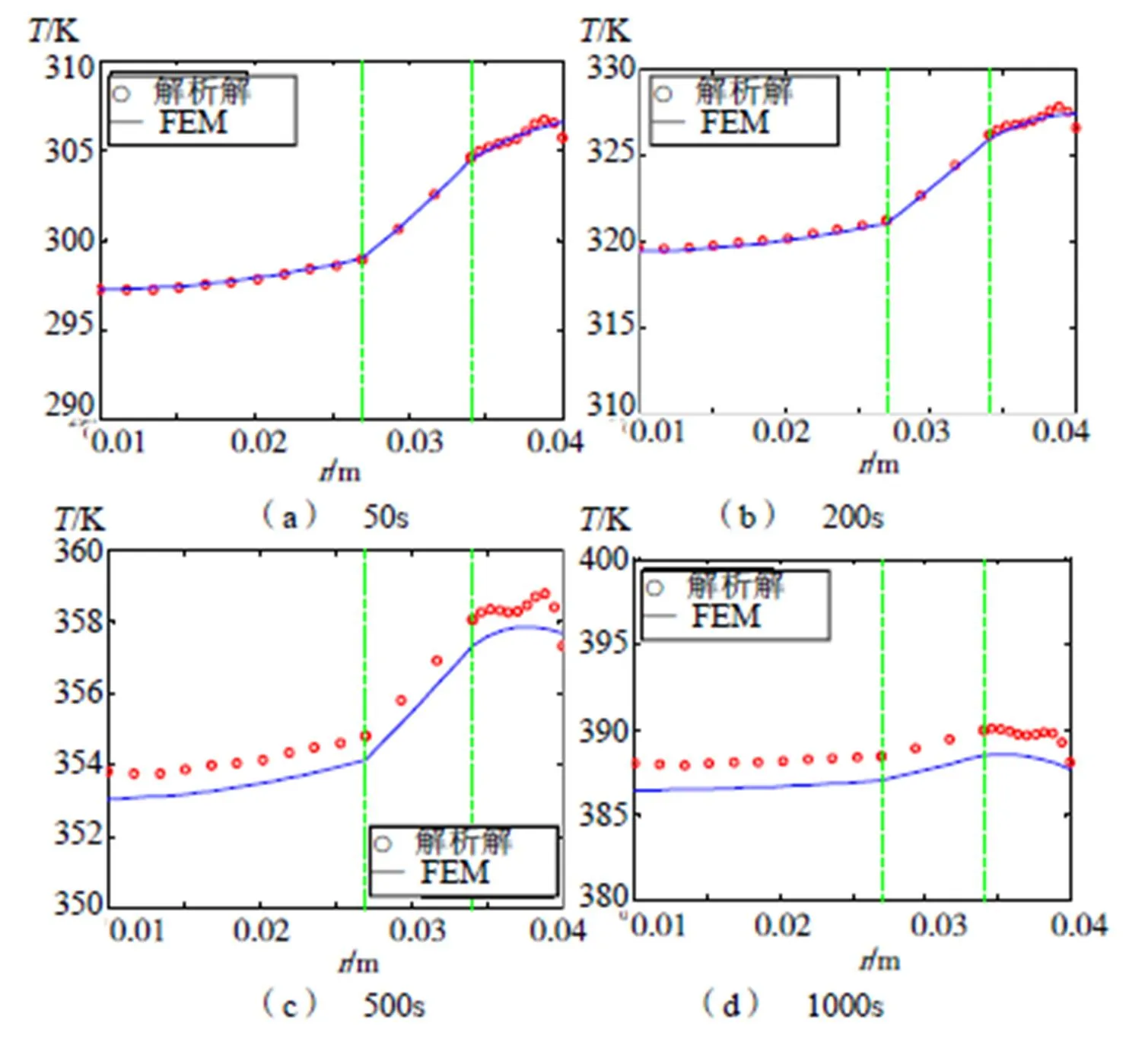
图3 不同时刻转子温度场的解析解与有限元结果对比

从图3可见，解析解和有限元解吻合非常好，验证了解析解的正确性。在50s时，保护套的温度最高306K，心轴温度最低297K，温度由外径向内径方向逐渐降低，温差为9K。200s时，温度分布趋势不变，保护套的温度为327.5K，永磁体温度为320K，径向方向温差为7.5K。500s时，该温度趋势仍然不变，保护套的温度为359K，永磁体温度为354K，径向方向温差为5K。1000s时，保护套的温度为390K，永磁体温度为356.5K，径向方向温差为3.5K。这说明转子内温度场随着时间逐渐趋于均匀。

6 内热源密度以及冷却条件对转子温度的影响

转子的温度场由以下因素决定：热源密度、对流换热系数以及气隙流体的温度。其中，内热源密度由反映。当转子采用外表面强迫空气冷却时（定转子间隙的轴向流），对流换热系数由反映，气隙流体温度由反映。对以上三个因素分析，可以获得一类转子的稳态最高温度分布图。通过它能够方便地估算出这类转子的稳态最高温度，或者反过来估算出对流换热系数。本节引入无量纲量进行永磁转子的散热规律研究。仍以算例5中的转子为研究对象，进行无量纲化后，，，，，分别取3.675、1.837、1.225、0.918，分别取1.043、1.076、1.110、1.143，取0.062~30，计算结果如图4所示。

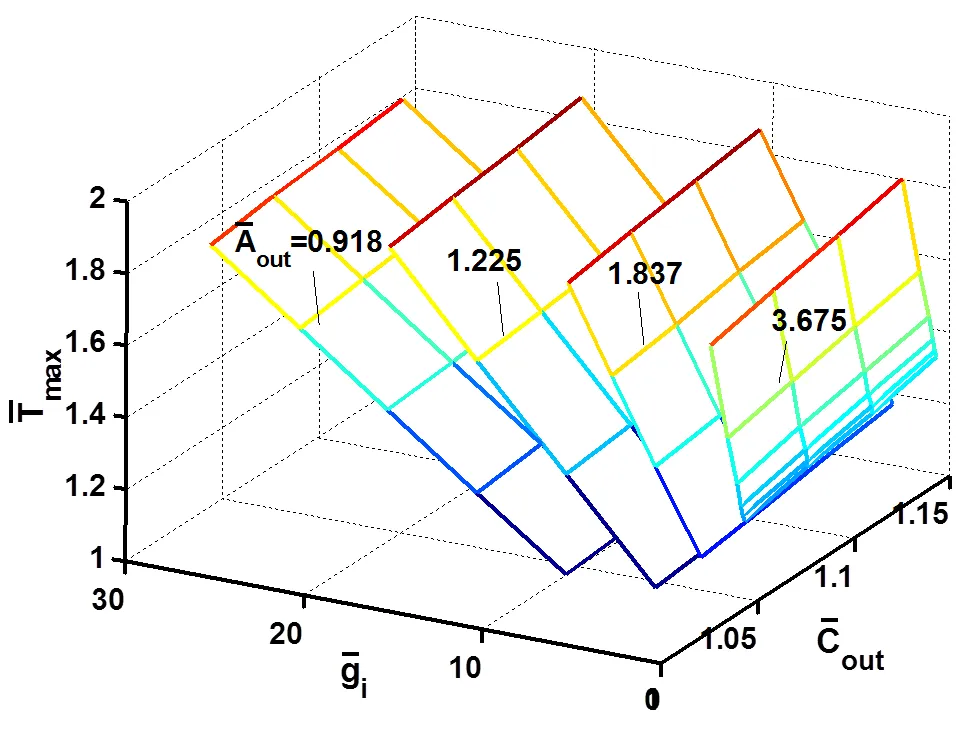
图4 各种因素对转子稳态最高温度的影响

7 结论

（1）本文采用有限积分变换法求解了含内热源的瞬态传热方程，获得三层（包含两层）永磁转子温度场解析解，并进行了有限元仿真。仿真与解析解结果对比证明了解析解的正确性。

（2）当气隙流体温度和内热源密度降低时，转子稳态最高温度线性降低。转子稳态最高温度主要由对流换热系数和内热源密度决定，气隙流体温度对转子散热的效果要比上述两个因素小，而且仅仅在对流换热系数较小时其影响较明显，对于较大对流换热系数情形，影响较微弱。

[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 71-71.

[2] M. H. Kayhani, M. Shariati, M. Nourozi. Exact solution of conductive heat transfer in cylindrical composite laminate[J]. Heat Mass Transfer, 2009, 46: 83-94.

[3] M. H. Kayhani, M. Nourozi, A. AmiriDelouei. A general analytical solution for heat conduction in cylindrical multilayer composite laminates[J]. International Journal of Thermal Sciences, 2012, 52: 73-82.

[4] 张学凯. 汽轮机气缸二维温度场理论研究[D]. 北京: 华北电力大学, 2008.

[5] X. Lu, P. Tervola, M. Viljanen. Transient analytical solution to heat conduction in composite circular cylinder[J]. International Journal of Heat and Mass Transfer, 2006, 49: 341-348.

[6] X. Lu, P.Tervola, M. Viljanen. Transient analytical solution to heat conduction in multi-dimensional composite cylinder slap[J]. International Journal of Heat and Mass Transfer, 2006, 49: 1107-1114.

[7] V. V. Mel'nikov. Nonstationary heat transfer in a hollow composite cylinder[J]. Journal of Applied Mechanics and Technical Physics, 2005, 46(2): 257-266.

[8] V. V. Mel’nikov. Unsteady heat transfer in a system of three coaxial finite cylinders[J]. Journal of Engineering Physics and Thermophysics, 2007, 80 (1): 148-158.

[9] Suneet Singh, PrashantK.Jain, Rizwan-uddin. Finite integral transform method to solve asymmetric heat conduction in a multilayer annulus with time-dependent boundary conditions[J]. Nuclear Engineering and Design, 2011, 241: 144-154.

[10] Suneet Singh, PrashantK.Jain, Rizwan-uddin. Analytical solution to transient heat conduction in polar coordinates with multiple layers in radial direction[J]. International Journal of Thermal Sciences, 2008, 47: 261-273.

[11] Wenjie Cheng, Haipeng Geng, Yanhua Sun, Lihua Yang and Lie Yu. Thermoanalysis of the permanent magnet rotor of the microturbine generator[J]. International Journal of Applied Electromagnetics and Mechanics, 2014, 45: 201-209.

An analytical solution to the transient temperature field in rotors of high speed permanent magnet synchronous motors

Jia Xiujian, Sun Yanhua, Cheng Wenjie, Liu Zhonghua, Yu Lie

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi'an Jiaotong University, Xi'an 710049, China; 2. Xi'an University of Science and Technology, Department of Basic Courses, Mechanics Research Center, Xi'an 710054, China）

In the thermal design of the rotor, the appropriate convective heat-transfer coefficient and temperature of the main flow need to be determined to guarantee its local temperature not exceeding the design value, whereas the corresponding convective heat-transfer coefficient can be ascertained through the experimental measured temperature of the rotor and main flow, when the heat sources are known. This paper proposes the analytical solution to the thermal field of the rotor for the thermal design of the high speed permanent magnet (PM) rotors. First, dimensionless formulation of the transient heat conduction equation including interior heat source is derived, where the axially uniform convective heat-transfer coefficient and main flow temperature are equivalent to their mean values. Next, the Fourier integral transform method is used to solve the dimensionless equation. Finally, the analytical solution is verified by simulation. According to the analytical solution, a distribution of stead maximum temperature of a class of high speed PM rotors can be obtained under different heat dissipations and provides a theoretical support in the thermal design of the rotor.

permanent magnet synchronous motors; rotor; temperature field; thermal design

TM351

A

1000-3983(2016)05-0001-06

2015-06-12

贾修建（1991-），西安交通大学机械工程学院硕士研究生，从事高速永磁电机耦合场研究。

国家自然科学基金资助项目(51175411，51139005，51275386，51375366)

审稿人：宫海龙