弹性支承块式轨道桥梁结构地震响应分析

韩　艳

(北方工业大学土木工程学院，北京　100141)



弹性支承块式轨道桥梁结构地震响应分析

韩艳

(北方工业大学土木工程学院，北京100141)

为研究弹性支承块式轨道结构对地震作用下桥梁结构位移、内力的影响，以某3跨预应力混凝土连续箱形高架轨道桥为例，利用Midas Civil软件建立考虑和不考虑具体轨道结构形式的高架轨道桥梁有限元模型，分析典型地震波作用下该高架桥梁的地震响应。结果表明：考虑具体轨道结构形式模型的连续梁桥主梁的位移、跨中正弯矩、支点负弯矩及支座处剪力均明显小于不考虑轨道结构形式模型的相应值，对主梁结构来说，设计中不考虑轨道结构形式是一种偏安全的设计方法，而考虑轨道结构模型的桥墩墩顶位移可能大于不考虑轨道结构形式模型的相应值，为安全起见，在进行轨道桥梁桥墩的抗震设计时应当考虑具体轨道结构形式的影响。

地震响应；弹性支承块式无砟轨道；有限元分析；轨道结构；桥墩

弹性支承块式无砟轨道结构(LVT)由于具有良好的弹性、减振降噪性能以及维修量少、总运营费明显小于有砟轨道等优点，自瑞士国营地铁首次采用以来便得到了较为广泛的应用。目前，我国很多轨道桥梁中也开始采用弹性支承块式无砟轨道结构[1]。对于这种轨道结构形式本身的动力特性以及与运行车辆的动力相互作用，我国学者已进行了较多的研究并取得了许多有用的研究成果[1-7]，而关于其对轨道桥梁的抗震性能的影响还缺乏系统的研究。到目前为止在城市轨道桥梁的抗震设计中，往往不考虑具体的轨道结构形式，只是将轨道结构的自重以恒载的形式施加在桥梁上。

城市高架轨道桥梁是现代化城市立体交通网络中关键的基础设施，其抗震性能的优劣直接关系到人民生命财产的安全和抗震救灾工作能否顺利进行。本文运用有限元软件Midas Civil对某一高架轨道连续梁桥分别建立了考虑和不考虑实际轨道结构形式的两种有限元模型，计算了在典型地震波作用下该高架桥的地震响应，并将2种模型的计算结果进行了对比分析，旨在探明弹性支承块式无砟轨道结构对桥梁抗震性能的影响，为合理地进行轨道桥梁的抗震设计提供参考。

1　考虑与不考虑具体轨道结构形式模型

1.1考虑与不考虑具体轨道结构形式计算模型

本文选取某典型的3跨预应力混凝土连续箱形高架轨道桥梁作为研究对象，分考虑具体的轨道结构形式与不考虑具体的轨道结构形式2种情况建立其抗震计算模型，二者均不考虑车辆对结构的影响。考虑轨道结构形式的高架桥模型中的轨道结构为弹性支承块式轨道结构，由钢轨及扣件、混凝土支承块、块下橡胶垫板、橡胶靴套、混凝土道床板及混凝土底座组成，如图1所示。

动力学仿真模拟时，不考虑具体轨道结构形式的模型中钢轨及轨道结构部分的重力视为二期荷载以均布荷载的形式直接作用在桥梁上；考虑具体轨道结构形式的模型中，钢轨、支承块、混凝土道床、底座均采用梁单元来模拟，钢轨、支承块之间的扣件、支承块和混凝土道床间的橡胶靴套和橡胶垫板视为均布的三向弹簧-阻尼器元件[8]。

1.2考虑与不考虑具体轨道结构形式模型参数

2种模型中的桥梁结构均为跨径33 m+54 m+33 m的预应力混凝土连续箱梁桥，双线轨道，桥宽9.2 m，箱梁桥的立面布置如图2所示，两中墩处的箱梁为3.2 m高的等截面形式，两边墩处的箱梁为1.8 m高的实腹等截面形式，从距中墩中心1 m至边墩中心8.9 m之间梁高按二次抛物线变化，在各跨的中间均设置0.2 m厚的横隔板。主梁典型的横断面尺寸见图3和表1。下部结构的构造示意如图4所示。

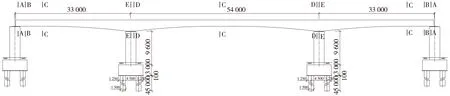
图2　桥梁立面(单位：mm)

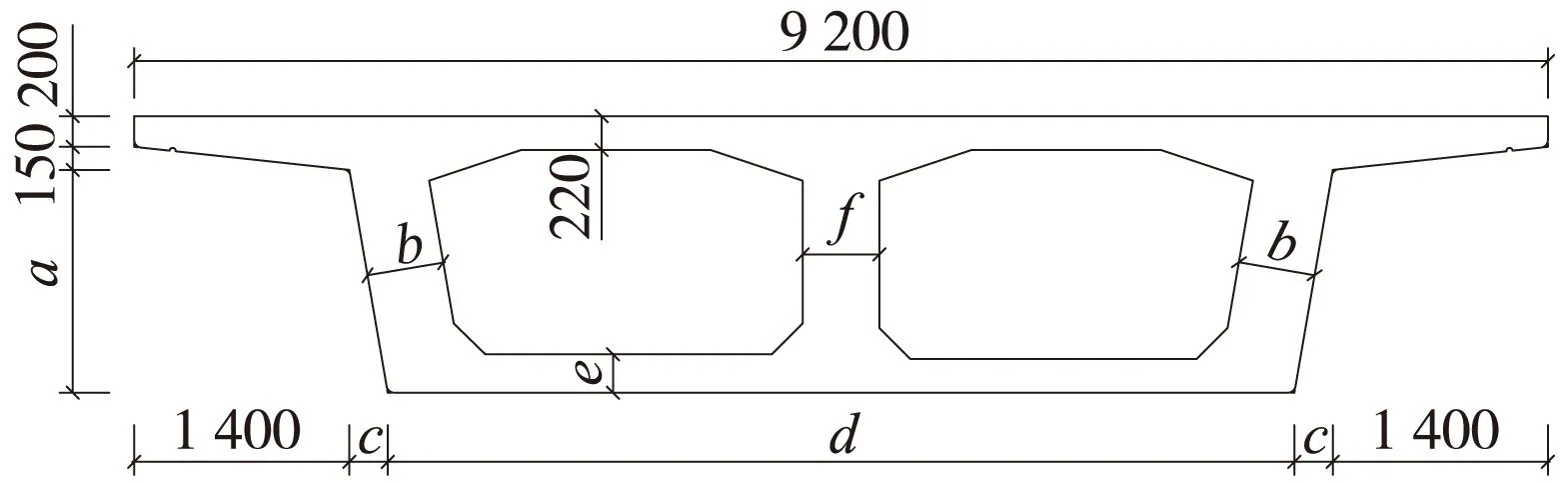
图3　主梁典型横断面示意(单位：mm)

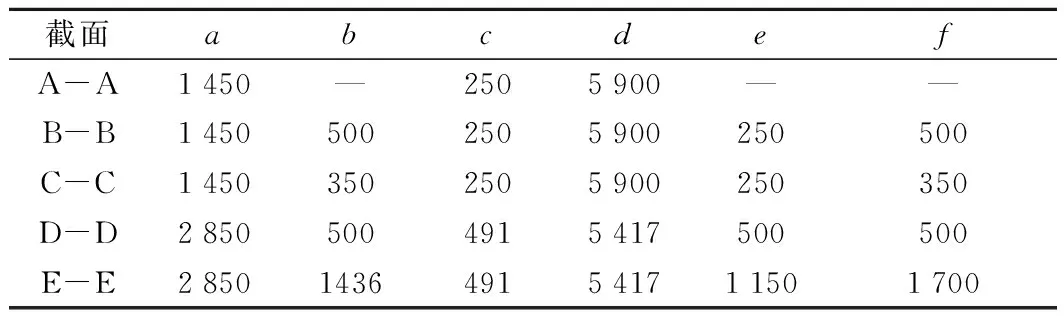
表1　主梁截面尺寸 mm

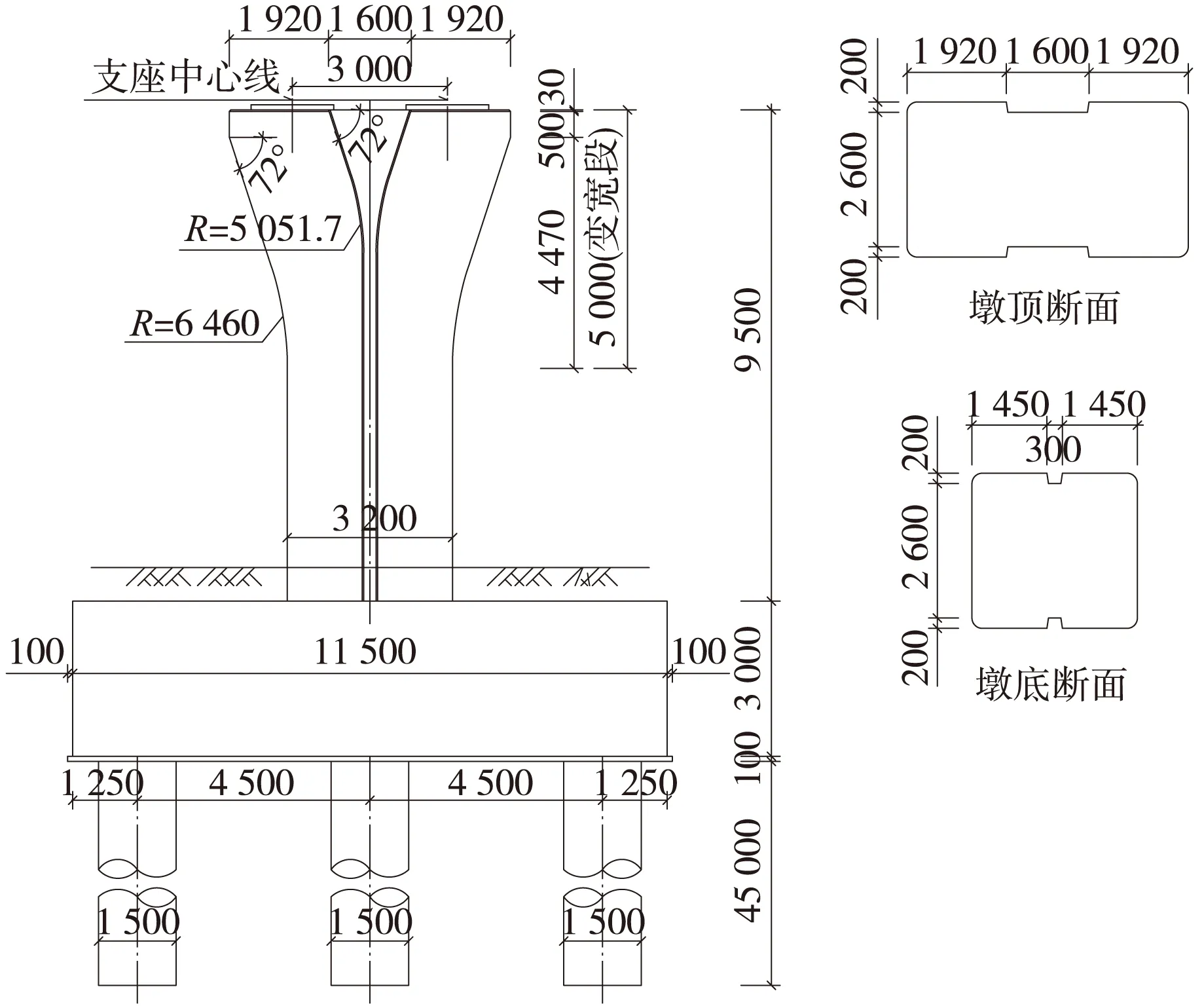
图4　桥墩构造示意(单位：mm)

为考虑相邻后继结构对桥梁抗震性能的影响，考虑与不考虑实际轨道结构形式的分析中均建立了两联的连续梁桥有限元模型，主梁、桥墩和桩基础均采用三维梁单元来描述，主梁与墩顶之间的支座采用一般连接中的滞后系统[9]来模拟，桩土之间的相互作用采用节点弹性支承以非线性土弹簧的形式模拟，非线性土弹簧采用理想弹塑性本构模型，其刚度按桥梁规范中的“m”法计算[10]，取m动=2.5m静。定义弹塑性材料特性时，钢筋采用二折线模型，混凝土采用Mander本构模型。桥墩的弹塑性铰定义为考虑轴力和2个方向上弯矩相互作用的P-M-M集中骨架铰形式[9]。

不考虑具体轨道结构形式的模型中，钢轨及轨道结构的自重视为二期荷载直接作用于桥梁上，其线荷载集度为104.9 kN/m。考虑具体轨道结构形式的模型中，建模时钢轨、支承块、混凝土道床、底座均采用梁单元来模拟，钢轨、支承块之间的扣件、支承块和混凝土道床间的橡胶靴套和橡胶垫板均视为均布的三向弹簧-阻尼器元件。桥上轨道结构采用弹性支承块式轨道系统，钢轨为60 kg/m重型无缝钢轨。根据文献[1，11-14]，本文的计算中轨道结构系统各部分的参数取值如表2所示。

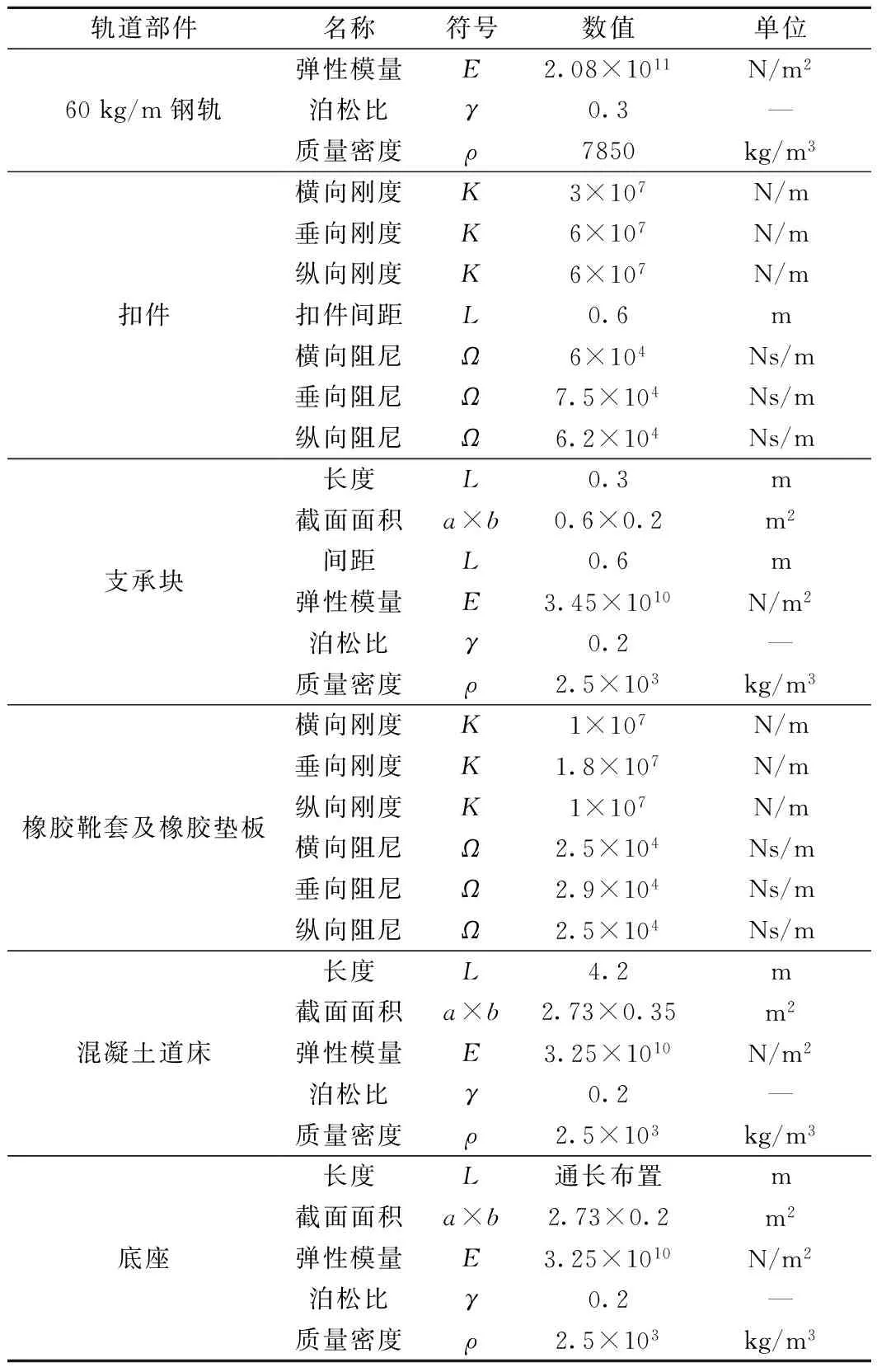
表2　考虑轨道结构形式模型计算参数

考虑轨道结构系统计算模型上部结构的侧视图和端视图分别示于图5和图6中，图中，Kpv、Kph、Cpv、Cph分别表示扣件的竖向刚度、横向刚度、竖向阻尼和横向阻尼，Kbv、Kbh、Cbv、Cbh分别表示橡胶靴套及垫板的竖向刚度、横向刚度、竖向阻尼和横向阻尼。在Midas civil中建立的考虑弹性支承块式轨道结构形式的有限元模型如图7所示。

图5　考虑轨道结构形式模型上部结构侧视示意

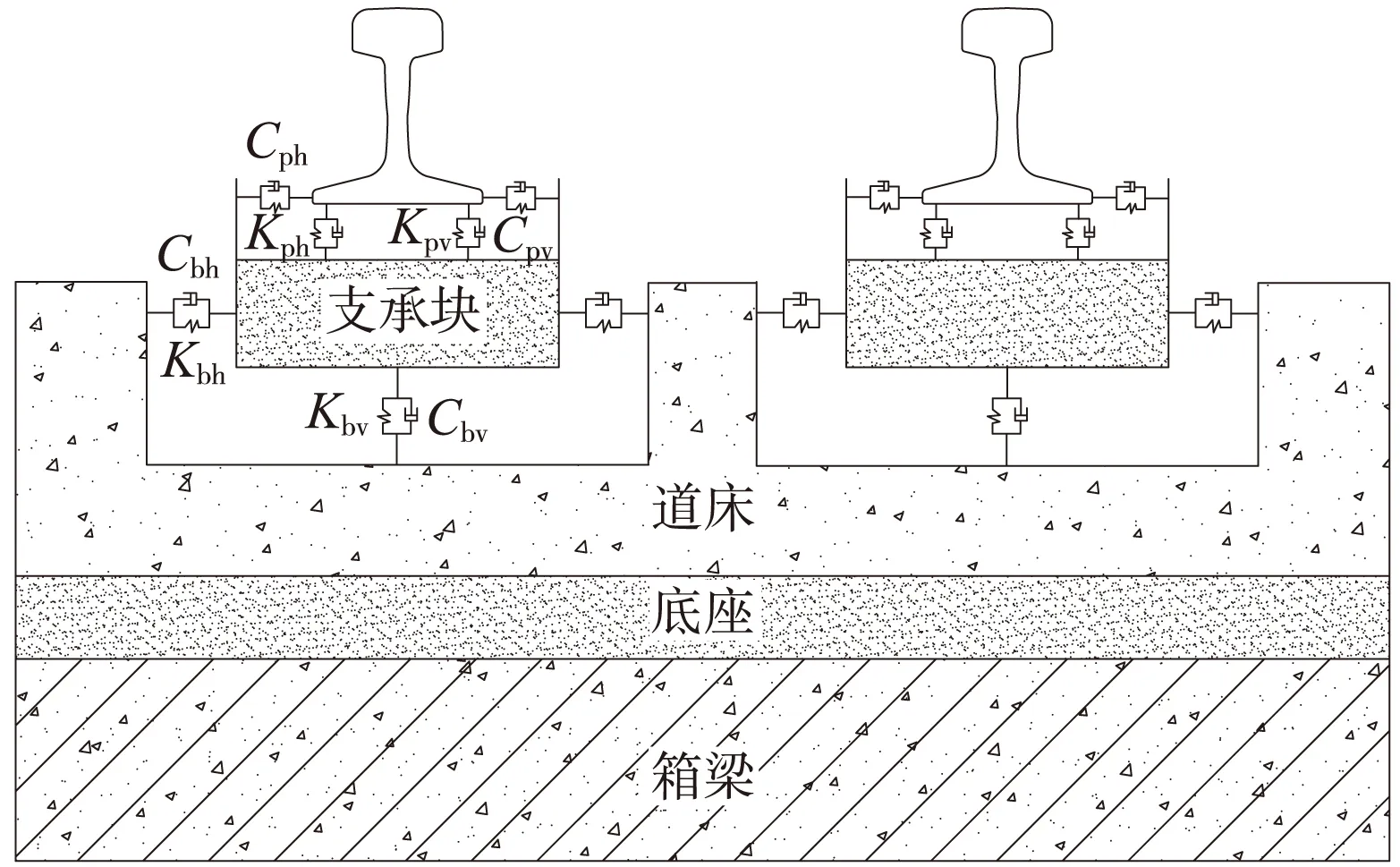
图6　考虑轨道结构形式模型上部结构端视示意

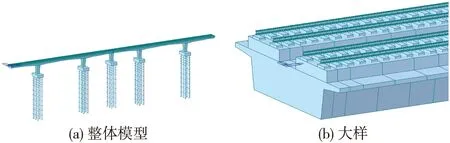
图7　考虑弹性支承块式轨道结构形式的有限元模型

2　高架轨道桥梁地震响应计算分析

2.1动力特性分析

桥梁结构的自振频率和振型是结构动力性能的综合反映，在Midas Civil软件中对考虑和不考虑具体轨道结构形式的桥梁模型采用多重Ritz向量法进行特征值分析，共考虑了90阶模态。不考虑具体轨道结构形式的桥梁模型顺桥向、横桥向和竖向的振型参与质量分别达到了99.77%、99.68%、99.98%，考虑具体轨道结构形式的桥梁模型顺桥向、横桥向和竖向的振型参与质量分别达到了99.91%、99.69%、99.99%，均满足文献[15]中大于90%的规定。动力特性分析中桥梁结构的前10阶自振周期及相应的振型列于表3中。

从表3可以看出，考虑具体轨道结构形式模型的自振周期均比不考虑具体轨道结构形式模型的自振周期小，这是由于考虑轨道结构形式的模型不仅计及了轨道的质量还计及了轨道的刚度，而不考虑轨道系统的模型只考虑了轨道的质量，忽略了轨道刚度的缘故。前10阶模态中，2种模型的第1、8～10阶模态完全相同，考虑轨道结构系统模型的第2、3、6阶模态分别与不考虑轨道结构系统模型的第5、6、7阶模态相同，这表明轨道结构形式对轨道桥梁的动力响应会有一定的影响，但影响不至于很大。

2.2输入地震加速度的确定

进行结构地震响应时程分析时，输入的地震加速度时程曲线要满足地震动三要素的要求，即频谱特性、有效峰值和持续时间要符合规定。本文所分析的轨道桥梁位于Ⅲ类场地土上。1940年El Centro地震波南北向的峰值加速度为0.357g，有效峰值加速度为0.295g，特征周期0.544 s，持续时间29.98 s；东西向的峰值加速度为0.214g，有效峰值加速度为0.200g，特征周期0.658 s，持续时间50.28 s；竖直方向的峰值加速度为0.247g，有效峰值加速度为0.122g，特征周期0.265 s，持续时间26.48 s，可以满足上述要求。按地震烈度7、8、9度的设计地震动将El Centro地震波进行调幅后，分别沿顺桥向、横桥向、竖桥向同时输入，并采用接续前次的非线性直接积分法分析。结构阻尼考虑为瑞利阻尼，选2个水平方向质量参与最大的振型计算质量因子与刚度因子，混凝土结构的阻尼比取为0.05。

在施加地震荷载前，将自重及二期荷载以动力(1 s内从无到有)的形式添加到结构上，采用非线性静力法计算其产生的效应。下文给出的结构地震响应均为已考虑了恒载作用后的计算结果。

2.3地震响应分析

图8和图9分别为地震动峰值加速度为0.2g时某桥墩墩顶和连续梁桥主梁中跨中的顺桥向和横桥向位移时程曲线。

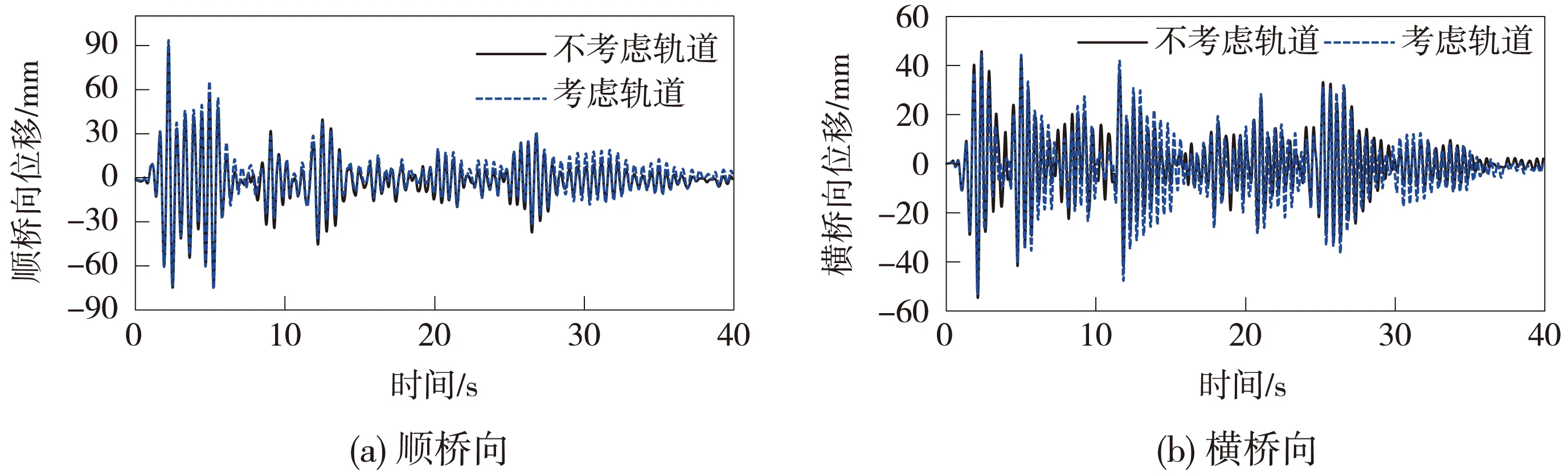
图8　地震动峰值加速度为0.2g时墩顶的位移时程曲线

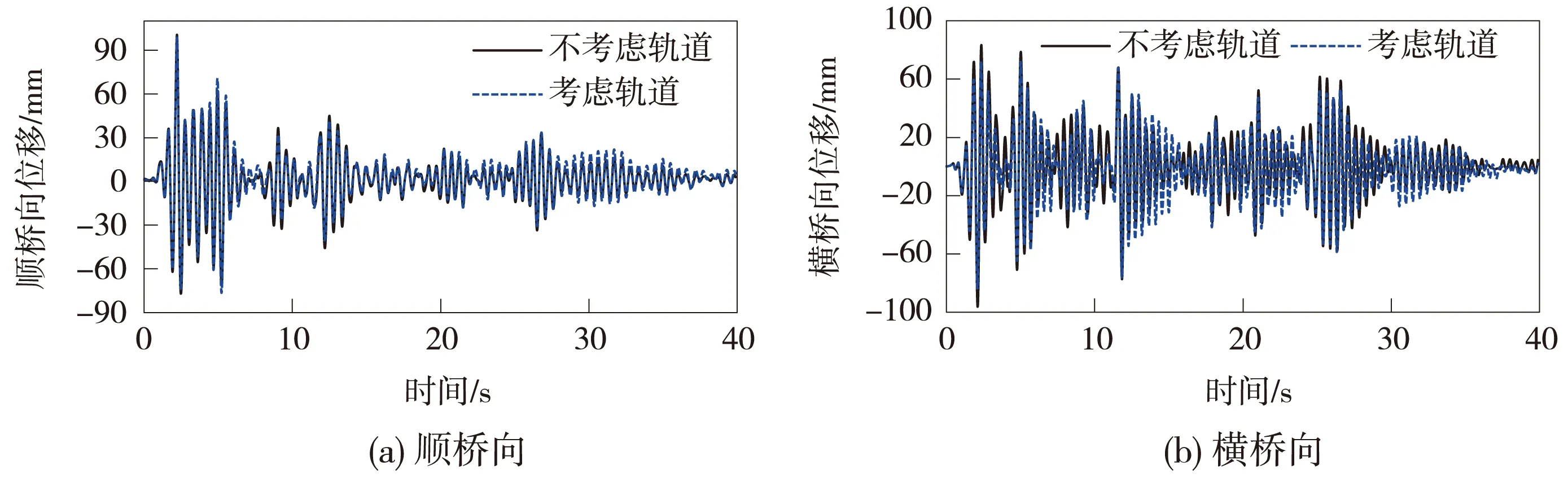
图9　地震动峰值加速度为0.2g时主梁跨中位移时程曲线

从图8、图9可以看出，在0.2g的地震动激励作用下，尽管在任一时刻考虑具体轨道结构形式的桥墩墩顶以及主梁跨中的顺桥向和横桥向振动位移值与不考虑具体轨道结构形式模型的相应值不尽相同，但按2种模型计算得到的相应位移随时间的变化规律基本一致。

表4给出了本文所考虑的高架轨道连续梁桥在不同地震动强度作用下，分别按考虑与不考虑具体轨道结构形式模型计算所得的连续梁桥主梁和桥墩墩顶位移响应的最大值。

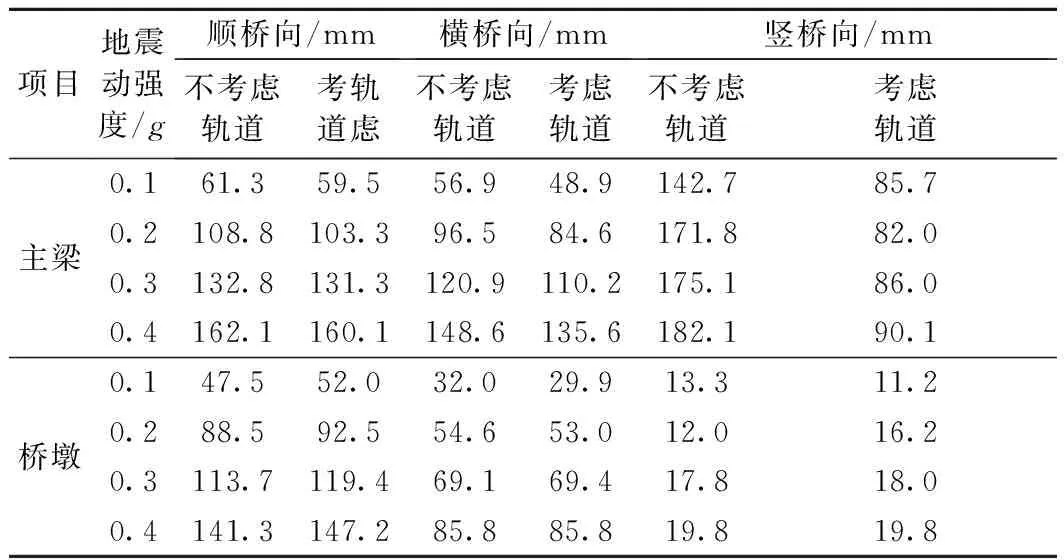
表4　不同地震强度作用下桥梁位移响应最大值

从表4中可以看出，在不同强度的地震动激励作用下，不考虑具体轨道结构形式模型的连续梁桥主梁位移最大值均大于考虑具体轨道结构形式模型的相应值，而不考虑具体轨道结构形式模型的桥墩顶顺桥向位移均小于考虑具体轨道结构形式模型的相应值，如在地震动峰值加速度为0.1g时，不考虑具体轨道结构形式模型所得的墩顶顺桥向位移为47.5 mm，考虑具体轨道结构形式模型所得的相应位移为52.0 mm，误差9.47%。桥墩是桥梁结构的主要承重构件，同时也是重要的抗侧力构件，在强地震动作用下允许其进入塑性工作阶段，桥墩墩顶位移的大小对桥梁结构整体倒塌起着举足轻重的作用，墩顶顺桥向位移过大，有导致落梁的危险。因此，在进行桥墩结构的抗震设计时，有必要考虑具体的轨道结构形式的影响。

图10和图11分别给出了考虑与不考虑具体轨道结构形式模型的高架轨道连续梁桥主梁结构支点负弯矩最大值、跨中正弯矩最大值和支点剪力最大值与地震动峰值加速度的关系曲线。

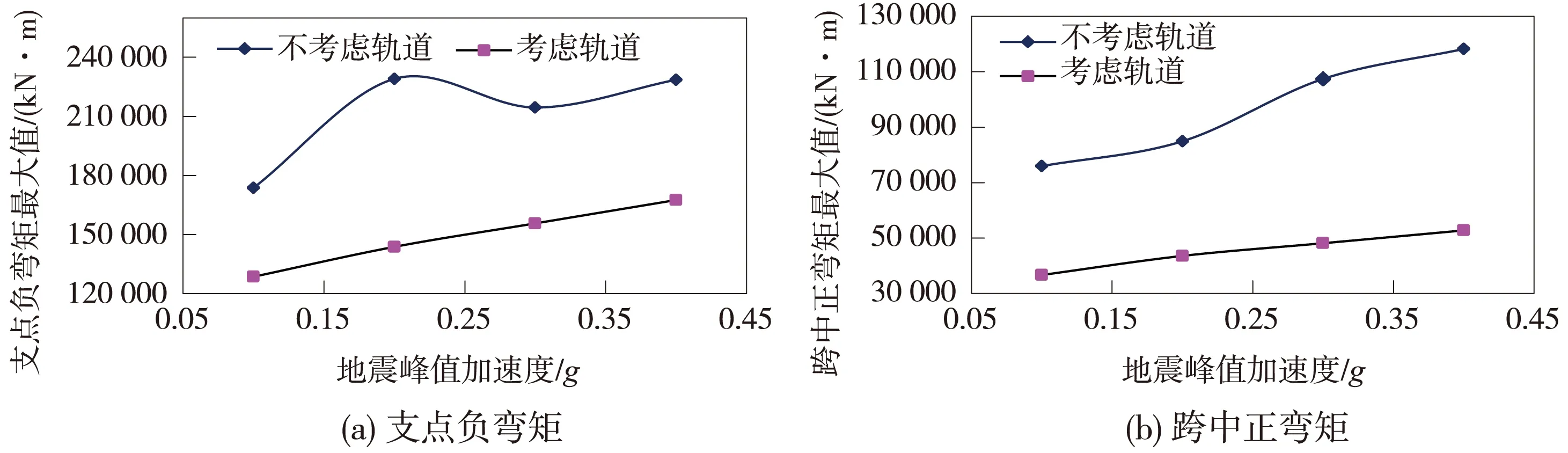
图10　桥梁弯矩最大值与地震峰值加速度关系

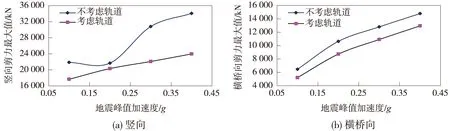
图11　支点剪力最大值与地震峰值加速度关系

从图10、图11可以看出，按2种模型计算所得的主梁内力最大值均具有随地震动强度增大而逐渐增大的趋势；在不同强度的地震动作用下，对于连续梁桥主梁结构来说，按不考虑具体轨道结构形式模型计算所得的支点负弯矩最大值、跨中正弯矩最大值和支点剪力最大值均大于考虑具体轨道结构形式模型的相应值，并且随着地震动强度的增大，按2种模型计算所得的内力最大值差别有逐渐增大的趋势，例如在地震动峰值加速度为0.1g时，按考虑具体轨道结构形式模型计算所得的支点负弯矩最大值、跨中正弯矩最大值和支点剪力最大值分别为128 602.1 kN·m、36 683.8 kN·m、17 647.8 kN，按不考虑具体轨道结构形式模型计算所得的相应值分别为173 686.8 kN·m、75 970.1 kN·m、21 849.5 kN，差别分别为35.06%、107.09%、23.81%；而在地震动峰值加速度为0.4g时，按考虑具体轨道结构形式模型计算所得的支点负弯矩最大值、跨中正弯矩最大值和支点剪力最大值分别为167 556.2 kN·m、52 768.1 kN·m、23 956.8 kN，按不考虑具体轨道结构形式模型计算所得的相应值分别为228 615.3 kN·m、118 223.9 kN·m、34 064.4 kN，差别分别为36.44%、124.22%、42.19%。这主要是由于实际的高架轨道桥梁中轨道结构和主梁结构作为上部结构共同承担地震荷载的作用，即轨道结构本身也要承担相当的地震作用，而不考虑具体轨道结构形式的模型中完全忽略了轨道本身的承载作用，将由轨道结构本身承担的地震作用考虑为由桥梁主梁来承担。由此可见，对于桥梁的主梁结构来说，设计中不考虑具体的轨道结构形式是一种过于保守的偏安全的设计方法。为充分发挥主梁结构的强度，合理利用材料，节约资源，在进行轨道桥主梁结构设计时也应考虑轨道结构本身的承载作用。

3　结论

本文采用Midas civil软件建立了地震作用下高架轨道连续梁桥的有限元模型，分别按考虑与不考虑具体轨道结构形式2种情况，对其进行了地震响应时程分析，较系统地研究了弹性支承块式轨道结构对高架轨道桥梁地震响应的影响，得出的主要结论如下。

(1)对于高架轨道桥梁的桥墩结构来说，按不考虑具体轨道结构形式模型计算所得的桥墩墩顶顺桥向位移均小于考虑具体轨道结构形式模型的相应值，而桥墩墩顶位移的大小对桥梁结构整体倒塌起着举足轻重的作用。因此，在进行桥墩结构的抗震设计时，应考虑具体的轨道结构形式的影响。

(2)轨道结构可以加强高架轨道桥上部结构的整体刚度，因此，按不考虑具体轨道结构形式模型计算所得的连续梁桥主梁结构的各方向位移分量、各控制截面的内力值(支点负弯矩最大值、跨中正弯矩最大值和支点剪力最大值)均明显大于考虑具体轨道结构形式模型的相应值，且随着地震动强度增大，按2种模型计算所得的内力最大值差别有逐渐增大的趋势。由此表明，对于轨道桥梁的主梁结构来说，设计中不考虑具体的轨道结构形式是一种过于保守的偏安全的设计方法，为合理利用材料，在进行轨道桥主梁结构抗震设计时也应考虑轨道结构本身的承载作用。

[1]蔡成标，徐鹏.弹性支承块式无砟轨道结构参数动力学优化设计[J].铁道学报，2011，33(1)：69-75.

[2]吴天行.轨道减振器与弹性支承块或浮置板轨道组合的隔振性能分析[J]. 振动工程学报，2007，20(5):489-493.

[3]向俊，郭高杰，赫丹，等.弹性支承块式无砟轨道振动分析新模型[J].铁道科学与工程学报，2008，5(1):41-45.

[4]任勃，杨荣山，姜浩，等.CRTSΙ型板式无砟轨道梁端凸形挡台纵向力分析[J].铁道标准设计，2015，59(3):22-25.

[5]姜浩，赵坪锐，刘观.减振型无砟轨道轨枕结构对比分析[J].铁道标准设计，2014，58(10):51-56.

[6]李文斐，刘启宾.相邻墩高差对无砟轨道结构不平顺的影响研究[J].铁道标准设计，2015，59(9):22-25.

[7]尤瑞林，王继军，杜香刚，等.载铁路弹性支承块式无砟轨道轨距保持能力计算分析[J].铁道建筑，2015(3)：110-114.

[8]翟婉明，夏禾.列车-轨道-桥梁动力相互作用理论与工程应用[M].北京：科学出版社，2011:54-56.

[9]葛俊颖.桥梁工程软件Midas Civil使用指南[M].北京：人民交通出版社，2013：510-547.

[10]中华人民共和国住房和城乡建设部.GJJ166—2011城市桥梁抗震设计规范[S].北京：中国建筑工业出版社，2011.

[11]郭高杰.高速列车-弹性支承块式无碴轨道系统竖向振动分析[D].长沙：中南大学，2008.

[12]中华人民共和国铁道部.TB 10082—2005铁路轨道设计规范[S].北京：中国铁道出版社，2005.

[13]张婷.地震作用下高架轨道桥梁的动力响应分析[D].北京：北方工业大学，2013.

[14]蔡成标，徐鹏.高速铁路无砟轨道关键设计参数动力学研究[J].西南交通大学学报，2010，45(4):493-497.

[15]中华人民共和国住房和城乡建设部.GB50909—2014城市轨道交通结构抗震设计规范[S].北京：中国计划出版社，2014.

Seismic Performance Analysis of Elastic-block Supporting Rail Transit Bridge

HAN Yan

(College of Civil Engineering， North China University of Technology， Beijing 100141， China)

To study the influence of elastic-block supporting track structure on the displacement and internal force of bridge system under earthquake， a three-span continuous prestressed concrete box-girder elevated track bridge is referenced. The elevated track bridge finite element models are established with Midas Civil software respectively with and without the consideration of the specific form of track structures to analyze seismic responses of the viaduct subject to typical seismic waves. The results show that displacement of bridge girders， the positive moment at the mid-span， and the negative moment and shear force at the supported place indicated by the model with the consideration of the specific track structures are significantly less than the corresponding values from the model without. But， it is somewhat a safer design method without the consideration of the specific form of track structures as far as the main beam structure is concerned. Whereas， the pier top displacement calculated from the model considering the track structure may be larger than that from the model without considering the track structure. For the sake of safety， the specific form of track structures should be carefully considered in the seismic design of piers of track bridges．

Seismic response analysis; Elastic support block ballastless track; Finite element analysis; Track structure; Bridge pier

2015-12-08；

2016-01-06

北京市自然科学基金资助项目(8112013)

韩艳(1970—)，女，副教授，工学博士，E-mail：yanhanli@sohu.com。

1004-2954(2016)08-0073-06

U442.5+5

ADOI:10.13238/j.issn.1004-2954.2016.08.016