城市轨道交通轨道曲线超高计算及其程序实现
2016-10-21龙建兵刘郑琦
龙建兵,刘郑琦
(1.宁波市轨道交通集团有限公司,浙江宁波 315101; 2.中铁工程设计咨询集团有限公司,北京 100055)
城市轨道交通轨道曲线超高计算及其程序实现
龙建兵1,刘郑琦2
(1.宁波市轨道交通集团有限公司,浙江宁波315101; 2.中铁工程设计咨询集团有限公司,北京100055)
城市轨道交通存在着线路条件复杂、车辆变速较快、运营模式多样等特点,导致轨道曲线超高设计面临着诸多不同的复杂工况。在总结超高计算原则及超高要素限值的基础上,探讨单一速度模式、多种速度模式、缓和曲线进入有效站台等不同工况下超高计算方法并实现计算程序化,结论为:根据不同工况合理选择超高要素限值,单一速度模式宜采用平均速度法,多种速度模式宜采用优化的接近高速法,缓和曲线进入有效站台应以站台端部超高不大于15 mm作为限制条件,采用计算机语言实现超高计算程序化可有效提高设计效率。
城市轨道交通;曲线超高;超高要素;计算机程序
城市轨道交通线路条件复杂,列车在同一曲线范围内行车时,最高速度与最低速度往往存在着较大差异,加之线路不同定位决定了运营模式的不同,导致轨道交通轨道曲线超高计算面临着很多复杂工况。《地铁设计规范》(GB50157—2013)仅给出了超高的计算公式及最大超高、欠超高值,其他相关规范也没有明确的设计过程,对于工程中遇到的复杂工况例如近远期设计速度不同、快慢车模式、缓和曲线进入有效站台等没有明确的解决办法。本文在总结超高计算原则及超高要素(最大超高值、欠过超高、顺坡率等)限值的基础上,探讨了不同工况下超高计算方法及流程并实现计算程序化,为超高设计提供参考。
1 曲线超高计算原则
1.1超高计算公式
轨道交通车辆行驶于曲线上时,为平衡离心力[1],满足旅客舒适要求,提高线路的稳定性和安全性,曲线地段轨道结构需设置轨道超高[2]。
超高计算公式采用《地铁设计规范》(GB50157—2013)中7.2.3条有关规定[3],超高按下式计算
(1)
式中,h为超高值,mm;Vc为列车通过速度,km/h;R为曲线半径,m。
超高设置分为全超高和半超高,全超高采用内轨不动,外轨抬高超高值的方式,半超高采用内轨降低一半超高值,外轨抬高一半超高值的方式。为便于超高地段尤其是半超高地段的轨道施工,提高设置精度,降低施工难度,超高设计值宜取计算结果最近的偶数值。
1.2超高计算原则
城市轨道交通领域国家标准有《地铁设计规范》(GB50157—2013),行业标准有《城际铁路设计规范》(TB10623—2014),《铁路轨道设计规范》(TB10082—2005),《铁路线路修理规则》(铁运[2006]146号)等,还有各地地方标准等,不同的规范、地标对超高都有不同的规定、表述。
《地铁设计规范》7.2.3条规定,超高允许值[h]≤120 mm,欠超高允许值[hq]≤61 mm或[hq]≤75 mm(困难时)。
《城际铁路设计规范》条文说明5.2.2~5.2.4条规定[4],最大实设超高采用150 mm;欠、过超高允许值40 mm时舒适度为优秀、80 mm为良好、110 mm为一般;设计超高与欠超高之和允许值[h+hq]=180 mm时舒适度为优秀、210 mm为良好、240 mm为一般;欠超高与过超高之和允许值[hq+hg]=100 mm时舒适度为优秀、140 mm为良好、180 mm为一般。
《铁路轨道设计规范》3.0.3条规定[5],曲线外轨最大超高不应大于150 mm;3.0.5条规定,当设计速度v≤120 km/h时,欠超高允许值[hq]≤75 mm或[hq]≤90 mm(困难时),欠超高与过超高之和允许值[hq+hg]≤125 mm或[hq+hg]≤140 mm(困难时);另外,过超高允许值不宜大于欠超高允许值,即[hq]> [hg];过超高不宜大于50 mm,即[hg]≤50 mm。
另据《铁路线路修理规则》及国际铁路联盟(UIC)的有关资料,可设定过超高不宜大于50 mm,即[hg]≤50 mm[6]。
随着城市的发展,轨道交通的功能定位越来越多元化,不同的定位决定了设计标准例如设计速度的不同。《地铁设计规范》适用于最高运行速度不超过100 km/h的新建工程,那么,对于最高运行速度超过100 km/h的新建工程,应该在执行《地铁设计规范》的基础上,引入行业规范,综合考虑,统筹规划,在安全的前提下,满足各项要求。
2 曲线超高计算方法
列车通过曲线的速度不是固定不变的,超高计算的实质是为了取得一个合适的值:使最高速度满足欠超高要求,最低速度满足过超高要求[7]。
2.1单一速度模式
单一速度模式指的是行车具有唯一的设计最高时速。这样的模式在国内城市轨道交通中广泛存在,其曲线超高的主要计算方法有各点速度计算法[8],即通过选取列车在曲线几个关键点的运行速度来确定超高上下限,进而通过欠、过超高限值确定超高的合理范围。该方法具有操作简单、取值范围大等优点,但对于速度变化较快的曲线,其缺点是超高利用效率不足。总结各点速度计算法优点,引入平均速度来计算超高,在满足各项要求的基础上,使超高利用效率最大化。
(1)超高要素限值
单一速度模式最高运行速度多为80 km/h,执行《地铁设计规范》,并考虑到城市轨道交通为客运专用,参考工程实际[9],在设置曲线超高时,可采取以下设置方式:超高h≤120 mm,欠超高hq≤61 mm,过超高hg≤50 mm;超高顺坡率不宜大于2‰。
(2)超高计算
列车经过曲线时运行速度最大值为Vmax,最小值为Vmin,平均速度为V′,以上3个速度变量由行车专业提供。
已知曲线半径为R,通过公式(1)分别计算Vmax、Vmin、V′对应的超高hmax、hmin、h′。当h′≥120 mm时取h′=120 mm。暂取超高设计值h=h′,计算hq=hmax-h,hg=h-hmin,得到欠、过超高值。
根据hq和hg的值,按以下情况处理。
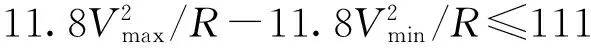
曲线范围内欠超高不会超过61 mm,过超高不会超过50 mm。设缓和曲线长度为ls,核算其超高顺坡率i,当i=h/ls≤2‰时,超高可取值为h=h′;当i≥2‰时,超高设置不合理,在h≥hmax-61的条件下降低超高值直至满足各项要求。
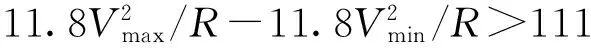
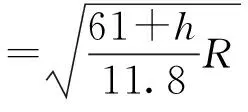
2.2多种速度模式
多种速度模式包括快慢车、远期提速等。快慢车模式指的是采用大站停列车(快车)与站站停列车(慢车)组合运营的模式[10],远期提速模式指的是设计初始就为线路远期进一步提速预留条件。多种速度模式时间效益和社会效益明显,其优点是对城市的快速发展适应性强,可有效满足不断提高的快速通勤要求。目前国内大城市郊区线、城际线等线路已经逐步采用该种运营模式,这对设计人员选择合理的超高提出了更高的要求。
对于快慢车模式,超高的设计应该同时满足快慢车行车需要,均衡快慢车欠、过超高。对于远期提速模式,超高的设计可以采用先满足近期后改造,也可采用一步到位兼顾近远期行车需要,但城市轨道交通轨道结构多采用整体道床,后期超高改造费工费时[11],故多采用一步到位法。综上所述,兼顾快慢车(或近远期运营速度)超高设计推荐采用兼顾2种运行速度的设计方法,有临界法和接近高速法。临界法[12]是利用超高允许值,欠、过超高允许值等要素限值来定义超高的上下限,在此范围内再进一步确定设计超高,该方法的优点是可最大范围满足不同模式快慢车的共线运营。接近高速法是在满足慢车(或近期运营速度)的前提下,尽量取接近快车(或远期运营速度)的超高,该方法可满足大部分快车旅客舒适度要求,同时在设计中预留了进一步提速条件。
多种速度模式多用于郊区线、市域线,随着城市的发展,跨区域的轨道交通会迎来良好的发展契机[13],此外,乘客对于旅行速度、舒适度的要求必然会越来越高,综合考虑推荐采用接近高速法,并引入平均速度优化计算。
2.2.1超高要素限值
(1)超高时变率对超高的影响
《地铁设计规范》条文说明6.2.2 第3款中,提出了限制车轮升高速度的超高时变率f是满足乘客舒适度的一项指标,设曲线运行速度最大值为Vmax,可知f=(h·Vmax)/(3.6·ls)≤40 mm/s。对于最高运行速度不超过100 km/h的地铁新建工程,由《地铁设计规范》6.2.2条可知,限制超高最大值为120 mm可保证超高时变率不超标。但对于快车(或远期运营速度)最高运行速度超过100 km/h的地铁新建工程,若提高最大超高必然会导致线路内个别缓和曲线长度不足的曲线超高时变率超标,故对于多种速度模式,需验算超高时变率。
(2)超高限值分级
《地铁设计规范》是城市轨道交通设计的国家规范,对于最高运行速度超过100 km/h的地铁新建工程,规范中关于超高、曲线要素的部分规定将不再适用[14],应该在执行该规范的同时,参考其他行业规范,综合考虑,统筹规划。对于多种速度模式,在设置超高时,可根据曲线运行速度最大值Vmax采取分类、不同标准设置方式。
①对于Vmax≤100 km/h,考虑到提高超高最大值将对各专业产生影响[15],执行《地铁设计规范》,超高h≤120 mm,欠、过超高hq≤61 mm、hg≤50 mm。
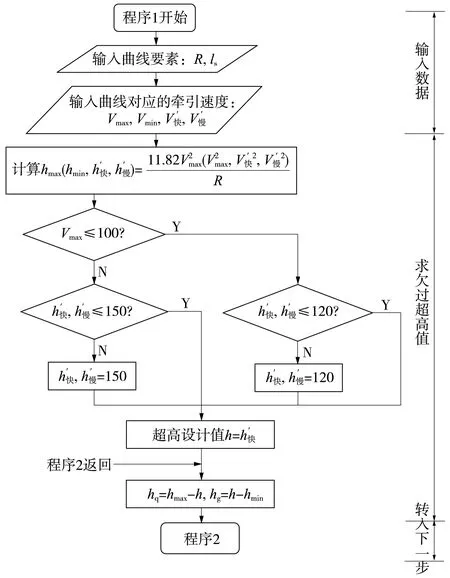
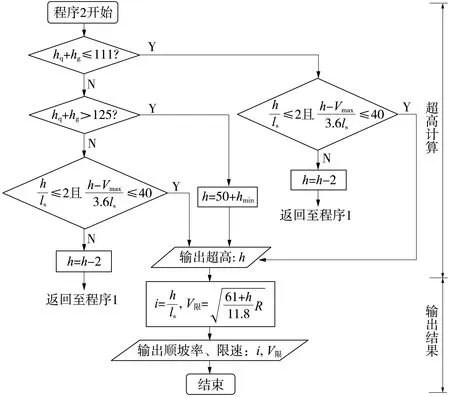
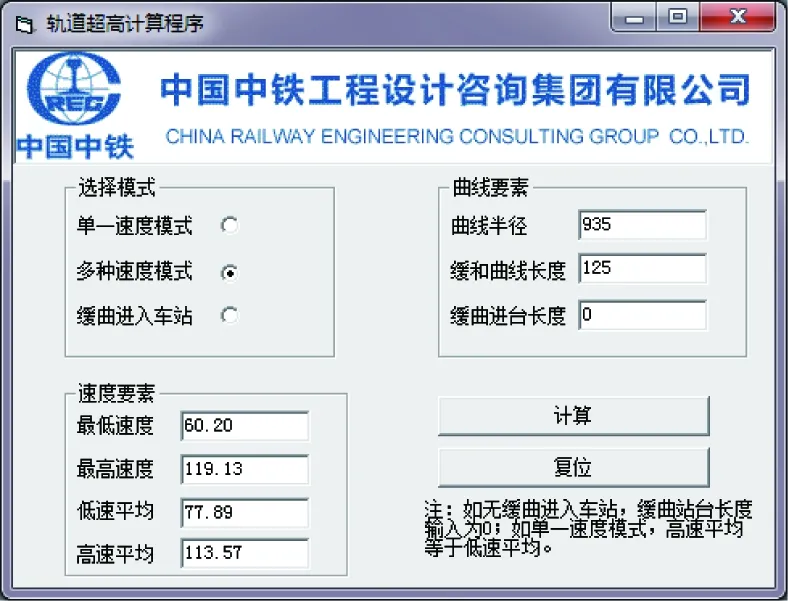
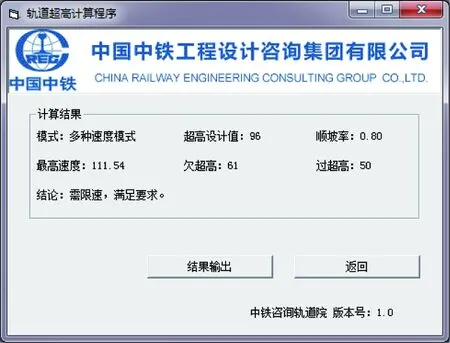
②对于100 km/h 此外,超高顺坡率不宜大于2‰,困难地段不应大于2.5‰,超高时变率不宜大于40 mm/s。 2.2.2超高计算 在多种速度模式下,对慢车(或近期运营速度)来说,其通过曲线时过超高允许值应成为其检算限值,对快车(或远期运营速度)来说,其通过曲线时欠超高允许值应成为其检算限值。 根据hq和hg的值,按以下情况处理。 超高不能同时满足过超高和欠超高要求,需限速,此时,超高计算应优先满足过超高要求,在h≤50 mm+hmin的条件下提高超高值,以满足各项要求并尽可能提高限制速度加大列车通过效率。 2.3缓和曲线进入车站有效站台 《地铁设计规范》7.2.3条规定:车站站台有效长度范围内曲线超高不应大于15 mm。当缓和曲线进入车站有效站台范围内时,站台端部超高h端≤15 mm即为限制条件。 计算步骤应按上文所述先计算超高h1,超高顺坡率i1=h1/ls,则站台端部曲线超高h端=s×i1,其中s为缓和曲线进入有效站台长度。 根据h端的值,按以下情况处理。 (1)当h端≤15 mm 时,缓和曲线进入有效站台对超高计算没有影响,超高可取值为h=h1。 (2)当h端>15 mm时,缓和曲线进入有效站台对超高计算有限制,这时需取h端=15 mm,反算超高顺坡率i2=15 mm/s,则超高h2=ls×i2,验证超高h2是否满足欠、过超高要求,如满足,超高可取值为h=h2,如不满足需限速。 不同工况下进行超高计算应先确定合适、合理的超高要素限值,根据曲线半径、缓和曲线长度等曲线要素及行车速度等条件计算超高,再将超高值返回验证是否满足超高要素限值,如满足则取其为超高设计值,不满足则根据限值条件返回重新计算直至满足要求。以多种速度模式为例,结合计算机语言,对超高计算程序化设计。程序分为两部分即程序1、程序2,程序1主要功能为设计输入、限值确定;程序2主要功能为超高计算、超高验证、设计输出,其程序流程如图1和图2所示。 图1 超高计算程序流程(程序1) 图2 超高计算程序流程(程序2) 计算机编程语言有C语言、C++语言、VB语言等,本文以VB语言为平台,实现超高计算程序化。本程序集成了单一速度模式、多种速度模式、缓和曲线进入车站有效站台等3种不同工况,利用前文所述计算流程对超高计算实现程序化、智能化。 以广州地铁21号线为例,该工程为快慢车运营模式,即多种速度模式,选取某一曲线,先按优化的接近高速法进行计算,过程如下。 (3)已知hq+hg=134 mm>125 mm,暂取的超高设计值不能同时满足过超高和欠超高要求,需限速。此时,超高计算应优先满足过超高要求,超高设计值取值范围为h≤50 mm+hmin=96 mm,取为96 mm,限速V限=111.54 km/h。 (4)计算超高顺坡率i=0.8‰≤2‰,超高时变率f=23.80 mm/s≤40 mm/s,满足要求。 综上所述,该曲线需限速V限=111.54 km/h,超高设计值取h=96 mm,超高顺坡率i=0.8‰,超高时变率f=23.80 mm/s,欠、过超高值hq=61 mm,hg=50 mm。 利用超高计算程序计算上例,操作界面包括模式选择、曲线要素输入、速度要素输入等分界面,选择“多种速度模式”,分别输入曲线要素、速度要素,如图3所示。输入参数后,点击计算按钮进行超高“拟合”计算,计算过程同程序流程图,结果输出界面包括超高设计值、顺坡率、最高速度(限速值)等结论,如图4所示。 图3 超高计算程序操作界面 图4 超高计算程序结果输出界面 根据前述不同工况下的超高计算过程,编辑程序流程图,实现超高计算程序化可保证计算结果的准确性,不仅避免了人工计算可能出现的错误,还能大大提高设计效率。 本文在总结超高计算原则及超高要素限值的基础上,探讨了单一速度模式、多种速度模式、缓和曲线进入有效站台等不同工况下超高计算方法及流程,并实现超高计算程序化,主要结论如下。 (1)单一速度模式推荐采用平均速度法,通过平均速度计算出的超高在满足超高要素限值的基础上,可使超高利用效率最大化。 (2)多种速度模式推荐采用优化的接近高速法,在满足慢车(或近期运营速度)的前提下,尽量取接近快车(或远期运营速度)的超高,可满足大部分快车旅客舒适度要求,同时在设计中预留了进一步提速条件。 (3)对于缓和曲线进入车站有效站台,应按计算流程先行计算超高及站台端部超高,以站台端部超高不大于15 mm作为限制条件。 (4)超高计算是在各项超高要素限值的限制下进行的“拟合”计算,故采用计算机编程语言将超高计算程序化,可大大提高设计效率。 [1]于春华,杨其振.城轨交通曲线未被平衡离心加速度容许值的探讨[J].铁道标准设计,2007(8):20-23. [2]李成辉.铁路轨道[M].北京:中国铁道出版社,2012. [3]中华人民共和国住房和城乡建设部.GB50157—2013地铁设计规范[S].北京:中国建筑工业出版社,2013. [4]铁道第三勘察设计院集团有限公司,中铁第四勘察设计院集团有限公司.TB10623—2014城际铁路设计规范[S].北京:中国铁道出版社,2014. [5]中华人民共和国铁道部.TB10082—2005铁路轨道设计规范[S].北京:中国铁道出版社,2005. [6]杨其振.城市轨道交通曲线轨道超高有关问题探讨[J].铁道勘察,2005,31(2):7-9. [7]尹华拓,罗信伟,宋嘉雯.快慢车运营模式时速120 km线路的轨道超高设置[J].铁道勘察,2014(4):81-83. [8]黄红东.城市轨道交通曲线最大超高值设置浅析[J].铁道标准设计,2007(7):13-16. [9]谭代明,伍丽蓉,向海波,等.珠三角城际轨道交通曲线超高设置研究[J].铁道建筑,2013(7):129-132. [10]宋键,徐瑞华,缪和平.市域快速轨道交通线开行快慢车问题的研究[J].城市轨道交通研究,2006(12):23-27. [11]刘建成.武汉至黄石城际铁路超高设置研究[J].铁道建筑技术,2010(8):60-62. [12]王维.铁路客运专线轨道超高设置的适应性研究[J].铁道标准设计,2014(3):15-21. [13]杨舟.我国市域轨道交通发展策略研究[J].铁道标准设计,2013(5):27-30. [14]孔凡兵.新建时速120 km地铁线路曲线超高和缓和曲线长度的研究[J].铁道标准设计,2015(9):18-21. Rail Curve Superelevation Calculation and Program Realization of Urban Mass Transit LONG Jian-bing1, LIU Zheng-qi2 (1.Ningbo Railway Transit Group Co., Ltd, Ningbo 315101;2.China Railway Engineering Consulting Group Co., Ltd., Beijing 100055, China) Due to the complicated route condition, rapid vehicle speed variation, and diversified operation modes, elevation design of rail curve is faced with complicated working situations. Based on the design principles for super elevation calculation and superelevation factor limits, this paper focuses on superelevation calculation methods and program realization under such working conditions as single-speed mode, multi-speed mode, and easement curve entering platform. The results show that superelevation factor limits are selected according to different working conditions. Average speed method should be adopted for single speed mode. For multi-speed mode, optimized approaching high speed method should be adopted. In order to ease the curve entering effective platform, 15 mm should be taken as the restriction for the end platform superelevation. Using computer programming may effectively improve the design efficiency. Urban mass transit; Rail curve superelevation; Superelevation factors; Computer program 2015-12-28; 2016-01-08 龙建兵(1971—),男,高级工程师,1995年毕业于长沙铁道学院,工程硕士,E-mail:tsyljb@126.com。 1004-2954(2016)08-0001-05 U213.2 ADOI:10.13238/j.issn.1004-2954.2016.08.001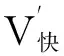
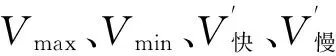
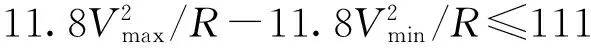
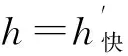
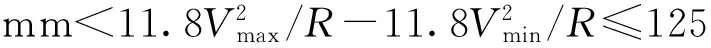
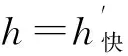
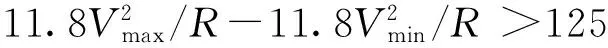
3 曲线超高计算程序实现
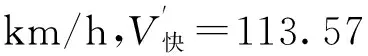
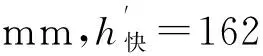
4 结论
