基于Hvorslev模型的微水试验应用
2016-10-21张昌新
张昌新
(铁道第三勘察设计院集团有限公司,天津 300142)
基于Hvorslev模型的微水试验应用
张昌新
(铁道第三勘察设计院集团有限公司,天津300142)
对Hvorslev模型进行分析,介绍利用微水试验测定渗透系数的计算公式。实际工程对比试验结果表明,基于Hvorslev模型的微水试验结果与常规抽水(注水)试验结果接近,说明该方法能满足工程需求,可在工程勘察中推广应用。
微水试验Hvorslev模型渗透系数
在目前的岩土工程勘察工作中,准确查明地基土的透水性质成为勘察工作的重点和难点,地层渗透系数也是影响工程设计、施工的关键参数。
微水试验(Slug Testing)由外国学者Hvorslev于20世纪50年代初首次应用,目前又被称为重锤试验、冲击试验和定容积瞬息抽水试验等,它通过观测井内水位瞬时改变后水位随时间的变化情况来求得井附近含水层的水文参数。瞬时改变水位的方法有瞬时向井内注入(抽出)一定量的水,也可以向井内插入或取出一定长度圆柱体。
该方法与目前普遍采用的抽(注)水试验相比,仅需少量的时间、人力、经费。微水试验一般仅需1 min~几小时即可完成,而抽(注)水试验需要的时间往往长达几天甚至十几天。
该试验方法的适用性及精确性已经过外国学者多年的实际经验验证,但国内的实际应用仍然较少。
尽管微水试验方法所求得的渗透系数只能反映出试验孔附近小范围含水层介质的性质,但在实际应用中,可以通过增加试验点来获得较大范围内的渗透系数。
1 Hvorslev模型
1.1基本原理
Hvorslev在1951年通过大量试验后发现井内水位迅速变化后水位恢复的速度和时间成指数关系,水位恢复的时间与地层的渗透系数有关,恢复速率与井孔的结构有关。在此基础上,Hvorslev针对承压完整和非完整井的过阻尼微水试验提出一种半解析的方法(如图1所示)。
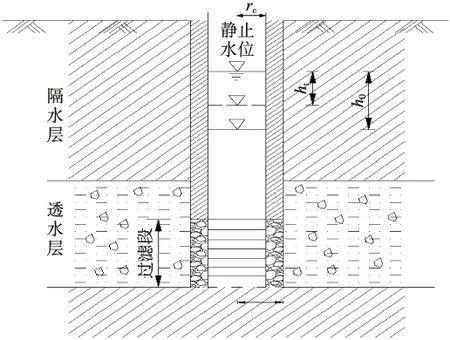
图1 井孔结构
针对承压含水层中的地下水,Hvorslev发现当井孔中的地下水位瞬时改变后,流出或流进井孔的水流量与井孔附近含水层渗透系数之间的关系可表示为
(1)
式中rc——套管半径;
F——形状因子,取决于井孔滤水管形状和位置;
Kr——影响半径内的含水层水平渗透系数;
h0——t=0时静止水位到井孔水位间的距离;
y——试验过程井孔中水位的变化量;
h0-y——试验过程中静止水位到井孔水位间的距离。
对(1)式分离变量,得
(2)
对(2)式定积分
因此
(3)
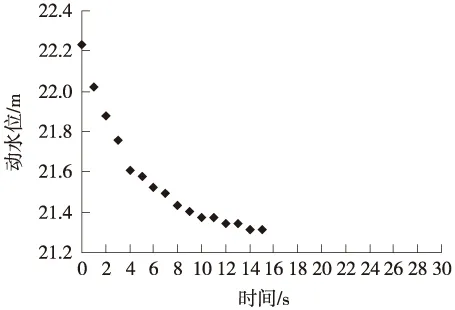
数据来源:邢台08-ZD-1824号孔微水试验图2 试验数据
因此式(3)可变为
水平渗透系数
(4)
其中形状因子F根据过滤管与含水层的相对位置可分为三种情况,只要求得F就可以求得渗透系数。
1.2形状因子F的确定
根据过滤管与含水层的相对位置,可分为三种情况(如图3所示)。
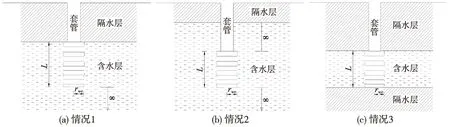
图3 过滤管与含水层的三种情况
(1)第一种情况
如图3(a),非完整井,过滤管顶部或底部毗邻含水层顶板或底板。一般过滤管长度小于整个含水层厚度的80%,即可认为属于非完整井。而如果含水层边界距离过滤管一端的距离小于过滤管长度的10%,即可认为是毗邻的。
Hvorslev形状因子通过如下公式计算
(5)
其中:
F——形状因子;
L——静止条件下饱和含水层中过滤管长度;
rwe——过滤管有效半径(过滤管半径与过滤层厚度之和)。
(2)第二种情况
如图3(b),非完整井,过滤管顶部或底部距离含水层顶板或底板较远,即含水层顶部和底部并不在试验影响区域内。一般过滤管长度小于整个含水层厚度的80%,即可认为属于非完整井。而如果含水层边界距离过滤管一端的距离大于过滤管长度的10%,即可认为是相距较远。
Hvorslev形状因子通过如下公式计算
(6)
(3)第三种情况
如图3(c),完整井,过滤管穿透整个饱和含水层。当过滤管的长度大于过滤管有效半径8倍时,即L/rwe>8,Hvorslev形状因子通过如下公式计算
(7)
其中:
R——微水试验的影响半径。
在计算第三种形状因子公式中,需要估算微水试验的影响半径R,国外学者通过大量研究,建议取过滤管的长度或200rwe。本文采用后一种方法,因为对于一般完整井,过滤管的长度一般要比过滤管半径大几十到几百倍,取对数后的数值变化很小。
1.3数据分析
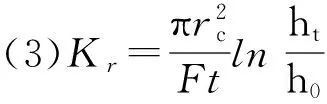
数据分析的基本步骤如下:
(1)将实测数据画在半对数坐标轴上,y轴为log(ht/h0),x轴为时间t;
(2)利用最小二乘法对(t,lg(ht/h0))数据进行拟合,求出直线方程,见图4。
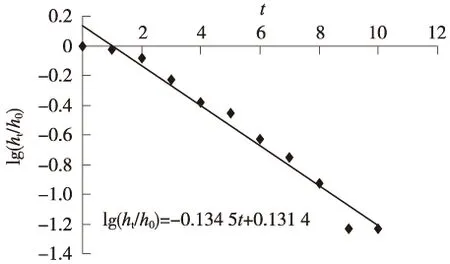
图4 对(t,lg(ht/h0))进行直线拟合
(3)根据直线公式确定ht/h0=0.37的时间t,即为基本时间间隔TL,将直线绘制在半对数坐标系中(如图5)。

图5 半对数坐标系中的直线拟合
(4)再将三种情况下的形状因子F代入(4)式,即可得到三种情况下的渗透系数计算公式。
第一种情况下
(8)
其中:
rc——套管半径;
rwe——过滤管有效半径(过滤管半径与过滤层厚度之和);
Kr——影响半径内的含水层水平渗透系数;
L——静止条件下饱和含水层中过滤管长度;
TL——基本时间间隔(ht/h0=0.37的时间t)。
第二种情况下
(9)
第三种情况下
(10)
其中:
R——微水试验的影响半径,可取200rwe。
2 应用实例
2.1微水试验1-京沪高速铁路
试验点位于济南玉符河特大桥08-ZD-8289-7号孔,进行潜水层抽水试验和微水试验,地层与井孔结构如图6。
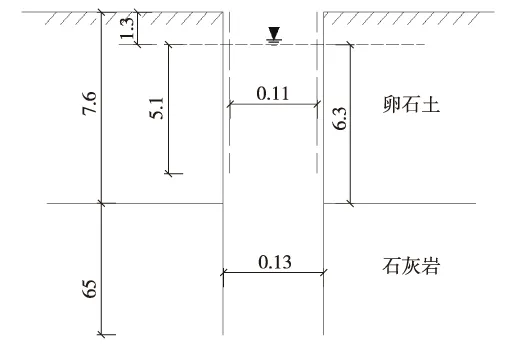
图6 井孔结构(单位:m)
井孔深65 m,7.6 m之上为卵石土,之下为石灰岩,7.6~12.6 m较破碎,12.6 m之下较完整。花管从井口向下,长6.4 m。考虑到7.6~12.6 m石灰岩裂隙较发育,有效进水段长度为6.3 m+5 m=11.3 m,属完整井稳定流抽水试验,井孔结构参数如表1。

表1 井孔结构参数 m
抽水井资料与计算的渗透系数如表2。

表2 渗透系数计算结果
随后进行了简单微水试验,包括提水和注水,利用Hvorslev法进行计算,计算结果如表3。
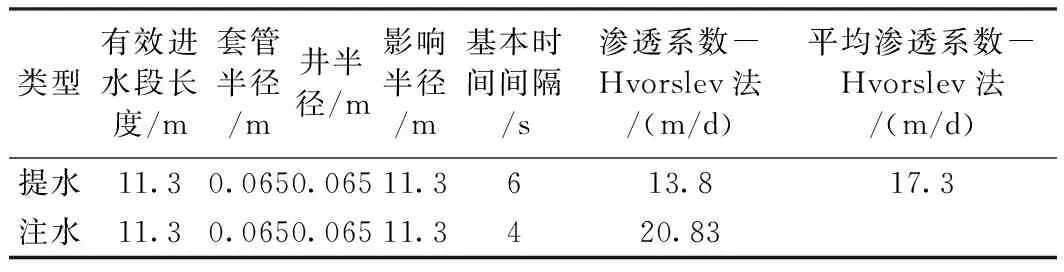
表3 微水试验计算结果
2.2微水试验2-太中银铁路
试验点位于太原路改桥1号特大桥08-ZBD-TY073号孔,对潜水层进行提水试验和微水试验,地层和井孔结构如图7所示。
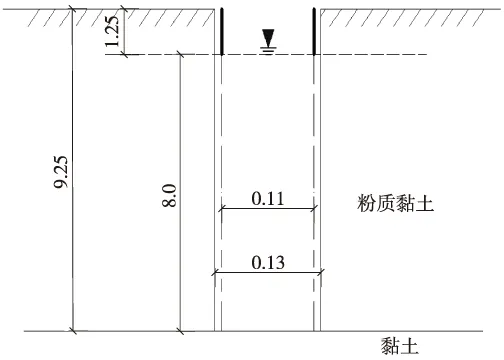
图7 井孔结构(单位:m)
井孔深9.3 m,潜水赋存于粉质黏土中,进行提水试验,井孔结构参数见表1。
利用水位恢复资料计算渗透系数,公式为
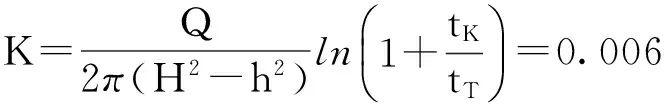
随后进行简单微水试验,利用Hvorslev法计算K=0.007 96(m/d)。
2.3微水试验3-石郑客专
试验点位于邢台榆林洺河特大桥08-ZD-1824号孔,对第一层承压水进行抽水试验和微水试验,地层与井孔结构如图8。
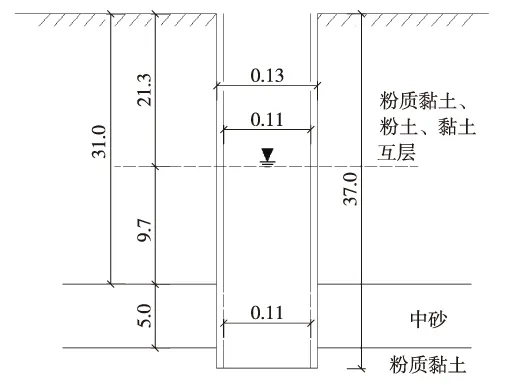
图8 井孔结构(单位:m)
井孔深37 m,属完整井稳定流抽水试验,井孔结构参数见表1。
利用裘布依完整稳定流公式计算渗透系数K=30.83(m/d),随后进行简单微水试验(提水和注水),利用Hvorslev法计算K=32.272(m/d)。
3 结论
(1)通过对比试验,常规抽(提)水试验结果与微水试验结果接近,说明微水试验成果满足工程设计需要,可在工程勘察中推广应用。
(2)微水试验能大幅度缩短试验周期,减少现场试验需要的设备,减轻现场技术人员的工作负担,降低水文试验费用。
(3)微水试验影响半径小,仅代表小范围地层的渗透系数值,而抽水试验影响半径较大,得到的渗透系数能代表更大范围地层的平均值。
[1]Hvorslev M J. Time Lag and Soil Permeability in Ground-Water Observations, Waterways Exper. Sta. Corps of Engrs, Bull. 1951(36):1-50
[2]BOUWER H,RICE R C. A slug test for determining hydraulic conductivity of unconfined aquifers with completely or partially penetrating wells[J]. Water Resources Research, 1976,12(3):423-428
[3]Bouwer H. The Bouwer and Rice slug test-an update[J]. Ground Water, 1989,27(3):304-309
[4]独仲德,马炳辉,姚来根,等.确定含水层渗透系数的冲击试验方法[J].水科学进展,2003,14(6)
[5]中国地质调查局.地文地质手册[M].北京:地质出版社,2012
[6]陈则连.水文地质试验技术应用研究[J].铁道勘察,2009,35(1)
[7]原国红,马琳.水文地质参数自动监测处理系统的研制与应用[J].岩石力学与工程学报,2009,28(4):834-839
[8]薛禹群.地下水动力学原理[M].北京:地质出版社,1986
[9]中华人民共和国铁道部. TB10049—2004铁路工程水文地质勘察规程[S].北京:中国铁道出版社,2002
[10]苏锐,王驹,等.斯拉格.试验技术与理论研究综述[J].岩石力学与工程学报,2007,26(2):3882-3890
[11]余学鹏,门妮.完整井稳定流抽水试验渗透系数的确定分析[J]. 铁道勘察,2010,36(6)
[12]汪继锋.隧道深孔水文地质试验方法[J].铁道勘察,2004,30(4)
Applicatin of Slug Testing Based on Hvorslev Mode
ZHANG Changxin
2016-01-20
张昌新(1965—),男,1986年毕业于西南交通大学工程地质专业,工学硕士,高级工程师。
1672-7479(2016)02-0016-04
P641
A
