基于MATLAB/Simulink和ADAMS的拖拉机建模与振动仿真分析

程准，王俊，鲁植雄

（南京农业大学工学院，江苏 南京 210031）

基于MATLAB/Simulink和ADAMS的拖拉机建模与振动仿真分析

程准，王俊，鲁植雄*

（南京农业大学工学院，江苏 南京 210031）

基于多体动力学研究的理论和方法，利用MATLAB和ADAMS软件分别建立JS-754拖拉机振动的数学模型和机械模型，进行随机振动和脉冲输入的平顺性仿真分析。数学模型包括利用拉格朗日第二方程建立拖拉机3自由度振动模型，从轮胎动态特性出发，建立拖拉机整车—轮胎耦合系统；机械模型借助虚拟样机技术对JS-754拖拉机整车实体建模，并定义整车各个部件约束关系。仿真结果表明，JS-754拖拉机在D级路面下座椅处垂向加速度均方根值为0.390 9 m/s2，脉冲激励输入下座椅处垂向加速度最大响应小于34.59 m/s2。仿真得到轮胎特性随车行驶时变化曲线，座椅处振动频率的范围集中在3-5 Hz。研究表明，JS-754拖拉机平顺性较好，提出的拖拉机振动建模方法具有较强的参考价值，可为拖拉机以及其他非道路车辆平顺性的研究提供理论依据和建模思路。

拖拉机；多体动力学；振动；模型；虚拟样机

程准， 王俊， 鲁植雄. 基于MATLAB/Simulink和ADAMS的拖拉机建模与振动仿真分析［J］. 农业现代化研究， 2016， 37（2）：395-401.

Cheng Z， Wang J， Lu Z X. Tractor modeling and its vibration analysis based on MATLAB/Simulink and ADAMS［J］.

Research of Agricultural Modernization， 2016， 37（2）： 395-401.

拖拉机有着一定的特殊性，拖拉机一般没有悬架［1］，已有研究表明，驾驶人员在拖拉机上工作时所承受的振动加速度可能要比汽车司机承受的大几倍甚至更多［2］。拖拉机平顺性的优劣对工作效率、乘员健康、机体以及各零部件的寿命等均会产生直接的影响，所以拖拉机平顺性的研究意义深远。

国内基于虚拟样机技术对拖拉机整车平顺性的研究较少［3-4］，国外研究人员对拖拉机驾驶舒适性及对人体的影响做了不少研究［5-7］。当轮式拖拉机在地面上正常行驶或在田间工作时，由于拖拉机发动机曲轴的旋转和活塞的往复造成的内部激振和外界路面的激励，使得拖拉机的轮胎和地表路面之间会发生彼此相互的振动，这会导致车辆轮胎的力学特性发生改变，而对于拖拉机这种一般无弹性悬架的车辆来说，其轮胎是非常重要的减振元件，所以拖拉机轮胎的动态特性在很大程度上决定了拖拉机的平顺性。然而研究人员通常都是利用轮胎的静态特性［8-9］来进行平顺性仿真研究，显然并不符合实际工况。而且，轮胎动态特性变化影响整车垂向振动，整车的垂向振动又会反作用于轮胎，这是一个耦合的过程。文中采用拉格朗日法对JS-754拖拉机振动模型进行构建，基于MATLAB以轮胎动态特性建立动力学模型并在标准的D级随机激励路面下进行了仿真；建立针对拖拉机脉冲输入的评价指标，并对基于ADAMS建立的整车模型进行脉冲激励输入下的仿真，以期为今后拖拉机以及其他非道路车辆平顺性和振动特性的研究提供理论及建模思路。

1 拖拉机平顺性评价方法

1.1 随机激励下的拖拉机平顺性评价方法

对于平顺性的研究，道路、车辆和人是作为一体来分析的，虽然人的主观感受是其中的关键，但是由于乘员人体之间的差异再加上人员心理和生理的复杂作用使得主观评价法存在很大的缺陷。ISO 2631是众多客观法中的一种，借助于科学计算的手段针对人体承受来自车辆的振动进行评价，适用的振动频率范围为0.5-80 Hz。常用的评价指标有总加权加速度均方根值和1/3倍频带法，根据ISO 2631，本文采用的是加权加速度均方根值来评价车辆的平顺性（表1）。

表1 人主观感受的分类Table 1 Classification of human subjective feelings

1.2 脉冲激励下的平顺性评价方法

对于拖拉机这种非道路车辆来说，在实际行驶时经常会遇到凸包等障碍，所以对拖拉机进行脉冲输入的平顺性研究具有特殊意义。GB 5902—86为车辆在脉冲路面行驶振动的研究提供了相应的试验标准和理论依据，根据余志生［10］、赵六奇和刘锋［11］以及ISO 2631新草案的内容，建立对应所要研究拖拉机的脉冲输入平顺性的客观评价方法。

根据高树新和宫镇［12］提出的脉冲输入平顺性评价指标计算公式为：

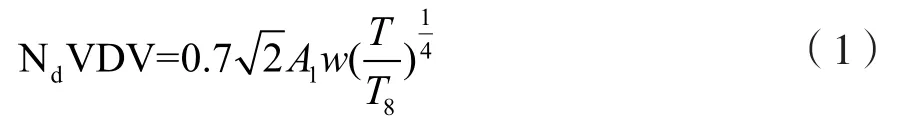
式中：NdVDV为振动剂量值；T为暴露时间（s），T=1/f；f为座椅系统固有频率（Hz）；T8按照ISO 2631，取值为28 800 s；A1表示加速度最大响应值（m/s2）；表示座面垂直方向上频率加权函数，当0.5＜f＜2.0时，w=0.4。

针对拖拉机装有弹簧和减振器的座椅系统，f 取1.5 Hz［13］，故w=0.4。ISO 2631规定，当振动剂量值大于1.30时会对健康产生危害；当振动剂量值在0.95到1.30之间时会对健康造成一定程度的影响；当振动剂量值小于0.95时，则可以认为不会对健康造成危害。故推导出的临界值为：

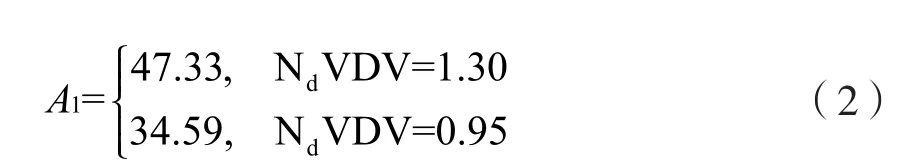
综上所述，若座椅处垂直振动的最大值大于47.33 m/s2则会对乘员健康产生危害，若小于34.59 m/s2则不会对乘员健康造成影响，如果座椅处垂直振动在时域中最大加速度介于34.59-47.33 m/s2之间，则对健康会产生一定的危害，而且危害程度随着数值的增大会上升。

2 拖拉机仿真模型的建立

2.1 基于拖拉机轮胎动态特性的“车—轮胎”耦合随机振动仿真模型

2.1.1 拉格朗日法建立拖拉机自由振动方程 假定拖拉机关于其纵向轴线对称，且其行驶过程中，左右车轮所经历的路面情况相同，将拖拉机模型简化为半车模型。模型建立的准确度关系着整个仿真分析的成败［14］。由于本文研究的是拖拉机直线行驶时的平顺性，考虑拖拉机特殊的工作性质，并从实际对于模型简化研究所需的要求和提高仿真的精度出发［15］，建立拖拉机3自由度半车振动模型（图1），其具有2个输入为半车模型的前、后车轮所接受的路面激励，且后轮随机激励的输入较前轮滞后一段时间，3个自由度分别为拖拉机车体质心处垂直方向的振动、车体绕质心横轴的俯仰振动和驾驶员座椅处的垂直振动。

拉格朗日第二方程用广义坐标表示动力方程，简化力学问题，适用于完整复杂系统［16］，表达式为：

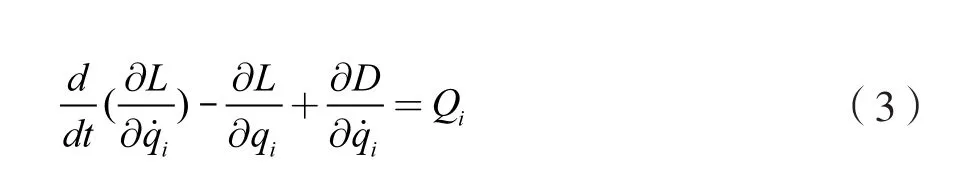
式中：q为广义坐标；L=T-U，即动能与势能表达式之差（J）；D为耗散能（J），通常指阻尼元件损耗的能量；Qi为广义力（N）。

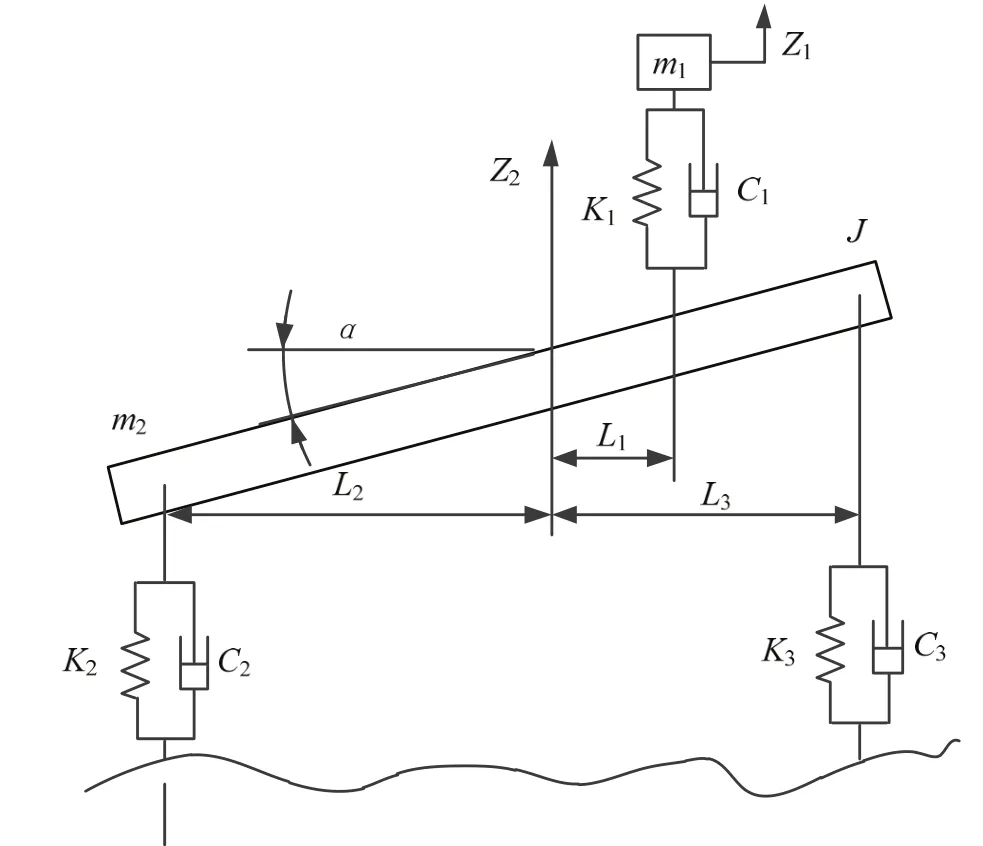
图1 拖拉机半车振动模型Fig. 1 Half-tractor vibration model

由于俯仰角α振动较小，故取sinα≈α，则系统动能为：

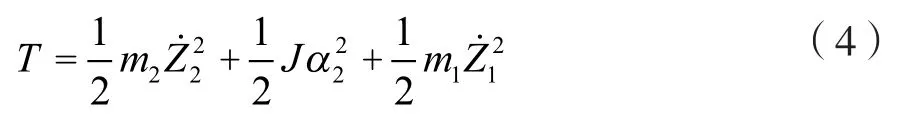
系统势能为：

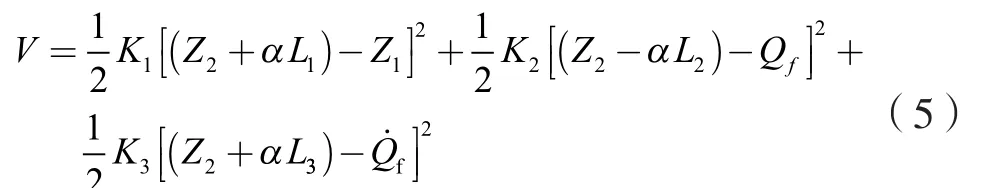
系统耗散能为：

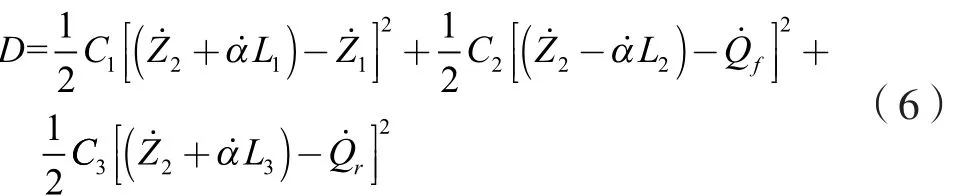
2.1.2 拖拉机轮胎动态特性的数学模型 轮胎的刚度和阻尼系数都与轮胎的气压和荷重质量有关［17］，其中气压影响最大，而荷重是先改变气压的大小以及气压在胎内的分布再间接影响刚度和阻尼的变化。

仿真模型选择CF700拖拉机轮胎，型号为6.5-20 和14.9-30，根据该轮胎特性随气压变化的数据［18］，拟合该轮胎特性的计算公式为：

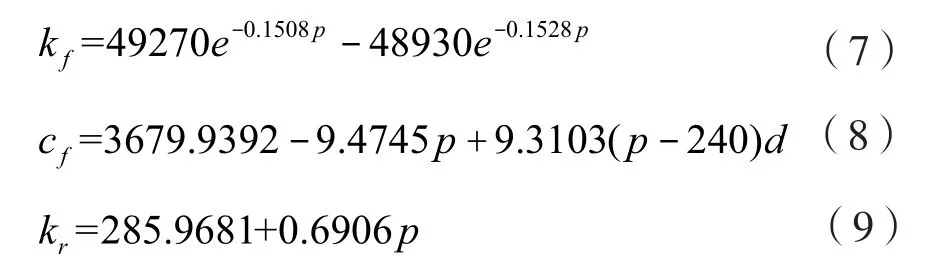
式中：kf、kr为前、后轮胎的刚度（kN/m）；cf、cr为前、后轮胎的阻尼（N·s/m）；p为轮胎气压（kpa）。

轮胎气压的值在实际拖拉机行驶时也是不断变化的，其与滚动速度、轮胎的初始充气压力、温度和载荷有关。拖拉机行驶时轮胎气压计算方法［19］为：

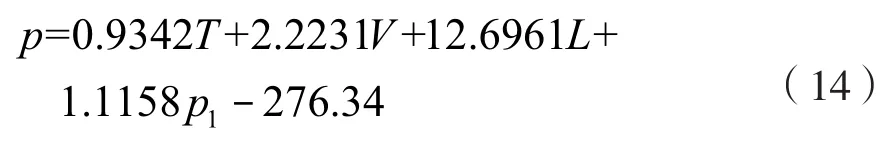
式中：T为环境温度（℃）；V为行驶速度（km/h）；L为载荷（kN）；p1为初始气压（kpa）。

2.1.3 Simulink随机振动仿真模型 随机振动的平顺性仿真所选取的主要参数为：v=30 km/h， K1=24.2 kN/m， C1=1 470 Ns/m， m1=65 kg， m2=2 935 kg， J=3 547.2 kg·m2， L1=0.4 m， L2=1.315 m， L3=0.8 m。通过滤波白噪声法建立随机路面模型，路面等级选择为D级。整车参数主要来自JS-754拖拉机的整车参数，座椅系统的刚度和阻尼特性参考相关拖拉机座椅系统［20］进行选取。

结合公式（7）-（14），引入轮胎动态特性，并基于MATLAB/Simulink建立“路面随机激励—拖拉机—轮胎”的耦合关系模型（图2）。

2.2 基于ADAMS的JS-754拖拉机脉冲输入平顺性仿真模型

利用PRO/E建立拖拉机整车机械模型。基于虚拟样机技术的拖拉机平顺性仿真研究在国内较少，大部分的研究人员在建立拖拉机动力学模型时都是做了大量的简化工作［4］。除去车轮外，一般都将拖拉机简化为前轴、后轴和车架模型。因为该拖拉机没有悬架，所以在建模的时候利用ADAMS/View工具箱里面的固定副使拖拉机前轴、后轴和车架刚性的连接在一起，建立了拖拉机整车动力学模型（图3）。该拖拉机的平顺性完全依靠轮胎的振动特性和座椅系统的振动特性以及整体的结构来体现。为了模拟“人—座椅”系统，将此系统简化为一个质量块，取65 kg作为该质量块的有效质量。座椅系统的刚度和阻尼特性通过添加ADAMS/View中Flexible Connections的SPRING_DAMPER来实现。

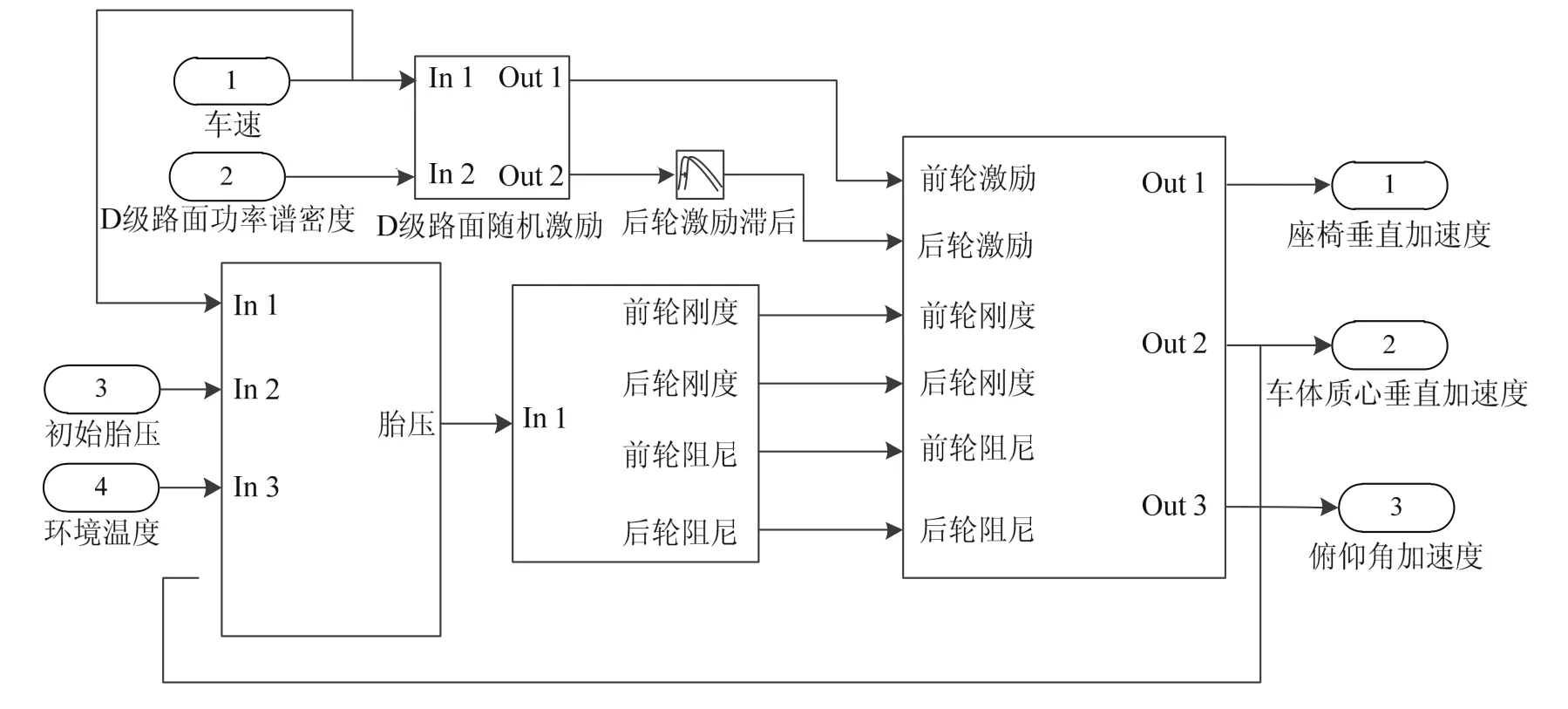
图2 “车—轮胎”耦合随机振动仿真模型Fig. 2 The random vibration simulation model of the tractor-tire coupling system

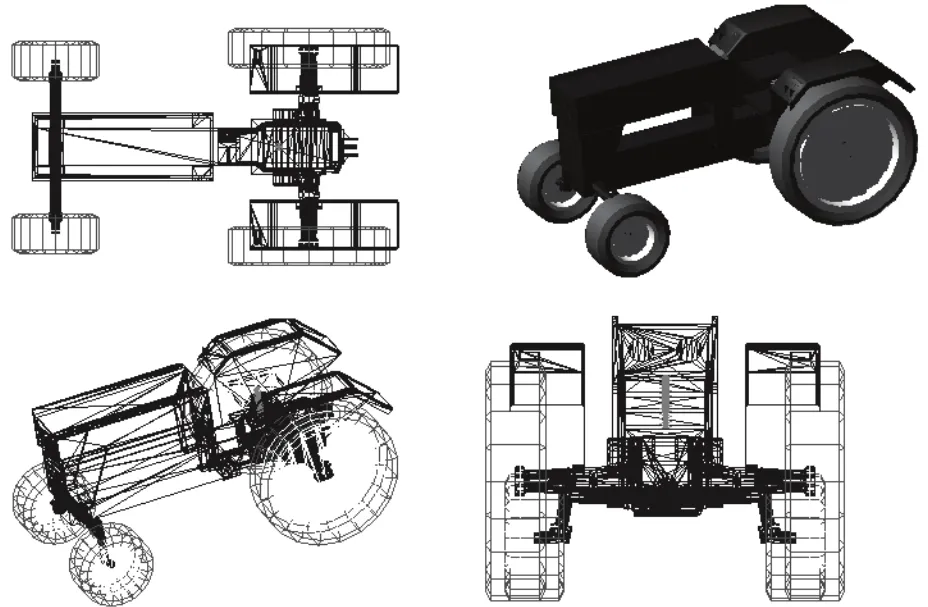
图3 JS-754拖拉机动力学整车模型Fig. 3 JS-754 tractor dynamics model

轮胎模型采用Fiala模型，并修改拖拉机前、后车轮参数（表2），Fiala轮胎模型具有一定的包容特性，包容特性对车辆垂直振动的研究有重大意义［21］。

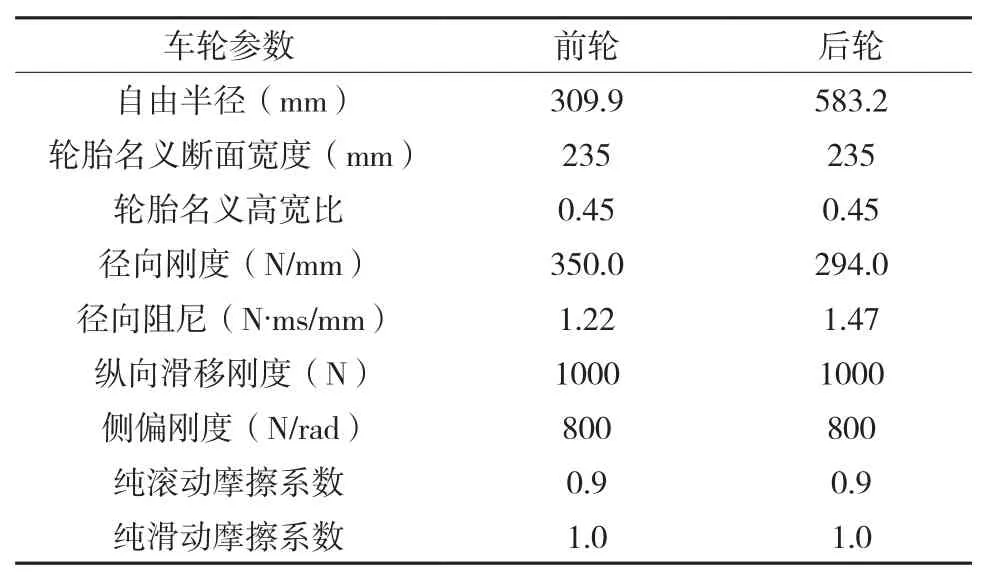
表2 拖拉机轮胎参数Table 2 The tire parameters of tractor

3 仿真结果与分析

3.1 JS-754拖拉机随机振动平顺性仿真结果与分析

仿真采用的是D级随机路面，根据座椅处垂直振动加速度（图4），计算加速度均方根值（aw）为0.390 9 m/s2，根据随机振动平顺性标准，因为0.32＜aw＜0.63，所以人的主观感受是有一些不舒适。由于拖拉机的振动特性比汽车较差，而且仿真的路面工况为较差的D级路面，该拖拉机振动较平缓，加速度均方根值较小，故该拖拉机的平顺性较好。

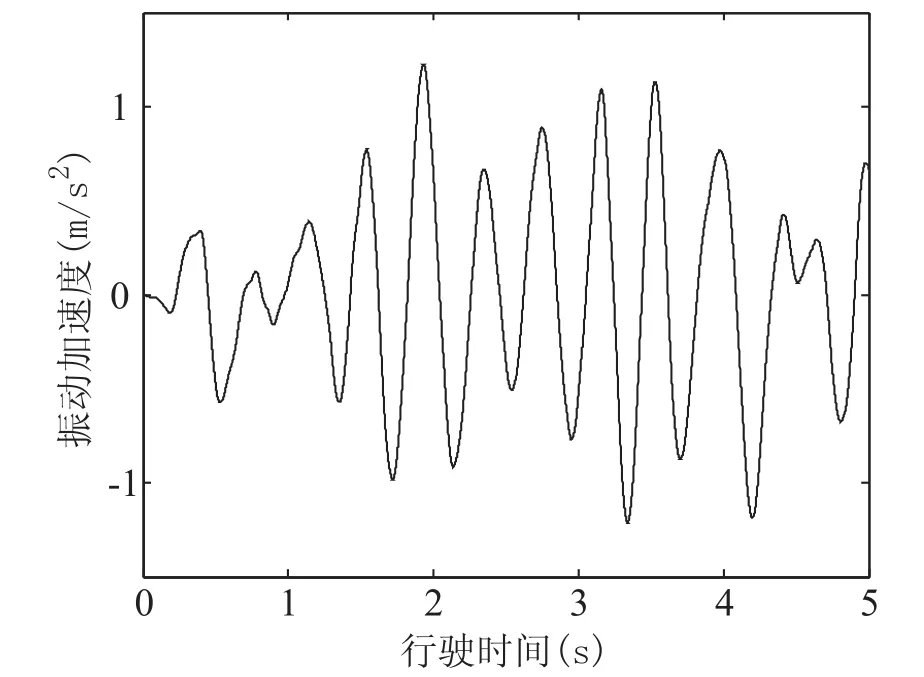
图4 座椅处垂直加速度振动曲线Fig. 4 Vertical vibration acceleration signal on the seat

拖拉机行驶过程中，胎压的变化范围306.2-375.2 kpa（图5），变化幅度约为69 kpa，根据方波平和朱自生［22］的研究，当大气温度在28-41 ℃范围内，平均车速在35-70 km/h范围内，轮胎气压的平均增量为96 kpa，现仿真车速为30 km/h，车速越慢，气压增幅越小，所以图5反映的轮胎气压变化在合理范围内。

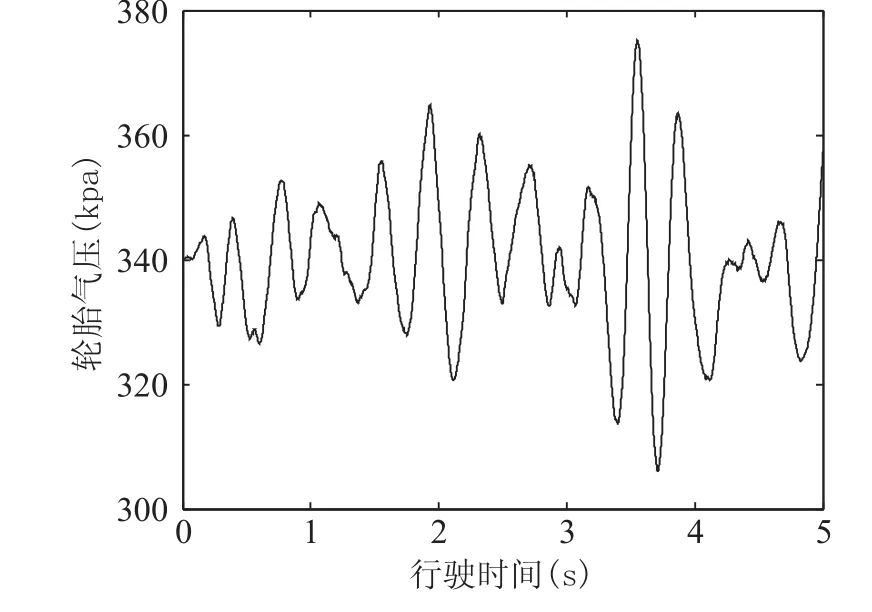
图5 拖拉机轮胎气压变化曲线Fig. 5 Signal of tire pressure

仿真结果表明，拖拉机前、后刚度特性的变化范围分别是408.8-442.4 kN/m和496.2-543.4 kN/m（图6）；前、后轮胎阻尼特性的变化范围分别是1 389-1 400 N·s/m和2 223-2 340 N·s/m（图7）。由于仿真时，前、后车轮受到相同动载荷的作用，所以胎压的变化相同，在合理的范围内胎压和刚度呈正相关，故前、后车轮的刚度变化较一致。由于拖拉机行驶时，后轮受到的路面激励较前轮滞后一段时间，而且不同轮胎的胎压和阻尼变化关系也不同，所以前、后车轮的阻尼变化差异较大。

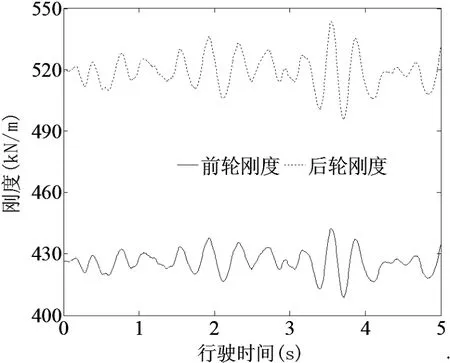
图6 拖拉机轮胎刚度特性变化曲线Fig. 6 Signal of tractor tire stiffness characteristics

3.2 JS-754拖拉机脉冲输入平顺性仿真结果与分析

根据GB/T 5902的标准，脉冲输入采用等腰三角形状的单凸块，对于拖拉机等非道路车辆三角形凸块的高度h=80 mm，长度L=400 mm。

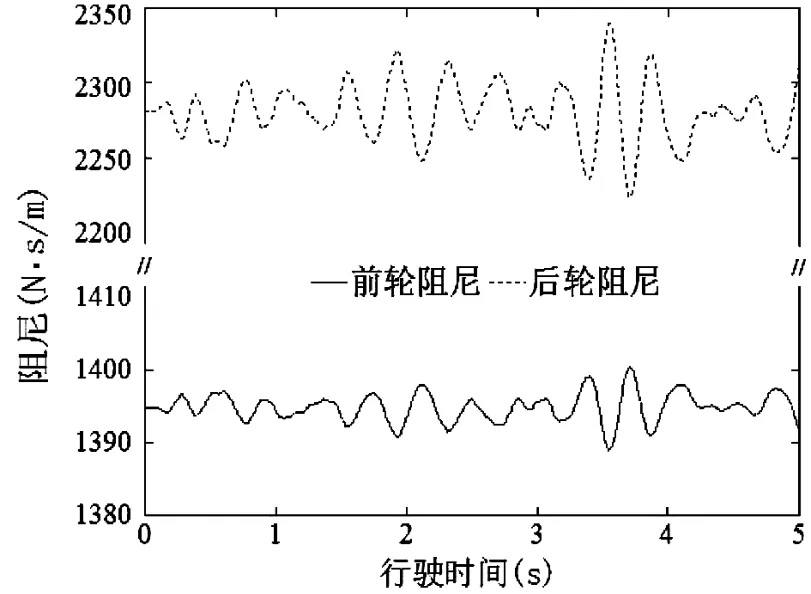
图7 拖拉机轮胎阻尼特性变化曲线Fig. 7 Signal of tractor tire damping characteristics

由于拖拉机等非道路车辆行驶速度的特殊性，为了更好的进行试验结果的比对，将车速的范围设为5、10、15、20和30 km/h，以拖拉机座椅垂直振动加速度的时间历程曲线（图8）和功率谱密度作为输出（图9）。

图8 拖拉机座椅处垂直振动加速度曲线Fig. 8 Vertical vibration acceleration signals of tractor seat

根据计算得到的脉冲输入评价指标值，各车速下座椅处最大垂直加速度（表3）皆小于34.59 m/s2，所以该拖拉机以正常行驶速度过凸块时对驾驶员的健康没有影响。

比较各车速下座椅处垂直振动加速度的时间历程曲线，可以明显看出加速度响应较大的波峰和波谷不只一处，这说明拖拉机受到的主要振动不只一次，Fiala轮胎模型与地面的相互作用方式是点接触，当前轮刚刚驶上三角形凸块时，由于速度的不断波动使得车速在垂直于座椅系统的方向上不断变化导致了座椅系统不再是相对于拖拉机的稳态而出现垂直方向的振动，当前轮驶下凸块时也是如此。前轮行驶完毕后，振动还未消除，而后轮又通过凸块导致新的振动产生，所以存在前后两次较大的振动且振动曲线的初期明显没有之后的振动幅度大。

由各车速垂直振动加速度功率谱密度图能看出，振动频率的范围在0-8 Hz以内，在3-5 Hz的范围内特别明显。当车速较小时，能看到有两个明显的波峰，还有一些较小的波，随着车速的增高，达到30 km/h时，两个较强波峰中的一个会明显减小，甚至在图上很难观察到，这说明，当车速较高时，前轮到后轮的间隔，前、后轮通过凸块的时间都会减小，从而使振动显得很集中。

图9 拖拉机座椅处垂直振动加速度PSD曲线Fig. 9 vertical vibration acceleration PSD curve of tractor seat

表3 脉冲输入平顺性仿真结果Table 3 Ride comfort simulation results with pulse input

座椅处垂直振动的最大值随着车速的上升而增大，增大的幅度是逐渐降低的。

4 结论

本研究提出了两种研究拖拉机振动的建模方法，并对拖拉机行驶平顺性进行综合评价，仿真得到了拖拉机在D级路面行驶时座椅处垂直振动加速度均方根值0.390 9 m/s2，脉冲激励输入时各车速的最大振动加速度都小于34.59 m/s2，JS-754拖拉机遇凸块不会对乘员的健康造成危害，表明了JS-754拖拉机的平顺性较好，对于农业车辆及非道路车辆振动特性的理论和实验研究，具有一定的参考价值。

拖拉机在随机振动的路面上行驶时，胎压变化幅度合理，约为69 kpa，前、后车轮的刚度变化差异较小，最大差异值约3.6 kpa，而阻尼变化的差异较大，最大差异值约106 N·s/m。JS-754拖拉机通过三角形凸块时，座椅处的振动主要为2次，振动初期的振幅小于中后期的振幅，振动集中在3-5 Hz的范围内，车速越快时，2次主要振动的间隔变短，振动更集中。

［1］ 鲁植雄. 农用汽车与拖拉机构造原理［M］. 北京： 北京理工大学出版社， 2000. Lu Z X. Agricultural Automobile and Tractor Structure Principle［M］. Beijing： Beijing Institute of Technology Press， 2000.

［2］ 徐刚， 朱思洪， 聂信天， 等. 国产拖拉机振动系统固有频率研究［J］. 振动与冲击， 2014， 33（15）： 157-161. Xu G， Zhu S H， Nie X T， et al. Natural frequencies calculation for vibrating systems of tractors made in China［J］. Journal of Vibration and Shock， 2014， 33（15）： 157-161.

［3］ 娄秀华， 毛恩荣. ADAMS在大马力拖拉机整机建模中的应用［J］. 农机化研究， 2008（9）： 187-189. Lou X H， Mao E R. Applications of adams in powerful tractors virtual prototyping［J］. Journal of Agricultural Mechanization Research， 2008（9）： 187-189.

［4］ 张广庆， 朱思洪， 宋庆德， 等. 基于ADAMS的铰接轮式重型拖拉机振动特性分析［J］. 机械设计， 2012， 29（6）： 61-65. Zhang G Q， Zhu S H， Song Q D， et al. Research on vibration characteristics of articulated wheel heavy tractor based on ADAMS［J］. Journal of Machine Design， 2012， 29（6）： 61-65.

［5］ Pearson P， Bevly D M. Modeling and validation of hitch loading effects on tractor yaw dynamics［J］. Journal of Terramechanics，2007， 40： 439-450.

［6］ Shahgoli G， Fielke J， Saunder C， et al. Simulation of the dynamic behaviour of a tractor-oscillating subsoiler system［J］. Biosystems Engineering， 2010， 106： 147-155.

［7］ Muzammil M， Siddiqui S S， Hasan F. Physiological effect of vibrations on tractor drivers under variable ploughing conditions［J］. Journal of Occupational Health， 2004， 46： 403-409.

［8］ 裘熙定， 季学武， 王志浩， 等. 轮胎刚度的非线性特性［J］. 吉林工业大学学报， 1994（4）： 9-15. Qiu X D， Ji X W， Wang Z H， et al. Study on non-Linear characteristics of tire stiffness［J］. Journal of Jilin University of Technology， 1994（4）： 9-15.

［9］ 谢俊淋， 张庆永. 基于Simulink的汽车平顺性仿真分析［J］. 机电技术， 2013（1）： 14-18. Xie J L， Zhang Q Y. Analysis and simulation of vehicle ride comfort based on Simulink［J］. Mechanical & Electrical Technology， 2013（1）： 14-18.

［10］ 余志生. 汽车理论［M］. 北京： 机械工业出版社， 2009. Yu Z S. The Theory of Automobile［M］. Beijing： China Machine Press， 2009.

［11］ 赵六奇， 刘锋. 参照国际标准ISO 2631的新草案修订汽车平顺性的评价方法［J］. 汽车工程， 1993， 15（6）： 371-377. Zhao L Q， Liu F. Revise the evaluation method of vehicles ride performance with reference to the new ISO 2631 draft［J］. Automotive Engineering， 1993， 15（6）： 371-377.

［12］ 高树新， 宫镇. 汽车脉冲输入平顺性评价指标限值的研究［J］.汽车技术， 1996（9）： 1-3， 7. Gao S X， Gong Z. Study on index limit of vehicle ride performance under pulse input［J］. Automobile Technology， 1996（9）： 1-3， 7.

［13］ 喻凡， 林逸. 汽车系统动力学［M］. 北京： 机械工业出版社，2005.Yu F， Lin Y. Vehicle System Dynamics［M］. Beijing： China Machine Press， 2005.

［14］ 谢伟东. 基于人椅系统三向振动的汽车平顺性建模与仿真［D］.杭州： 浙江工业大学， 2004. Xie W D. Dynamic modeling and simulation of vehicle ride comfort based on triaxial vibrations of person-chir system［D］. Hangzhou： Zhejiang University of Technology.

［15］ 王新忠， 于清泉， 胡文义， 等. 轮式拖拉机行驶振动力学模型及振动方程建立［J］. 黑龙江八一农垦大学学报， 1998， 10（1）：45-48. Wang X Z， Yu Q Q， Hu W Y， et al. The establishment of traveling vibration mechanics model and equation of vibration of wheeled tractors［J］. Journal of Heilongjiang Bayi Agricultural University，1998， 10（1）： 45-48.

［16］ 陆明万， 张雄. 从动能定理到第二类拉格朗日方程［J］. 力学与实践， 2003， 25（5）： 66-68. Lu M W， Zhang X. From the theorem of kinetic energy to the second Lagrange equation［J］. Mechanics in Engineering， 2003，25（5）： 66-68.

［17］ 刘任先. 拖拉机轮胎刚度和阻尼特性研究［J］. 农业机械学报，1988（2）： 17-24. Liu R X. Study of tractor tire stiffness and damping characteristics［J］. Transactions of the Chinese Society for Agricultural Machinery， 1988（2）： 17-24.

［18］ 聂信天， 史立新， 顾浩， 等. 农用轮胎径向刚度和阻尼系数试验研究［J］. 南京农业大学学报， 2011， 34（5）： 139-143. Nie X T， Shi L X， Gu H， et al. Research on the radial stiffness and damping of tractor coefficient tires through test［J］. Journal of Nanjing Agricultural University， 2011， 34（5）： 139-143.

［19］ 王泽鹏， 高峰， 薛风先. 轮胎气压与主要影响因素的关系试验［J］. 农业机械学报， 2007， 38（3）： 205-208. Wang Z P， Gao F， Xue F X. Test of the relationship between tire pressure and the main influence factors［J］. Transactions of the Chinese Society for Agricultural Machinery， 2007， 38（3）： 205-208.

［20］ 周一鸣. 拖拉机驾驶座位悬架系统的特性参数与驾驶员不同体重的最佳匹配［J］. 农业机械学报， 1983（4）： 27-43. Zhou Y M. The optimum matching of the characteristic parameters of tractor seat suspension system with the various weights of tractor-operators［J］. Transactions of the Chinese Society for Agricultural Machinery， 1983（4）： 27-43.

［21］ 郭孔辉， 刘青， 丁国锋. 轮胎包容特性分析及其在汽车振动系统建模中的应用［J］. 汽车工程， 1999， 21（2）： 65-71， 80. Guo K H， Liu Q， Ding G F. Analysis of tre enveloping properties and its application in modeling of vehicle vibration system［J］. Automotive Engineering， 1991， 21（2）： 65-71， 80.

［22］ 方波平， 朱自生. 轮胎行驶过程中温度及气压变化的试验研究［J］.轮胎工业， 1996， 16（5）： 302-306. Fang B P， Zhu Z S. Experimental study on temperature and pressure changes during the process of running［J］. Tire Industry，1996， 16（5）： 302-306.

（责任编辑：童成立）

Tractor modeling and its vibration analysis based on MATLAB/Simulink and ADAMS

CHENG Zhun， WANG Jun， LU Zhi-xiong
（College of Engineering， Nanjing Agricultural University， Nanjing， Jiangsu 210031， China）

Based on the theory and method of multi-body dynamics study， the mathematical and mechanical vibration model of JS-754 tractor was established using MATLAB and ADAMS software. The ride comfort of the tractor was simulated with the input signals of random vibration and pulse. The mathematical model consists of 3 degrees of freedom vibration model of tractor using the second equation of Lagrange. From the dynamic characteristics of the tire，a tractor vehicle tire coupling system was established. The mechanical model of JS-754 tractor was established by virtual prototyping technology， and the relationship between the various parts of the vehicle was defined. Simulation results showed that vertical Root-Mean-Square （RMS） acceleration was acquired which equals 0.390 9 m/s2on D grade road and the maximum response of the vertical vibrational acceleration velocity was less than 34.59 m/s2on the seat. The signal of tire characteristics with the tractor driving was obtained， the frequency range of vibration was concentrated between 3 and 5 Hz on the seat by simulation. The research shows that the ride comfort of JS-754 tractor is good. The proposed method of tractor vibration modeling is of great reference value， and it can provide the theoretical basis and modeling ideas for the research on the ride comfort of the tractor and other non-road vehicles.

tractor； multi-body dynamics； vibration； model； virtual prototype

National Natural Science Foundation of China （51175269）.

LU Zhi-xiong， E-mail： luzx@njau.edu.cn.

08 July， 2015； Accepted 19 October， 2015

S219.1； U462.3+3

A

1000-0275（2016）02-0395-07

10.13872/j.1000-0275.2015.0167

国家自然科学基金项目（51175269）。

程准（1992-），男，江苏苏州人，硕士生，主要从事车辆的动力学分析，车辆地面力学研究，Email： chengzhun38@163.com；

鲁植雄（1962-），男，湖北武穴人，教授，博士生导师，主要从事车辆地面力学研究，Email： luzx@njau.edu.cn。

2015-07-08，接受日期：2015-10-19