关于微积分极限思想的具体教学探讨

贺勤斌

（台州学院　数学与信息工程学院，浙江　临海　317000）

关于微积分极限思想的具体教学探讨

贺勤斌

（台州学院数学与信息工程学院，浙江临海317000）

极限理论是微积分的基础。极限概念在微积分中占有极其重要的地位和作用，该思想贯穿整个微积分的始终。微积分极限概念教学是非常重要的。学生对极限部分实质掌握，影响随后的其它概念和理论的掌握与理解。极限理论也是学生学习的一个难点，对该部分的教学探讨有助于学生掌握极限理论培养数学思维。

微积分；极限；导数

大学高等数学即微积分主要由二部分组成，即微分学和积分学。同时，微分部分也是积分部分的基础，而微分的核心思想就是极限理论。因此，极限在微积分中占有极其重要的地位和作用［1］。在大学数学教学中，新生一开始就会遇到极限的理论、定义。极限的定义有三种情况，即数列极限的ε-N定义、函数极限的ε-X定义和ε-δ定义。新生初次接触这些概念往往一头雾水，在学习以及教学上也造成一定压力。考虑到非数学专业学生只强调应用性、计算性，而不强调理论性，因此老师在极限的教学上就面临二种处理，一种处理是极限部分的教学一笔带过，而另一种处理就是花大量的时间认真仔细介绍该理论。而当今微积分教学中，大部分的教师处理该部分的方法就是第一种方法，即一笔带过。而该部分的教学是一笔带过，还是需要花时间认真介绍呢？这在教学上引起了一些讨论。结合本人多年的大学微积分教学经验，我认为对极限部分的理论教学应该认真讲解，而不该是一笔带过。我们知道数学是一门具有严谨逻辑性的科学，所有的知识都是环环相扣、紧密联系的，对该理论一笔带过的教学会对其后的一系列理论教学和学习造成大量的问题。

下面谈谈对极限部分的教学思想和方法。

1　历史介绍增加兴趣

极限的朴素思想和应用可追溯到古代哲学名著《庄子》中“截杖问题”以及我国3世纪的数学家刘徽创立的“割圆术”。在17世纪，由于科学与技术的发展促使数学家们研究变量的无穷小量。17世纪后半叶，牛顿和莱布尼茨在前人研究的基础上，分别独立地建立了微积分学，给出了极限的初步概念。虽然，当时微积分给数学界带来了革命性变化，在各个科学领域中得到广泛应用，但是由于当时不严谨的极限思想也引发了数学史上的第二次危机［2］。后来，19世纪由法国数学家柯西、德国数学家魏尔斯特拉斯等建立严密的极限理论，使得微积分这门学科才得以严密化［3-4］。

微积分作为一种数学工具，也是其它相应学科的基础，因此对于微积分的教学往往安排在新生的第一个学期。作为微积分的基础——极限的教学，就有必要详细深入介绍，使学生了解极限产生的历史、产生的原因以及极限思想的发展过程。在这一部分的教学可以适当增加一些数学史，培养学生的学习兴趣。

2　循序渐进引出定义

对于极限的教学要循序渐进，首先从数列的极限入手创建教学情境。例如，使学生通过直观观察数列的变化趋势：

很明显，同学们观察得出上述数列（1－4）当 n→∞时，分别有，这些结果是正确的。但是，绝大部分同学对数列（5）会得到不正确结果：.直观在数学的发展和创造中有着积极的角色，但数学绝对不能停留在直观的认识阶段。数学中仅凭直观甚至会得出危险的错误结论。必须指出数列（5）的极限为因此，也教育了学生必须认识到将凭借直观产生的定性描述转化为用规范化的数学语言表达数学问题的定量描述的重要性。通过上面的分析，从而也自然引出了数列极限的ε-N定义。

3　对比引导加深概念

数列 xn≈ ≈极限的ε-N定义有着准确的、完美的、精练的数学表达，即：Aε＞0，E N，当n＞N时，成立，则称数列 xn≈ ≈极限为a，记作

对于数列 xn≈ ≈极限有必要对于学生进行教学引导。比如，分析数列ε-N定义的原因与提法，引导学生自己对极限的理解，提出学生自己的极限定义，从而对比数列ε-N定义，找出不足，加深对数列ε-N定义的理解。

相对数列极限，由于函数f（x）的自变量有二种变化趋势，即x→∞和x→x0，所以函数的极限有两种情况，即ε-X定义和ε-δ定义。而函数ε-X定义完全类似于数列 xn≈ ≈极限，通过理解与对比学生自己完全可以得出该定义：，E X，当x＞X时，成立，，则称函数f（x）当x→+∞时的极限为A，记作.同时，也自然也得出x→-∞以及x→∞时的函数极限情况。因此，函数极限的教学顺序安排也是重要的，一个好的顺序安排就会使学生学习有一个自然过渡，更好掌握与理解相关概念。当然也适当解释给出函数另一种情况极限—函数ε-δ定义：当δ时，成立，则称函数f（x）当x→x0时的极限为A，记作

4　图解解释加深理解

图解数学学习法，可以从根本上提高学生的数学理解力，彻底搞清楚抽象的数学概念、定理和公式，让深奥的数学知识变得通俗易懂，唤起学生对数学的兴趣。在具体的极限教学过程，不论是数列极限的ε-N定义还是函数极限的ε-X定义和ε-δ定义，图解解释是必要的。

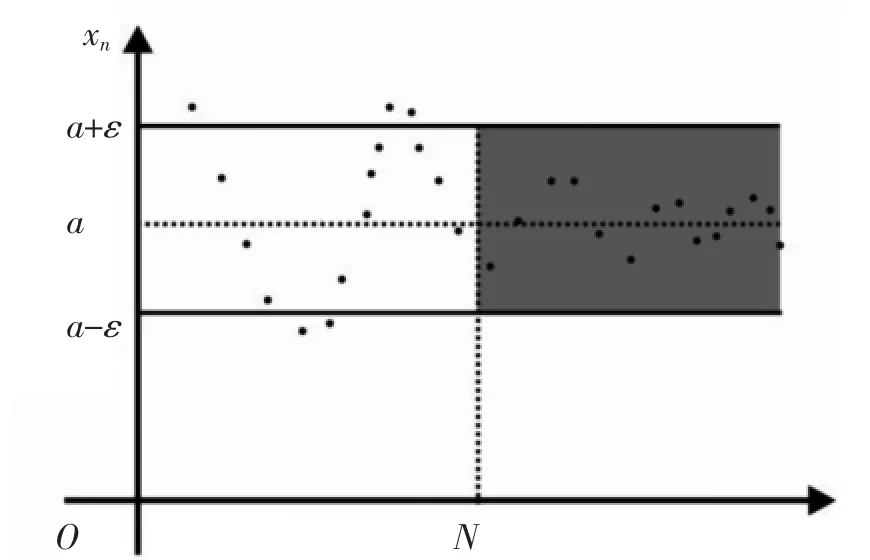
图1　数列极限的ε-N定义图解　

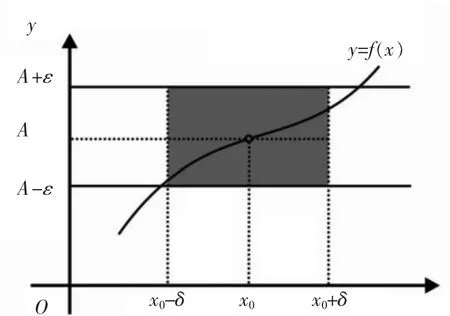
图2　函数极限的ε-δ定义图解

对于数列极限的ε-N定义可以用图1加以说明，指出该定义实质就是给定任意小的量ε，能不能找一个N，使得数列xn在N项之后全部落在图1的阴影带域中。对于函数ε-δ定义同样有必要图解分析，一方面详细解释x→x0时的函数变化趋势，说明函数极限与函数f（x）在x0的定义无关；另一方面解释该定义的实质是给定任意小的量ε，能不能找一个量δ（>0），使得在x0的去心邻域U（x0，δ）内f（x）图像全部落在图2的阴影带域中。

通过接合图解教学可以使学生完全掌握这种抽象的极限数学定义，从而为以后进一步深入学习微积分其它知识打下扎实基础。

5　总结

极限概念教学是非常重要的，一个好的开端会得到一个好的结果，而往往这个极限部分学生没有实质掌握，而影响随后的其它概念和理论的掌握与理解，使得学生的微积分学习变成了背公式解题目。微积分教学与学习绝对不是背公式。微积分的相关概念前后紧密联系、环环相扣的。只有从本质上理解掌握极限概念才能使学生对随后的其它知识有更进一步的理解，从而对微积分学习产生兴趣。

［1］王 庚．数学文化与数学教育［M］.北京：科学出版社，2004.

［2］霍华德·伊夫斯.数学史概论［M］.哈尔滨：哈尔滨工业大学出版社,2013.

［3］张国楚，徐本顺，王立冬，等.大学文科数学［M］.（2版）.北京：高等教育出版社，2007.

［4］同济大学数学系.高等数学［M］.（7版）.北京：高等教育出版社，2014.

［5］刘玉琏，傅沛仁．数学分析讲义［M］.（3版）.北京：高等教育出版社，1992.

Discussion on Lim it Thought in Calculus Teaching

HE Qinbin
（School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China）

Lim it theory is the basis of calculus.The concept of lim it thought has a very im portant position and role in the calculus,and the thought has always been penetrated throughout the calculus.It is very im portant of the lim it teaching in calculus.The virtual mastering of lim it theory w ill affect students to further understand other subsequent concepts and theories of calculus.The lim it theory is also a difficult point for students.The discussion on teaching lim it thought w ill help students to catch the lim it theory and develop mathematical thought.

calculus;lim it;derivative

10.13853/j.cnki.issn.1672-3708.2016.03.013

（责任编辑：耿继祥）

2015-12-13；

贺勤斌（1972－）,男,浙江台州人，副教授,研究方向:非线性动力系统。