钢筋混凝土材料参数对截面弯矩-曲率的影响研究

□文/喻志然

钢筋混凝土材料参数对截面弯矩-曲率的影响研究

□文/喻志然

对截面弯矩-曲率分析过程和涉及到的材料参数进行归纳总结并通过灵敏度分析得到改变取值对弯矩-曲率分析结果影响较大的材料参数，其中对等效屈服弯矩影响最大的是钢筋屈服强度，对等效屈服曲率影响较大的是钢筋屈服强度和钢筋的弹性模量；同时也分析了配筋率和轴压比对弯矩-曲率分析结果的影响，得到一些有用的结论，有利于设计者在弯矩-曲率分析中准确把握对结果影响较大的参数。

弯矩-曲率分析；等效；屈服弯矩；Mander模型；钢筋；混凝土

截面弯矩-曲率分析是延性抗震设计中的重要环节。弯矩-曲率分析得到截面弯矩与曲率关系的骨架曲线，该曲线与滞回规则共同决定结构在地震动作用下弯矩与曲率的对应变化关系，同时反应截面的抗弯能力及延性；因此准确的弯矩-曲率分析结果对结构延性抗震设计至关重要。由于弯矩-曲率分析中的材料参数繁多，把握对结果影响较大的参数并准确取值十分必要。通过对典型钢筋混凝土桥墩截面的分析，对影响弯矩-曲率分析的材料参数进行研究。

1　材料参数

弯矩-曲率分析需要将截面划分为若干个纤维块，见图1。在平截面假定的基础上建立截面各个纤维块的应变ε与截面曲率φ的关系；然后根据材料的“应力-应变”关系建立纤维块应力与截面曲率的关系；通过各个纤维块应力的叠加与截面所受轴力、弯矩建立平衡方程，从而求解轴力一定时，截面曲率φ与弯矩的关系。在得到截面弯矩-曲率关系曲线后，为计算方便需要将该曲线等效为较为简单的理想弯矩-曲率曲线，文献［1］规定理想弯矩-曲率曲线通过受拉钢筋首次屈服点并保证图2阴影部分面积相同，得到理想双折线弯矩-曲率曲线，共包含等效屈服弯矩My、等效屈服曲率φy和极限曲率φu3个参数。

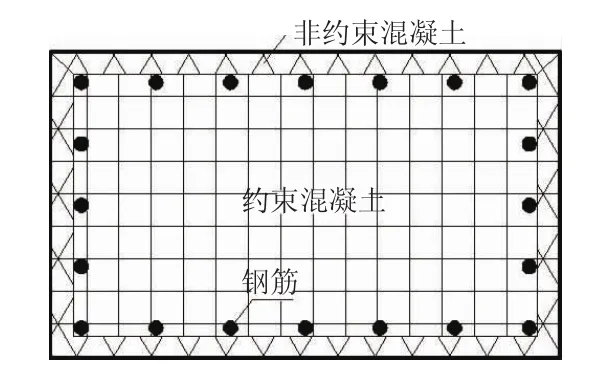
图1　钢筋混凝土截面纤维划分

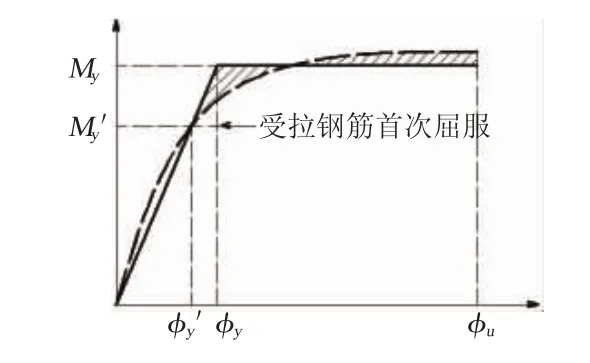
图2　截面等效弯矩-曲率曲线

弯矩-曲率分析中最主要的是截面中材料的本构关系，即“应力-应变”关系。目前，常用的混凝土“应力-应变”关系为Mander模型，见图3。

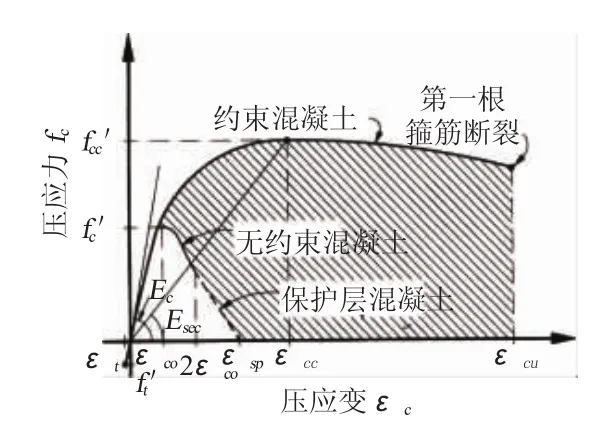
图3　Mander混凝土应力-应变曲线

Mander给出了约束混凝土应力-应变关系的解析表达式为

式中：fcc＇为约束混凝土峰值压应力，文献［2］对圆形截面和矩形截面分别给出了具体计算方法。

式中：εc为混凝土压应变；εcc为约束混凝土峰值压应变，按式（3）计算。

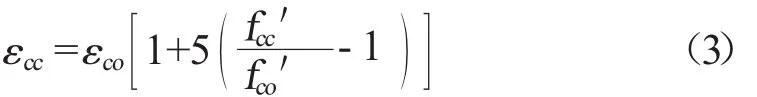
式中：εco为无约束混凝土峰值压应变，文献［2］取εco=0.002；fco＇为无约束混凝土峰值压应力。

式中：Ec为混凝土弹性模量（切线弹性模量）；Esec为约束混凝土割线模量，Esec=fcc＇/εcc。

文献［1］第7.3.9条规定了约束混凝土极限压应变εcu的计算方法。

为了定义无约束混凝土应力-应变关系，文献［2］假定当混凝土应变εc＞2εco时，无约束混凝土的压应力线性降到零，混凝土压应力为零时其应变达到压溃应变εsp，文献［2］取εsp=0.006。

钢筋应力-应变关系采用双折线，不考虑应力强化。钢筋需要确定的参数：屈服强度fy、弹性模量Es。钢筋极限应变按文献［1］规定取0.1。

总结截面弯矩-曲率分析需要确定的材料参数：无约束混凝土的峰值压应力fco＇、切线弹性模量Ec、约束混凝土的峰值压应力fcc＇、极限压应变εcu、切线弹性模量Ec（与无约束混凝土相同）、纵筋的屈服强度fy、弹性模量Es。

2　参数灵敏度分析

为研究上述6个参数对截面等效屈服弯矩、等效屈服曲率及极限曲率的影响程度，借鉴“龙卷风图（Tornadodiagrams）”分析方法的思想进行灵敏度分析。

“龙卷风图”分析方法［3］属于局部灵敏度分析，其特点是只针对一个参数，对其他参数取其中心值或平均值，评价模型结果在该参数每次发生变化时的变化量。参数的变换方法可分为两种：

1）因子变化法，如将预分析的参数增加10%或减少10%；

2）偏差变化法，如将预分析的参数增加一个标准差或减少一个标准差。

选取2.8 m×1.5 m矩形桥墩截面，混凝土强度等级C40，截面纵筋和箍筋均采用HRB400级钢筋。纵筋直径32 mm，配筋率1.531 9%；箍筋直径14 mm，箍筋间距100 mm，长度方向配箍率0.589 4%，宽度方向配箍率0.404 6%。建立截面纤维模型见图4，轴力2 000 kN。根据截面的材料等级及配筋率得到影响截面弯矩-曲率曲线的6个参数计算点的取值并将每个参数分别增加、减小10%，见表1。

图4　截面钢筋布置及纤维单元划分

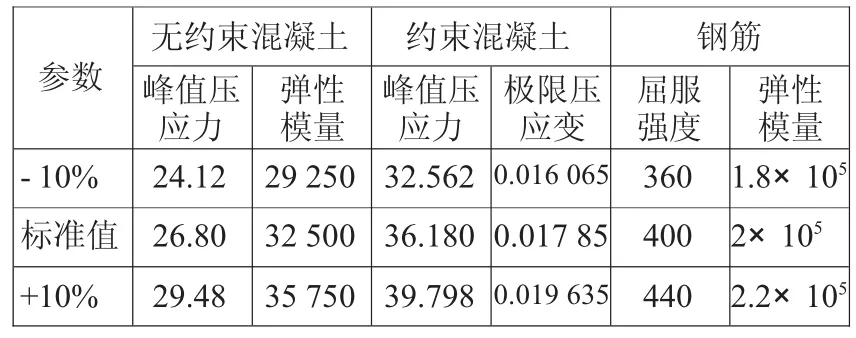
表1　参数计算点取值MPa

分别对每个参数对应取表1值，其他参数取标准值，轴力2 000 kN，计算得到宽度方向等效屈服弯矩My、等效屈服曲率φy和极限曲率φu见表2-表4。

表2　各参数计算点对应的等效屈服弯矩值kN·m

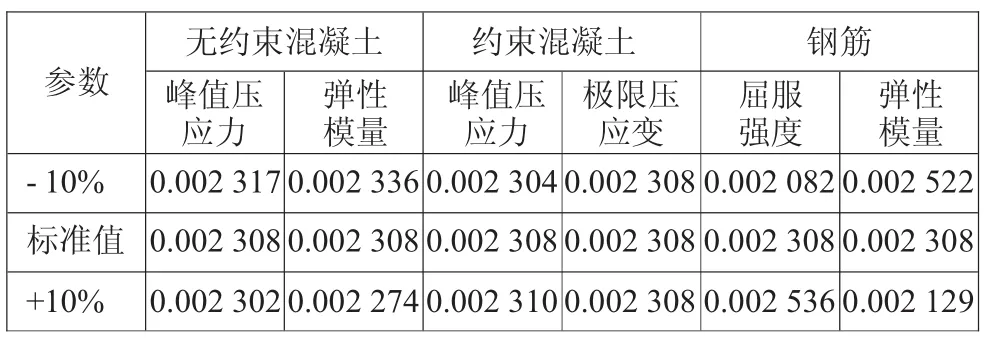
表3　各参数计算点对应的等效屈服曲率m-1

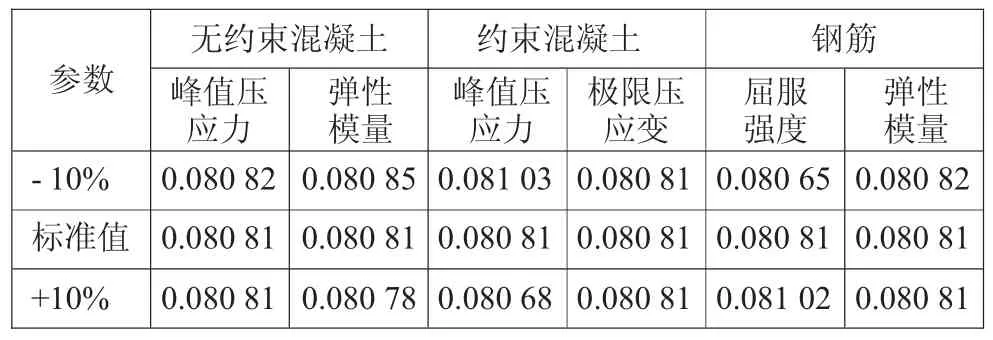
表4　各参数计算点对应的极限曲率m-1

对以上各参数的计算结果按整体平均值进行归一化处理，见表5-表7。

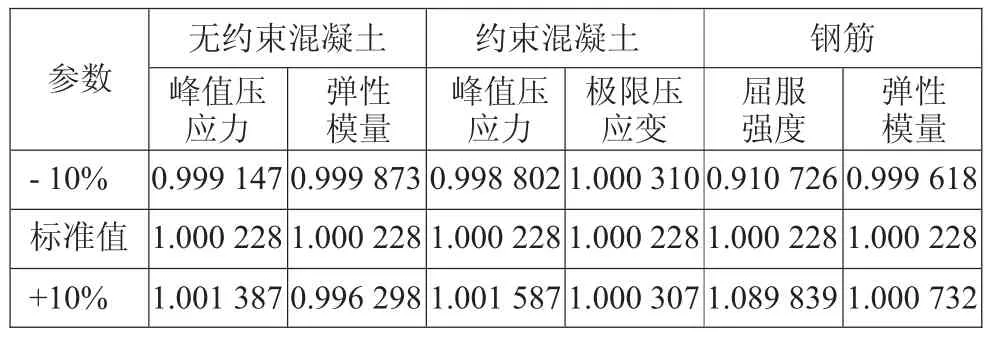
表5　各参数计算点对应的等效屈服弯矩值（归一化）

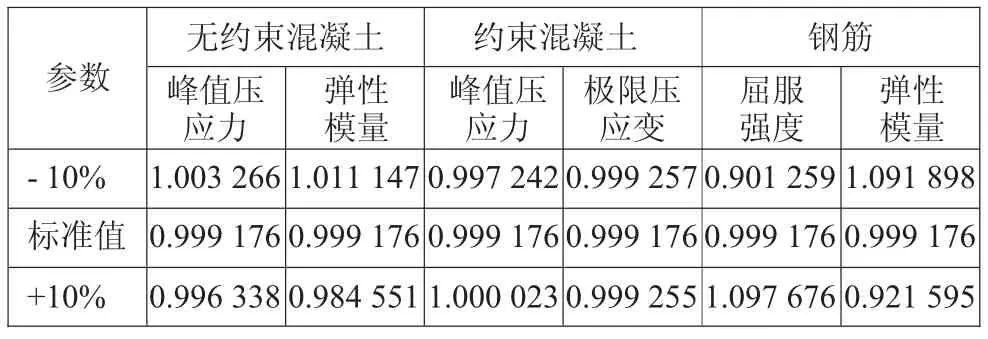
表6　各参数计算点对应的等效屈服曲率（归一化）

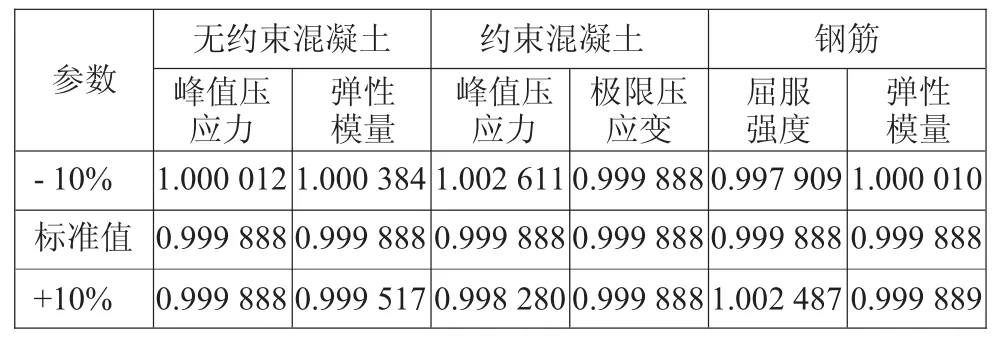
表7　各参数计算点对应的极限曲率（归一化）

由上述计算结果可得，参数变化±10%对等效屈服弯矩影响最大的是钢筋屈服强度，对于本算例其对结果的影响程度为-8.9274%～8.9839%；其他参数变化±10%对等效屈服弯矩影响均不大。参数变化±10%对等效屈服曲率影响最大的也是钢筋屈服强度，对于本算例其对结果的影响程度为-9.874 1%～9.767 6%；其次为钢筋弹性模量，对结果的影响程度为-7.840 5%～9.189 8%。各参数变化±10%对极限曲率的影响均不大，分析其原因是由于本算例决定极限曲率（即计算终止点）的是钢筋极限应变0.1，在此之前约束混凝土还未达到极限压应变，对于约束混凝土先于钢筋达到极限压应变的情况，约束混凝土的极限压应变必然影响截面的极限曲率。

3　配筋率的影响

前文算例截面的配筋率为1.531 9%，本节通过改变纵筋直径，不改变纵筋布置方式的方法改变截面配筋率为0.598 4%，减小60.94%。以表1中各参数的标准值进行计算，比较两种配筋率截面的计算结果见表8。

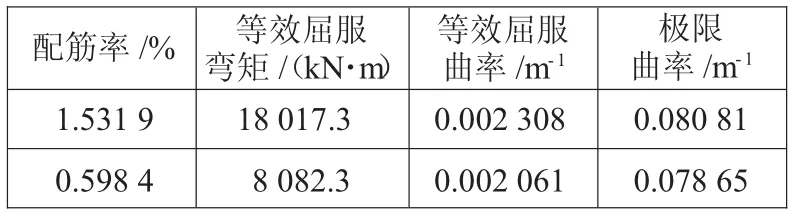
表8　配筋率对弯矩-曲率的影响

由表8可得，配筋率的变化对等效屈服弯矩的影响最大，其影响程度与纵筋屈服强度对等效屈服强度的影响程度相当。配筋率对等效屈服曲率和极限曲率的影响相对较小。

4　轴压比的影响

将轴力改为1 000 kN，对应的轴压比0.008 884，取配筋率取0.598 4%。以表1中各参数的标准值进行计算，比较两种配筋率截面的计算结果见表9。

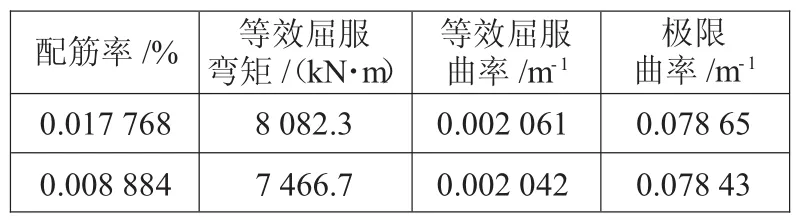
表9　配筋率对弯矩-曲率的影响

由表9可得，轴压比的变化对等效屈服弯矩的影响最大，但其影响程度与纵筋屈服强度、配筋率对等效屈服强度的影响程度相比较小。

5　结论

1）参数变化±10%对等效屈服弯矩影响最大的是钢筋屈服强度，本算例其对结果的影响程度为-8.927 4%～8.983 9%。

2）参数变化±10%对等效屈服曲率影响最大的是钢筋屈服强度，本算例其对结果的影响程度为-9.874 1%～9.767 6%；其次为钢筋弹性模量，对结果的影响程度为-7.840 5%～9.189 8%。

3）各参数变化±10%对极限曲率的影响均不大，这是由于本算例决定极限曲率（即计算终止点）的是钢筋极限应变0.1，在此之前约束混凝土还未达到极限压应变，对于约束混凝土先于钢筋达到极限压应变的情况，约束混凝土的极限压应变必然影响截面的极限曲率。

4）配筋率的变化对等效屈服弯矩的影响较大，其影响程度与纵筋屈服强度对等效屈服强度的影响程度相当。配筋率对等效屈服曲率和极限曲率的影响相对较小。轴压比的变化对等效屈服弯矩有一定影响，但其影响程度与纵筋屈服强度、配筋率对等效屈服强度的影响程度相比较小。

［1］CJJ 166—2011，城市桥梁抗震设计规范［S］.

［2］Mander J B，Priestley MJ N，Park R.Theoretical Stress-Strain Model for Confined Concrete［J］.ASCE Journal of Structural Engineering，1988，114（8）：1804-1826.

［3］Raychowdhury P.Nonlinear Winkler-based Shallow Foundation Model for Performance Assessment ofSeismicallyLoaded Structures［D］.San Diego：UniversityofCalifornia，2008.

U442.5

C

1008-3197（2016）03-55-03

2016-03-03

喻志然/男，1989年出生，助理工程师，天津市市政工程设计研究院，主要从事道桥设计工作。

□DOI编码：10.3969/j.issn.1008-3197.2016.03.018