ICP-AES法测定外科植入物用钛合金TC4 ELI中钒的不确定度评定

北京市医疗器械检验所（101111）王利霞 吴晓丽 黄永富 岳卫华 崔永平

当前用于制造外科植入物和矫形器械的医用金属材料主要有不锈钢、钴基合金和钛基合金三大系列。其中钛及钛合金由于比强度高、生物相容性好、耐蚀性好等特点，被广泛地应用于在各类植入产品中。TC4 ELI是近年来在Ti-6Al-4V基础上改进的新型钛合金材料，该合金在原Ti-6Al-4V的基础上，降低了氧等间隙元素的含量，其力学性能与Ti-6Al-4V相当，但提高了合金的断裂韧性，使植入物在人体内承受较为复杂应力并且受到强烈冲击力等情况下不易断裂。TC4 ELI合金中的铝和钒的含量是决定TC4 ELI钛合金性能的关键指标，准确测定这两个元素的含量对这类合金的质量控制有重要的意义。测定铝、钒元素含量的经典检测方法是传统的化学分析方法，包括容量法、光度法[1][2][3]。传统的化学分析方法由于操作复杂、步骤多，容易引入人为操作误差，现已较少使用。电感耦合等离子发射光谱法由于具备可同时测定多种元素、检出限低、精密度好、准确度高、线性范围宽、分析速度快等优点，成为目前用于钛及钛合金中铝、钒元素含量测试主流的仪器分析方法[4]。本文依据JJF 1059-1999《测量不确定度评定与表示》，对ICP-OES法测定TC4 ELI中的钒含量进行不确定度的分析，找出影响检测准确性的因素，确定测量结果的可信度，为该方法在外科植入物用钛合金TC4 ELI的质量安全评价的应用提供科学依据。

1 实验部分

1.1 仪器与试剂 iCPA 6300系列电感耦合等离子体发射光谱仪（美国Thermo Fishier）；梅特勒-托利多公司XP205DR电子天平；高纯金属钛：纯度大于99.99%；V标准溶液：质量浓度为1000μg/mL，国家有色金属及电子材料分析测试中心；硝酸、盐酸：优级纯，北京化学试剂厂；氢氟酸：优级纯，阿拉丁试剂（上海）有限公司。试验用水：Milli-Q纯水机制备的超纯水。

I C P-A E S 工 作 条 件 为：R F 功 率1150W；垂直观测高度12cm；蠕动泵转速50rpm；雾化器气体流量0.60L/min，辅助气流量0.5L/min；测量2次；样品冲洗20s；最大积分时间：长波范围10s，短波范围5s。

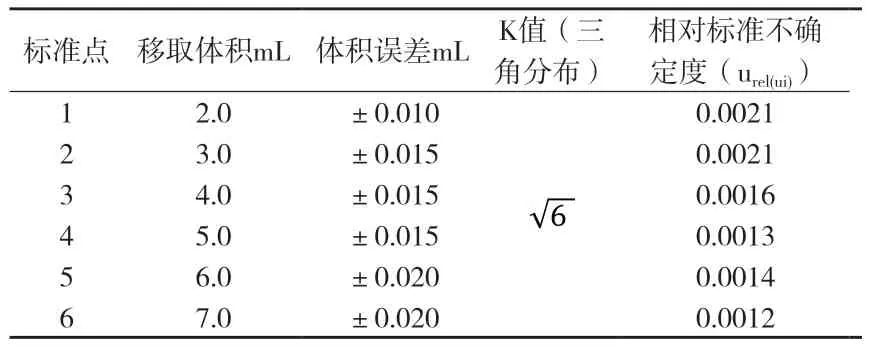
附表1 各标准点移取体积相对标准不确定度

附表2 建立标准曲线的标准溶液的质量浓度与相应的光谱强度

附表3 重复性实验产生的相对标准不确定度

附表4 各个相对标准不确定度分量的来源和数值

1.2 实验步骤 样品溶液的制备：称取0.1g样品置于250mL聚四氟乙烯烧杯中，加少量水，加入HCl+HNO3（2+1）5mL，缓慢滴加2mL的HF直至试样完全溶解，转移至100mL塑料容量瓶，用超纯水定容。

标准溶液的制备：称取纯钛6份，每份0.1g，分别置于250mL聚四氟乙烯烧杯中，加入HCl+HNO3（2+1）5mL，缓慢滴加2mL的HF直至试样完全溶解，转移至100mL塑料容量瓶，用分度吸量管分别加入3.0、4.0、5.0、6.0、7.0、8.0mL浓度为1000μg/mL的V标准溶液，用超纯水定容，混匀。

2 不确定度评定过程与结果

2.1 建立数学模型 实验原理：样品在聚四氟乙烯烧杯中，用合适比例的盐酸、硝酸、氢氟酸消解后，转移至塑料容量瓶定容。将溶液引入ICP-AES，测量钒的分析线发光强度，根据钒的分析线强度与含量成正比的关系，自动计算出钒的百分含量。

待测元素质量分数的数学模型为：

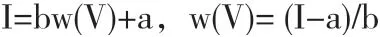
式中：I为仪器测得的光谱吸收强度，b，a分别为标样标准化曲线的斜率和截距。

按此数学模型对试样中V元素含量进行测定。首先标准化得到标准曲线，然后对试样溶液进行测定，得到V元素的含量值。

2.2 各标准不确定度分量的来源分析 根据数学模型及测定实验步骤，该测定方法中不确定度的来源主要为：①标准溶液配制过程中产生的不确定度，该分量不确定度来自于所用待测元素标准溶液储备液的不确定度，标准溶液配制定容过程；②试样前处理过程中产生的不确定度，产生该分量不确定度的实验步骤为天平称取试样，试样溶液的定容；③仪器分析测定过程中产生的不确定度，标准曲线拟合，试样重复测定。

2.3 各标准不确定度分量的评定

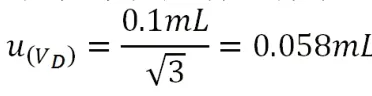
定容时，容量瓶和溶液的温度与校正时的温度不同引起的体积不确定度（实验温度为20±2℃，水的体积膨胀系数为2.1×10-4℃-1）为：

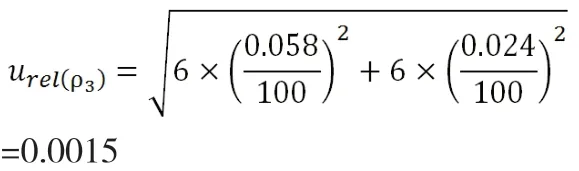
综上所述，在标准溶液配制过程中产生的相对标准不确定度为：

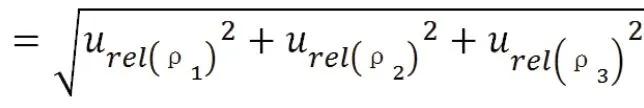
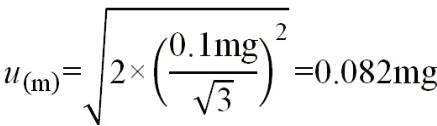
实际试样的称样量为100.0mg，则相对标准不确定度为：

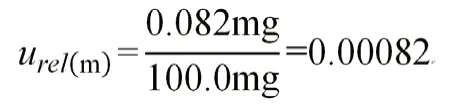
定容时，容量瓶和溶液的温度与校正时的温度不同引起的体积不确定度（实验温度为20±2℃，水的体积膨胀系数为2.1×10-4℃-1）为：

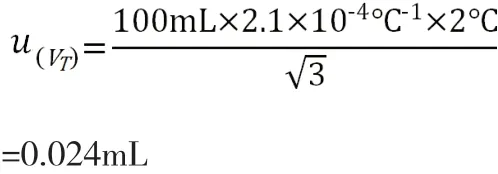
2.3.3 仪器分析测定过程中产生的不确定度。

2.3.3.1 标准系列溶液校准曲线拟合引入的相对标准不确定度如附表2所示。拟合出的校准曲线回归方程为：I=bw(V)+a =43906.5 w(V)+2026.4；r =0.9999。由标准溶液校准曲线拟合引入的标准不确定度计算公式为：

式中：s-校准曲线的标准差

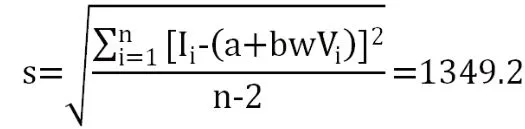
式中： b 为校准曲线的斜率，b=43906.5；P为试样溶液平行测定次数，P=6；N为校准过程中标准溶液测量的总次数，每个标准溶液测3次，N=18；W(V)为试样中实际测得的试样中V的含量，W(V)= 4.00%；标准溶液中V元素含量的平均值； W(Vi)为各标准溶液中V的含量；计算可得=0.015%；相对标准不确定度：

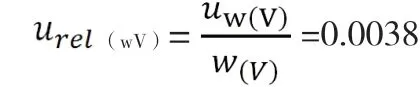
重复性实验产生的相对标准不确定度，对试样平行测试6次，结果见附表3。

重复性实验产生的标准不确定度

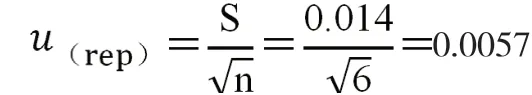
相对标准不确定度为：

2.4 合成标准不确定度和扩展标准不确定度的计算 各相对标准不确定度分量的来源和数值如附表4所示。由附表4数据计算，则合成相对标准不确定度为：计算得到相对合标准不确定度为0.0059。合成标准不确定度=4.00% 0.0059=0.024%，取包含因子为2，则扩展不确定度为=0.024%×2=0.048%，试样中V元素含量为 wAl=4.00%±0.048%，K=2。

3 结论

本文对ICP-AES法测定外科植入物用钛合金TC4 ELI中钒元素含量进行了不确定度评定，钒含量的拓展不确定度为0.048%。从不确定度评定过程可以看出，标准溶液配制和校准曲线的拟合对测量不确定度的贡献最大；除了标准溶液配制过程引入的误差外，仪器本身在测定常量元素时的不稳定性对测试结果也会造成影响。因此，在测试前需要严格优化仪器状态，使检测时的波动性控制在可接受范围内，同时严格控制系列标准溶液的配制过程，建立合理的工作曲线范围，保证样品检测结果的准确度和可信度。此外，不确定度是不断变化的，随测定过程涉及的仪器、试剂、标准物质、测试人员等因素的变化，实验室积累的数据也会有变化，不确定度也会相应发生变化。实验室要结合实际测试工作，不断积累测试数据，不断更新测定方法的不确定度，这样得到的不确定度才更可信合理。