基于贝叶斯网络的HPPP 基础设施项目特许期的分析方法研究

宋志凯，马金平，郭笑月

（青岛大学 商学院，山东 青岛 266071，E-mail：songzhikai74224@163.com）

基于贝叶斯网络的HPPP 基础设施项目特许期的分析方法研究

宋志凯，马金平，郭笑月

（青岛大学 商学院，山东 青岛 266071，E-mail：songzhikai74224@163.com）

合理确定 PPP项目的特许期一直是政府和社会投资者关注的核心问题，其中分析各种不确定因素如何对特许期产生影响又是解决这个问题的关键。为研究HPPP项目运营期中收支不确定因素及其关系对项目特许期时间跨度的影响，同时兼顾项目可行性评估标准的要求，将贝叶斯网络和净现值法相结合，提出了基于贝叶斯网络的HPPP项目特许期分析方法。在此基础上，对项目生命周期进行区间划分，并对最大概率组合进行折现分析，以确定HPPP项目特许期的可能区间范围。通过对实例验证了该方法的可行性，同时为指导实践工作提供了参考。

混合融资；PPP项目；贝叶斯网络；特许期

基础设施建设项目，尤其是大型交通项目，通常具有投资规模较大，投资回收期较长，投资收益不确定的特点。近几年，我国虽然采用混合 PPP （Hybird Public Private Partnership，HPPP）模式取得一些成功案例，但就实际情况而言，由于风险估计不足，并未达到预期效果。尽管各级政府颁布了多项激励政策[1]，但大多数投资者仍持有观望状态，原因在于项目诸多不确定性因素的存在，这些因素直接影响企业的预期净收益。此外，PPP项目较长的运营期跨度使得项目实施的可预测性降低，且学术界关于项目特许期的研究也较少关注不确定因素之间的相关关系。

确定合理的特许期是PPP项目协议的一个核心问题，近年来，许多学者都采用不同的视角和方法进行探究。其中，大多数采用现金流量净现值法（NPV）来确定PPP项目特许期，如Hanaoka等[2]将项目净现金流量现值作为衡量项目可行性的标准，计算出对公共部门和私人部门都有利的项目特许经营期，从而更好地保护私人部门的利益；王东波等[3]通过文献回顾和分析，构建项目收入和项目成本概率分布函数并进行项目区间模拟，然后根据NPVR的累计概率确定最终的特许经营期。

有学者从动态博弈的角度研究政府部门和项目公司之间的PPP项目特许期决策问题，采用实物期权和博弈论相结合的方法进行分析。如刘伟等[4]以投资双方项目价值最大化为决策目标，根据期权博弈理论构建完全信息动态博弈模型，以确定政府部门和私人部门的最优投资时机并求解 BOT项目特许期的可行区间；张俊生等[5]基于实物期权理论建立项目分期的期权博弈模型，从而有效地保护政府利益并提高项目建设的质量，并增加各参与方管理的能动性和灵活性。

PPP项目实施过程中诸多不确定性因素的存在，增加了项目特许期确定的难度。为了更加准确的模拟市场运作，有的学者引入Monte Carlo方法，并结合模糊数学、系统动力学模型等进行优化仿真。如 Carbonara等[6]在满足投资双方最低收益和风险公平分配的前提下，运用Monte Carlo方法模拟分析不确定条件下PPP项目的最佳特许期经营时点，此点同时满足合作双方风险承受能力许可前提下的净现值差额最小；Thomas等[7]将收费制度等因素作为确定性变量，将运营期收支作为不确定参数，利用Monte Carlo方法建立仿真模型，同时引入公共参与者不同的内含报酬率来反映特许经营商可以接受的不同收益率，以此来分析特许经营期的最优实现条件。

贝叶斯网络（Bayesian Network，BN）是基于先验信息进行概率推理的图形化表述，它可以从概率的角度分析不确定性变量之间条件相关产生的因果关系，被广泛应用于软件维护、数据挖掘、医疗诊断、国防系统等领域，并开始向项目管理领域延伸。如周亮等[8]引入工作节点和时间节点，建立改进的工程项目进度BN模型，对项目工作和持续时间的不确定关系进行研究分析，证明了BN在分析工程项目进度风险管理中的有效性；Vahid等[9]结合贝叶斯网络的推理过程对成本项目之间的相关性和因果关系建立定量评估框架，进行模拟分析，为项目管理的复杂性提供合理解释。

上述研究较少关注变量的不确定性变化，而且只考虑了自变量和因变量之间的因果关系，并未考虑自变量之间的相关关系以及这种相关关系对因变量的影响。对于一个PPP项目而言，其建设期较短，运营期较长，期间存在诸多影响项目运营期的不确定因素，特别是在经济环境“动荡”的新常态下，许多收支因素本身就是不确定变量，作为研究变量不确定性以及不确定性关系的方法，贝叶斯网络可以很好地解决上述问题。

1　HPPP基础设施项目特许期的概念界定和影响因素分析

混合融资模式下PPP项目特许期是指从项目建设期开始至移交政府部门前，允许私人部门通过向基础设施使用者收取合理费用来收回成本的一个最低经营管理期限，即同时包括项目建设期和项目运营期[10]。如图1所示。

图1　混合PPP项目特许期概念界定

鉴于PPP项目寿命或特许运营期较长的特点，运营过程中的一些不确定因素和风险问题，都会对PPP项目特许期区间的确定产生重要影响。在合理确定HPPP项目特许期的过程中，必须充分考虑各方面因素，如建设期投资成本、收费标准、投资回报率、利润分成等。其中，建设期投资成本是项目建设的资金投入数额，也是确定特许经营期的最低回收标准；收费标准的高低与消费者的使用偏好和运营期的现金流入相关，直接决定项目特许经营期的时间跨度；投资回报率是对项目未来现金净流量进行现值估计的折现比率，是政府允许社会资本进行投资的合理收益率。除此之外，PPP项目特许期也会受到合作双方利润分配比例的影响，如果任何一方没有通过分享收益来弥补成本支出都会要求相应延长运营期限。

对于基础设施项目而言，与公共部门致力于效用最大化相比，社会资本更倾向于利益最大化，即在风险可控范围内追求项目投资带来的净现金流量最大。从长期来看，经济环境的复杂性迫使材料、人工等成本因素呈现不确定变化，从而引起项目现金流的收支变动。公路PPP项目建设期以及初始投资成本可以基本确定，收费标准可参考类似公路项目制定。另外，项目计算采用的投资回报率或折现率应当根据项目实施所处的经济环境决定，在一定时期内不会发生较大波动，可以引用短期国债利率或同期银行贷款利率。

2　HPPP基础设施项目CBN的建模

2.1HPPP项目特许期CBN的定义

贝叶斯网络是在变量先验信息的基础上，利用有向无循环图进行不确定变量间关系描述和推理的概率图模型。基础设施建设HPPP项目特许期贝叶斯网络则是利用贝叶斯网络对HPPP运营期成本项目和收入项目不确定性关系进行逻辑推理的图形化网络，简称特许期贝叶斯网络（Concession Bayesian Network，CBN）。贝叶斯网络G=BN（V，L）满足以下条件时，才能称之为基于净现值法的特许期贝叶斯网络：

（1）V={Ri，Ci，r}，其中变量Ri表示一系列项目收入所对应的节点集合，Ci表示一系列项目成本所对应的节点集合，r为项目投资回报率。

（2）L={LRR，LCC，LRC}描述各变量之间的因果关系，其中 LRR表示项目收入之间的关系，LCC表示项目成本之间的关系，LRC表示项目收入与项目成本之间的关系。

（3）每一个变量离散取值范围有限，每个节点的子集Xi（i=1，…，n）和它的父节点集Πi，都对应一个概率分布且满足，其中πi是Πi的配置。

（4）影响项目收入R和项目成本C的变量及其他风险因素，本身存在不确定性，且对HPPP项目特许期的确定存在条件相关关系。

（5）项目投资建设区分双方投资比例，且投入和产出以付现资产为主，不考虑非付现资产，将NPV作为判断HPPP项目可行性的标准。

贝叶斯网络模型中的参数/变量有三类，包括取固定值的常量、通过概率分布描述的随机部分及通过数学定义刻画变量之间关系的逻辑部分。在一个HPPP项目环境下，运营期较长，通常可不考虑项目移交政府的后期运营部分。根据上面对HPPP基础设施建设项目特许期的影响因素分析，参数选择如表1所示。

表1　HPPP项目CBN模型参数选择

2.2HPPP项目CBN的网络拓扑结构

贝叶斯网络通常采用网络图形表示，包含一系列节点和箭头。其中，节点表示HPPP项目特许期贝叶斯网络中的随机变量；任意两个节点之间的箭头或有向边，表示两个变量之间的直接依赖关系。模型构建过程中随机变量之间是否存在相关关系，取决于生产实践过程。贝叶斯网络中变量之间的 3种相关关系如图2所示。

图2　CBN中的不确定关系

在实际应用中，通常根据因果关系来构建贝叶斯网络结构，通常包括多个分连和汇连关系，根据因果机制独立假设，不同的原因变量对结果变量的影响是独立的，且总影响是根据各变量按其单独影响的贡献概率进行算子合成。由此，根据HPPP项目特许经营期的概念界定以及各收入成本项目之间的因果关系，构建基于贝叶斯网络的HPPP项目特许期计算模型如图3所示。图中，N1-N6表示引起车流量变动的因素（国家宏观政策、收费标准等），N7-N15表示不同的预期车流量，N16-N17表示引起运营期成本变动的因素（劳动力价格、材料成本等），N18-N20表示不同的预期成本，N21-N47表示运营期车流量和运营成本的不确定性变化产生的不同净利润。

2.3CBN的概率推理

贝叶斯网络中的概率推理过程就是已知证据变量E对查询变量Q进行概率解答的过程，需要进行分析的后验概率为根据贝叶斯法则，有。实际过程中，通常会涉及多个参数，从而增加模型推理的复杂度。通过消元算法可以很好地解决贝叶斯网络概率推理问题，其过程如下：

设贝叶斯网络CBN中所有变量及其概率分布的集合分别为X和£，且£是BN所有联合概率分布 P（X）的一个分解。已知证据 E=e，确定消元顺序ρ：

（1）将£中各证据变量E设置为其直接观测值，从而可得函数显然是e)的一个分解，其中Y=XE。

（2）设Q是Y的一个子集，根据消元顺序ρ，依次从£′中消除所有变量Z，其中Z=YQ，得到函数£″，显然£″是的一个分解。

在HPPP项目CBN模型中，解决问题的基本要求是在已知证据变量的基础上确定具有最大概率的查询变量。根据朴素贝叶斯假设，当类变量给定时，属性变量之间存在条件独立关系，从而有：

式中，α是与c无关的规范化常数。引起项目收入和项目成本不确定变动的风险因素，其发生变化的概率可以结合数据分析和专家咨询得到，然后根据贝叶斯法则即可确定项目收支的条件概率，进而计算分析项目净现值的变化，最后预测既达到项目可行性要求，又满足状态组合概率最大的输出变量。

2.4模拟求解

假设建设期资本投入发生在每期期初，运营期现金流入和现金流出发生在每期期末。根据项目价值评估净现值法的计算方法如下：

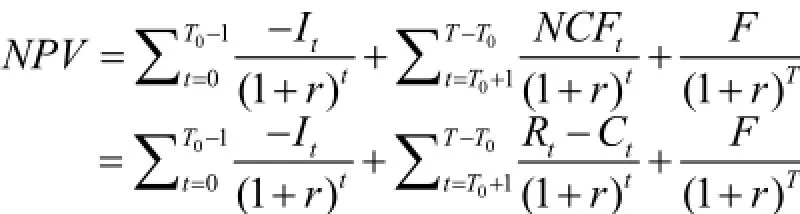
此外，政府部门和社会资本应当同时满足各自项目收益净现值大于等于零，由于本文暂不考虑项目特许经营期结束后移交政府部门运营部分，故社会资本有：

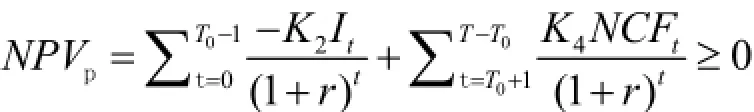
式中，It表示建设期内分期投入的初始成本；政府和社会资本的投资比例分别为 K1和 K2；则有K1+K2=1；T0表示建设期；T表示HPPP项目特许经营期；F表示特许期末项目净残值；r表示现金流量折现率；运营期内收益政府和社会资本的分享比例分别为K3和K4，且K3+K4=1。由于项目的建设期较短，因此在可预测能力之内，项目的建设期可以基本确定。通常，对于公路PPP项目，其运营期可以无限长，净残值F有时可为零。根据HPPP项目特许期贝叶斯模型，当项目在特许经营期内满足净现值大于等于零时则该项目可行，由此可以预测出科学合理的项目特许经营期范围。

3　案例分析

某省道高速公路采用混合PPP模式，总投资90亿人民币，其中政府投资 25亿元，吸引社会资本投资65亿元。项目建设期3年，建设期初始投资按年投入且每年年初投资比例为3:3:4。项目建设结束后交由私人部门运营，运营期间公路每年维护保养、运营管理、巡查收费等需要投入大量的人力、物力和财力，其中人工成本和材料成本所占的比重最大，其不确定性变动受劳动力市场和商品市场供求关系的影响。政府和社会资本通过协商确定的利润分享比例为3:7。项目净残值为总投资额的5%，折现率参考同期银行贷款利率且为固定利率为10%，企业所得税税率为25%，暂不考虑其他税率。

根据经济学家预测，中国经济已经接近但尚未达到增长瓶颈，近几年国家经济增长率大致在4%～6%之间，未来十几年，中国经济潜在增长在6%～7%左右，因此将国家宏观经济发展水平分为3种情况；国家物价局规定的道路收费标准是针对不同类型和规格的车辆进行收费，根据其规定换算，预测该PPP项目平均收费价格约为35.36元/辆，因此也将收费标准（前期预测阶段）分为3个不同的价格区间，如表2所示。

图3　混合PPP项目CBN模型

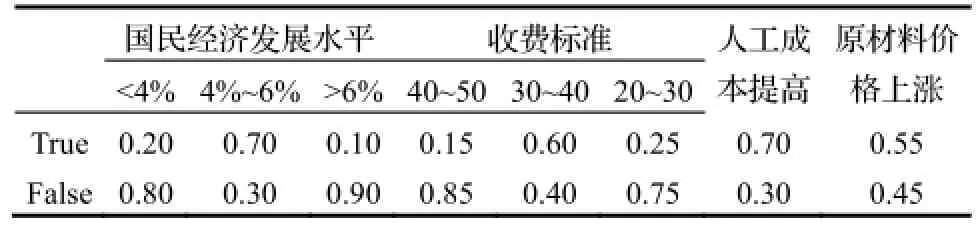
表2　项目收支因素概率分布表

从长期来看，由于国家宏观经济发展和收费标准的制定存在不确定性变动，不同因素之间的结合节点众多，为了更加准确和详细地描述节点之间的依赖关系以及HPPP项目特许期贝叶斯模型的决策有用性，暂将项目生命周期进行间隔划分，以每五年一个阶段进行分析。第一个五年期间的项目特许期CBN模型如图4所示。

由图可知，第一个五年期间运营期的净利润值存在 27种最可能情况。对模型中一种利润情况进行贝叶斯分析，见图5。

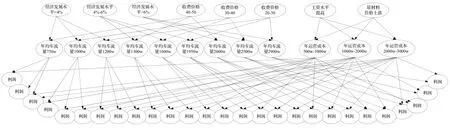
图4　第一个五年期间最可能的特许期贝叶斯网络图

图5　情况一分析

设定各证据变量的概率取值为真，根据图5所示，查询变量取值也为真的情况下，上述情形项目运营期净利润在 23000～35500万元之间的概率为47.76%，即 P（23000w＜profit＜35500w|E=e）= 47.76%。同理在第一个五年期间的其他最可能的26种净利润范围情况也会存在 26个概率值，从而存在一个概率最大的净利润区间范围选项 p(profit)max及其对应的NCFprofit,1。

以此类推，在以后的每一个五年期贝叶斯网络图中都会存在一个概率最大的净利润区间范围和对应的NCFprofit,i，其中i是按时间序列五年期的个数。第二个五年期间及以后，收费价格逐渐确定下来，其最可能的CBN模型，如图6所示。

由此可得，每一个五年期间各项组合的利润范围、项目净现值、私人投资净现值及其概率预测如表3所示，其中第一个五年期间选取概率前8的组合，第二至第四个五年期间选取概率前三的组合，概率相同时净现值大者优先。

建设期及初始投资成本确定的情况下，每过一个五年期都可以进行折现，然后选取概率最高的组合进行净现值分析；当同时满足项目自身和社会资本净现值大于等于零时，即可确定一个合理的特许期范围。由表3可知，项目净现值与私人投资净现值为正的组合出现在第四个五年期间，分别为212569.73万元和130736.81万元，即根据贝叶斯模型估测的PPP项目特许经营期为15～20年，对应的最大概率为 50%；当项目生命周期划分间隔缩小时，将会得到满足条件的、更加准确的特许期范围。

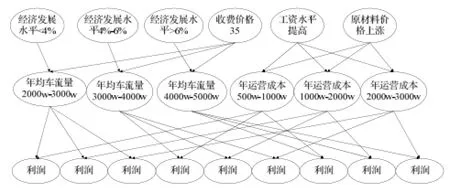
图6　第二个五年期间最可能的特许期贝叶斯网络图

4　结语

在混合PPP项目中，项目特许经营期的科学确定是项目协议的重要一环。本文主要在以往研究PPP项目特许期方法的基础上考虑变量之间的相关关系，并采用贝叶斯网络的方法构建变量之间的因果关系模型，借以确定混合PPP项目特许期的区间范围。结果表明，基于贝叶斯网络的PPP项目特许期计算模型可以对一些基础设施建设项目进行特许期预测并进行有效决策，为科学合理地确定PPP项目特许期增添新的思路。

为了便于计算分析，本文并未考虑项目建设期间的零星收益以及运营期结束移交政府运营部分，除企业所得税之外的营业税、土地增值税等未考虑在内。此外，从长期来看，折现率并非一成不变，通货膨胀等因素对市场经济的影响是不可估量的。未来的研究还需综合考虑更多不确定性因素进行相关分析。

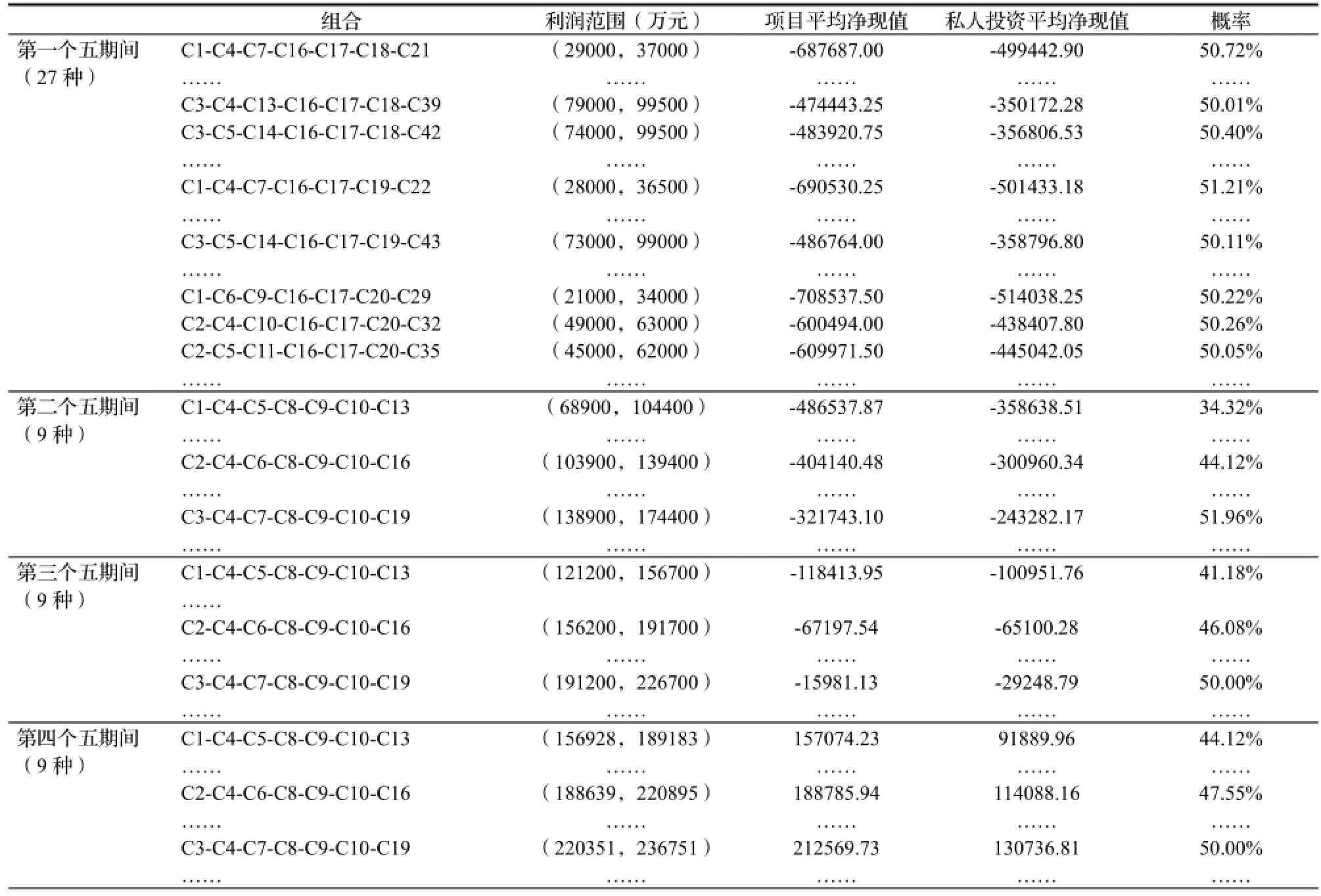
表3　各期间概率组合表

[1] Zhang S，Gao Y，Feng Z，et al．PPP application in infrastructure development in China：Institutional analysis and implications[J]．International Journal of Project Management，2015，33（3）：497-509．

[2] Hanaoka S，Palapus H P．Reasonable concession period for build-operate-transfer road projects in the Philippines [J]．International Journal of Project Management，2012，30（8）：938-949．

[3] 王东波，宋金波，戴大双，等．不确定收益下公路BOT项目特许期决策方法研究[J]．预测，2010（2）：58-63．

[4] 刘 伟，吕俊娜，邹 庆．收益不确定下交通BOT项目特许期决策模型[J]．系统工程，2012，30（12）：51-56．

[5] 张俊生，王广斌．分期 BOT项目期权定价特许权期的决策模型与分析[J]．同济大学学报（自然科学版），2012，40（9）：1434-1438．

[6] Carbonara N，Costantino N，Pellegrino R．Concession period for PPPs：A win–win model for a fair risk sharing [J]．International Journal of Project Management，2014，32（7）：1223-1232．

[7] Ng S T，Xie J，Cheung Y K，et al．A simulation model for optimizing the concession period of public–private partnerships schemes[J]．International Journal of Project Management，2007，25（8）：791-798．

[8] 周 亮，马金平．工程项目进度风险管理的贝叶斯网络建模与分析[J]．工程管理学报，2012，26（1）：69-74．

[9] Khodakarami V，Abdi A．Project cost risk analysis：A Bayesian networks approach for modeling dependencies between cost items[J]．International Journal of Project Management，2014，32（7）：1233-1245．

[10] 张 芳，马金平，靳小青．混合融资的PPP项目特许期计算方法研究[J]．工程管理学报，2015，29（2）：71-75．

The Study of Analyzing Method on Concession Period of Hybird PPP Project Based on Bayesian Network

SONG Zhi-kai，MA Jin-ping，GUO Xiao-yue
（Business School，Qingdao University，Qingdao 266071，China，E-mail：songzhikai74224@163.com）

Reasonably determining the concession period of PPP projects has been the issue of government and society investors，the key to solve this problem is to analyze how various uncertain factors influence the concession period. In order to study the influences on the time span of project concession which uncertainties and their relationships that related to revenues and costs of HPPP projects during the operation stage exert，and taking into account the requirements of the project feasibility，it combines the Bayesian network and net present value and puts forward the analyzing method on concession period of HPPP project based on bayesian network. Besides，it divides the project life into several part and dicounts the group which have the maximum probality so that it can predict the possible interval range of the PPP project concession period. Through the analysis of actual cases，it prove that this method is feasible and provides a reference for the practical work.

hybird financing；PPP project；bayesian network；concession period

F283

A

1674-8859（2016）02-070-05 DOI:10.13991/j.cnki.jem.2016.02.014

宋志凯（1991-），男，硕士研究生，研究方向：项目管理；

马金平（1960-），男，博士，教授，研究方向：管理信息系统，项目管理；

郭笑月（1992-），女，硕士研究生，研究方向：项目管理。

2016-03-10．