空间机械臂柔性连杆的弯曲形状*

安凯 王飞飞

（山东航天电子技术研究所，烟台 264003）

空间机械臂柔性连杆的弯曲形状*

安凯 王飞飞

（山东航天电子技术研究所，烟台 264003）

研究单连杆旋转柔性空间机械臂的弯曲形状，以确定空间柔性机械臂末端的位置.在考虑连杆变形对力矩影响和曲率表示式中不忽略形状函数一阶导数平方的情况下，利用Taylor展式表示连杆的变形，导出了连杆变形的数学模型.通过降阶方法导出形状函数一阶导数的解析式，并给出了由此解析式利用数值积分确定形状函数的方法.给出了利用二分法确定变形后的连杆在其固连坐标系中最大横坐标的方法.针对一组参数进行了仿真，证实了这种方法确定空间柔性机械臂末端的位置的可行性.

单连杆，柔性机械臂，弯曲形状，曲率

引言

空间机械臂作为航天器上一种重要的工具，可以完成释放、回收卫星以及空间站的在轨装配、维修等各种任务，并可以作为航天员出舱工作的辅助工具，甚至替代航天员的部分工作.为了提高操作的机动性和灵活性，空间机械臂一般都具有轻质、大跨度的特点，这注定空间机械臂是一种柔性机械臂，末端位置的确定成为控制的主要难点［1-3］.柔性机械臂是一个高度非线性、强耦合动力学系统，建立精确的、适用柔性机械臂的数学模型相当困难.常用的柔性机械臂连杆模型有Euler-Bernoulli梁和Timoshenko梁两种，使用较多的是Euler-Bernoulli梁模型.但由于Euler-Bernoulli梁模型忽略了剪切形变导致的力矩变化，也忽略了曲率表示式中弯曲位移一阶导数的平方项［4］，只适用与小变形的场合.此外，由于描述柔性机械臂动力学的数学模型是高阶偏微分方程，一般情况下无法得到该方程的严格解析解.因此需要将方程离散化.离散化方法的优劣直接关系到方程的精确程度.目前常采取的离散化方法大致主要是有限元法、有限段法、集中质量法和假设模态法等.应用较多是有限元方法和假设模态法.有限元方法所建立的系统动力学方程维数十分庞大，不便于后续的控制设计［5-6］.假设模态法的核心是将弹性变形表示为时间t和位置x的分离函数之积的无穷级数形式，即假定

其中w（x，t）为弹性变形φi（x）为第i阶振型函数，qi（t）为与之对应的模态坐标［7-8］.按照数学物理方程中分离变量法的理论，微分方程及其边界条件只要满足一定要求，方程的解就可以展开成Fourier级数［10］，因此将变形表示成（t）无可厚非，但在实际应用中无法将无穷级数用于变形的计算，只能取级数的前几项作为变形近似表示，级数的收敛速度越慢，解的误差越大，因此只能用于小变形的情形［11］.

文献［12］对柔性机械臂的弯曲形状进行了初步研究，得到了一组非线性、时变、强耦合的偏微分-积分方程.由于方程太复杂，要得到精确的解析解几乎是不可能的，因此最终还是采用假设模态法和有限元方法，将此连续系统离散化，即把具有无限多个自由度的柔性体连续离散模型离散为只有有限个自由度的系统，并由此求出连续系统近似解.

与其建立复杂的模型然后求近似解，倒不如建立近似模型直接求解.本文在考虑机械臂连杆变形和不忽略连杆曲率中变形一阶导数情况下，将连杆的变形表示为Talor展式，导出连杆变形的数学模型，通过降阶方法导出变形一阶导数的解析表示式，并由此解析表示式通过数值积分和仿真的形式，给出柔性连杆的弯曲形状和末端的位置.

1 柔性连杆机械臂弯曲形状数学模型

如图1所示，OXY表示机械臂的基座坐标系，Oxy表示连杆的固连坐标系.长度为l、弯曲刚度为EI、质量为m的连杆固连在电机的轮毂上，质量为mp的载荷固连在机械臂的末端.

图1 单连杆柔性关节机械臂的力学模型Fig.1 Mechanicalmodel of flexible jointmanipulator with flexible link

当连杆在基座坐标系OXY中以角位移θ（t）移动时，在坐标系Oxy中连杆上两点（x，y（x，t））和（r，v（r，t））的相对加速度可近似表示为

考虑到空间的失重环境，连杆固连坐标系中连杆上横坐标为r、长度为dr的微元所受的力为

按照Euler-Bernoulli悬臂梁理论，该点的力矩M（x）可表示为

其中，lθ是当坐标系Oxy的旋转角加速度为）时连杆横坐标的最大值，即0将 Taylor展式

而

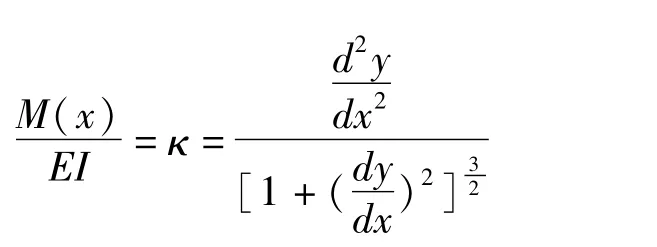
其中κ为点（x，y（x，t））处的曲率，因此

2 数学模型的解

在方程（1）的解求出之前lθ为待定参数，求解过程中取其初值lθ=l.令u=y′（x）则方程（1）化为

两边积分得

令x=0并利用u（0）=y′（0）=0得

因此

由于

即

其中

Cardan方程（1）有唯一实根

因此

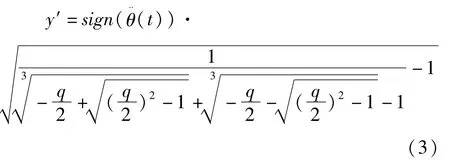
3 待定参数lθ的确定

为强调导数的表示式（3）与lθ的关系，不妨将y′（x）表示为ylθ′（x）.在连杆质量和（t）一定的情况下，连杆越长，连杆同一截面上受到的弯曲力矩越大，连杆也越弯曲，因此，ylθ′（x）是lθ的增函数.当lθ=l时，通过数值积分可以求出弯曲连杆的长度

则

4 仿真

图2 连杆曲线的导函数Fig.2 Derivative of link curve

经计算得

s（l）=2.2166

令横坐标最大值的初始值lθ=2l-s=1.7834，利用二分法经计算lθ，可以求出当lθ=1.8061时

图3 柔性连杆的弯曲形状Fig.3 Bending shape of flexible link

由数值积分可得，连杆末端在连杆的固连坐标系Oxy中的坐标为（1.8061，0.8190）.

图4 弯曲形状随的变化Fig.4 Variation of bending shape with

5 结论

连杆弯曲形状在作为连杆移动坐标系中的函数，既与横坐标x有关，也与连杆旋转角加速度（t）有关，而且x和（t）是相互独立的变量，即y=f （x，（t））.从等式（3）和图4都还可以看出，该函数显然不是（t）的线性函数.由等式（1）可知，不同的（t）所对应的曲线仅有原点一个交点.

当连杆长度l一定时lθ也是（t）的函数，它随（t）的增大而减小.

1 Boizot N，Gauthier J.Motion planning for kinematic systems.IEEE Transactions on Automatic Control，2013，58 （6）：1430～1442

2 Brandt H.Riemannian curvature in the differential geometry of quantum computation.Physica E：Low-dimensional Systems and Nanostructures，2010，42（3）：449～453

3 Javier M V，Luis G H.Operational space trajectory tracking control of robotmanipulators endowed with a primary controller of synthetic joint velocity.ISA Transactions，2011，50（3）：131～140

4 王雪葵.柔性臂的动力学模型与控制的研究［博士学位论文］.沈阳：东北大学，2011（Wang X K.Research ondynamical modeling and control of flexible manipulators ［PhD Thesis］.Shenyang：Northeastern University，2011 （in Chinese））

5 刘燕，张伟，王冬梅.可伸缩复合材料悬臂梁的非线性动力学建模及分析.动力学与控制学报，2014，12（1）：24 ～29（Liu Y，Zhang W，Wang D M.Nonlinear dynamics modeling and numerical analysis of telescoping-and-translating composite laminated cantilever beam.Journal of Dynamics and Control，2014，12（1）：24～29（in Chinese））

6 安凯.由Z传递函数确定PID控制器参数.光电工程，2001，28（6）：7～9（An K，Ma Jiaguang，Fu Chengyu. PID controller parameters determined by Z transfer function.Guangdian Gongcheng，2001，28（6）：7～9（in Chinese））

7 Habib E，Saeed D.Complete dynamic modeling and approximate state space equations of the flexible link manipulator.Journal of Mechanical Science and Technology，2012，26（9）：2845～2856

8 Sachindra M.Shape optimization of revolute-jointed single link flexiblemanipulator for vibration suppression.Mechanism and Machine Theory，2014，75（1）：150～160

9 Steve U，Jurek ZS.Modeling and directadaptive control of a flexible-Jointmanipulator.Journal of Guidance，Control，and Dynamics，2012，35（1）：25～39

10 Lipman B.partial differential equation and solitary waves theory.Beijing：Higher Education Press，2009，69～106

11 杨永泰，荣吉利，李健等.双柔性空间机械臂动力学建模与控制.兵工学报，2014，35（7）：1003～1008 （Yang Y T，Rong J L，Li J，et al.Dynamic modelingand control of space manipulator with flexible joints and links.ACTA Armamentarii，2014，35（7）：1003～1008 （in Chinese））

12 杨辉.刚-柔耦合动力系统的建模理论与实验研究.上海：上海交通大学，2002（Yang H.Study on dynamic modeling theory and experiments for rigid-flexible coupling systems.Shanghai：Shanghai Jiaotong University，2002（in Chinese））

13 安凯，邢进生，邱祖廉.模糊神经网络的二阶段变半径随机搜索算法.自动化学报，2000，26（5）：616～622 （An K，Xing JS，Qiu Z L.Two-stage random search algorithm of fuzzy neural network with variable radius.Zidonghua Xuebao/Acta Automatica Sinica，2000，26（5）：616～622（in Chinese））

BENDING SHAPE OF SPACE MANIPULATOR WITH FLEXIBLE LINK*

An Kai Wang Feifei

（Shandong Aerospace Electro-technology Institute，Yantai 264003，China）

This paper dealswith the bending shape of spacemanipulator with a rotating flexible link in order to determine the position of the ends of the spacemanipulator.Using Taylor expansion，themathematicalmodel of link deformation is obtained considering the effect of link deformation on moment aswell as the square of its first derivative in moment and curvature expressions.Based on themathematicalmodel，an analytical formulation of first derivative on link deformation is obtained by order reductionmethod.The shape function of link is therefore obtained by numerical integration of the analytical formulation.Moreover，amethod to search themaximal abscissa of bending link in fixed coordinate frame using dichotomy is put forward in this paper.It is also validated against simulation results that thismethod is feasible to determine the position of the ends for spacemanipulator.

single-link，flexiblemanipulator，curvature Received 19 March 2014，revised 07 April 2015.

E-mail：ankai2007@163.com

10.6052/1672-6553-2015-019

*National Basic Research Program of China（2013CB733000）

2015-03-19收到第1稿，2015-04-07收到修改稿.

*国家重点基础研究发展计划（973）资助（2013CB733000）

E-mail：ankai2007@163.com