双息信号的斜投影滤波性能

窦慧晶， 陈凤菊， 王千龙, 肖登亮

(北京工业大学电子信息与控制工程学院, 北京　100124)



双息信号的斜投影滤波性能

窦慧晶， 陈凤菊， 王千龙, 肖登亮

(北京工业大学电子信息与控制工程学院, 北京100124)

在干扰信号为完全极化信号的条件下，基于斜投影滤波技术，为了研究双息信号极化敏感阵列的抗干扰性能，利用信号的极化矢量满足列满秩的特性，构建所需的斜投影滤波算子，利用算子与特定运算的性质，抑制掉干扰信号，完整保留期望信号. 利用矩阵共轭转置，矩阵求逆以及特征分解等矩阵运算，推导出了针对双息信号滤波的斜投影算子，并对算法进行仿真. 同时分析到达角、极化参数估计误差等因素对阵列滤波性能的影响. 仿真结果验证了该算法可以有效抑制双息信号中的干扰信号.

双息信号； 极化敏感阵列； 斜投影算子； 特征分解

极化敏感阵列具有获取入射信号完备的电场分量和磁场分量的能力，因而其系统性能比传统标量阵列更加优越[1-3]. 在极化敏感阵列滤波方面，传统极化滤波算法，根据正交投影的原理，利用与干扰极化正交的矢量抑制干扰，忽略了目的信号的极化状态，导致抑制干扰的同时，引入极化损失，而零相移瞬时极化滤波是在传统极化滤波的基础上，对传统算法引入的极化损失进行了幅度/相位补偿，文献[4-6]提出的斜投影技术，利用斜投影算子特定的运算特性，与极化信号矢量相结合，将干扰极化矢量对应斜投影的零空间，实现滤波，不必再进行线性变换和补偿来分离目标和干扰，且无极化损失. 文献[4]中，在干扰极化状态较难估计的条件下，阵列接收信号的协方差矩阵与期望信号的极化矢量可构造斜投影算子，实现极化滤波. 综上所述，对于极化敏感阵列滤波性能的研究仅仅局限于单信号发射模式(single signal transmission，SST)，对双信号发射模式(dual signal transmission，DST)无太多相关研究.

随着阵列系统在移动通信领域的引入，空域信息成为各开发技术的一大资源，例如，智能天线，基于不同的信号方向区分信号，实现信道的空分复用，成倍地增加了系统的容量. 由于信道资源的紧张，各种增加系统容量的多址技术在不断地发展完善，极化多址的思想也得到了发展. 极化多址即根据电磁信号极化状态的不同来区分信号，即使两路电磁信号时域、空域信息相同，当他们的极化状态满足一定条件时，极化敏感阵列就可以根据他们的极化状态将其区分，极化多址技术与其他多址技术一样，大大增加了信道容量，为信道资源拓展了新的领域.

在雷达通信领域，文献[7-9]中,部分极化波可分解为2个传播方向相同但极化状态不同的完全极化波，其两对极化参数互异，则对应的极化矢量线性无关，文献[7]根据部分极化波的这一特性，可同时传送两路信号，这两路信号携带不同的信息，并且同时传输、共用同一频率，共用同一传播方向，唯一的差异就是两路信号的极化状态不同，即DST对应的信号则称为双息信号. 双息信号充分利用了电磁波的2个空间自由度，这在现有和新兴的经济通信技术研究中具有重要意义.

文献[3]提出用基于正交投影原理的传统滤波算法对双息信号进行滤波时，双息信号的两路信号之间无互扰传输的充分必要条件是两期望信号的信号矢量在以干扰噪声协方差矩阵的逆矩阵为加权矩阵的内积空间相正交，而且期望信号通过传统滤波算法滤波后，其极化信息遭到破坏，无法再次利用. 本文针对双息信号传统滤波算法的这2个弊端，利用斜投影技术、多维矩阵构造斜投影算子，对极化敏感阵列接收的双息信号进行滤波，抑制干扰，对两期望信号的正交性并无要求，大大降低了对期望信号矢量的要求，滤波后保留完整期望信号(双息信号)，并分析了参数估计误差对滤波性能的影响，验证其鲁棒性.

1　阵列结构与信号模型

1.1三维极化敏感阵元

文献[6]的三维极化滤波中，阵元由3个中心重合且互相垂直的线极化天线构成，分别接收来自水平方向和垂直方向的极化回波信号，如图1所示．

假设极化敏感阵元位于坐标原点,(θ,φ)为信号波达方向，根据空间电磁信号极化域- 空域联合表征，阵元接收的完全极化信号电场极化矢量为

(1)

式中：Ex、Ey、Ez分别为极化矢量在x、y、z方向上的分量；(γ,η)为信号极化参量.

1.2接收信号模型

由文献[3]知，完全极化波的极化相干矩阵为奇异矩阵，其秩为1，而对于任意的部分极化波，其极化相干矩阵均为满秩的Hermitian矩阵，因此可以进行如下特征分解.

因而，在不考虑互耦效应时，宽带信号的每个频段上的接收数据协方差矩阵为

(2)

该式说明任意一个部分极化波可以分解为2个完全极化波的合成，这2个完全极化波的极化状态正交且不相关.

双信号发射模式[10]：利用部分极化波沿同一方向可同时传送2路独立的信号，即所谓双信号发射模式，对应的信号则为双息信号.

双息信号的极化矢量可写为

(3)

当期望信号为双息信号时，2路独立信号的信号波达方向一致，其极化矢量线性无关，三维极化敏感阵元接收的信号电场极化矢量为

(4)

干扰信号为完全极化信号，阵元接收的干扰极化矢量为

(5)

假设空间有M个干扰信号，则阵元接收信号为

x(t)=s1(t)+s2(t)+i(t)+n(t)=

(6)

式中：as1(t)和as2(t)分别表示期望信号中2路信号的时域信号；am(t)表示干扰信号的时域信号；s1(t)、s2(t)为2路期望信号矢量；i(t)为干扰信号矢量；n(t)为阵列接收机噪声矢量.

因为s1(t)、s2(t)都承载着有用的信息，文献[11-13]在接收端需要将两路信号解调分离，所以运用2套系统来处理，如图2所示，Esi1、Esi2分别为针对期望信号s1(t)、s2(t)的极化滤波矢量.

2　斜投影技术应用于双息信号

2.1斜投影算子

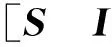
(7)

式中：H为矩阵的Hermitian共轭转置；上标†为矩阵的广义逆.

根据文献[14]，斜投影算子具有如下性质：

EsiS=S,EsiI=0

(8)

即与其相对应的投影空间〈S〉为斜投影算子的值域空间, 子空间〈I〉是斜投影算子的零空间的一个子集. 斜投影算子并不要求2个子空间正交，是正交投影算子的推广.

2.2构建双息信号斜投影极化滤波算子

根据斜投影算子的性质，本文构建斜投影极化滤波算子.

为了分析方便，在不影响滤波性能分析的情况下，本文假定信号方位角φ=π/2，另外假定目标和干扰的极化参数即(γs1,ηs1)、(γs2,ηs2)、(γi,ηi)以及θs、θi已知. 不失一般性，考虑期望信号s1(t)的接收，当期望信号s2(t)加入后，相对期望信号s1(t)而言也为“干扰”信号，当存在单个干扰源时，构建斜投影算子的子空间对应的矩阵分别为

(9)

同理

(10)

此处与单信号传输模式不同的是，单信号传输时的干扰子空间仅仅由一个干扰信号的信号矢量构成，为列向量. 则式(6)改写为

x(t)=s1(t)+s2(t)+i(t)+n(t)=

(11)

(12)

展开为

(13)

(14)

其中

p11=sin2γs2sin2γisin2(θs-θi)

p22=1-cos2γs2cos2γi-cos2θssin2γs2-

cos2θisin2γi-

sin2γs2sin2γicos (θs-θi)cos (θs+θi)

sin2γs2sin2γicos (θs-θi)sin (θs+θi)

sin2γs2sin2γicos (θs-θi)sin (θs+θi)

p33=1-cos2γs2cos2γi-sin2θssin2γs2-

sin2θisin2γi-

sin2γs2sin2γicos (θs-θi)cos (θs+θi)

(15)

其中

ρ=sin2γs1[1-cos2γs2cos2γi-

sin2γs2(cos4θs+sin4θs)-

sin2γi(cos2θscos2θi+sin2θssin2θi)]-

sin2γs2sin2γi[cos2γs1sin2(θs-θi)+sin2γs1cos2(θs-θi)]

将式(14)(15)代入式(13)得斜投影算子

(16)

2.3滤波

假定阵列接收的信号R(t)为目标信号Es(t)和干扰信号Ei(t)的混合信号，R(t)经过相应的斜投影滤波算子Esi1作用后得到结果

(17)

式(17)表明, 接收的混合信号经过斜投影算子的处理后，抑制干扰信号，保留了矢量信号s1(t)，该信号仍保留原有的极化信息，无幅度和相位失真. 这就是斜投影极化滤波的基本原理. 同理，可得到矢量信号s2(t).

3　仿真与分析

本文算法中，由于对于期望信号中2路信号的接收原理相同，以下实验只针对一路信号s1(t)的接收.

本文采用均方误差(mean squared error, MSE)准则来衡量滤波器的滤波性能，MSE定义为

(18)

从图3可以看出，当干扰信号的到达角等于信号到达角时，均方误差很大，根据式(18)得，均方误差很大说明输出信号与期望信号的差别较大，即滤波失效.

当θs≠θi时，本文设定仿真条件：θs=15°，(γs1,ηs1)=(25°,60°)，(γs2,ηs2)=(45°,30°)，(θi,γi,ηi)=(30°,65°,30°). 与单信号发射模式做性能比较：

1) 干扰信号极化参数估计误差对滤波性能的影响

从图4中可以清楚地看出，当干扰信号估计的参数误差越小时，MSE越小，滤波性能越好. 与单信号传输模式相比，干扰信号参数估计误差对滤波性能影响的程度基本相同，这说明当干扰信号参数估计误差在一定范围变化时，本文滤波器依然可以保持与单信号传输斜投影滤波器一样良好的鲁棒性.

2) 期望信号极化参数估计误差对滤波性能的影响

从图5中可以清楚看出，当期望信号估计的参数误差越小时，MSE越小，滤波性能越好. 与单信号传输模式相比，期望信号参数估计误差对滤波性能影响的程度基本相同，这说明当期望信号参数估计误差在一定范围变化时，本文滤波器依然可以保持与单信号传输斜投影滤波器一样良好的鲁棒性.

综合图3～5可以看出，本文提出的双息信号斜投影滤波器对双息信号进行滤波处理时，其滤波性能与单信号传输模式相近，验证了斜投影技术在双信号发射模式的适用性.

为了更直观地了解双息信号斜投影交替滤波器的性能，图6给出了以二进制相位调制(binary phase shift keying, BPSK)信号为期望信号，以幅移键控(amplitude shift keying, ASK)信号为干扰信号，在加性白噪声下的仿真结果，极化参数不变.

图6给出了双息信号斜投影滤波器的效果，该滤波器较好地从接收信号中恢复出目的信号. 而文献[3]提出的针对双息信号的传统滤波算法对两期望信号的信号矢量具有特定的要求，而实际信号并不能满足该要求，无法恢复出目的信号，滤波失效，这也说明了双息信号斜投影极化滤波器进一步扩展了极化滤波的适用范围，放宽了极化滤波器的适用条件，完善和发展了极化滤波理论.

4　结论

1) 针对传统滤波算法对双息信号应用的局限性，利用斜投影技术，构建针对双息信号的滤波算子，对双息信号进行滤波，较好地抑制了干扰信号，准确地保留目的信号的矢量信息，表明该滤波器是极化滤波器的完善，具有较大的理论意义.

2) 与单信号传输模式对比，当干扰与期望信号的极化参数存在一定误差时，其滤波效果依然保持良好，验证其鲁棒性较好.

3) 本文不足之处在于无法抑制同方向到达的干扰信号，因为当干扰信号与期望信号的波达方向一致时，不满足构建斜投影算子的条件，无法构建正确的斜投影算子，以致滤波失效，需后续研究改进.

[1] NEHORAI A, PALDI E. Vector-sensor array processing forelectromagnetic source localization [J]. IEEE Transactions on Signal Processing, 1994, 42(2): 376-398.

[2] WONG K T, YUAN X. Vector cross-product direction-finding with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles or loops[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 160-171.

[3] 庄钊文, 徐振海, 肖顺平, 等. 极化敏感阵列信号处理[M]. 北京: 国防工业出版社, 2005: 16-34.

[4] 张钦宇, 曹斌, 王健, 等. 基于斜投影的极化滤波技术[J]. 中国科学: 信息科学, 2010, 40(1): 91-101.

ZHANG Q Y, CAO B, WANG J, et al. Polarization filtering technique based on oblique projection[J]. Scientia Sinica Informations, 2010, 40(1): 91-101. (in Chinese)

[5] 毛兴鹏, 刘爱军, 邓维波, 等. 斜投影极化滤波器[J]. 电子学报, 2010, 38(9): 2003-2008.

MAO X P, LIU A J, DENG W B, et al. Oblique projection polarization filter [J]. Acta Electronica Sinica, 2010, 38(9): 2003-2008. (in Chinese)

[6] 刘爱军, 宋立众, 王季刚, 等. 斜投影三维极化滤波[J]. 哈尔滨工业大学学报, 2012, 44(3): 75-80.

LIU A J, SONG L Z, WANG J G, et al. Three-dimensional oblique projection polarization filtering[J]. Journal of Harbin Institute of Technology, 2012, 44(3): 75-80. (in Chinese)

[7] 王雪松, 徐振海, 代大海, 等. 干扰环境中部分极化信号的最佳滤波[J]. 电子与信息学报, 2004, 26(4): 593-597.

WANG X S, XU Z H, DAI D H, et al. Optimal filtering of partially polarized signal in the interference background [J]. Journal of Electronics and Information Technology, 2004, 26(4): 593-597. (in Chinese)

[8] 王雪松, 邓泳, 李永祯, 等. 部分极化波瞬态极化投影的统计特性[J]. 应用科学学报, 2005, 23(1): 20-25.

WANG X S, DENG Y, LI Y Z, et al. The statistical characteristics of the instantaneous polarization projection of partially polarized waves [J]. Journal of Applied Sciences, 2005, 23(1): 20-25. (in Chinese)

[9] 宋广, 徐振海. 部分极化干扰条件下极化阵列性能分析[J]. 火控雷达技术, 2008, 37(3): 22-24.

SONG G, XU Z H. Analysis of performance of polarized array under partially polarized interference[J]. Fire Control Radar Technology, 2008, 37(3): 22-24. (in Chinese)

[10] 任博, 施龙飞, 王洪军, 等. 抑制雷达主波束内GSM干扰的极化滤波方法研究[J]. 电子与信息学报, 2014, 36(2): 459-464.

REN B, SHI L F, WANG H J， et al. Investigation on polarization filtering scheme to suppress GSM interference in radar main beam[J]. Journal of Electronics & Information Technology, 2014, 36(2): 459-464. (in Chinese)

[11] OSTROVSKY A S, RODRGUE-ZURITA G, MENESES-FABIAN C, et al. Experimental generating the partially coherent and partially polarized electromagnetic source[J]. Optics Express, 2010, 18(12): 12864-12871.

[12] OSTROVSKY A S, RODRGUE-ZURITA G, MENESES-FABIAN C, et al. Simple technique for generating the partially coherent and partially polarized electromagnetic source[J]. Journal of Physics, 2011, 274(1): 121-133.

[13] JIN H, AHMAD M O, SWAMY M N S. Near-field localization of partially polarized sources with a cross-dipole array[J]. Aerospace and Electronic Systems, IEEE Transactions on, 2013, 49(2): 857-870.

[14] 田静. 极化敏感阵列干扰抑制算法研究[D]. 西安: 西安电子科技大学, 2014.

TIAN J. Research on interference suppression algorithms for polarization sensitive array[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2014. (in Chinese)

(责任编辑杨开英)

Oblique Projection Filtering Performance of Dual Message Signal

DOU Huijing, CHEN Fengju, WANG Qianlong, XIAO Dengliang

(College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124， China)

Filtering anti-jamming performance of polarization sensitive array, based on oblique projection filtering technology, was theoretically studied for dual message signal under completely polarized situation. Through the full rank characteristics of signal polarization vector, the required oblique projection filtering operator was built. Interference signal was suppressed and the complete desired signal was retained by the specific operationproperties. In this paper, the operator of dual message signal filtering was deduced by matrix operation, like matrix conjugate transpose, matrix inversion, the eigenvalue decomposition, and so on. Algorithm simulation was conducted. Many factors such as direction of arrival (DOA) of interference and polarization estimation error would affect the filtering performance. The simulation results show that the algorithm can effectively suppress interference in dual message signal.

dual message signal； polarization sensitive array； oblique projection operator； feature decomposition

2015- 03- 24

国家自然科学基金资助项目(61171137)；北京市教育委员会科研发展计划项目(KM201210005001)

窦慧晶(1969—)， 女， 副教授， 主要从事信号处理、信号参量估计方面的研究， E-mail：dhuijing@bjut.edu.cn

TN 911

A

0254-0037(2016)05-0691-06

10.11936/bjutxb2015030078