基于神经网络的伺服机械手LuGre摩擦补偿控制

王三秀， 赵云波， 陈　光

(1.台州学院物理与电子工程学院， 浙江 台州　318000; 2.浙江工业大学信息工程学院， 杭州　150001)



基于神经网络的伺服机械手LuGre摩擦补偿控制

王三秀1， 赵云波2， 陈光1

(1.台州学院物理与电子工程学院， 浙江 台州318000; 2.浙江工业大学信息工程学院， 杭州150001)

针对伺服机械手系统的LuGre摩擦模型参数辨识难，难以建立其精确的数学模型，利用径向基函数(RBF)神经网络的万能逼近特性逼近LuGre摩擦，并作为计算转矩控制器的补偿项. 通过Lyapunov方法证明了系统的稳定性以及闭环系统跟踪误差的收敛性. 仿真结果证明控制算法能对摩擦进行有效补偿，提高了伺服机械手系统的轨迹跟踪控制性能.

伺服机械手； LuGre摩擦； 径向基函数(RBF)神经网络

摩擦是影响高性能伺服机械手控制精度的一个重要因素，然而不管是旋转关节还是平移关节的伺服机械手，都不可避免地存在摩擦[1]. 为了提高控制系统的性能，必须采取有效的摩擦补偿方法减弱或消除摩擦对伺服机械手系统的影响. 建立准确的摩擦模型是实现摩擦有效补偿的关键. 摩擦模型通常有静态摩擦模型和动态模型2种，静态摩擦模型由于不能真实地反映实际摩擦对系统造成的非线性影响，在一些低速、高精度的伺服运动控制系统中，并不能获得满意的结果[2]. 而动态摩擦模型中的LuGre模型给出了任意稳定状态的摩擦特性，包括摩擦滞后现象、静摩擦时的弹簧特性、依赖于速度改变的变临界摩擦力以及stribeck效应等，可以较好地反映实际的摩擦特性[3].

为了克服摩擦给伺服机械手控制系统带来的危害，专家学者们提出了一些摩擦补偿方法以提高系统的性能[4-6]. PID控制简单实用，但由于非线性摩擦可能导致稳态误差或目标位置附近的极限环，使得PID并不适用高精度机械手控制. 有的将摩擦视为一种外界扰动，采用扰动观测器对摩擦进行补偿，但扰动观测器是基于线性控制理论，只对一定带宽信号有效，对于作用于整个带宽区域的摩擦信号还是存在不足；或者采用实验模型的前馈补偿，但由于速度跟踪误差作用，会产生补偿误差. 因此，寻找其他切实有效的摩擦补偿办法仍是人们所关心的问题.

针对伺服机械手存在的摩擦会降低控制系统的性能，本文提出了一种神经网络摩擦补偿控制方案. 采用，径向基函数(radial basis function，RBF)神经网络逼近LuGre动态摩擦模型，并与计算转矩控制相结合. 神经网络能够以任意精度逼近任意非线性函数，可以用来逼近具有非线性特性的摩擦力，只要选取合适的网络结构和训练方法，就可以无需假设摩擦力模型形式，通过离线或在线学习得到与摩擦力对应的网络输出，从而将其补偿[7]. 尤其RBF神经网络是一种3层前向局部逼近网络，可以大大加快学习速度并避免局部极小问题[8]. 应用Lyapunov稳定性理论证明了控制算法的稳定性，并进行了仿真实验验证. 仿真结果表明了控制方案的有效性.

1　系统描述与建模

为了便于问题的描述，这里只考虑具有一个关节的单臂伺服机械手，如图1所示.

(1)

LuGre摩擦模型假设相对运动的2个刚性体在微观上通过弹性鬃毛相接触. 模型的建立基于鬃毛的平均行为，可以描述大多数在应用中能观察到的动、静态特性，能准确描述机械手系统中的摩擦现象. 因此，文中的摩擦力矩考虑的是LuGre模型. 鬃毛的平均变形用z表示为

(2)

LuGre模型的总摩擦力矩描述为

(3)

(4)

式中：σ0和σ1为动态摩擦参数，其中σ0为鬃毛的刚性系数，σ1为鬃毛阻尼系数；Fc为库伦摩擦数；Fs为静摩擦数；α为黏性摩擦因数；vs为Stribeck切换速度.

LuGre模型用一个一阶微分方程描述了诸多摩擦现象，包括库伦摩擦、黏性摩擦、预滑动、可变静摩擦力、Stribeck效应和摩擦滞后等，包含了试验中能观测到的绝大部分特征.

2　神经网络摩擦补偿控制器设计

对于机械手动力学方程，如果不考虑摩擦，可采用

(5)

如果没有摩擦，则转矩控制器(5)是渐近稳定的. 可得到稳定的闭环误差系统

(6)

但对于实际的伺服机械手控制系统，摩擦是客观存在、不可避免的. 将式(5)代入机械手动力学模型式(1)，可得出

(7)

(8)

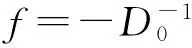
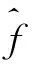
(9)

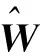
对于任意给定的小正数ε0，必存在一个最优权值向量W*，使得神经网络的逼近误差Δf满足

‖Δf‖=‖W*Tφ(x)-f(x)‖<ε0

取η为神经网络逼近误差，即

(11)

(12)

式中

则式(8)为

(13)

定义Lyapunov函数为

(14)

式中γ>0.

矩阵P为对称正定矩阵，并满足Lyapunov方程

PA+ATP=-Q

(15)

式中Q≥0.

(16)

由于

(17)

因此

(18)

选取神经网络权值调节律为

(19)

式中k1>0.

将神经网络权值自适应调节律代入式(18)，得

(20)

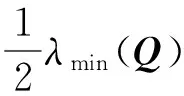
(21)

式中：λmin(Q)为矩阵Q特征值的最小值；λmax(P)为矩阵P特征值的最大值；η0为神经网络逼近误差上界，满足‖ηT‖≤‖η0‖.

式(21)又可以写为

(22)

可见x的收敛半径与λmin(Q)、λmax(P)、η0以及Wmax有关，其中λmin(Q)越大，λmax(P)、η0、Wmax越小，则x的收敛半径越小，系统轨迹跟踪性能越好.

综上，伺服机械手摩擦补偿控制算法完整的控制输入力矩为

(23)

模型并没有考虑外部扰动和参数未建模动态等其他不确定项，如果考虑外部扰动和未建模动态，可以用神经网络同时逼近摩擦项和其他不确定项；模型里仅考虑单关节的情况，对于多关节摩擦问题则可以用多个神经网络分别逼近每个关节摩擦.

3　仿真实验

下面以具体仿真实验，验证本文提出的神经网络摩擦补偿控制算法的有效性.

LuGre摩擦模型参数为：σ0=250，σ1=2.6，α=0.018，Fc=0.26，Fs=0.35，vs=0.01.

为了更好地体现本文提出控制算法的摩擦补偿效果以及轨迹跟踪性能，仿真实验研究将分为2种情况执行，以进行分析比较，分别为单独的计算转矩控制以及本文提出的神经网络控制方法.

第1种情况：采用Simulink实现计算转矩控制算法及带有摩擦模型的伺服机械手的描述. 取Kp=20,Kd=5. 仿真结果如图2所示. 其中图2(a)为关节位置跟踪情况，绿线表示期望运动轨迹，红线表示实际运行轨迹. 图2(b)为关节速度跟踪情况，图2(c)(d)分别为关节位置跟踪误差和速度跟踪误差，可以直观地反映出系统在计算转矩控制器作用下的控制效果. 图2(e)为控制输入信号.

第2种情况：用本文提出的神经网络控制方法对伺服机械手的LuGre摩擦模型进行逼近和补偿，并进行轨迹跟踪控制. 控制器参数选取如下：

神经网络高斯基函数中心和宽度的初始值分别为0.6和3.0. 采用Simulink和S函数进行控制系统的设计，仿真结果如图3所示. 其中图3(a)为关节位置跟踪情况，绿线表示期望运动轨迹，红线表示实际运行轨迹. 图3(b)为关节速度跟踪情况，3(c)(d)分别为位置跟踪误差曲线和速度跟踪误差曲线，可以直观地反映出系统在神经网络控制器作用下的控制效果. 图3(e)为Lugre摩擦及其神经网络逼近，图3(f)为神经网络控制输入信号.

从仿真结果可以看出，单纯地计算转矩控制作用于具有摩擦的伺服机械手，系统跟踪性能并不好，位置跟踪和速度跟踪都存在明显的误差，控制输入信号也不够平稳. 加入神经网络对摩擦进行逼近和补偿之后，系统跟踪性能得到明显改善，实际输出与参考运动轨迹之间跟踪误差趋于零，可见摩擦得到了有效的补偿和抑制. 控制输入信号相较于单独的计算转矩控制也更平稳.

4　结论

1) 针对伺服机械手系统中存在的摩擦会降低系统控制性能，提出了一种神经网络摩擦补偿控制方法. 模型中摩擦力矩选用典型的动态摩擦模型LuGre模型，采用RBF神经网络对LuGre动态摩擦模型进行逼近，并将逼近结果作为计算转矩控制器的补偿项.

2) 通过仿真实验，证明控制算法能对摩擦进行有效补偿，从而提高伺服机械手运动系统轨迹跟踪性能.

[1] MOSTEFAI L, DENAI M, SEHOON O, et al. Optimal control design for robust fuzzy friction compensation in a robot joint[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 3832-3838.

[2] 周金柱, 段宝岩, 黄进. LuGre摩擦模型对伺服系统的影响与补偿[J]. 控制理论与应用, 2008, 25(6): 990-994.

ZHOU J Z, DUAN B Y, HUANG J. Effect and compensation for servo systems using LuGre friction model[J]. Control Theory & Applications, 2008, 25(6): 990-994. (in Chinese)

[3] 刘丽兰, 刘宏昭, 吴子英, 等. 机械系统中摩擦模型的研究进展[J]. 力学进展, 2008, 38(2): 201-213.

LIU L L, LIU H Z, WU Z Y, et al. An overview of friction models in mechanical systems[J]. Advances in Mechanics, 2008, 38(2): 201-213. (in Chinese)

[4] SELMICR R, LEWIS F L. Neural-network approximation of piecewise continuous functions: application to friction compensation[J]. IEEE Transaction on Neural Networks, 2002, 13(3): 745-750.

[5] SALVADOR G V, JAVIER M V. Time-scale separation of a class of robust PD-type tracking controllers for robot manipulators[J]. ISA Transactions, 2013, 52(3): 418-428.

[6] NIELS M, NATHAN V D W, DEVI P, et al. Friction compensation in a controller one-link robot using a reduced-order observer[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 374-382.

[7] DINH H T, KAMALAPURKAR R, BHASIN S, et al. Dynamic neural network-based robust observers for uncertain nonlinear systems[J]. Neural Networks, 2014, 60(1): 44-52.

[8] LIU J K, LU Y. Adaptive RBF neural network control of robot with actuator nonlinearities[J]. J Control Theory Appl, 2010, 8(2): 249-256.

(责任编辑吕小红)

LuGre Friction Compensation Control of Servo Manipulator Based on Neural Network

WANG Sanxiu1, ZHAO Yunbo2, CHEN Guang1

(1.College of Physics and Electronic Engineering, Taizhou University, Taizhou 318000, Zhejiang, China;2.College of Information Engineering, Zhejiang University of Technology, Hangzhou 150001, Zhejiang, China)

To overcome the parameter identification difficulties of the LuGre friction model, and it is not easy to establish an accurate mathematical model, RBF neural network was used to approximate the LuGre friction model, and was combined with the computed torque controller. The stability of the system and the convergence of the tracking error of the closed-loop system were proved by the Lyapunov method. The simulation results show that the control algorithm can compensate the friction effectively and improve the tracking control performance.

servo manipulator; LuGre friction; radial basis function (RBF) neural network

2015- 10- 16

国家自然科学基金资助项目(61304048)；浙江省自然科学基金资助项目(LZ15F030003)； 台州市科技计划资助项目(14GY04)

王三秀(1981—)， 女， 讲师， 主要从事机器人控制、智能控制方面的研究， E-mail: wsx8188@163.com

TG 273

A

0254-0037(2016)05-0679-05

10.11936/bjutxb2015100044