基于AHP—TOPSIS评判模型的长输油气管道风险评价研究

张浩然+徐璐+吴琼

摘要： 针对长输油气管道风险进程随着沿线状况变化而产生波动的实际情况，提出了基于层次分析法（AHP）和逼近理想解排序法（TOPSIS）的长输油气管道风险评判模型。首先对长输油气管道进行准确分段；然后利用AHP确定风险评价指标权重，并通过TOPSIS排序法计算正负理想解和接近度；最后依据接近度对各分段管道风险进行比较分析。实例分析结果表明：基于AHP-TOPSIS的评判模型为长输油气管道的风险管控提供了一种有效的评价依据，具有一定的实用性。

关键词： 油气长输管道；风险评价；层次分析法；逼近理想解排序法

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2016）21-0249-04

Abstract： Aiming at the actual situation that the risk process of long distance oil and gas transportation pipelines fluctuates with the changes along the route， this paper puts forward a long-distance oil and gas transportation pipeline risk evaluation model based on Analytical Hierarchy Process （AHP） and Technique for Order Preference by Similarity to Ideal Solution （TOPSIS）. First， it segments the long distance oil and gas transportation pipelines accurately； Then， it determines the risk evaluation weights with AHP， and calculates the positive and negative ideal solution and proximity with TOPSIS； Finally， it compares the risk of each segment pipeline on the basis of proximity. The analysis results of a real case shows that the evaluation model based on AHP and TOPSIS provides an effective evaluation weight system for the risk management of long-distance oil and gas transportation pipelines. The model is full of some practicability.

Key words： Long-distance oil and gas transportation pipeline；Risk analysis；AHP；TOPSIS

1 概述

在油气运输领域中，由于管道运输的优点突出，促使其成为了油气运输的首选方案，经过长时间发展，长输油气管道也已经成为了工业生产和日常生活中的命脉。油品和天然气一旦泄露，极易导致火灾和爆炸等事故[1]。因此，长输油气管道的事故风险便会给周围地区的人员和财产安全埋下极大隐患[2]。国内外众多学者先后运用不同手段对长输油气管道的风险进行分析，许多系统工程的理论也被应用于预测之中。虽然这些方法取得了一定的效果，但由于大部分事故因素风险分析都是基于长输油气管道整体来进行的，忽略了油气管道跨度大，沿线状况复杂的问题，因而会产生一定局限性。

本文将长输油气管道按照属性合理分段，并引入层次分析法（AHP）和逼近理想解排序法（TOPSIS）[3][4]，提出了用于长输油气管道风险评价的AHP-TOPSIS评判模型。该模型首先利用AHP法将各类因素划分为有序的层次并科学的分配权重，然后结合TOPSIS法构建AHP-TOPSIS综合评判模型。AHP法能够克服TOPSIS法在多因素分析的情况下，确定指标权重难度较大的缺点[5]，同时可以较为客观的给出各影响因素的权值。TOPSIS法能综合考虑多种风险因素，并能够根据有限个评价对象与理想化目标的接近程度进行排序。二者的结合使用能够有效准确的分析长输油气管道各管段的风险大小，为决策提供一种可靠的理论依据。

2指标权重确定

层次分析法（Analytic Hierarchy Process，AHP）是一种将定量分析和定性分析相结合的层次权重决策分析方法。根据目标和需求构建问题的层次结构模型，然后通过专家组对同一层次中各因素进行判断和打分，得出相对重要的权重值，最后根据权重值进行排序，并依据排序结果为选择最优方案提供参考依据[6]。

2.1 层次结构建立

指标体系的建立是整个多属性综合评价的关键，在进行系统分析之后，将复杂问题拆分为具体的元素，并按照不同的属性进行分组，最终形成不同的层次[7]。一般自上而下可分为目标层，准则层和指标层。

假设存在评判对象的指标集：U={U1，U2，…，Un}，其中Ui（i∈[1，n]）是U中的一个指标。Uij={Uij1，Uij2，…Uijn}是Ui中的第j（j∈[1，n]）个指标集，Uijk是该指标集中的第k（k∈[1，n]）个指标集。指标体系的结构模型如图1所示。

2.2 判断矩阵构造

对建立的层次结构，组织评估专家对评价指标体系中的各指标用1～9标度方法进行两两比较打分，从而构建判断矩阵，如表1所示。

设判断矩阵为R，由于每一层指标因素都是以相邻上一层各指标因素作为参照的，因此用上述两元素之比可构造如下判断矩阵：

R为正定互反矩阵，其最大特征根λmax存在且唯一。实际求解判断矩阵R的准确特征值和特征向量W十分困难，因此只能得出近似值。为了得到各因素的权重，可采用方根法求解：将每一列向量归一化，并且求出对应的最大特征根λmax及特征向量W，最后对W归一化。计算公式如式（2）～（4）所示：

2.3 一致性检验及权重向量计算

通常判断矩阵会存在一定误差，为保证权重分配的合理性，需要对判断矩阵进行一致性检验。一致性检验的公式如下：

式中n为矩阵R的阶数，CI为一致性检验指标，CI越小，说明一致性越大。RI为平均随机一致性指标，其与判断矩阵的阶数有关。根据成对比较因子的阶数取不同的值，通常阶数在3和10之间。取值标准如表2所示。CR为判断矩阵的一致性比例，若CR<0.1，认为该判断矩阵通过一致性检验，可以根据该矩阵进行权值计算并求得权重向量，否则不具备一致性，需要重新填写判断矩阵。

3 TOPSIS综合评判模型

逼近理想解排序法（Technique for Order Performance by Similarity to Ideal Solution，TOPSIS法）借助多目标决策问题中正理想解和负理想解之间的距离来对评判对象的优劣进行排序[8]。正理想解是最优的解，其各个属性均达到备选方案中的最佳，而负理想解与之相反，其各个属性均达到备选方案中的最差。然后根据评判对象与理想目标的接近程度进行排序，对现有对象进行相对优劣的评价[9]，如果评价对象更加靠近正理想解，则为最优值，否则为最差值。

3.1 初始评判矩阵

设方案集P={P1，P2，…，Pm}，每个方案评判指标集r={r1，r2，r3，…，rn}，评判指标rij表示第i个方案中第j个评判指标，其中i[1，m]，j [1，n]。初始评判矩阵可以表示为：

3.2 标准化决策矩阵

一般将评判指标分为消耗性指标和收益性指标，对于收益性指标，值越大越好，对于消耗性指标，值越小越好。为了解决各指标量纲和量纲单位不同的问题，消除指标的不可公度性，需要对评判指标进行量纲一化处理[10]。标准化决策矩阵B=（bij）m×n，

收益性指标公式为：

消耗性指标公式为：

3.3 加权标准化决策矩阵

将标准化决策矩阵B的列向量与AHP法确定的总排序权重Wn相乘，得到加权标准化决策矩阵R：

3.4 贴进度分析

J1的正理想解为列向量中的最大值，负理想解为列向量中的最小值， J2的取值与J1相反，如式（7）和式（8）所示。

式中R+为正理想解，R –为负理想解。式（9）表示评判对象与理想解之间的距离。

式中Di+为评判对象与正理想解之间的距离，Di-为评判对象与负理想解之间的距离；rj+与rj-分别为R +与R-相对应的元素。

贴进度分析的公式为：

当评判对象为正理想解时，Ci+=1，当评判对象为负理想解时，Ci+=0，通常评判对象贴进度Ci+取值范围为（0，1），反映评判对象与正理想解之间的贴近程度。

4长输油气管道风险评价实例应用

4.1 长输油气管道风险体系建立

根据美国W.K.Muhlbauer的方案对管道风险因素进行划分，建立的长输油气管道风险体系如图2所示。

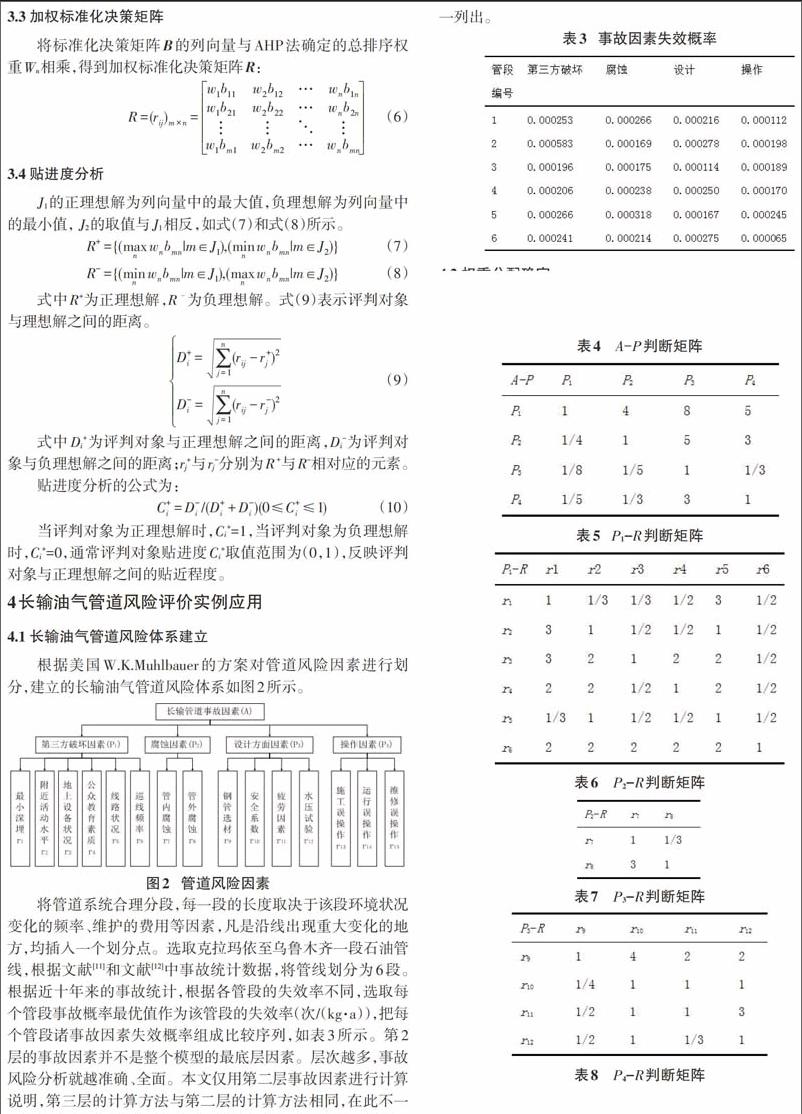
将管道系统合理分段，每一段的长度取决于该段环境状况变化的频率、维护的费用等因素，凡是沿线出现重大变化的地方，均插入一个划分点。选取克拉玛依至乌鲁木齐一段石油管线，根据文献[11]和文献[12]中事故统计数据，将管线划分为6段。根据近十年来的事故统计，根据各管段的失效率不同，选取每个管段事故概率最优值作为该管段的失效率（次/（kg·a）），把每个管段诸事故因素失效概率组成比较序列，如表3所示。第2层的事故因素并不是整个模型的最底层因素。层次越多，事故风险分析就越准确、全面。本文仅用第二层事故因素进行计算说明，第三层的计算方法与第二层的计算方法相同，在此不一一列出。

4.2 权重分配确定

对指标进行重要度评价，构造判断矩阵分别如表4-8所示。

根据表4所示的评判指标重要性程度构造出判断矩阵，由式（1）～（5）得到A-P矩阵最大特征值λmax=4.1487，CR=0.0557<0.1，满足一致性检验，则权重矩阵W=[0.6035，0.2345，0.0506，0.1114]可接受。同理可得：

P1-R矩阵：λmax=6.5203，CR=0.0826<0.1， W=[0.1109，0.1368，0.2276，0.1675，0.0913，0.2659]；

P2-R矩阵：λmax=2.000，CR=0.0000<0.1， W=[0.2500，0.7500]；

P3-R矩阵：λmax=4.2153，CR=0.0806<0.1， W=[0.4442，0.1582，0.2531，0.1445]；

P4-R矩阵：λmax=3.0385，CR=0.0370<0.1， W=[0.6370，0.1047，0.2583]；

层次总排序结果如表9所示。

4.3 TOPSIS法指标综合评判

由表3构建事故因素失效概率的初始判断矩阵为：

因为事故因素失效概率具有同一单位，因此不需要进行量纲一化处理，由式（6）计算得到的加权决策矩阵为：

根据式（7）、（8）可计算得到各管段基于事故因素失效概率的贴进度。其正理想解与负理想解分别为：

根据式（9）计算得到各管段与正理想解和负理想解之间的距离如表10所示。

根据式（10）计算各管段与正理想解的贴进度如表11所示。

由表11可知各管段与正理想解的贴进度排序为：C3+>C4+>C6+>C1+>C5+>C2+。即基于事故因素的各管段失效风险为：管段2>管段5>管段1>管段6>管段4>管段3。

5 结束语

本文提出了一种基于AHP-TOPSIS评判长输油气管道风险评价模型，解决了以往研究只评价事故因素而未考虑长输油气管道风险进程随着沿线状况变化而产生波动的问题。在对长输油气管道分段之后，将AHP-TOPSIS评判模型应用到各管段基于事故因素的失效风险预测上，能够有效预测各管段的风险大小，可作为决策时的理论依据，使管道事故防治更具针对性。

参考文献：

[1] 张胜柱.油气长输管道事故风险分析与选线方法研究[D].北京：中国矿业大学，2012：1-6.

[2] 付建华，王毅辉，李又绿等.油气管道全生命周期安全环境风险管理[J].天然气工业，2013，33（12）：138-143.

[3] 李大全，张鹏，艾慕阳等.模糊聚类法在油气管道风险评价管段划分中的应用[J].天然气工业，2012，32（7）：63-67.

[4] LIN M Y，WANG C C，CHEN M S，et al. Using AHP and TOPSIS Approaches in customer-driven product design process[J]. Computers in Industry，2008，59（1）：17-31.

[5] 陈婷婷，宋永发.基于AHP-TOPSIS的地铁车站施工方案比选[J].工程管理学报，2012 （4）：33-36.

[6] 杜睿山，李阳，曹茂俊，等.基于AHP的油田产能建设项目后评价模型研究[J].计算机技术与发展，2014，24（11）：203-206.

[7] DAI Li， ZHU Ai-hua， ZHAO Yun. Using AHP to calculate optimization objective weights of transplanting mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering，2013，29（2）：60-65.

[8] Zhao H，Xu Z S，Ni M F，Cui F. Hybrid fuzzy multiple attribute decision making[J]. Information，2009，12：1033-1044.

[9] 王新民，秦健春，张钦礼，等.基于AHP-TOPSIS评判模型的姑山驻留矿采矿方法优选[J].中南大学学报：自然科学版，2013，44（3）：1131-1137.

[10] 谢本贤，陈沅江，史秀志.深部岩体工程围岩质量评价的IRMR法研究[J].中南大学学报：自然科学版，2007，38（5）：987-992.

[11] 亓东民. 灰色理论在长输油气管道定量风险评价中的应用[D].兰州：兰州理工大学，2007：24-26.

[12] 王玉梅，郭书平.国外天然气管道事故分析[J].油气储运，2000，19（7）：5-10.