塔里木灌区膜下滴灌棉花水分生产函数及其效益

闫 映 宇

(新疆维吾尔自治区水土保持生态环境监测总站, 新疆 乌鲁木齐 830000)



塔里木灌区膜下滴灌棉花水分生产函数及其效益

闫 映 宇

(新疆维吾尔自治区水土保持生态环境监测总站, 新疆 乌鲁木齐 830000)

以2007—2012年塔里木灌区膜下滴灌田间灌溉试验数据为基础，采用最小二乘法原理，拟合了棉花的水分生产函数模型，分析并计算了棉花最高产量灌溉定额、最佳效益灌溉定额、高效用水灌溉定额，揭示了棉花的水分效应及需水规律。结果表明：塔里木灌区膜下滴灌棉花需水临界期是花铃期和蕾期；产量与耗水量、灌水量均呈良好的二次抛物线关系；合理灌溉定额为3 091～3 464 m3·hm-2，最高产量灌溉定额为3 464 m3·hm-2，高效用水灌溉定额为3 091 m3·hm-2；水资源投入的最佳效益点并非水分利用效率最高点和最高产量点，而是存在于3 091～3 464 m3·hm-2区间；当边际效益等于边际成本时，净收益最大，为24 333.1 元·hm-2，每立方灌水量净收益7.23 元·hm-2；现状条件下最佳效益灌溉定额为3 459 m3·hm-2，产量为6 360.7 kg·hm-2，与最高产量6 360.8 kg·hm-2基本相同，但比最高产量节水5 m3·hm-2，每立方灌水净收益增加0.21 元·hm-2，水分利用效率提高0.003 kg·m-3。

膜下滴灌；棉花；水分生产函数；水分利用效率；灌水效益

棉花是塔里木灌区主要经济作物之一，由于塔里木灌区属于资源型极度缺水地区，而棉花又是高耗水作物，区域水资源不足，直接影响着棉花生产的发展。为解决水资源短缺的矛盾，新疆大力发展节水灌溉技术，提高水资源利用效率。膜下滴灌是新疆绿洲农业最为有效的节水灌溉技术之一，在棉花种植中得到了大面积推广。近年来广大学者针对滴灌条件下土壤水盐运动规律及影响因素、膜下滴灌条件下棉花根系生长、耗水规律等方面进行了深入研究[1-13]，为从根本上探讨水资源的最合理利用方式，确立最优灌溉制度，着力提高水资源利用效率提供了依据。

传统的灌溉目标是向作物提供适宜的水分以获得高的单位面积产量，随着水资源日益紧缺，灌溉费用的增加，要求灌溉不仅要使作物高产，而且要获得最优的经济效益。作物水分生产函数是进行限水灌溉和有限水资源优化调配的基础。国内外有关水分生产函数的研究有很多[14-20]，从不同层次和不同范畴研究了作物的水分利用效率，并建立了各种水分生产函数模型，目的主要是通过模型找到作物需水的关键期，以使有限的水资源发挥更大的作用。一般资源投入与农业产生都存在报酬递减现象，但作物产量和耗水量、水分利用效率之间存在着较为复杂的关系，至今未能得到很好的解决[17]。目前作物水分生产函数可分为两类：一是反映作物产量与全生育期总耗水量关系的水分生产函数称为总水分生产函数；二是反映作物产量与各生育阶段耗水量组合之间关系的水分生产函数称为阶段水分生产函数。我国最常用的模型有相加(Blank)模型和相乘(Jensen)模型，对于作物水分生产函数的研究主要集中在对各种模型的计算方法、建摸和水分胁迫对产量影响的分析上，针对棉花的研究也主要集中在常规灌溉方式上，对膜下滴灌棉花水分生产函数的研究较少。本文试图通过对膜下滴灌棉花水分生产函数的分析，运用边际均衡原理分析灌溉用水量与棉花产量之间的最佳结合点，在获得较高产量的同时，又有较高的灌水效率，能使水资源投入的经济效益达到最佳。为优化膜下滴灌灌溉制度和经济用水提供理论依据和实践指导。

1　材料与方法

1.1研究区概况

试验于2005—2012年在中国科学院阿克苏农田生态系统国家野外科学观测研究站(40°37′N, 80°45′E)进行。该地气候属于暖温带干旱气候，年平均气温11.2℃，与同纬度地区相比，夏季温度偏高、冬季温度偏低、春秋季节气温变化剧烈。多年平均降水量45.7 mm，年水面蒸发量2 500 mm，无霜期207 d，全年日照时数2 940 h，年太阳辐射总量6 000 MJ·m-2。2008年降水量为88 mm，其中棉花生育期4—11月份降水量为80.9 mm。试验地土壤为粉砂壤土。

1.2试验设计

试验采用随机区组设计，灌溉量共设6个水平，分别为：4 265 m3·hm-2(Ⅰ)、3 926 m3·hm-2(Ⅱ)、3 600 m3·hm-2(Ⅲ)、3 271 m3·hm-2(Ⅳ)、2 947 m3·hm-2(Ⅴ)、2 618 m3·hm-2(Ⅵ)，每处理4次重复，小区面积389.2 m2。供试棉花品种为中棉49，株行距采用宽窄行配置(10 cm+65 cm+10 cm+60 cm)，即一膜种植四行棉花，窄行距10 cm，宽行距65 cm，膜间距60 cm，株距均为10 cm。4月28日播种，播种前施磷酸二铵450 kg·hm-2作基肥。全生育期灌溉采用滴灌模式，滴灌带铺设在宽行中央，每7 d滴灌一次，每次灌溉持续7～11 h，6月24日(蕾期)第1次灌水，共灌水10次。在第3～6次灌溉时，随水追施尿素450 kg·hm-2、磷酸二氢钾150 kg·hm-2。

1.3作物水分生产函数理论

1.3.1膜下滴灌棉花滴灌量与产量的关系在灌溉制度一定的情况下，最佳滴灌量与产量的关系，可通过水分生产函数的分析来确定。研究作物水分的消耗和作物产量之间的关系函数，称水分生产函数。为了研究灌溉对作物产量的影响，假定在整个生产过程中，只有水资源一种投入物的数量是不断变化的，且施用技术既定，其他资源如肥料等均被视为固定资源，气候、光照等不可控资源或供应量无法限制的资源也被对照处理所固定。

大量研究表明[17,21-26]，随着水源条件的改善和管理水平的提高，产量与耗水量的关系中出现了一个明显的界限值，当耗水量小于此界限值时，产量随耗水量的增加而增加，开始增加的幅度较大，然后减少；当达到该界限值时，产量不再增加，其后Y随ET增加而减少。因此，作物产量与全生育期总耗水量的函数关系用二次抛物线关系表达，即：

Y=a×ET2+b×ET+c

(1)

式中，Y为棉花的产量(kg·hm-2)，ET为棉花耗水量(mm)，a、b、c为经验系数，通过试验资料确定。

通过膜下滴灌灌水试验资料的统计分析得出：抛物线关系最符合实验区的实际情况。用最小二乘法原理拟合的水分生产函数模型y=ax2+bx+c能够较好地反映膜下滴灌棉花的连续性及生长规律，且参数a、b、c易于估计。因此，采用该模型比较合理，且拟合程度较好，精度较高，易于应用推广。

1.3.2水分利用效率水分利用效率(Water use efficiency, WUE)即水资源的平均生产能力，表示一单位水资源生产的作物产量或生产1 kg作物产量的耗水量，它是节水农业研究的最终目标[17]。作物水分利用效率表达方式有三种，一是用作物耗水量(ET)，这是普遍所指的水分利用效率；二是用灌溉水量(I)，得到的是灌溉水利用效率，它对于确定最佳灌溉定额必不可少，在节水灌溉中意义重大；三是用天然降水(P)，得到的是降水利用效率，它是旱地节水农业中的重要指标。

膜下滴灌棉花水分利用效率可以表示为：

WUE=Y/ET

(2)

式中，WUE为棉花水分利用效率，Y为棉花产量，ET为棉花耗水量。

1.3.3棉花灌水边际效益灌水的边际效益，是指在其他情况不变的条件下，增加一单位水，给生产带来产值的增加量，边际值Mc是边际曲线函数的导数。用公式来表示，则有：

Mc=(ΔY/ΔI)×PY=(dY/dI)×PY

(3)

式中，Mc为边际效益，ΔY为产量的变化量，ΔI为灌水的变化量，PY为棉花单价。随着用水量的增加，水的边际效益是在递减的，边际效益曲线是一条向右下方倾斜的曲线。

灌水的边际成本，是指灌水单价PI，当灌水量增加，边际效益下降但边际成本不变。

灌水的边际利润，是指增加单位灌水成本所增加的灌水利润，用R表示。令灌水利润为B，灌水成本为C，则有:

B=ΔY×PY-C

(4)

dB/dC=d(ΔY×PY-C)/dC=d(ΔY×PY)/dC-1=PY(dΔY/dI)×(dI/dC)-1

(5)

因为：dC/dI=PI

因此式(5)可转化为：

dB/dC=PY×(dY/dI)×(1/PI)-1=(dY/dI)×(PY/PI)-1

(6)

由上式可得出：

dY/dI=(dB/dC+1)×(PI/PY)

(7)

因为：边际利润R=(dB/dC)

则有：

dY/dI=(R+1)×(PI/PY)

(8)

由上式可见：

当R>0时，边际效益(dY/dI)×PY大于边际成本PI，只要继续增加灌水投入量，灌水的净效益仍可继续增加，R值越大，边际效益越高。

当R<0时，边际效益(dY/dI)×PY小于边际成本PI，此时增加灌水投入量所取得的收益已经不能抵偿成本。当R=-1时，dY/dI=0，产量达到最高，此时的灌水量即为最高产量灌水量。

当R=0时，边际效益(dY/dI)×PY等于边际成本PI，收投抵消，净收益最大，此时的灌水量即为最佳效益灌水量。

1.4研究方法

1.4.1土壤水分观测在不同水分处理棉花宽行、窄行、膜间分别埋设中子管，用中子水分仪(CNC503DR)测定0～20、20～40、40～60、60～80、80～100 cm土层的土壤含水量。每隔2 d测定一次，滴灌前后加测。为了解决中子仪测定表层土壤水分不准确的问题，利用烘干法对中子仪进行标定。降雨量取自阿克苏农田生态系统国家野外科学观测研究站。

1.4.2膜下滴灌棉花耗水量确定方法根据农田水量平衡原理，膜下滴灌棉田水量平衡式为：

ET=I+P-(W2-W1)-Q

(9)

式中，ET为棉花耗水量(mm)；I为灌水量(mm)；P为有效降雨量(mm)；W1为时段初80cm土体储水量(mm)；W2为时段末80cm土体储水量(mm)；Q为根系层(80cm)下界面水分交换量(mm)，取向下为正。本研究中通过简化非饱和土壤水运动达西定律获得根区下界面水分通量，非饱和土壤水分运动达西定律如下式：

(10)

式中，θ为根区下界面处的土壤含水率(m3·m-3)，由实测获得；D(θ)为非饱和土壤水分扩散率(mm2·d-1)；K(θ)为非饱和土壤导水率(mm·d-1)，利用已有的研究成果[27]；z为土壤水的高度(mm)。式(10)的中心差分方程为：

(11)

1.4.3数据处理数据采用单因子方差分析(One-way ANOVA)，如果ANOVA结果显著，再用最小显著差数法(LSD)对各处理进行两两配对多重比较。所有统计分析均采用Excel和 SPPS 13.0(SPSS公司，美国)完成。

2　结果与分析

2.1膜下滴灌棉花耗水量与耗水规律

由表1看出，随滴灌量减小，棉花总耗水量减小。由于苗期土壤水分一致，各处理耗水量基本相同，从蕾期开始经过灌水处理，耗水量随滴灌量减小而减小。各处理棉花花铃期耗水量最大，其次是蕾期，苗期和吐絮期较小。各处理棉花的日耗水强度，苗期差异不明显，其值在1.2～1.3 mm·d-1；蕾期以后日耗水强度增大，并随滴灌量的增加而增大。蕾期各处理在2.5～3.3 mm·d-1；进入花铃期后，日耗水强度达到最大值，其值在3.7～5.5 mm·d-1变化；吐絮期又降低，在1.4～2.2 mm·d-1之间。可见，膜下滴灌棉花花铃期是其生育期中耗水强度最大的阶段，耗水量占全生育期耗水总量的50%以上，其次是蕾期，苗期和吐絮期最小。

表1　不同水分处理棉花各生育阶段的耗水量(2008年)

注：不同小写字母表示处理间差异达显著水平(P<0.05)。下同。

Note: Different small letters meant significant difference among different water treatments at 0.05 level. The same below.

2.2膜下滴灌棉花产量与水分利用效率

2.2.1棉花产量、水分利用效率、边际产量与耗水量的关系通过对试验数据进行统计分析、数值曲线拟合，求得塔里木灌区膜下滴灌棉花籽棉产量Y与耗水量ET的关系如下式，相关分析得方程极显著。

Y=-0.1976ET2+212.11ET-50506

(R2=0.9648，n=6)

(12)

式中，Y为籽棉产量,kg·hm-2；ET为耗水量,mm。

对此函数求一阶导数，可得产量最大为6 415 kg·hm-2时的耗水量为537 mm和水分利用效率为11.946 kg·hm-2·mm-1。从图1Y-ET曲线可看出，起初随耗水量的增加棉花产量也逐渐增加，当耗水量达537 mm时，棉花产量最大(6 415 kg·hm-2)，此时灌水边际效益趋于0，水资源在棉花生长发育过程中的短边效应已不存在。如果没有生产条件的重新组合，水资源生产力将表现为负增长，即随灌水量增加，棉花会减产。

棉花水分利用效率是棉花产量与耗水量的比值，由式(12)可得：

WUE=212.11-0.1976ET-(50506/ET)

(13)

从图1中WUE-ET曲线可看出，水分利用效率和耗水量的关系也近似为二次曲线。起初水分利用效率随灌水量增加而增加，当耗水量达到506 mm时，水分利用效率最大，为12.310 kg·hm-2·mm-1；当耗水量超过506 mm后，水分利用效率随着耗水量的增加而减小。显然，从提高水分利用效率的角度考虑，棉花总耗水量以达到506 mm为宜。

图1膜下滴灌棉花产量(Y)、边际产量(M)、水分利用效率(WUE)与耗水量(ET)的关系

Fig.1Relationships between water consumption(ET) and yield (Y) with drip irrigation under mulching, marginal yield(M), and water use efficiency (WUE) of cotton

边际产量M是指每增加1 mm耗水量所能增加的产量，说明了当水分投入增加时所引起的产量变动率，它是Y-ET关系的一阶导数：

M=dY/dET=212.12-0.3952ET

(14)

随着水资源投入量增加，生产力由递增到递减表现了生产函数的一般特性，这个过程体现了水资源生产力的三个不同发展阶段。Y-ET曲线反映的水资源生产力发展的三个阶段，反映了小麦产量与水分关系的一般特征。

第一阶段，从原点至A点之间，生产力迅速增长阶段。边际产量高于水分利用效率，水资源总生产力迅速增长，属于水分极缺区。总产量由最低点上升到水分利用效率最高点，水分利用效率最高为12.310 kg·hm-2·mm-1，此时的耗水量为506 mm，对应产量为6 229 kg·hm-2。在这个阶段，平均每投入一单位水资源所取得的产品量达最大，单位资源投入的成本最小。说明水资源利用尚存在较大的潜力。在这一范围内，在水量条件允许时，应尽可能增加投入，以便获得最大产量。

第二阶段，A点至B点之间，生产力缓慢增长阶段。水分利用效率逐渐降低，属于水分缺乏调节区。随着水资源投入量的增加，资源总生产力继续增长。总耗水量由506 mm增加至537 mm，棉花产量由6 229 kg·hm-2上升到6 415 kg·hm-2，进入水资源投入的高产区，但资源投入的平均生产力或资源利用效率却在下降。从经济意义上看，这一阶段资源得到相对充分利用，资源效益得到较充分发挥。最佳耗水量就在该段范围内，必须严格控制和调节耗水量。

第三阶段，最高产量点B以后，生产力回落阶段。在这一阶段随着水资源用量的增加，总产量不增加反而下降，边际产量为负值，属于奢侈耗水区。在该段越增加水分投入，减产越严重，造成的亏损越大，属于不合理生产阶段。

生产函数三阶段的划分，说明棉花产量与水资源利用效率之间存在着差异，二者并非同步变化。产量的最高点与WUE的最高点不一致，当水资源利用效率达到最高时，棉花产量远未达到最大，相应于WUE最高点的ET要低于Y最高点的ET。例如在Y-ET曲线的顶点B，棉花产量达最大(6 415 kg·hm-2)，其水分利用效率为11.946 kg·hm-2·mm-1。水分利用效率最高时棉花产量6 229 kg·hm-2，与最高产量相差186 kg·hm-2，说明这时水资源潜力尚未充分发挥。在生产中，若单纯追求资源利用效率指标，无异于以资源投入的低效益换取较高的资源利用效率，必然造成水资源的隐形浪费。而若单纯追求产量而忽视资源的利用效率，同样会造成资源浪费和利用不经济。

如果以获得单产最高为灌溉原则，应按B点确定灌溉水量。但在水资源有限的地区，是以有限的水使较小的耕地面积获得最高产量的经济效益大，还是适当减少单位面积的灌水量，以获得最高产量而换取较多的灌溉面积所取得的经济效益大，是灌溉决策者必须认真分析的一个关键问题。

图2膜下滴灌棉花产量(Y)、平均产量(A)、边际产量(M)与灌水量(I)的关系

Fig.2Relationships between irrigation amounts(I) and yield(Y), average yield(A), marginal yield(M) of cotton with drip irrigation under mulching

2.2.2棉花产量、边际产量与滴灌量的关系膜下滴灌棉花籽棉产量(Y)与全生育期滴灌量(I)的关系，经回归分析，符合二次抛物线关系：

Y=-0.0026 I2+18.015 I-24845(R2=0.9592，n=6)

(15)

为了分析灌溉效应，引入灌溉平均产量(A)和灌溉边际产量(M)两个基本概念，且定义灌溉平均产量(A)是指平均每投入单位灌水量所获得的产量[28]，即灌溉水分利用效率；灌溉边际产量(M)是指增加单位灌水量所增加的产量，它是Y-I关系的一阶导数，A、M的单位为kg·hm-2·m-3。

M=dY/dI=18.015-0.0052I

(16)

A=Y/I=18.015-0.0026I-(24845/I)

(17)

由图2可见，三条曲线有两个重要的转折点把Y-I曲线分为三段：第一点是M-I曲线与A-I曲线的交点C，是平均产量曲线的最高点，该点边际产量等于平均产量，灌溉水分利用效率最大，滴灌量为3 091 m3·hm-2；第二点是Y-I曲线的最高点D，该点边际产量M等于零，产量最大，滴灌量为3 464 m3·hm-2，过此点边际产量为负。曲线第一段是从原点到C点，边际产量大于平均产量，产量增加的幅度大于灌水量增加的幅度。此段属于棉花水分极缺区，灌溉量的增加会显著提高产量，因此只要水量允许，就应予以投入；第二段是从C点到D点，虽然边际产量大于零，但已小于平均产量，产量增加的幅度小于灌水量增加的幅度，属于棉花水分缺乏调节区。第三段是D点以后，边际产量小于零，产量随灌水量增大而减小，属于奢侈灌溉区。可见，在第一段内，灌溉的增产效应没有充分发挥出来，在第三段增加灌水量反而导致减产，从节水和经济上看，在第一段和第三段均属于不合理灌溉阶段，第二段属于合理灌溉阶段。

2.3膜下滴灌棉花灌水边际效益分析2.3.1最高产量灌溉定额对于膜下滴灌棉花灌溉生产函数而言，随着滴灌量的增加，棉花产量产值相应增加，当滴灌量增加到一定值时，棉花产量随滴灌量增加的速度变慢，当产量达到最大时，随滴灌量的增加，产量反而下降。边际效益由大到小以至于出现负值。从式(8)可知，当R=-1时，dY/dI=0，此时产量最大(D点)，灌水投入方案为最优方案，最高产量为6 360.8 kg·hm-2，相应的滴灌量为3 464 m3·hm-2，灌溉水分利用效率为1.836 kg·hm-2·m-3。

2.3.2最佳效益灌溉定额在干旱半干旱区，水资源短缺是制约农业发展的关键因素，因此，dY/dI=0虽为灌溉最优方案，但不是最经济方案，当水量投入所增加的产出大于或等于水量投入本身的价值时，即边际收益等于边际成本时的投入方案是最经济方案。设灌溉单方水的价格为PI，籽棉价格PY，从式(8)可知，当R=0时，单位面积上的灌溉利润或收益最大，即：

dY/dI=PI/PY

(18)

由式(16)、式(18)可得到最佳效益灌溉定额为：

I=(PI/PY-18.015)/(-0.0052)

(19)

不同籽棉价格和单方水价格下的最佳效益灌溉定额见表2。

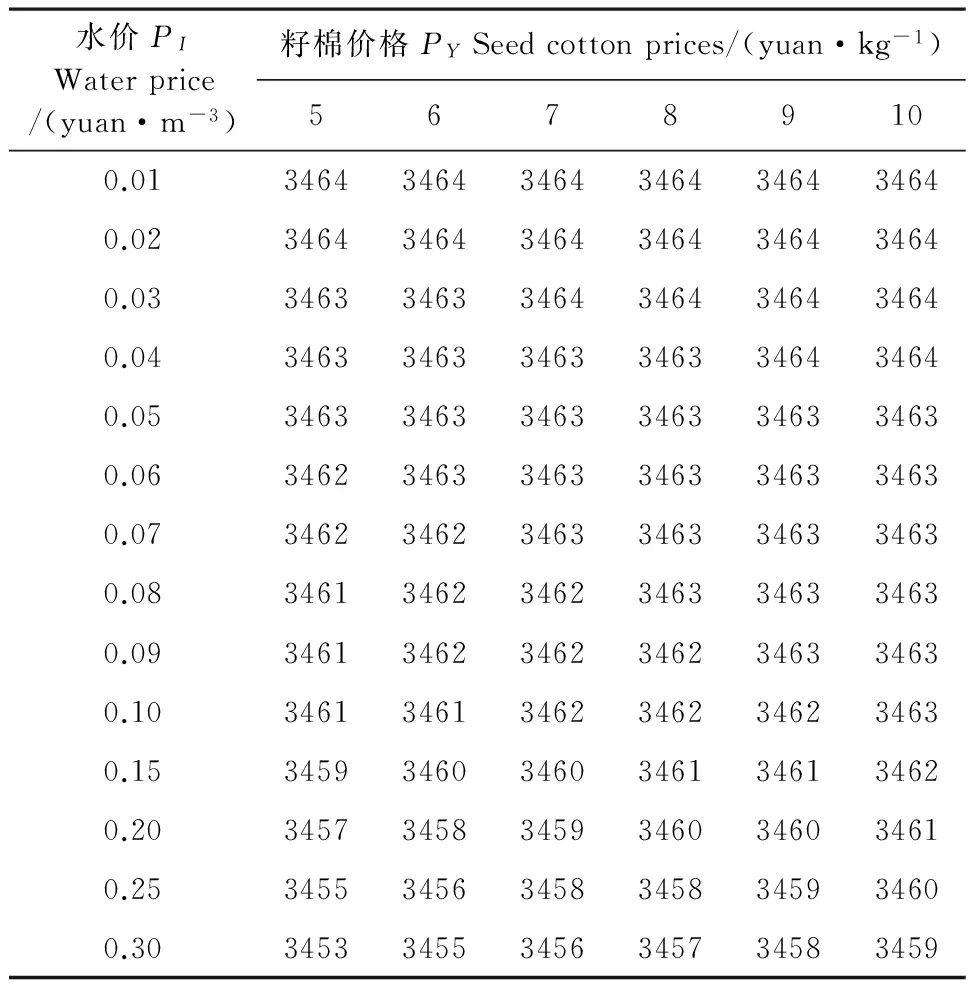
表2　不同籽棉价格和单方水价格下的最佳效益灌溉定额/(m3·hm-2)

由式(19)、表2可以看出，最佳效益灌溉定额不仅与棉花水分生产函数有关，而且与籽棉价格和单方水价格有关，当单方水价一定时，最佳效益灌溉定额随籽棉价格的增加有增加趋势，尤其是在单方水价相对较高时。当籽棉价格一定时，最佳效益灌溉定额随单方水价的增加有减小趋势，但变化趋势不是很明显。由于灌溉用水水价基本恒定，因此不管灌水量为多少，用水的增加和成本的增加都是呈等比例变化的，边际成本不会随着用水量的增加而改变。当水价为0.20 元·m-3，籽棉价格为7 元·kg-1，生产要素不变费用为19 500 元·hm-2时，边际收益等于边际成本时的灌水量，即最佳效益灌溉定额为3 459 m3·hm-2，此时产量为6 360.7 kg·hm-2，较最高产量时的滴灌量3 464 m3·hm-2，节水5 m3·hm-2。此时净收益达到最大，为24 333.1 元·hm-2，每立方灌水量净收益为7.23 元·hm-2。与最高产量点相比，每立方灌水产量由1.836 kg·hm-2增加到1.839 kg·hm-2，水分利用效率提高0.003 kg·m-3，每立方灌水净收益增加0.21 元·hm-2，棉花总产量却基本一致。可见最佳效益点灌水净收益和灌水利用效率较最高产量点均有所增长，但仅比最高产量点节水5 m3·hm-2，且产量基本一致，净收益只增加0.3 元·hm-2，差异不大。这主要是由于膜下滴灌提高了灌溉水利用效率，同时目前单方水价格较低，低水价对最佳效益灌溉定额影响较小。

2.3.3高效用水灌溉定额棉花高效用水追求的目标是单位灌水量所生产出的籽棉产量最大，即灌溉水分利用效率最大。由式(17)可得：

dY/dI=0.0026-(24845/I2)

(20)

当dY/dI=0时，灌溉水分利用效率最大。代入上式得棉花高效用水灌溉定额为3 091 m3·hm-2，相应的最大灌溉水分利用效率为1.941 kg·hm-2·m-3，此时棉花产量为5 998 kg·hm-2。

3　结论与讨论

通过塔里木灌区膜下滴灌棉花灌水实验，得到以下结论:

1) 塔里木灌区膜下滴灌棉花花铃期是其生育期中耗水强度最大的阶段，耗水量占全生育期耗水总量的50%之多，其次是蕾期，苗期和吐絮期最小。棉花的需水临界期是花铃期和蕾期，有限的水资源应首先分配在这两个生育阶段。

2) 塔里木灌区膜下滴灌棉花产量与耗水量呈二次抛物线关系，遵循“报酬递减规律”。水分利用效率最高为12.310 kg·hm-2·mm-1，此时的耗水量为506 mm，产量为6229 kg·hm-2。棉花产量最高为6 415 kg·hm-2时，耗水量为537 mm，水分利用效率为11.946 kg·hm-2·mm-1。根据水分利用效率的变化规律和产量与耗水量的关系，将水资源生产力划分为三个阶段。耗水量小于506 mm为第一阶段，产量随耗水量的增加而增加，属于水分极缺区，在水量条件允许时，应尽可能增加投入，以便获得最大产量。耗水量从506 mm到537 mm为第二阶段，产量仍随耗水量的增加而增加，但增加的幅度减小，生产力缓慢增长，水分利用效率逐渐降低，属于水分缺乏调节区。耗水量超过537 mm以后为第三阶段，产量随耗水量的增加而逐渐减小，出现产量负增长，属于奢侈耗水区，在该段越增加水分投入，减产越严重，造成的亏损越大，属于不合理生产阶段。

3) 塔里木灌区膜下滴灌棉花产量与滴灌量呈二次抛物线关系，产量的最高点与灌溉水利用效率的最高点并不一致，相应于灌溉水利用效率最高点的滴灌量要低于产量最高点的滴灌量。在现有灌溉技术和地下水埋深条件下，膜下滴灌棉花合理灌溉定额为3 091～3 464 m3·hm-2。最高产量为6 360.8 kg·hm-2，其灌溉定额为3 464 m3·hm-2，灌溉水分利用效率为1.836 kg·hm-2·m-3；高效用水灌溉定额为3 091 m3·hm-2，此时棉花产量为5 998 kg·hm-2，灌溉水分利用效率最大，为1.941 kg·hm-2·m-3。

4) 膜下滴灌棉花的最佳效益点并非水分利用效率的最高点和产量最高点，而是存在于3 091～3 464 m3·hm-2区间内，在产量最高点之前。现状条件下边际效益等于边际成本时，净收益达到最大(24 333.1 元·hm-2)，每立方灌水量净收益7.23 元·hm-2，最佳效益灌溉定额为3 459 m3·hm-2，其产量为6 360.7 kg·hm-2，较最高产量滴灌量节约用水5 m3·hm-2，每立方灌水净收益增加0.21 元·hm-2，水分利用效率提高0.003 kg·m-3，而产量基本相同。最佳效益点虽然比最高产量点节约用水5 m3·hm-2，灌水净收益和灌水利用效率均有增长，且产量基本一致，但两点之间的变化非常微小，主要是由于膜下滴灌提高了灌溉水利用效率，同时目前单方水价格较低，低水价对最佳效益灌溉定额影响较小，这也符合报酬递减规律。

[1]吕殿青,邵明安,王全九,等.膜下滴灌土壤盐分特性及影响因素的初步研究[J].灌溉排水学报,2001,20(1):28-31.

[2]吕殿青,王文焰,王全九.滴灌条件下土壤水盐运移特性的研究[J].灌溉排水,2000,19(1):16-21.

[3]李毅,王文焰,王全九,等.温度势梯度下土壤水平一维水盐运动特征的实验研究[J].农业工程学报,2002,18(6):4-8.

[4]王新平,李新荣,康尔泗.干旱沙区滴灌条件下水盐运移过程试验研究[J].干旱地区农业研究,2002,20(3):44-48.

[5]王全九,王文焰,汪志荣,等.盐碱地膜下滴灌技术参数的确定[J].农业工程学报,2001,17(2):47-50.

[6]吕殿青,王全九,王文焰,等.膜下滴灌水盐运移影响因素研究[J].土壤学报,2002,39(6):794-801.

[7]张琼,李光永,柴付军.棉花膜下滴灌条件下灌水频率对土壤水盐分布和棉花生长的影响[J].水利学报,2004,35(9):123-126.

[8]赵成义,闫映宇,李菊艳,等.塔里木灌区膜下滴灌的棉田土壤水盐分布特征[J].干旱区地理,2009,32(6):892-898.

[9]Raine S R, Meyer W S, Rassam D W, et al. Soil-water and solute movement under precision irrigation: Knowledge gaps for managing sustainable root zones[J]. Irrigation Science, 2007,26(1):91-100.

[10]Coelho F E, Or D. Root distribution and water uptake patterns of corn under surface and subsurface drip irrigation[J]. Plant and soil, 1999,206(2):123-136.

[11]闫映宇,赵成义,盛钰,等.膜下滴灌对棉花根系、地上部分生物量及产量的影响[J].应用生态学报,2009,20(4):970-976.

[12]王兴繁,胡顺军,田长彦,等.塔里木灌区棉田蒸散与棵间蒸发变化规律[J].干旱地区农业研究，2012，30(6)：74-78.

[13]刘新永,田长彦,马英杰,等.南疆膜下滴灌棉花耗水规律以及灌溉制度研究[J].干旱地区农业研究,2006,24(1):108-112.

[14]雷成霞,何新林,王振华,等.新疆地下滴灌无膜移栽棉花水分生产函数试验分析[J].灌溉排水学报,2011,30(4):132-134.

[15]金建华,孙书洪,王仰仁,等.棉花水分生产函数及灌溉制度研究[J].节水灌溉,2011,(2):46-48.[16]胡顺军,王仰仁,康绍忠,等.棉花水分生产函数Jensen模型敏感指数累积函数研究[J].沈阳农业大学学报,2004,35(5-6):423-425.

[17]刘昌明,周长青,张士锋,等.小麦水分生产函数及其效益的研究[J].地理研究,2005,24(1):1-10.

[18]王会肖,刘昌明.作物水分利用效率内涵及研究进展[J].水科学进展,2000,11(1) :99-104.

[19]Kipkorir EC, Raes D, Massawe B. Seasonal water production functions and yield response factors for maize and onion in Perkerra, Kenya[J]. Agricultural Water Management, 2002,56(3):229-240.

[20]Rajputgs, Singhj. Water production function for wheat under different environmental conditions[J]. Agricultural Water Management, 1986,11:318-332.

[21]马忠明.有限灌溉条件下作物-水分关系的研究[J].干旱地区农业研究,1998,16(2):75-79.

[22]雷志栋,胡和平,杨诗秀,等.叶尔羌河灌区冬小麦灌溉试验与分析[J].灌溉排水,1999,18(2):30-33.

[23]王修贵,张祖莲,赵长友,等.作物产量对水分亏缺敏感性指标的初步研究[J].灌溉排水,1998,17(2):25-30.

[24]陈亚新.作物-水模型及其敏感指标的确认[J].灌溉排水,1995,14(4):1-6.

[25]Kirda C. Deficit irrigation scheduling based on plant growth stages showing water stress tolerance[C]//Deficit Irrigation Practices. Water Reports 22, Rome:FAO, 2002.

[26]Wang Huixiao, Zhang Lu, DawesW R, et al. Improving water use efficiency of irrigated crops in the North China Plain measurements and modeling[J]. Agricultural Water Management, 2001,48:151-167.

[27]闫映宇,林新慧.灌溉方式对土壤水分运动参数的影响[J].水土保持研究,2011,18(4):160-165.

[28]胡顺军,周宏飞,宋郁东,等.渭干河灌区棉花高产节水优化灌溉制度试验研究[J].灌溉排水,2000,19(4):25-29.

Water production function and efficiency of cotton under mulched drip irrigation

YAN Ying-yu

(GeneralStationofWaterandSoilConversationandEco-environmentalMonitoringofXinjiang,Urumqi,Xinjiang830000,China)

This paper discusses the relationship between the amount of irrigation and the yield of cotton. Statistical analysis of experimental data on cotton under mulched drip irrigation during 2007—2012 indicates that the relationship between yield of cotton and irrigation presents a quadratic parabola in Tarim irrigated area. The irrigation norms for the highest yield, for the highest water use efficiency, and for the highest benefits, and the critical period of water requirement in cotton were analyzed by mathematical method. Best fit model of cotton water production function was adopted by least squares theory on the basis of field experimental data of cotton. Water production function is a quadratic function and its math expression isY=0.0026I2+18.015I-24845 (R2=0.9592，n=6). Water productivity is divided into three different development stages according to the changing rule of water use efficiency and the relationship between yield and irrigation. Irrigation amounts less than 3 091 m3·hm-2are identified as the first stage when yield rises with the increase of irrigation amounts, and productivity rises gradually at this stage. Irrigation amounts at the second stage rises from 3 091 m3·hm-2to 3 464 m3·hm-2and the yield still rises with the increase of irrigation amounts, but the range is reduced. Irrigation amounts at the third stage exceed 3 464 m3·hm-2and the yield is reduced with the increase of irrigation amounts. Negative rise occurs and productivity is declined. The analysis of cotton irrigation production function and the water requirement law indicates that the critical periods of water application for cotton are at the flowering stage and budding stage. The rational irrigation norm, norm for the highest yield, and norm for the highest water use efficiency for cotton are 3 091 to 3 464 m3·hm-2, 3 464 m3·hm-2, and 3 091 m3·hm-2, respectively. The best benefits point of irrigation efficiency of cotton is not the highest point of utilization ratio of water or the highest point of yield, but within the 3 091～3 464 m3·hm-2interval. When marginal benefit equals marginal cost, net income of irrigation on cotton is the biggest. The maximal net income and net income of unit of irrigation amounts are 24 333.1 yuan·hm-2and 7.23 yuan·hm-2, respectively, and irrigation amounts is 3 459 m3·hm-2at this time. Compared with the irrigation norm for the highest yield, it saves 5 m3·hm-2of water, meanwhile water use efficiency and net income of unit of irrigation amounts are increased by 0.003 kg·m-3, 0.21 yuan·hm-2, respectively, whereas the yield is almost the same.

drip irrigation under mulching; cotton; water production function; water use efficiency; irrigation efficiency

1000-7601(2016)04-0018-07

10.7606/j.issn.1000-7601.2016.04.04

2015-11-23

973课题“绿洲化的水、土、气过程及其相互作用机制”(2009CB421302)；中国科学院创新项目(KZCX2-YW-127)

S562；S274.1

A