不同湿润比下滴灌土壤入渗特性模拟试验研究
2016-10-18胡笑涛王文娥
王 平,胡笑涛,王文娥
(西北农林科技大学 旱区农业水土工程教育部重点实验室, 陕西 杨凌 712100)
不同湿润比下滴灌土壤入渗特性模拟试验研究
王平,胡笑涛,王文娥
(西北农林科技大学 旱区农业水土工程教育部重点实验室, 陕西 杨凌 712100)
为了研究滴头流量和设计湿润比对土壤水分运移规律及湿润体特性的影响,前期利用粘壤土进行试验研究,然后依据非饱和土壤水动力学理论和滴灌条件下土壤水分运移特征,建立了土壤水分运动模型,利用HYDRUS-3D对不同湿润比下滴灌土壤入渗模型进行求解。通过所建模型,对11个观测点的模拟结果与实测结果进行了对比,得出灌水结束时各观测点模拟与实测含水率的相对误差均小于10%,实测与模拟湿润比的相对误差为4.75%~11.78%。利用所建模型对不同情景下湿润体运移规律进行了模拟,获得了湿润体特征变化规律:滴头流量主要影响水平湿润锋的运移距离,而设计湿润比对垂直湿润锋运移距离的影响较大;滴头流量相同时,设计湿润比越大,湿润体内平均含水率越大,高含水区(含水率>0.410 cm3·cm-3)半径也越大; 设计湿润比相同时,湿润体内含水率高于0.410 cm3·cm-3的湿润半径随流量增大而增大。
滴灌;湿润比;入渗特性;土壤含水率;数值模拟
滴灌是目前最先进的局部灌溉方法之一,节水增产效果良好。与漫灌、喷灌等不同,滴灌属于点源入渗,地表湿润范围及蒸发量小,灌溉水入渗主要集中在作物根系,有效提高了水分利用效率,由于土壤入渗速率与滴头流量同时影响到土壤水分运动及分布,进一步影响作物根系对水分吸收,因此国内外许多学者都对滴灌条件下土壤水分运移规律及湿润体特性进行了试验研究[1-2]和数值模拟分析。Cote和Siyal都运用Hydrus-3D软件对滴灌条件下的土壤水分及溶质运移进行了模拟和分析[3-4];张林和魏群也利用Hydrus -3D模型对单点源和多点源滴灌条件下土壤水分运移进行了模拟试验研究[5-6]。但是以上研究主要侧重于滴头流量、土壤特性、初始含水率对湿润体的影响,很少涉及关于湿润比对湿润体特性的影响。湿润比[7]是滴灌系统设计的一个重要参数,是把滴灌系统和作物生长的水分状况联系起来的重要纽带。自Keller[8]提出湿润比的概念后,湿润比(Wetted percentage, WP)在滴灌系统的设计中得到了广泛应用,雷廷武[9-10]根据湿润比的定义,从理论上导出了湿润比计算公式的理论基础以及实际应用时应满足的条件;晏清洪[11]通过采用3种滴灌湿润比,探讨了滴灌湿润比对根系分布的影响。本文以不同湿润比、滴头流量的点源滴灌入渗试验为基础,利用HYDRUS-3D软件对水分运移规律进行模拟,研究滴灌土壤水分的运移特征及含水率分布规律,为滴灌系统设计提供理论依据。
1 数值分析模型
1.1土壤水分运动方程
地表点源滴灌土壤水分运动属于典型的三维问题,HYDRUS模型的水流状态为饱和-非饱和达西水流,根据达西定律、质量守恒定律[12],假定土壤均质、各向同性,忽略水分运动时空气、温度和滞后效应对土壤水分运动的影响,土壤水分运动用Richard方程来描述:

(1)
式中,φm为总水势(MPa);K(θ)为非饱和土壤导水率(cm·min-1);θ为土壤体积含水率(cm3·cm-3);t为水分运动时间(min)。
1.2定解条件
1.2.1初始条件求解土壤水分运动方程的初始条件[13]为:
h(x,y,z,t)=h0(x,y,z)0≤x≤X;
0≤y≤Y; 0≤z≤Z, t=0
(2)
式中,h(x,y,z,t)为计算区域的初始负压水头,cm;x、y、z分别为模拟计算区域水平长度、宽度和深度,根据土壤入渗试验分别取x∈[0,30]、y∈[0,30]、z∈[0,70],单位为cm。


图1数值模似计算区域
Fig.1Numerical simulation calculation region
上边界是一个动态边界,参考张林等[14]将上边界分为两种情况考虑:
(1) 滴头流量较小,出流速率小于土壤的入渗速率,水分能够瞬间渗入土壤中,即地表无积水。
在滴头处有:
(3)

(2) 滴头流量较大,出流速率大于土壤的入渗速率,水分不能迅速渗入土壤中,即地表有积水。
在地表饱和区有:
h=0 (0≤x≤Rs,X-Rs≤x≤X,z=0)
(4)
(5)
式中,Rs为地表积水半径,cm。
模拟过程参考李久生[14]文献中的方法:先假定地表积水的半径,用数值模拟的方法来模拟水分运动(模拟灌水量与实际灌水量的误差为5%左右),将滴头流量与时间的乘积近似为土体水量的增加,再通过数值模拟拟合地表积水半径与滴头流量的关系。
由于土箱深度较大,故下边界可认为土壤水分和土壤压力水头保持不变,即:
h(x,y,z,t)=h0,0≤x≤X;t>0
(6)
1.3数值求解
采用商业软件HYDRUS-3D对上述模型进行数值模拟,利用Galerkin有限单元法进行数学模型的数值计算[15],利用隐式差分法对时间进行离散[16]。模型的模拟区域长、宽、高分别为60、60、70 cm的长方体,采用三棱柱进行单元网格划分,网格大小为1.9 cm;滴头附近由于土壤水势梯度较大,对网格进行加密处理;为便于模拟结果的验证,模拟时在沿滴头位置处的1/4竖直剖面上设置了11个观测点,相邻观测点的水平间距和垂直间距均为7.5 cm,观测点具体布置如图2所示。

图2模拟区域观测点布置
Fig.2 Layout diagram of observation points in simulation region
2 模型验证
2.1供试土壤
供试土壤为陕西杨凌西北农林科技大学灌溉排水试验站粘壤土,取土层次为0~40 cm。土壤容重为1.35 g·cm-3,土壤的机械组成为砂粒(0.02 mm)占62.00%,粉粒(0.002~0.02 mm)占32.36%,粘粒(<0.002 mm)占5.64%,土样风干后过2 mm筛备用。
土壤水分特征曲线利用高速离心机测定,土壤饱和导水率用定水头法进行测定,土壤水分特征曲线采用Van Genuchten模型拟合。
(7)
(8)
其中:
Se=(θ-θr)/(θs-θr)
(9)
m=1-1/n, n>1
(10)
式中,θs为土壤饱和导水率(cm3·cm-3);θr为土壤残余含水率(cm3·cm-3);α,n,m为拟合参数;α是与土壤物理性质有关的参数(cm-1)。h为土壤负压水头(cm);Ks为渗透系数(cm·min-1);Se为土壤有效含水率(cm3·cm-3);l为空隙连通性参数,一般情况取为0.5。本研究中土壤水分特性的参数值为θr=0.03cm3·cm-3;θs=0.48cm3·cm-3;α=0.036cm-1;n=1.56;Ks=0.125cm·min-1。
2.2试验装置与方法
通过室内单点源滴灌入渗试验,对所建数学模型进行验证。试验装置由供水系统、有机玻璃土箱和土壤水分测定仪ECH2O组成。供水系统由恒定水头为10 m的水塔和滴头组成,滴头为两种以色列NETAFIM管上式压力补偿滴头,利用水塔向滴头供水,滴头实测流量分别为2.2 L·h-1和4.1 L·h-1;有机玻璃土箱尺寸为60 cm×60 cm×70 cm(长×宽×高);试验过程中采用ECH2O土壤水分测定仪实时监测土壤湿润体内含水率的动态变化,ECH2O由传感器和数据采集器两部分组成。
试验土壤按照容重1.35 g·cm-3分层装土,底层装土厚度为10 cm,上面每层为7.5 cm,装土过程中埋设传感器,共40个,传感器布置图如图3所示,传感器的横向与垂向距离均为7.5 cm;装土结束后自然沉降一天以获得均匀稳定的土壤初始含水率。
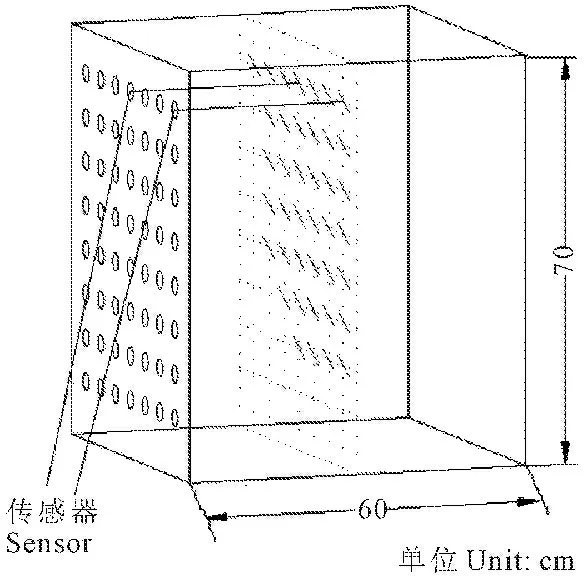
图3传感器布置
Fig.3Arrangement diagram of sensor
试验在相同土壤初始含水率(7%)和相同土壤容重(1.35 g·cm-3)的条件下,分别选择滴头流量为2.2、4.1 L·h-1,设计湿润比为40%、60%、80%水平下开展试验。试验于2014年4—6月在陕西杨凌西北农林科技大学旱区农业水土工程教育部重点实验室进行,试验开始后通过数据采集器监测48 h内湿润体的含水率变化情况,观测时间间隔为2 min。
2.3结果验证
2.3.1土壤含水率表1列出了灌水结束时60%湿润比、滴头流量2.2 L·h-1时,11个观测点实测与模拟土壤含水率的对比结果。由表1可以看出,土壤含水率的实测值与模拟值之间相对误差的绝对值在1.6%~10%之间,此外还可以看出距离滴头越远,含水率的相对误差越大,这可能是由于模拟是在土壤均质、各向同性的理想情况下进行,而实际试验时沉降过程中下层土壤会比上层土壤压实程度大,进而减小了土壤下层水分运移速率,导致实测与模拟含水率之间差值变大。但从总体来看,数值模拟的结果与试验结果基本一致,说明利用所建立的数学模型可以对滴灌的土壤水分运移进行模拟。
2.3.2土壤含水率随时间的变化规律图4为灌水结束时,不同处理下的3个观测点处含水率随时间变化规律的模拟与实测对比情况。从图中可以看出,灌水开始后,观测点距离滴头越近,该观测点的含水率增长速度越快,随着时间推移,含水率增长速度逐渐趋于平缓,总的来看,各观测点处的含水率都呈先增大后趋于平缓的趋势。通过模拟值与实测值对比,可知模拟和实测的含水率变化规律基本一致,各观测点的模拟值与实测值均较接近,相对误差(相对误差=|模拟值-实测值|/实测值)均小于10%,模拟结果能较好地反映湿润体内含水率的变化情况。
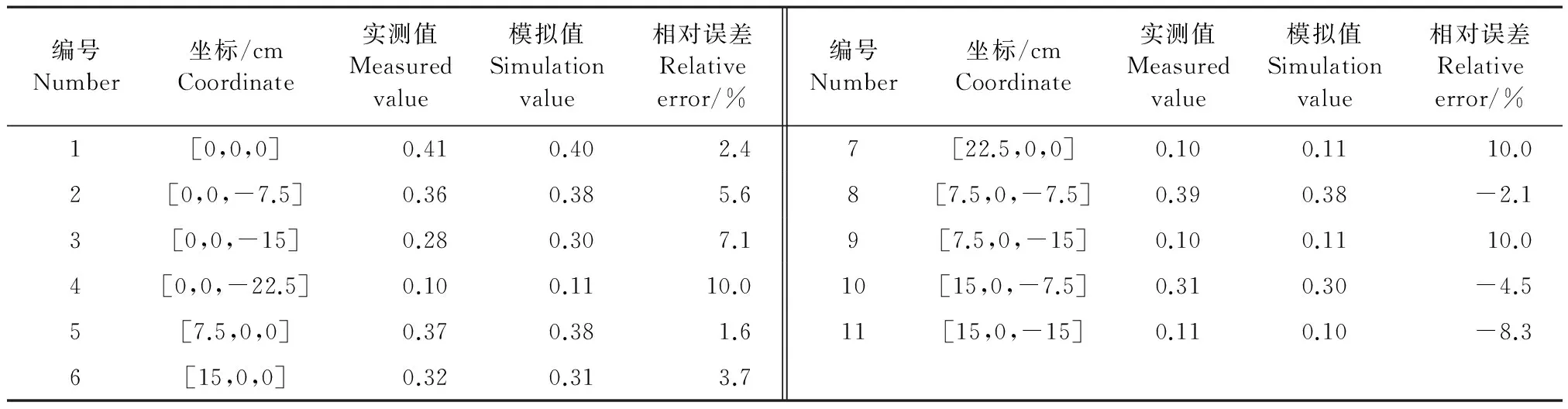
表1 土壤含水率实测值与模拟值的对比

图4土壤含水率试验值与模拟值对比
Fig.4Comparison of measured and simulated soil moisture
2.3.3湿润比的变化规律表2给出了灌水结束时,不同处理下实际与模拟湿润比的对比情况,由表中可以看出,模拟湿润比均稍大于实际湿润比,实际与模拟湿润比的相对误差变幅在4.75%~11.78%之间,误差原因可能是由于装土阶段土壤夯实不均匀或由于仪器测量误差造成的。总体来看,模拟结果仍可以很好地代表实测结果,表明所建模型可用于实际湿润比的计算。
3 结果与分析
利用所建模型对湿润比分别为40%、50%、60%、70%、80%,滴头流量分别为2.2、3.0、4.1、5.0 L·h-1情况下湿润体的运移特征进行了模拟,并分析了模拟结果的湿润体特性变化规律。
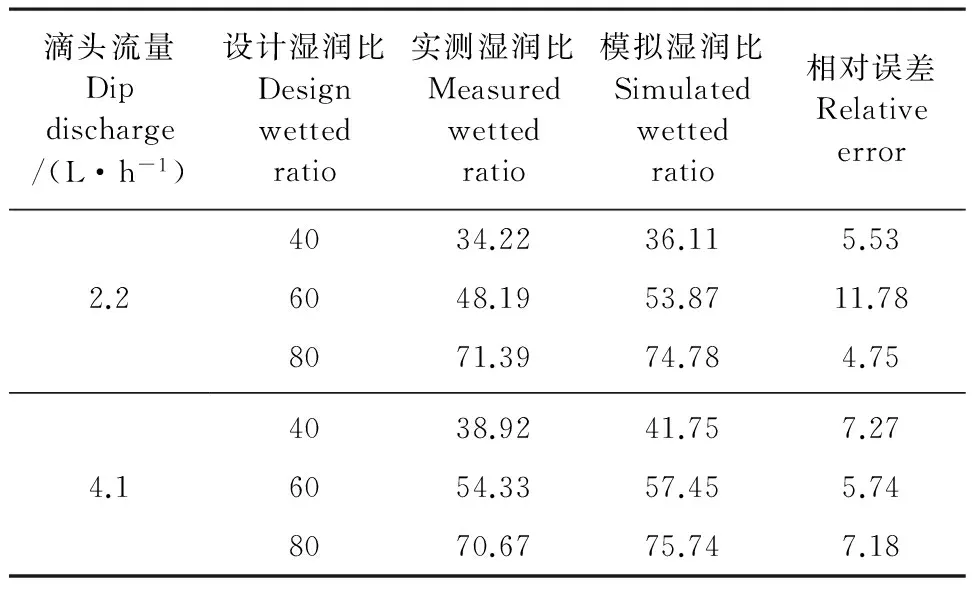
表2 湿润比实测值与模拟值的对比/%
3.1流量和设计湿润比对湿润体形状的影响
表3为模拟的不同设计湿润比和滴头流量下湿润体的深宽比(H/x,湿润体在垂直方向运移距离与水平方向运移距离的比值)变化规律。由表3可以看出,相同设计湿润比时,深宽比随滴头流量增大而减小,说明滴头流量对水平运移距离的影响较大,滴头流量较小时(2.2、3 L·h-1),湿润锋的垂直运移距离大于水平运移距离,这是因为滴头流量越大,土壤入渗能力越小于供水强度,土壤表层积水半径越大,加速了积水区在水平方向的运移速率;滴头流量相同时,深宽比随设计湿润比的增大而增大,这说明设计湿润比对垂直方向运移距离的影响大于对水平方向运移距离的影响,这是由于同一滴头流量不会影响湿润锋在水平方向的扩散速率,但随着设计湿润比增大,灌水时间延长,而土水势梯度又随时间推移逐渐减小,在重力势和基质势共同作用下,土壤水分在垂直方向运移速率增大。因此滴头流量主要影响湿润体的水平运移距离,而设计湿润比主要影响湿润体的垂直运移距离。

表3 不同设计湿润比下滴头流量对湿润体深宽比的影响
3.2设计湿润比对土壤水分分布的影响
设计湿润比的选取对滴灌的灌溉效果有很大影响,图5为灌水结束时,4.1 L·h-1滴头流量、不同设计湿润比下的土壤水分分布情况。从图中可以得出,入渗所形成的湿润体剖面均为1/4椭圆形,随设计湿润比增大,入渗的水平和垂直距离逐渐变大,湿润体体积也相应变大。
设计湿润比越大,湿润体内高含水区(含水率>0.410 cm3·cm-3)半径也越大,例如设计湿润比为40%时,高含水区表层半径为13 cm,而当设计湿润比为80%时,高含水区表层半径达到16 cm;设计湿润比逐渐增大时,湿润体内的平均含水率也依次增大,分别为0.251、0.256、0.262、0.268、0.272 cm3·cm-3,这是由于随着湿润比增大,虽然灌水量变大,但湿润体积也会相应增大,导致湿润体内的平均含水率变化较小。因此,对含水率值无太大要求的情况下,适当地减小设计湿润比,可以达到节水效果,而且几乎不会影响湿润体内的平均含水率大小。
3.3滴头流量对土壤水分分布的影响
滴头流量影响湿润体的大小、形状和土壤水分分布的不均匀程度,将对作物生长产生影响[17]。图6为灌水结束时设计湿润比为60%、不同滴头流量下湿润体内的含水率分布情况,图为湿润体的1/4剖面。
由图6可以看出滴头流量不同时,湿润体大小随滴头流量增大有小幅度的增加。以滴头流量分别为2.2 L·h-1和4.1 L·h-1为例,滴头流量为2.2 L·h-1时实际湿润比为53.87%,而滴头流量为4.1 L·h-1时实际湿润比为57.45%,增长幅度仅为6.65%;湿润体内高含水区表层半径随滴头流量增大而增大,滴头流量逐渐增大时,湿润体内含水率高于0.410 cm3·cm-3的湿润半径分别为11、13、15、16 cm,这是因为设计湿润比相同时,滴头流量越大,灌水时间越短,地表附近的灌水无法及时下渗,形成积水区的范围也会变大,湿润体内的高含水区的范围也相应增大;由于湿润体大小随滴头流量的增大而增大,因此在设计湿润比相同情况下,滴头流量的增大反而会减小湿润体内的平均含水率,从而有可能在滴头流量较大时,湿润体内的含水率无法满足作物的生长需求。
4 结 论
本文根据非饱和土壤水动力学理论和单点源滴灌条件下土壤水分运移特征,按照试验条件设定边界,建立了单点源滴灌条件下土壤水分运动数学模型,并用商业化HYDRUS-3D软件对模型进行了数值求解。通过对3种设计湿润比、2种流量条件下滴灌土壤水分随时间变化规律的模拟值与实测值进行对比可知:
1) 灌水结束时,观测点处模拟与实测含水率的相对误差均在10%以内;实测与模拟湿润比的相对误差变幅为4.75%~11.78%,总体上模拟结果可以很好地代表实测结果,表明所建模型可用于对实际入渗特性的模拟计算。
2) 滴头流量对湿润锋水平运移距离的影响较大,设计湿润比主要影响湿润锋在垂直方向的运移距离;相同滴头流量(4 L·h-1)时,设计湿润比越大,湿润体内平均含水率越大,且湿润体内高含水区(含水率>0.410 cm3·cm-3)半径也越大;设计湿润比相同(60%),滴头流量不同时,湿润体大小随滴头流量


图5 设计湿润比对土壤水分分布的影响
图6滴头流量对土壤水分分布的影响(模拟)
Fig.6Effects of dripper discharge on soil water distribution (simulation)
增大有小幅度增加,湿润体内含水率高于0.410 cm3·cm-3的半径随滴头流量的增大而增大,但是滴头流量增大反而会降低湿润体内的平均含水率。
实际指导灌溉时,应结合作物根区分布情况,合理地选择滴头流量和设计湿润比,使水分不至于造成无效蒸发和深层渗漏,例如滴灌条件下种植棉花、蔬菜等经济作物,根系在垂直方向主要分布在0~30 cm土层,在水平方向是由作物植株处向两侧逐渐减小,适宜选择较小的设计湿润比和较大的滴头流量,既不会造成深层渗漏,也可以达到很好的湿润效果。
[1]张振华,蔡焕杰,郭永昌,等.滴灌土壤湿润体影响因素的实验研究[J].农业工程学报,2002,18(2):17-20.
[2]李道西,代小平,冯江,等.滴头流量和灌水量对滴灌土壤水分运动的影响[J].节水灌溉,2012,(2):13-15.
[3]Cote C M, Bristow K L, Charlesworth P B, et al. Analysis of soil wetting and solute transport in subsurface trickle irrigation[J]. Irrigation Science, 2003,22(3/4):143-156.
[4]A. A. Siyal, T. H. Skaggs. Measured and simulated soil wetting patterns under porous clay pipe sub-surface irrigation[J]. Agricultural water Management, 2008,96(6):893-904.
[5]张林,吴普特,朱德兰,等.多点源滴灌条件下土壤水分运移模拟试验研究[J].排灌机械工程学报,2012,30(2):237-243.[6]魏群,费良军.地表滴灌点源入渗土壤水分运动的模拟研究[J].广东水利水电,2012,(z1):7-10,15.
[7]傅琳,董文楚,郑耀泉.微灌工程技术指南[M].北京:水利电力出版社,1988:96-100.
[8]Keller J, Karmeli D. Trickle irrigation design parameters[J]. Transaction of the ASAE, 1974,17(4):678-684.
[9]雷廷武,郑耀泉,聂光镛.滴灌湿润比的有理设计方法及应用[J].农业工程学报,1992,8(1):23-34.
[10]雷廷武.滴灌湿润比的解析设计[J].水利学报,1994,(1):1-9. [11]晏清洪,王伟,任德新,等.滴灌湿润比对成龄库尔勒香梨生长及耗水规律的影响[J].干旱地区农业研究,2011,29(1):7-13.[12]李光永,郑耀泉,曾德超,等.地埋点源非饱和土壤水运动的数值模拟[J].水利学报,1996,27(11):47-56.
[13]张林,吴普特,范兴科.多点源滴灌条件下土壤水分运动的数值模拟[J].农业工程学报,2010,26(9):40-45.
[14]李久生,张建君,饶敏杰.滴灌施肥灌溉的水氮运移数学模拟及试验验证[J].水利学报,2005,36(8):932-938.
[15]Liping Pang, Murray E Close, James P.C Watt, et al. Simulation of picloram, atrazine, and simazine leaching through two New Zealand soils and into ground water using HYDRUS-2D[J]. Journal of Contaminant Hydrology, 2000,44(1):19-46.
[16]Prit Pal Singh Lubana, N.K. Narda. Soil water dynamics model for trickle irrigated tomatoes[J]. Agricultural Water Management, 1998,37(2):145-161.
[17]李明思,康绍忠,孙海燕.点源滴灌滴头流量与湿润体关系研究[J].农业工程学报,2006,22(4):32-35.
Simulation of soil infiltration characteristics under different wetted soil percentage
WANG Ping, HU Xiao-tao, WANG Wen-e
(KeyLaboratoryofAgriculturalSoilandWaterEngineeringinAridandSemiaridAreas,MinistryofEducation,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)
Designed wetted percentage and dripper discharge are two important parameters in the design of drip irrigation system, affecting the size of wetted body and growth status of plant. With the aim of elucidating the influence of dripper discharge and thereby designing wetted percentage according to soil moisture migration and wetting soil characteristic, this paper based on the theory of unsaturated dynamics and the characteristics of soil moisture transfer under drip irrigation, and established a model of soil water movement, HYDRUS-3D software, to solve the soil infiltration model under different wetted soil percentage. The contrast of measured and simulated values showed that at the end of irrigation, the relative error between simulated and measured values of each observation point were less than 10%, and those for wetted soil percentage were 4.75%~11.78%. By simulating the wetted soil moisture migration under different condition using the established model, we obtained the rule of wetting body characteristics. Dripper discharge mainly affected the migration distance in horizontal direction, design wetted soil percentage had a greater influence on vertical direction. When the dipper discharge is the same, the larger the design wetted soil percentage, the greater the average moisture content in wetted body and the bigger radius of high water zone (water content>0.410 cm3·cm-3). When the design wetted percentage was the same, the radius of high water cut in wetted body increased as the dripper discharge increased.
drip irrigation; wetted percentage; infiltration characteristics; soil water content; numerical simulation
1000-7601(2016)04-0006-06
10.7606/j.issn.1000-7601.2016.04.02
2015-09-10
国家自然科学基金项目(51179163)
王平(1989—),女,河北沧州人,硕士研究生,主要从事节水灌溉原理与新技术研究。 E-mail:1092443775@qq.com。
胡笑涛(1972—),男,博士,教授,主要从事节水灌溉理论与新技术研究。 E-mail:huxiaotao11@nwsuaf.edu.cn。
doi:10.7606/j.issn.1000-7601.2016.04.02
S275.6
A
文章编号:1000-7601(2016)04-0006-06
收稿日期:2015-09-10
基金项目:国家自然科学基金项目(51179163)
作者简介:王平(1989—),女,河北沧州人,硕士研究生,主要从事节水灌溉原理与新技术研究。 E-mail:1092443775@qq.com。
通信作者:胡笑涛(1972—),男,博士,教授,主要从事节水灌溉理论与新技术研究。 E-mail:huxiaotao11@nwsuaf.edu.cn。
