南昌朝阳大桥波形钢腹板抗剪力学性能分析

戴杰吉， 余天庆， 刘耀东， 张若钢

(1 湖北工业大学土木工程与建筑学院， 湖北 武汉　430068；2 中铁大桥科学研究院有限公司，湖北 武汉 430034)



南昌朝阳大桥波形钢腹板抗剪力学性能分析

戴杰吉1， 余天庆1， 刘耀东1， 张若钢2

(1 湖北工业大学土木工程与建筑学院， 湖北 武汉430068；2 中铁大桥科学研究院有限公司，湖北 武汉 430034)

利用MIDAS FEA建立朝阳大桥有限元仿真模型，并对比验证了模型的适用性，通过对有限元模型的分析，验证了波形钢腹板的“手风琴”结构效应及拟平面假设，得出波形钢腹板剪力传递能力与混凝土顶板和底板剪力的绝对值大小成反比，并且当剪力传递能力达到一定范围后，波形刚腹板板厚增加并不会很大程度提高剪力传递能力，可将剪力传递能力范围在60%～80%作为波形钢腹板桥梁设计的参考依据。

波形钢腹板；拟平面假设；剪力传递能力

1　工程概况

朝阳大桥为六塔单索面斜拉桥，主塔为钢筋混凝土结构，主梁采用波形钢腹板PC组合箱梁，斜拉索为扇形布置，每塔共2×9对索，跨径布置为75 m+5×150 m+75 m，桥面宽度为37 m，结构体系为塔梁固结、梁墩分离，梁底设支座的结构体系，其结构形式及主梁断面见图1、图2。

图 1　主桥总体布置图

图 2　A-A截面测点位置及编号

2　荷载试验及有限元模型

2.1荷载试验

朝阳大桥设计为双向8车道，通车前对桥梁进行了全桥静载荷载试验，主梁部分监测的数据主要包括竖向挠度、混凝土顶板和底板纵向应变、波纹钢腹板剪应力。为了验证有限元模型的适用性，考虑实测数据的完整性，选取荷载试验中一个工况实测数据与有限元计算值进行对比。该工况为主塔附近最大负弯矩对称加载，沿主梁纵向中心线对称布置4排30 t加载车共30辆，其中1～3排每排对称布置共8辆，4排对称布置共6辆，其控制截面A-A及主梁测点布置见图1、图2。

2.2有限元模型

采用有限元分析软件MIDAS FEA建立分析模型，其中主塔、混凝土顶板和底板采用3D实体单元，波形钢腹板采用2D板单元，斜拉锁采用1D桁架单元进行模拟，考虑荷载试验工况的影响范围及作用位置，只建立19#墩、18#墩桥跨模型(图1方框范围)，提取已建好的MIDAS Civil杆系单元全桥模型的边界条件施加到FEA模型断面上，实测数据只考虑各测点在工况荷载作用下的增量变化，为了真实的进行模拟，本文分析也只考虑工况荷载作用下的增量对结构的影响。

2.3实测值与有限元计算值

提取有限元模型中各测点实测值与计算值进行对比，对比结果见图3、表1和表2。从对比结果中可以看出挠度实测值与计算值的线性几乎重合，应力、应变结果相差不大，趋势一致，有限元模型较真实地模拟了实际情况。

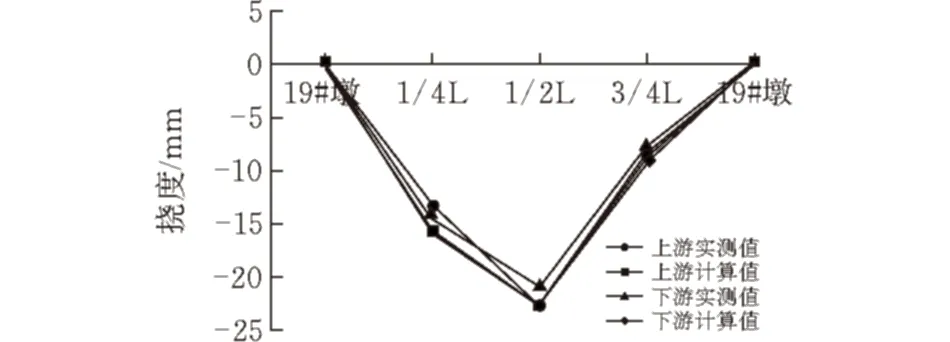
图 3　试验工况主梁挠度

表 1　A-A截面试验工况应变值

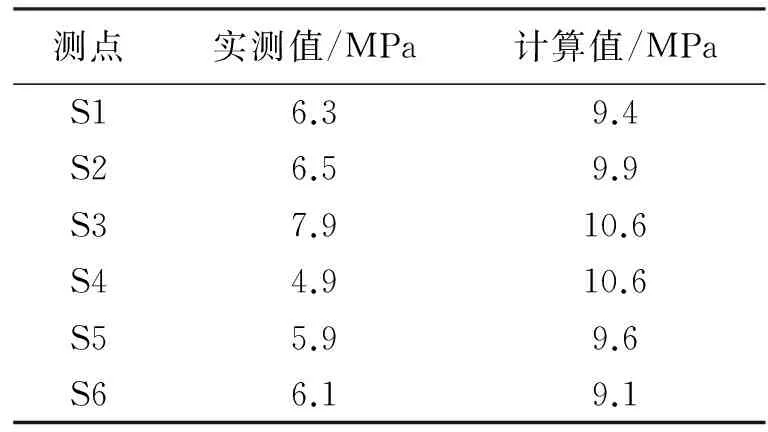
表 2　A-A截面试验工况剪应力值

3　抗剪力学性能分析

3.1波形钢腹板拟平面假定

“手风琴”结构效应是波形钢腹板所具有的独特特点，使其主要承受剪力、基本不承受弯矩[1]，根据这一效应，可以认为结构上作用的弯矩主要由混凝土顶板和底板承担，因此可以认为：混凝土顶板和底板的纵向正应变相对波形钢腹板会大很多，而波形钢腹板沿高度范围内的应变值接近于零[2]。通过施加前文中的荷载试验工况，提取控制截面A-A的应变数据对这一假定进行了验证。

考虑结构及荷载的对称性，仅提取主梁断面一侧应变值，沿A-A断面腹板高度方向10等分提取腹板应变值、3等分提取混凝土顶板和底板应变值，结果见图4、图5、图6。

图 4　FB1处正应变沿梁高分布图

图 5　FB2处正应变沿梁高分布图

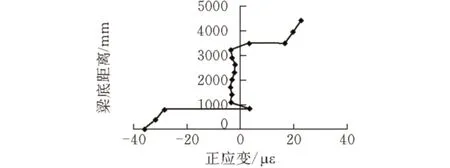
图 6　FB3处正应变沿梁高分布图

从图4、图5和图6可以看出，混凝土顶、底板应变明显大于腹板应变，并且腹板应变数值较小，在混凝土顶、底板和腹板的交界处还发生了明显的应变突变现象，这些都验证了波形钢腹板所特有的“手风琴”结构特点产生的力学性能，同时，如果去掉提取的波形钢腹板的应变点，将混凝土顶板和底板的6个点相连，可以近似构成一条虚拟平面[3]，这也验证了波形钢腹板组合箱梁的拟平面假定。

3.2剪力分析

波形钢腹板所承担的剪力可以根据其剪应力与波形钢腹板截面面积的乘积得到[4]，因此可以通过此方法计算出波形钢腹板的剪力，并与混凝土顶板和底板所承担的剪力进行比较，计算出波形钢腹板的剪力传递能力[5]，即波形钢腹板所承担剪力占腹板及混凝土顶板和底板共同承担剪力的比重。通过剪力传递能力这一指标来分析混凝土顶板和底板所承担剪力大小与钢腹板剪力传递能力之间的关系，以及波形钢腹板板厚对混凝土剪力传递能力的影响。

该桥每跨为9个标准节段悬臂浇筑施工而成，标准节段构造相同，为了得到不同混凝土顶板和底板承担的剪力值，选取1-9号节段相同位置断面共18个，断面名称从左到右分别编号为L1-1～L9-9、R9-9～R1-1(图1)。

FEA中可以直接提取断面的混凝土顶板和底板剪力值，但是每个断面6道腹板所承担的剪力值在FEA中无法直接提取，可以通过提取各道腹板断面沿腹板高度方向10个等分点的剪应力值，图7为L1-1断面腹板剪应力沿高度分布规律，其他截面规律相同，可以看出腹板剪应力沿高度方向基本相等[6]，因此取这10个点的剪应力平均值即为腹板断面剪应力，再乘以相应的腹板断面面积，即得到每道腹板所承担的剪力值，将6道腹板的剪力值求出并求和，即为该断面6道波形钢腹板所承担的剪力总值。在此不作详细计算，计算结果见表3。

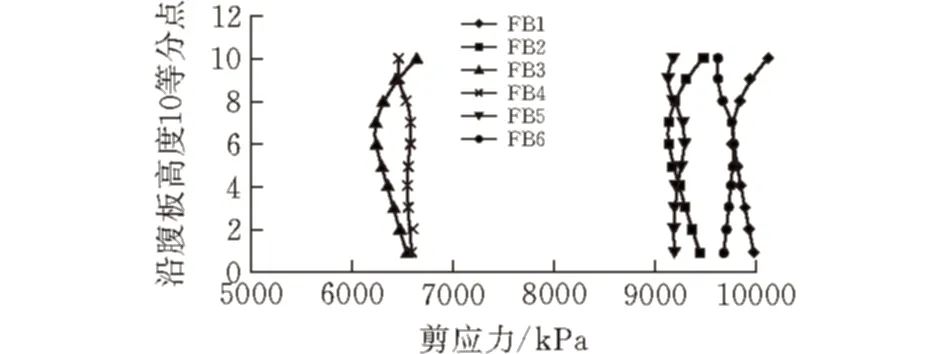
图 7　L1-1断面腹板剪应力沿高度分布图

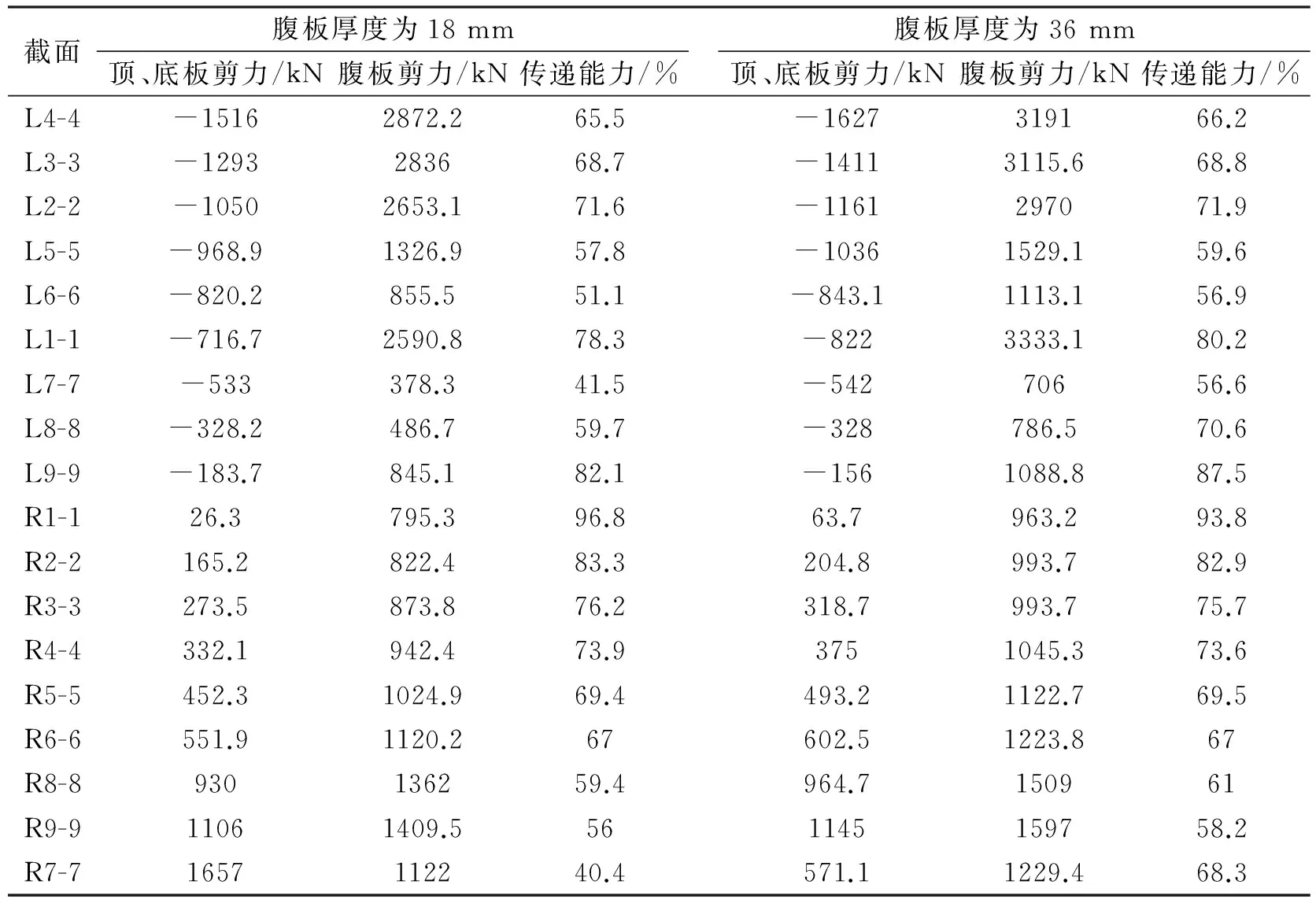
表 3　剪力传递能力计算表

为了便于观察波箱钢腹板剪力传递能力的规律，表中数据按照混凝土顶板和底板剪力值进行排序，混凝土承担剪力与剪力传递能力对比见图8。

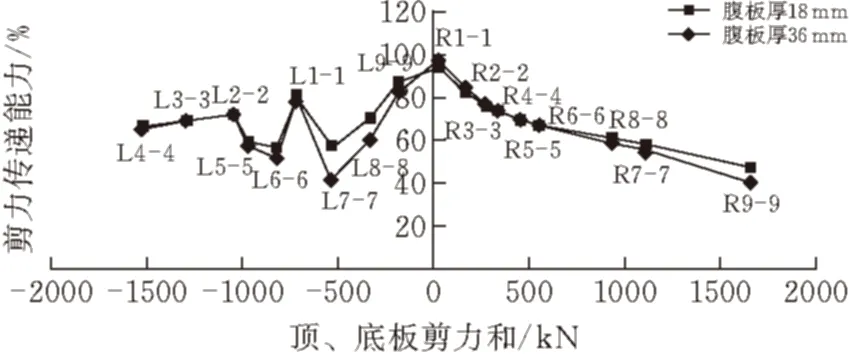
图 8　剪力传递能力对比图

从图8纵向看，左边负剪力区间，L4-4、3-3、2-2、1-1、9-9截面混凝土顶板和底板剪力的绝对值依次从大到小，剪力传递能力依次从小到大；右边正剪力区间，很明显的可以看出混凝土顶板和底板剪力值越大，波形钢腹板剪力传递能力越小。从两区间总体上看，混凝土顶板和底板剪力的绝对值越大，波形钢腹板剪力传递能力越小。但是从图中也可以看到，在L5-5、6-6、7-7截面却并没有这样的规律，这是因为这3个截面正好处于车辆集中荷载作用处，其混凝土顶板和底板剪力额外增大，从而导致波形钢判剪力传递能力迅速下降，所以其实质依然是混凝土顶板和底板剪力增大，波形钢腹板剪力传递能力减弱。因此在设计波形钢腹板桥梁时，剪力较小的位置也需要特别注意，这些位置可能会因为剪力传递能力过大导致腹板承受的剪力过大而破坏。

从图8竖向看，随着波形钢腹板的板厚增加一倍，其剪力传递能力除了R1-1以外，均增大， R1-1处之所以减小，也是因为混凝土顶板和底板承担的剪力值变大，从表3横向上看，依旧可以发现该规律。此外，腹板厚度增加一倍，但是剪力传递能力并没有太大的提高，因此，对于波形钢腹板来说，不是板厚越大越好，在设计时应该考虑一个合适的范围，从表中可以看出波形钢腹板剪力传递能力在40%～96%之间，其中63%的数据分布在60%～80%之间，因此设计该类桥梁的时候，可以考虑将剪力传递能力范围设在60%～80%。

4　结论

1)建立了朝阳大桥实体有限元分析模型，通过与实测数据对比，得出有限元模型能够较真实地反应结构实际情况。

2)通过分析沿梁高方向腹板、混凝土顶板和底板的应变变化规律，发现腹板正应变明显小于混凝土顶板和底板正应变，并且在波形钢腹板与混凝土顶板和底板的结合处发生了应变突变，这证明了波形钢腹板“手风琴”的结构特点，即主要承担剪力、基本不承担弯矩。同时混凝土顶板和底板的正应变虽然在与腹板结合处发生了突变，但是混凝土顶板和底板沿梁高方向应变依然呈线性分布，满足拟平面假定。

3)通过选取18个不同的截面，分析波形钢腹板的剪力传递能力，可以得出波形钢腹板的剪力传递能力与混凝土顶板和底板所承担剪力的绝对值大小成反比，因此在设计波形钢腹板桥梁时，不可忽视这一点：混凝土顶板和底板剪力较小可能会导致波形钢腹板因剪力传递能力过大而承担剪力过大导致破坏。

4)通过对比发现，波形钢腹板的剪力传递能力与波形钢腹板板厚并不成正比，建议剪力传递能力在60%～80%之间，作为波形钢腹板桥梁设计的一个参考依据。

[1]乔晋姿，祝兵.波形钢腹板PC组合箱梁发展综述及受力分析[J].四川建筑科学研究，2008，34(4):49-52.

[2]Elgaaly M，A Seshadri， Hamilton R W.Bending strength of steel beams with corrugated webs[J].Structure Engineering，1997，123(6):772-782.

[3]吴文清，叶见曙，万水.波形钢腹板-混凝土组合箱梁截面变形的拟平截面假定及其应用研究[J].工程力学，2005，22(5):177-180.

[4]周绪红，孔祥福，侯健，等.波形钢腹板组合箱梁的抗剪受力性能[J].中国公路学报，2007，20(2):77-82.

[5]李杰,武海鹏,陈淮，等.波形钢腹板变截面连续体系梁桥钢腹板承剪分析[J].桥梁建设，2015，(1):79-84.

[6]刘磊，钱冬生.波纹钢腹板的受力行为[J].铁道学报，2000，22(z1):53-56.

[责任编校： 张岩芳]

An Analysis on the Shear Mechanics Property of Corrugated Steel Webs in Nanchang Chaoyang Bridge

DAI Jieji1，YU Tianqing1，LIU Yaodong1，ZHANG Ruogang2

(1SchoolofCivilEngineeringandArchitecture，HubeiUniv.ofTech.，Wuhan430068，China；2BridgeScienceResearchInstituteLtd.，ChinaRailwayMajorEngineeringGroup，Wuhan430034，China)

Finite element simulation model of Chaoyang Bridge was established with MIDAS FEA, and the applicability of model was compared and verified. The “accordion” structure effect and quasi plane assumption of corrugated steel webs were testified through the analysis of finite element model, and it was concluded that the shear force transmission capacity is inversely proportional to the absolute value of the concrete roof and bottom shear force. Meanwhile, when the shear force transmission capacity reaches a certain range, it may not be improved greatly by increasing the thickness of corrugated steel webs, and the shear force range between 60% to 80% can be taken as the design reference of corrugated steel web bridge.

corrugated steel webs; quasi plane assumption; shear force transmission capacity

2015-09-28

戴杰吉(1990-)， 男， 湖北荆州人，湖北工业大学硕士研究生，研究方向为桥梁病害监测与修补加固

1003-4684(2016)04-0113-04

TU312

A