基于混沌优化的约束优化问题求解方法实现

刘道文

(许昌学院 电气信息工程学院，河南 许昌 461000)



基于混沌优化的约束优化问题求解方法实现

刘道文

(许昌学院 电气信息工程学院，河南 许昌 461000)

在分析混沌序列遍历性基础上，将混沌序列映射到多极点目标函数的搜索区间搜索全局最优解.研究混沌优化算法的一般步骤，设计和实现混沌优化算法，并将混沌优化算法应用于带约束条件的最优化求解问题.仿真结果表明，混沌优化算法具有较好的全局搜索最优解能力，验证了其在约束优化问题求解上的可行性和有效性.

混沌优化；约束条件；全局搜索；遍历性

最优化问题求解是数学与计算技术中一种求极值的方法，为工程中实际问题的解决提供了理论基础和方法支持[1].科学和工程实践领域中的许多优化问题一般都可以归结成为求解一个带有约束条件的函数优化问题，但已有的许多约束优化问题求解算法是基于梯度的概念，一般只能保证求到局部最优解[2].混沌优化作为一种全局优化算法能够较好地避免陷入局部极小值的问题，能够在决策问题状态空间中搜索到全局最优解，且与初始点选择的关联度弱，其基本思想是将混沌序列线性映射到优化变量区间，并利用混沌变量对目标函数全局极大值进行搜索[3].

一般地，科学研究和工程实践中大多数的带有约束条件问题的处理可转化成为对一个带有约束条件函数的优化.通常，一个约束优化问题可以描述如下[4]：

(1)

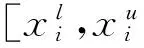
1　混沌遍历特性

混沌是指确定性非线性系统中存在的一种貌似无规则、随机的现象，具有遍历性、随机性和内在规律性，能在一定范围内按其内在规律不重复地遍历所有状态[4].因此，在充分长的时间区间里，随着时间的推移，混沌运动将遍历状态空间上的每一个点，如图1所示.混沌的遍历性是利用混沌序列进行全局最优解搜索的理论基础，与随机过程不同的是，混沌在看似无规则的运动过程中蕴含着自身的内在演化规律，是由确定性的内在物理规律引起的，是源于内在特性的外在表现，混沌的关联维数曲线在一定范围内趋于收敛，而随机噪声的关联维数趋于发散，如图2所示.本文以Logistic混沌时间序列为例验证混沌的遍历特性，并利用关联维数分析Logistic混沌时间序列蕴含的内在规律，证明混沌时间序列与均匀分布的随机过程本质上的不同，为混沌优化提供理论支持.

图1　混沌分岔图和时序图

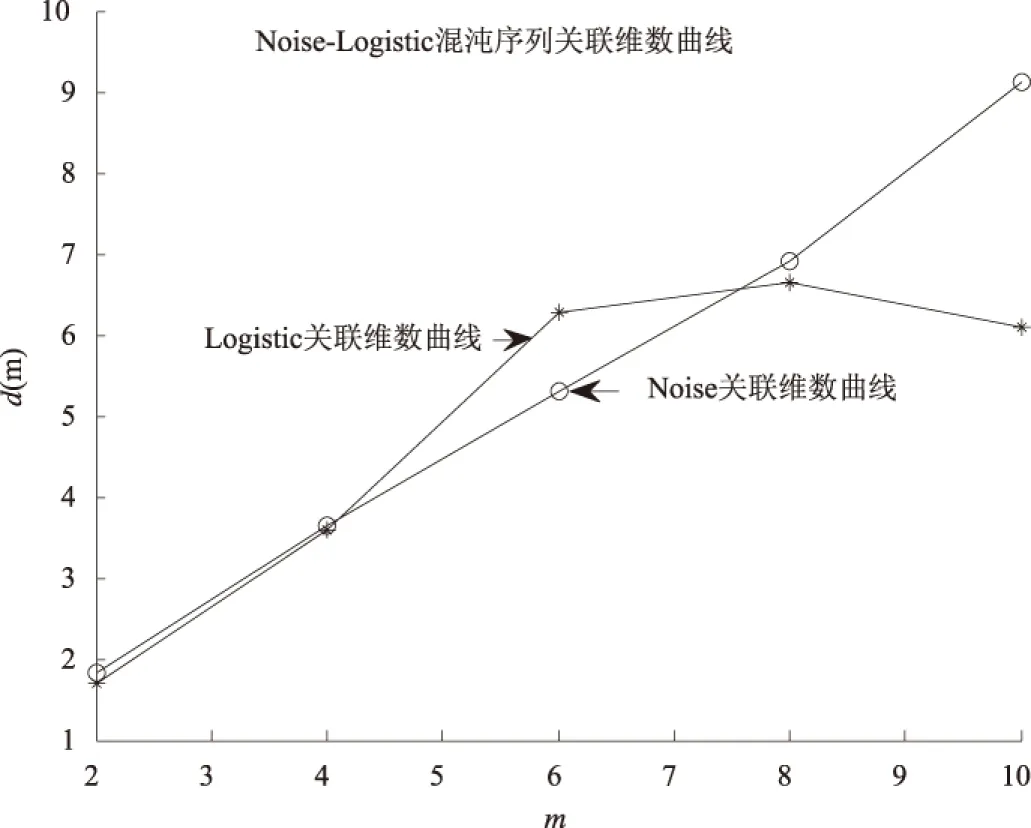
图2　混沌与噪声关联维数曲线

2　混沌优化算法

本文采用Logistic混沌变量对目标函数进行全局最优化搜索，对连续对象的全局极小值优化问题[5，6]：

minf(xi)(s.t.xi∈[ai,bi],i=1,2,…n).

(2)

(3)

其中ci,di为常数.

第四步，经过第3步的若干次搜索f*保持不变，则按(4)式进行第二次载波.

(4)

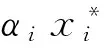
第六步，如果满足终止条件则终止搜索并输出最优解，反之则返回第五步继续搜索.

3　算法实现与仿真

针对多极点函数，利用混沌优化算法在整个解空间内搜索全局最优值，本文选择(5)式的多极点函数作为目标函数，如图3所示，设计与实现混沌优化算法并仿真计算其全局最优值.从图3可以看出该函数在定义域范围内有三个局部极值，但其只有一个全局最优解.对于多极点目标函数的最优求解问题，利用传统优化算法求解时初始点的选择对最优化结果有较大的影响，很容易陷入局部极值而无法得到全局最优解，而利用混沌优化可在整个解空间内遍历各个点上的值并能搜索到全局最优解[9].

(5)

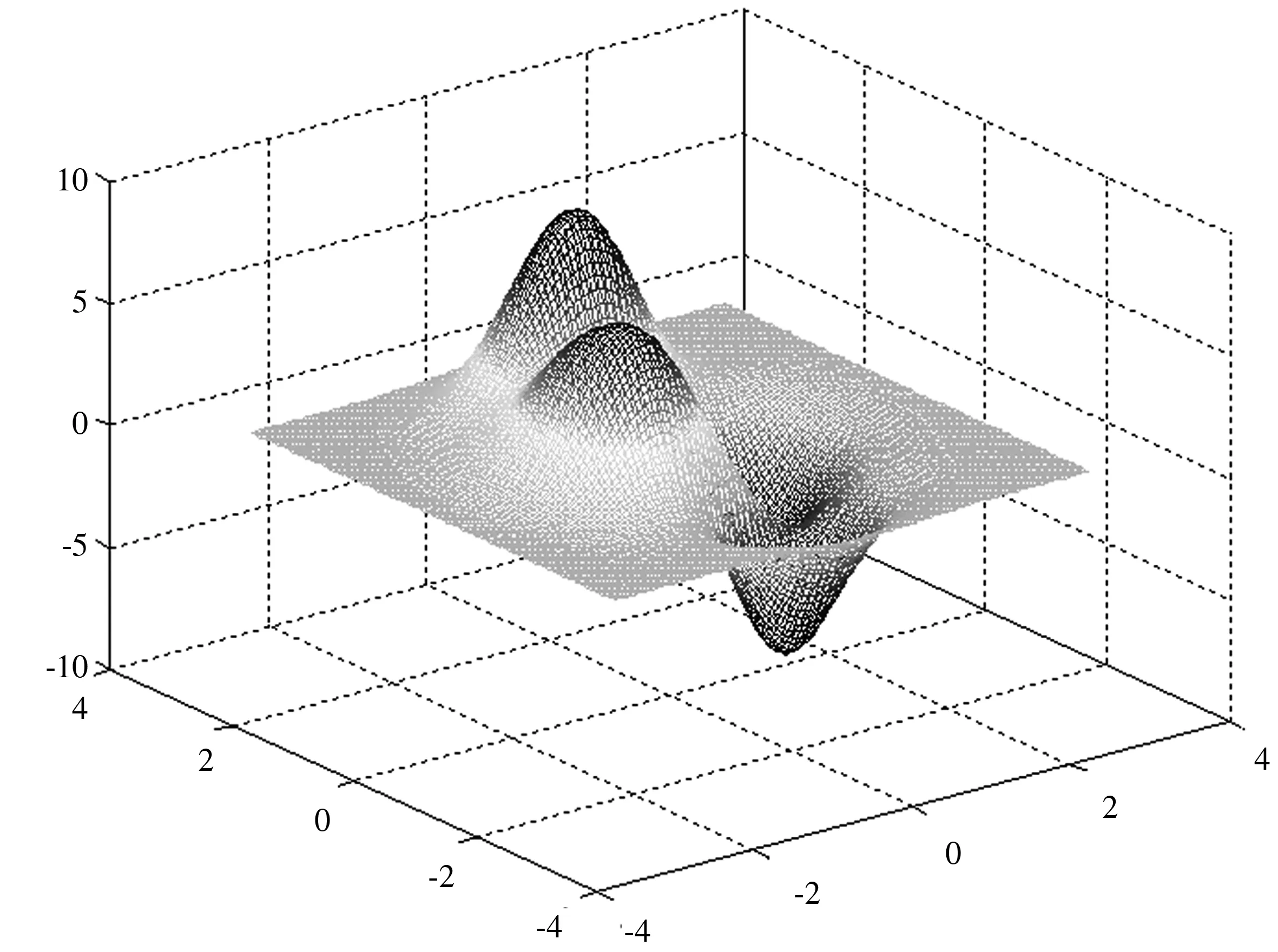
图3　多极值目标函数

3.1目标函数与约束条件

在求解最优化问题时，对于maxf(x,y)可以转换成minc-f(x,y),∀c∈R，在算法实现时具体选择maxf(x,y)还是minc-f(x,y)可根据目标函数的特点或计算要求而定[10].为了提高优化算法程序的通用性和可靠性，在Matlab中可将目标函数设计成一个独立的代码模块并命名为myfun.m，实现(5)式目标函数的Matlab代码如下：

function myfun = myfun(x1,x2)

myfun=1-3 *(1 - x1).^2 .*exp(-x1.^2-(x2+1).^2)-10*(x1./5+x1.^3-x2.^5).*exp(-x1.^2-x2.^2)-1/3*exp(-(x1+1).^2-x2.^2);

end

同样，在Matlab中将目标函数的约束关系也设计成一个独立的代码模块并命名为constraint.m，实现(5)式目标函数约束关系的Matlab代码如下：

function constraint=constraint(x1,x2)

if x1>=-3 && x1<=3 && x2>=-3 && x2<=3

constraint=1;

else

constraint=0;

end

3.2算法实现

利用混沌优化算法处理约束优化求解问题是基于混沌在能够充分长的时间内遍历解空间中的各个状态点，其思路是将混沌序列映射到约束条件空间来求解目标函数的最优解[11]，优化过程主要包括混沌变量产生和调制、利用混沌序列值求解目标函数、最优解判定、二次优化等步骤，算法实现的主要步骤如下：

①用0-1均匀分布的随机序列初始化变量向量X，将其调制到定义域空间并赋给向量Temp_X；

②将Temp_X向量中的数值代入constraint函数中用以判定是否满足约束条件，满足约束条件则继续执行，否则结束本次执行；

③在满足约束条件的情况下，利用初始化的变量向量计算目标函数的结果Max_F，并将其作为最优结果的初始值；

④利用Logistic迭代产生Logistic混沌序列，将每次迭代得到的混沌序列值代入目标函数中计算其结果保存于变量Temp_F，并与Max_F进行比较，若Temp_F>Max_F，则将当前的混沌序列值赋给向量Max_X、Temp_F赋给Max_F；

⑤判定当前最优解是否满足要求，满足要求则结束，否则进行二次混沌优化；

⑥重新产生混沌序列用来初始化向量X，并在第一次混沌优化得到的搜索空间的基础上进一步缩小搜索范围寻找最优解，并判定所得到的最优解是否满足要求，满足要求就结束执行，否则重新进行下一轮的优化求解过程，直至得到满足要求的最优解，算法实现的程序流程图如图4所示.

利用上述的算法流程，针对(5)式的多极值目标函数随机进行了10次最优化仿真计算，得到的最优解和对应的目标函数值如表1所示.

图4　算法实现流程图

4　结语

混沌优化算法作为一种全局优化算法能够遍历目标函数解空间上的各个点，并较好地搜索出目标函数的全局极值，仿真计算表明，混沌优化算法在约束优化问题求解上具有可行性和有效性.

表1　仿真计算结果

[1]赵晓芬.求解约束优化问题的差分演化算法[D].西安:西安电子科技大学,2012.

[2]林丹,李敏强,寇纪凇.基于遗传算法求解约束优化问题的一种算法[J].软件学报,2001,12(4):628-629.

[3]张彤,王宏伟.变尺度混沌优化方法及其应用[J].控制与决策,1999,14(3):285-287

[4]张利彪,周春光,刘小华,等.求解约束优化问题的一种新的进化算法[J].吉林大学学报,2004,42(4):534-535.

[5]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.

[6]胡行华.混沌优化算法的研究与应用[D].阜新:辽宁工程技术大学,2008.

[7]李祥飞.混沌优化理论在控制系统设计中的研究[D].长沙：中南大学，2003.

[8]许海平，朱奕，张彤，等.变尺度混沌优化方法在电站经济运行中的应用[J].哈尔滨工业大学学报，2000，32(4)：55-58.

[9]张双乐，李鹏，陈超，等.基于改进变尺度混沌优化算法的微网优化运行[J].电力自动化设备，2013，33(1)：71-73.

[10]王爽心，韩芳，朱衡君.基于改进变尺度混沌优化方法的经济负荷分配[J].中国电机工程学报，2005，25(24)：90-95.

[11]刘丽军，李捷，蔡金锭，等.基于强引导粒子群和混沌优化的电力系统无功优化[J].电力自动化设备，2010，30(4)：71-75.

责任编辑：赵秋宇

Realization of Solving Constrained Optimization Problems Based on Chaos Optimization Method

LIU Dao-wen

(SchoolofElectricalEngineering,XuchangUniversity,Xuchang461000,China)

Based on the analysis of ergodicity of chaotic sequences, We can search global optimal solution that the chaotic sequence is mapped to the search rigion. Studying the general procedure of chaos optimization algorithm, designing and implementing chaos optimization algorithm, we apply the chaos optimization algorithm to the optimization problem with constrained condition. The simulation results prove the chaos optimization algorithm has better global search ability for solving constrained optimization problems and test its feasibility and effectiveness.

chaos optimization; constrained condition; global search; ergodicity

2015-07-20

河南省高校重点科研项目(16A520070);2015年度许昌市科技攻关项目(1502088)

刘道文(1980—)，男，河南罗山人，副教授，硕士，研究方向：混沌理论与应用．

1671-9824(2016)05-0030-05

O241.5

A