基于固有模态的单层球面网壳减震控制
2016-10-18刘怡鹏罗永峰
刘怡鹏, 罗永峰, 相 阳
(同济大学 土木工程学院, 上海 200092)
基于固有模态的单层球面网壳减震控制
刘怡鹏, 罗永峰, 相阳
(同济大学 土木工程学院, 上海 200092)
简要介绍并总结了目前大跨度空间结构多重调频质量阻尼器(MTMD)减震控制的发展过程及研究现状.建立了网壳结构MTMD减震控制系统动力学基本方程并进行解耦分析,进而提出了基于控制特定的固有模态的单层球面网壳结构分布多重调频质量阻尼器(D-MTMD)减震设计方法与步骤.建立了一个单层球面网壳数值模型,分别考虑水平、竖向地震输入两类工况,对不同震动控制方案的网壳采用El Centro波进行时程分析,并对计算结果进行分析对比.计算结果表明,该减震控制方法可以有效减小结构地震响应.同时,根据数值计算结果,总结提出了一些关于减震控制效果优化的建议.
固有模态; 单层球面网壳; 分布多重调频质量阻尼器; 减震控制
虽然结构振动控制技术在土木工程中的应用研究已有近40年的历史,但目前的研究主要集中在多、高层房屋及高耸结构中.而在大跨空间结构的振动控制方面,尤其在实际工程中的应用研究则较少,目前尚处于起步阶段.调频质量阻尼器(TMD)系统在高层及高耸结构振动控制中已被验证为经济有效的手段之一.然而,由于其控制频带窄、自振周期长、安装不便等特点[1-3],在大跨度空间结构中的应用仅仅停留在理论分析方面.
近年来,国内外学者逐渐对TMD在大跨度空间结构振动控制的适用性进行研究.叶继红等[4-5]利用TMD系统对各类网壳结构进行了振动控制分析研究,提出了采用传递函数算法及非线性数学规划方法确定其最优控制参数.胡继军等[6]将TMD应用于网壳的风振控制中,利用提出的TMD影响函数,优化了TMD系统中的一些参数,并对控制模态的干扰问题进行了分析.林勇建等[7]采用频域分析方法对柱面网壳进行了风振响应计算,并对其采用多重调谐质量阻尼器(MTMD)减振控制进行了研究,通过数值分析计算,得到最优总质量比、阻尼比等参数.唐柏鉴[8]提出了“振型分组、多组MTMD分别控制”的控制策略,分析了频宽、阻尼比和质量比的参数影响规律,并用时程分析法检验了该理论的准确性及其减震效果,并结合工程实例对大跨度屋盖结构MTMD减震控制进行研究,提出了网格屋盖结构竖向MTMD的振动控制方程.
日本学者对大跨度空间结构的MTMD减震系统已有较深入的研究,1996年,Yamada[9]对网壳结构TMD振动控制进行了探索性研究,但研究模型比较简单,仅为两节点,自由度数量较少,局限性强.Yoshinaka等[10]通过在大跨度空间结构中分别采用单TMD系统与多调频质量阻尼器(MTMD)系统进行了理论分析和数值计算,并对两者减震效率进行了分析对比.Tsuda等[11]将理论用于实际,提出一种用于大跨度空间结构双向地震控制的振动控制装置BD-TMD ( Bi- Directional- TMD ),并用数值方法进行了振动控制效果验算,得到了满意的效果.Yamakawa等[12]则提出一种概率优化的方法来预估MTMD系统的具体布置参数,并验证了其有效性.总体来说,在大跨度网壳结构TMD振动控制方面研究相对较少,而且仅限于简单模型,对于MTMD在网壳结构中优化配置的方法尚没有一个最优配置方案.
本文根据大跨度网壳结构整体动力响应特性,建立多自由度D-MTMD减震控制系统动力学基本方程,并对方程进行解耦及求解,进而提出一种基于控制结构固有模态的D-MTMD减震控制方案,同时,进行理论分析,进一步对该减震控制方案进行优化.最后,对一单层凯威特球面网壳数值算例进行分析,研究在水平及竖向地震荷载作用下,不同减震控制方案的控制效果,同时验证了本文减震控制方法的有效性及减震效果.
1 大跨度网壳结构MTMD系统运动方程
目前,对于结构MTMD系统的理论研究,将结构简化为一单自由度体系,然后将单个TMD分为多个不同频率的小质量块,以降低单个TMD对地震反应频率的敏感性,组成集中多调频质量阻尼器(C-MTMD)系统[13],对结构进行震动控制,如图1a所示.对于形态复杂的大跨度空间结构,由于自由度众多、频率分布密集、振型形态复杂,宜将多个TMD装置布置于空间结构的不同(特定)位置,组成D-MTMD(分布调频质量阻尼器)系统[14],如图1b所示.其中K0,C0为主结构的刚度和阻尼,Kti,Cti为第i个TMD的刚度和阻尼.
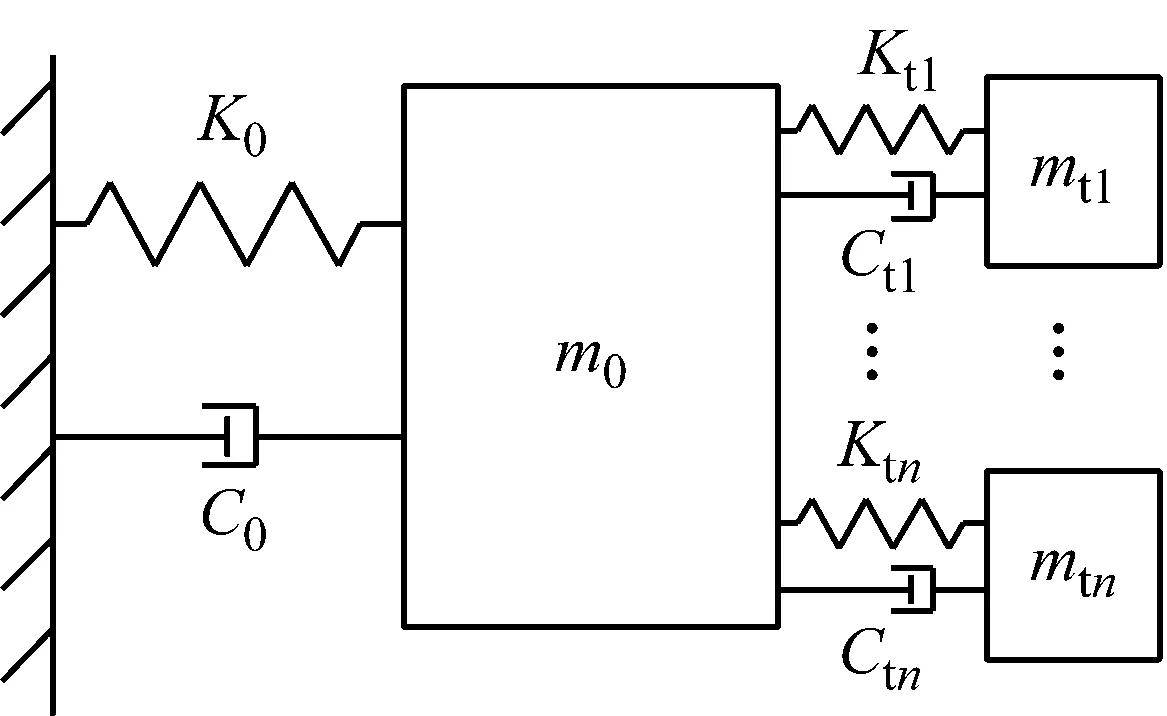
a C-MTMD
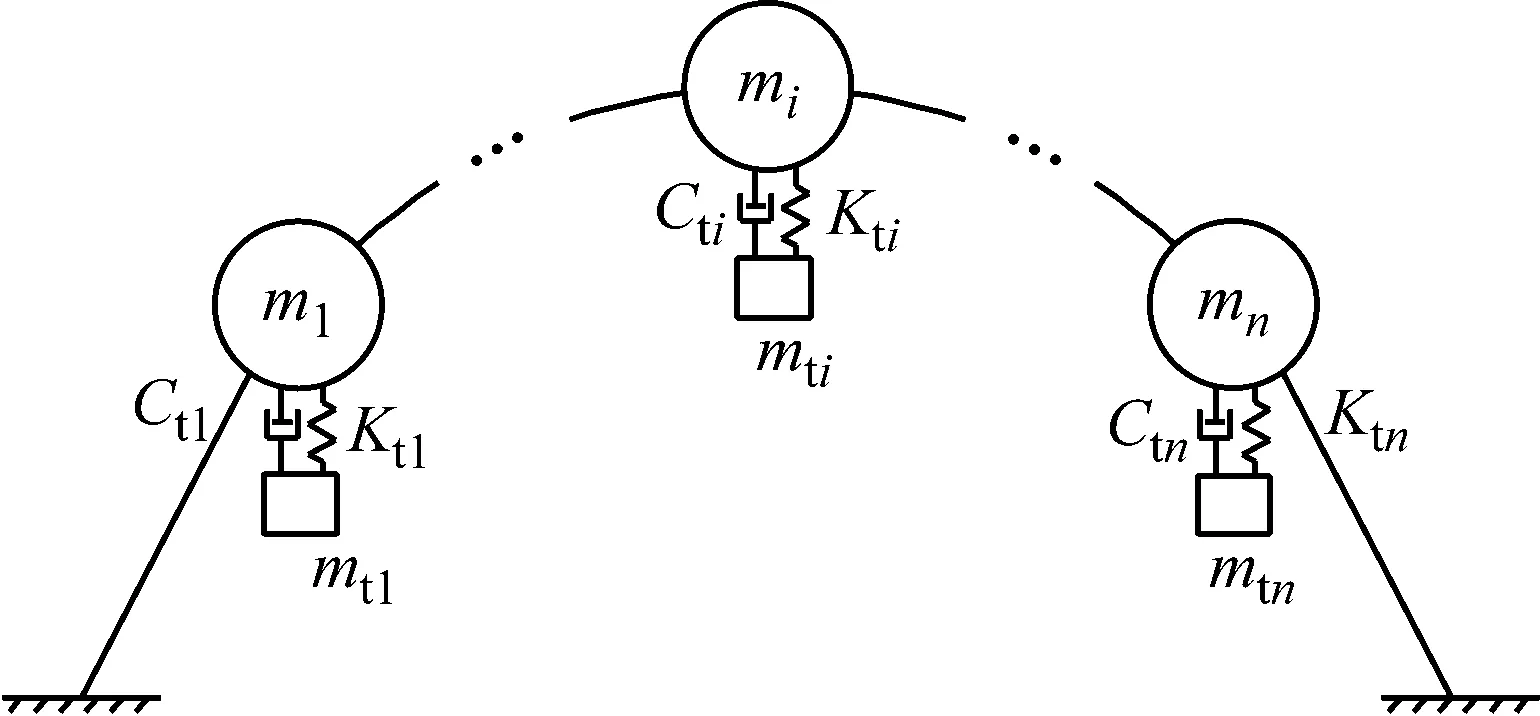
b D-MTMD
针对网壳结构D-MTMD减震控制系统,可建立结构运动学微分方程如下:
(1)
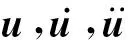
(2)
(3)
同时,可列出MTMD的运动微分方程为

(4)
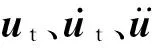
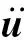
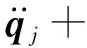
(5)
在线性条件下,由式(5)可知:
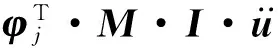


(6)

2 单层球面网壳结构D-MTMD减震设计方法
大跨度单层网壳结构的动力特性与高耸、多高层结构不同,主要体现在:(1)主要贡献振型数量多,频率分布密集,振型耦联效应强;(2) 主要贡献振型的形态复杂,无法简化为单质点TMD减震控制系统;(3)不论水平还是竖直方向地震输入,各质点的位移动力响应主要以竖向(z向)震动为主.
基于网壳结构的动力特性及第1节的理论分析,针对单层网壳结构的减震控制,本文通过归纳与简化,提出以下基于固有模态的单层球面网壳D-MTMD减震控制设计方法与步骤:
(1) 对结构进行动力模态分析,遴选出质量参与系数高的一阶或几阶振型,作为减震设计的控制振型;
(2)确定D-MTMD的总质量mt.考虑到结构可容许的附加荷载,可假设mt=0.05·ms(ms为整个网壳结构质量);

(4)根据TMD振动控制理论,当TMD自振频率与激励频率(工程中一般取所控振型频率)接近时,控制效果最佳.通过调整各TMD刚度kt,使各TMD自振频率ftj与所控振型的频率fsi相等,以达到最佳控制效果;
考虑到D-MTMD装置在实际大跨度网壳结构中的施工与安装,同时由于网壳结构位移动力响应主要以竖向位移为主,故本文仅设置竖向TMD装置即可进行网壳结构减震控制.
3 单层球面网壳D-MTMD减震算例分析
为验证本文基于控制固有模态的单层球面网壳D-MTMD减震控制方法,本节建立一单层凯威特球面网壳数值模型,分别考虑水平方向和竖直方向地震输入两类工况,对控制前后网壳的地震响应进行分析对比,通过数值计算结果说明本文减震控制方法的有效性和适用性.
3.1单层网壳结构模型
K6凯威特单层网壳跨度为40 m,矢高为10 m,矢跨比为1/4,结构杆件均采用Φ150×4钢管,钢材弹性模量为2.06×105MPa,结构阻尼比为0.02,不考虑材料非线性.将网壳结构自重及各类荷载均等效为节点集中质量,每节点为4 000 kg,动力分析中采用集中质量矩阵.杆件均采用铁木辛柯空间梁单元模拟,每根杆件分为两个梁单元.网壳采用周边固定约束支座,约束节点数为36,非约束节点数为91,x、y、z三向总动力自由度数为273,相应地总振型数也为273个.
对该结构进行模态分析,分别统计出水平方向(x向) 和竖直方向(z向)的主要参振振型参数,见表1—2,各振型形态见图2—3.

表1 网壳x向主要振型参数
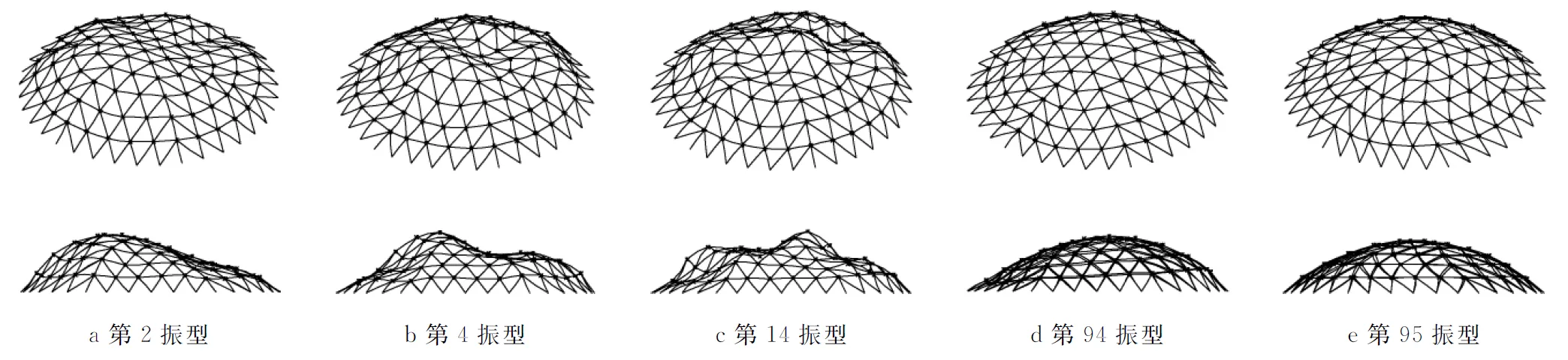
图2 网壳x向主要振型简图

表2 网壳z向主要模态参数

图3 网壳z向主要振型简图
为了了解单层球面网壳D-MTMD减震控制前后的结构动力响应,以下选择一些有代表性的节点位移时程响应和杆件内力时程响应,说明各D-MTMD控制方案的减震效果.图4为所关注的节点和杆件所在位置示意图.
3.2水平地震减震控制分析
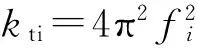
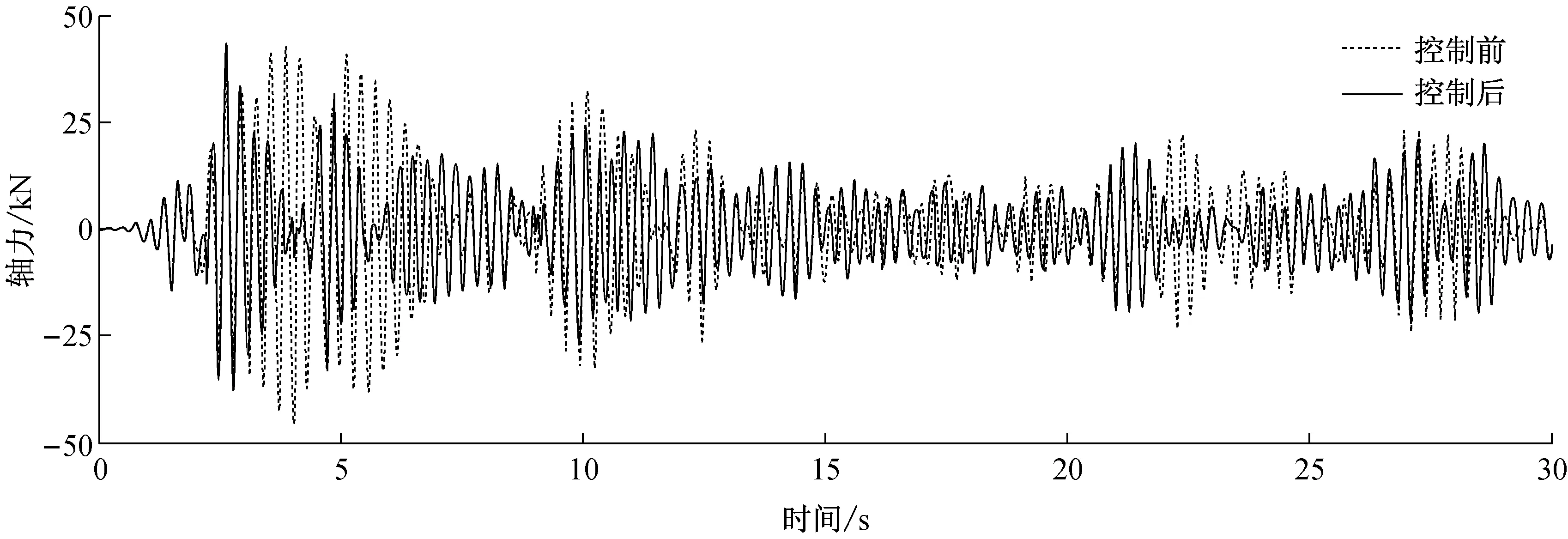
对减震控制前后的单层球面网壳结构采用时程法进行分析,选取El Centro(N-S)地震波,输入x向(水平)单向激励.El Centro地震波数据输入采用加速度原始记录,仅取前30 s,不修正,加速度峰值为0.342g,卓越周期为0.56 s.所选节点竖向位移响应和杆件轴力响应计算结果见表4.表中的最大值及均方根指对应各时间步动力响应的统计结果(下同).限于篇幅,本节仅列出杆件1在控制前后的轴力响应时程曲线,如图5a~5c所示.
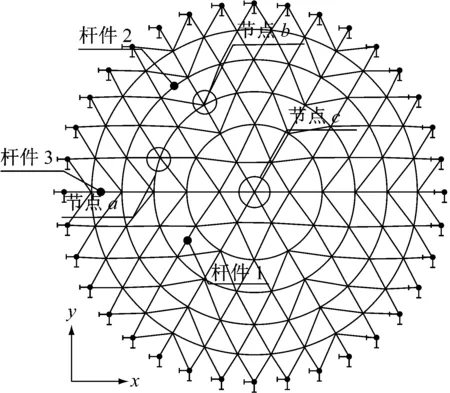
a 所关心杆件节点分布图
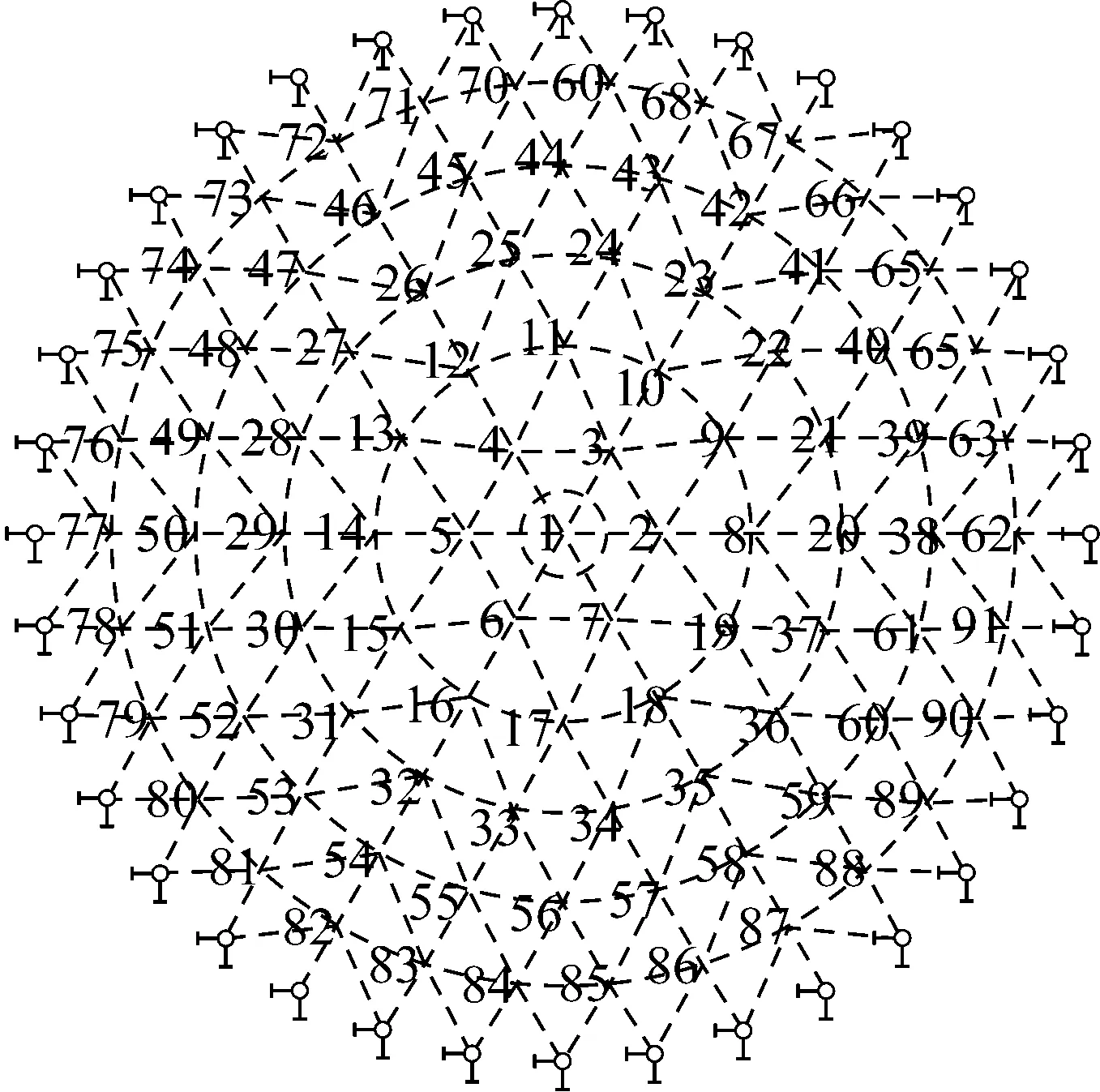
b 网壳节点编号图

控制方案控制振型详细布置方案方案一第2阶节点号13,1920,299,1528,3727,36f2=3.28Hz质量/kg18361835182718031798IMPF=42.1%刚度/(kN·m-1)782781778768766方案二第94阶节点号21,3039,5128,3749,6120,29f94=10.35Hz质量/kg18591842182218151762IMPF=24.9%刚度/(kN·m-1)78687795770876787455方案三第71阶节点号2,54,76,38,1410,12f71=4.89Hz质量/kg255625562556715715IMPF≈0刚度/(kN·m-1)241524152415678678

表4 不同减震方案下网壳时程反应计算结果比较(水平)
由表4中的计算结果可看出:(1)在水平地震作用下,各减震控制方案对减小网壳结构震动均有一定效果,总体来说,网壳减震效果方案一>方案二>方案三;(2)由于“减震控制方案一”所控制的振型(第2振型)参与系数最大,且最接近地震波卓越周期,所以减震效果最佳.从水平地震作用下位移较大的节点a来看,加速度响应减小47%左右;(3)由于三种控制方案设置的D-MTMD仅为竖向控制,径向杆(杆件1)减震效果较好,而环向杆(杆件2)减震效果相对较低.
3.3竖向地震减震控制分析
对竖向地震减震控制采用同样的分析方法,选取网壳结构z向主要参振模态(91阶,107阶)以及次要参振模态(第2阶),分别进行减震控制.由于竖向震动主要参与振型比较简单,且为使结构不产生偏心,各控制点关于结构对称布置,控制点取为7(6)个.各TMD质量和刚度的取法与水平地震分析相同.此外,本节增加方案四,对网壳所有节点(91个)进行控制,控制振型与方案一相同,即控制第91阶振型.各控制方案的D-MTMD配置见表5,不考虑各TMD的阻尼效应.
采用相同的时程分析方法,输入z向(竖直)El Centro(N-S)地震波,地震波参数同3.2.所选节点竖向位移响应和杆件轴力响应计算结果见表6;限于篇幅,仅列出节点c(顶点)在控制前后的竖向位移响应时程曲线,如图6a~6d所示.

a 方案一

b 方案二
c 方案三
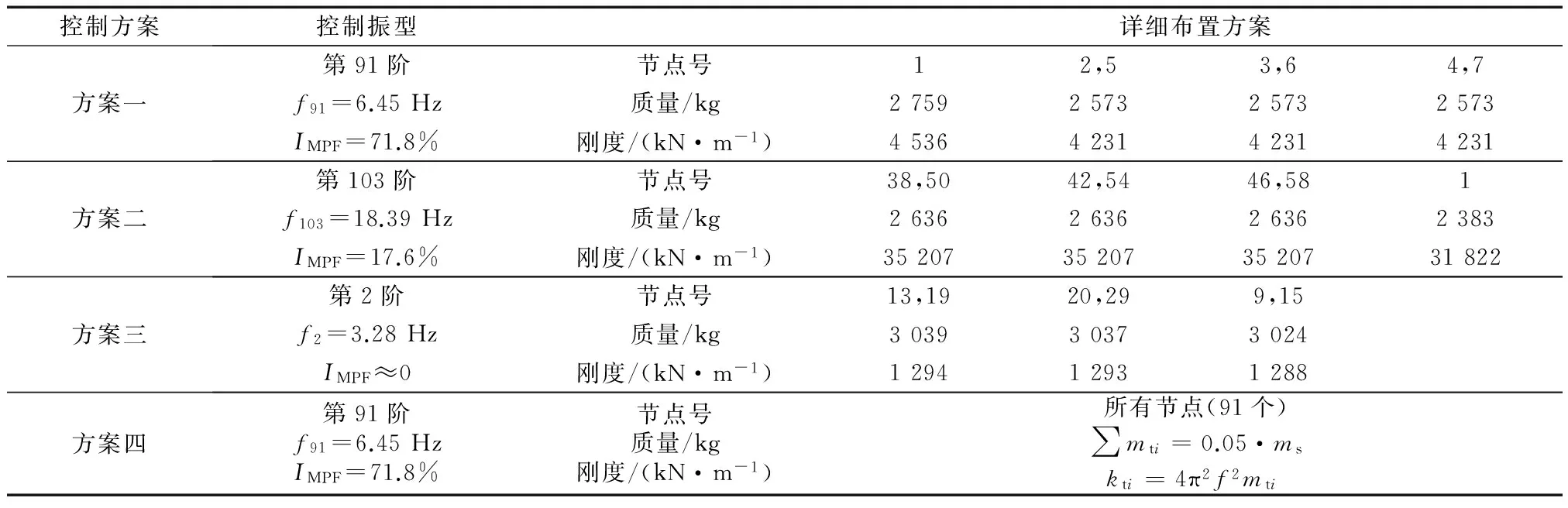
控制方案控制振型详细布置方案方案一第91阶节点号12,53,64,7f91=6.45Hz质量/kg2759257325732573IMPF=71.8%刚度/(kN·m-1)4536423142314231方案二第103阶节点号38,5042,5446,581f103=18.39Hz质量/kg2636263626362383IMPF=17.6%刚度/(kN·m-1)35207352073520731822方案三第2阶节点号13,1920,299,15f2=3.28Hz质量/kg303930373024IMPF≈0刚度/(kN·m-1)129412931288方案四第91阶f91=6.45HzIMPF=71.8%节点号质量/kg刚度/(kN·m-1)所有节点(91个)∑mti=0.05·mskti=4π2f2mti
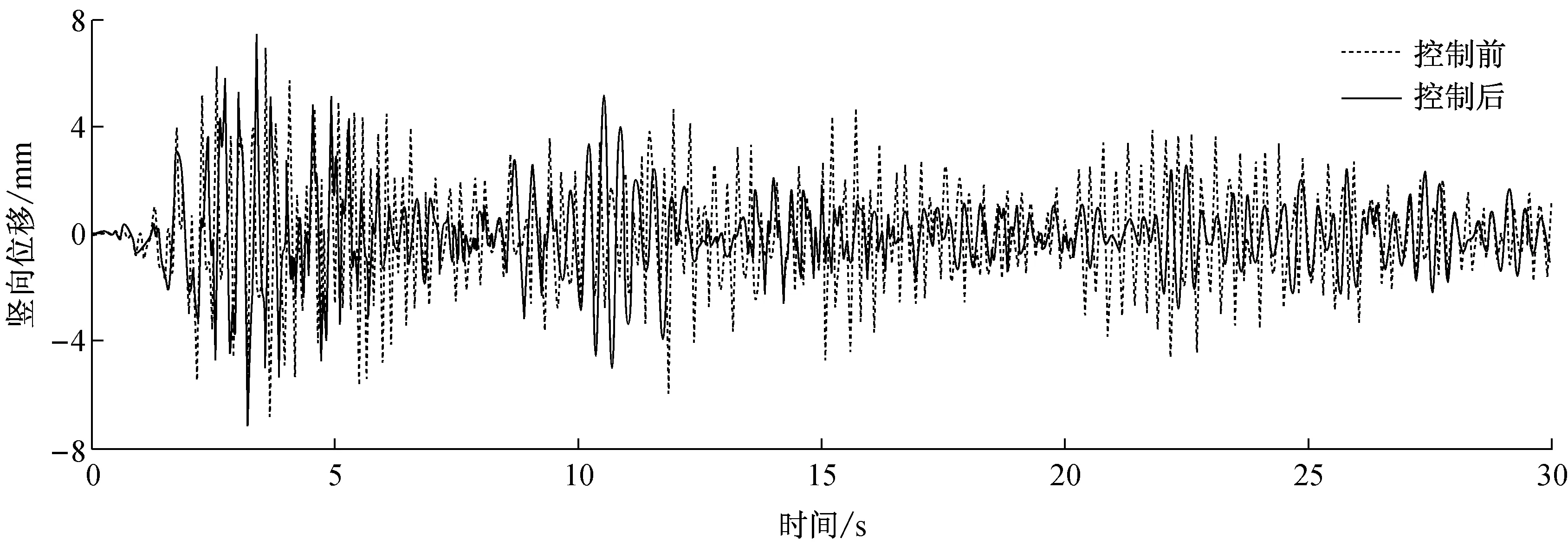
a 方案一
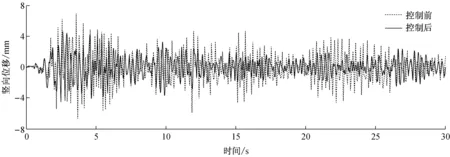
b 方案二
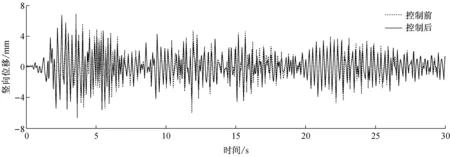
c 方案三
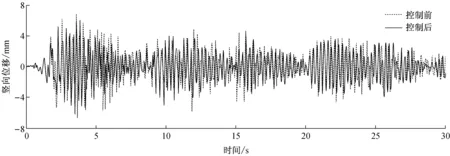
d 方案四

控制方案节点b竖向位移节点c竖向位移杆件2轴力杆件3轴力最大值/mm均方根/mm最大值/mm均方根/mm最大值/kN均方根/kN最大值/kN均方根/kN控制前4.61.16.91.953.512.544.38.0方案一4.41.27.41.563.614.737.58.1方案二4.51.24.71.346.311.535.27.7方案三3.91.06.81.747.510.542.28.1方案四4.10.96.11.744.88.841.17.5
3.4不同地震波控制效果对比
为了进一步验证本文提出的减震控制方法的普遍适用性,除第3.2节和3.3节中选取的El Centro波外,选取Taft波(Tg=0.34~0.38 s)和Mexico波(Tg=2~2.2 s)对模型分别进行水平和竖向地震反应的计算,并对减震效果进行分析对比,计算结果分别见表7—8.各方向控制方案均取质量参与系数最大的“方案一”.
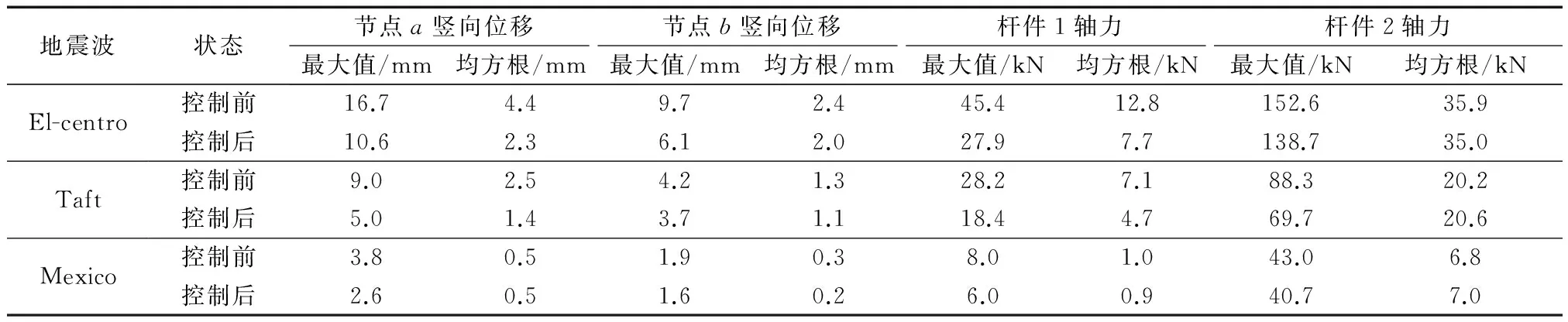
表7 不同水平地震波下网壳时程反应计算结果比较

表8 不同竖向地震波下网壳时程反应计算结果比较
由表7—8计算结果可知:(1)“水平控制方案一”对水平地震波的减震效果明显,但由于网壳控制频率远离Mexico波卓越频率,虽也有减震作用,但效果最小;(2)“竖向控制方案一”对竖向地震波的减震效果较差,对个别杆件动力响应甚至有所放大,具体原因见3.3节中的分析,一是控制频率与输入频率相差较远,二是所控频率简化控制方案所造成的偏差较大,需进一步研究.
4 结论
大跨度空间网壳结构的D-MTMD减震控制在国内外研究均处于起步阶段.本文通过理论推导,提出了基于固有模态的单层球面网壳结构D-MTMD减震控制方法,并对一网壳数值算例进行地震响应时程分析,得出以下主要结论:
(1)基于结构振型分解提出的基于固有模态的D-MTMD减震控制方法对网壳结构进行减震控制是可行且有效的;
(2)控制振型的选取是关键因素,不仅需要选取质量参与系数较大的振型,还应使其尽量接近地震波或场地的特征周期;
(3)对空间网壳结构进行D-MTMD震动控制,并不是对所有构件都有较好的控制效果,个别杆件的动力响应反而会增大,所以,应该合理制定D-MTMD减震控制方案,保证一些重要的杆件有较好的减震控制效果.
本文提出的基于固有模态的单层球面网壳结构D-MTMD减震控制方法,在空间结构减震控制设计领域,具有良好的前景.本文仅定性地在弹性范围内验证了该减震控制方法控制单一振型的有效性,在减震控制的空间结构形式、多振型控制组合、控制装置的参数优化等方面均还有大量的课题有待研究.
[1]廖冰, 罗永峰. 基于振型贡献系数的空间结构振动反应研究[J]. 空间结构, 2014,20(1):9.
LIAO Bin, LUO Yongfeng. Vibration response computation of spatial structures based on mode contribution factors[J]. Spatial Structures, 2014,20(1):9.
[2]廖冰, 罗永峰, 王磊, 等. 基于质量参与系数的空间结构动力模型简化[J]. 湖南大学学报: 自然科学版, 2013,40(9):7.
LIAO Bin, LUO Yongfeng, WANG Lei,etal. A new simplified method for the dynamic model of spatial structures[J]. Journal of Hunan University:Natural Sciences, 2013,40(9):7.
[3]LUO Yongfeng, WANG Lei, GUO Xiaonong. Threshold value method and its application in dynamic analysis of spatial latticed structures[J]. Advances in Structural Engineering, 2012,15(12):2215.
[4]叶继红, 陈月明, 沈世钊. TMD减震系统在网壳结构中的应用[J]. 哈尔滨建筑大学学报, 2000,33(5):10.
YE Jihong,CHEN Yueming,SHEN Shizhao. The present situation of seismic vibration control of reticulated shell structures using TMD system [J]. Journal of Harbin University of Civil Engineering and Architecture,2000,33(5):10.
[5]叶继红, 陈月明, 沈世钊. 网壳结构TMD减震系统的优化设计[J]. 振动工程学报, 2000,13(3):376.
YE Jihong,CHEN Yueming,SHEN Shizhao. Optimum design for reticulated shell structure-TMD systems subjected to seismic excitations [J]. Journal of Vibration Engineering, 2000,13(3):376.
[6]胡继军, 黄金枝, 李春祥, 等. 网壳-TMD风振控制分析[J]. 建筑结构学报, 2001,22(3):31.
HU Jijun,HUANG Jinzhi,LI Chunxiang,etal. TMD control analysis of reticulated shells for wind vibration[J]. Journal of Building Structures,2001,22(3):31.
[7]林勇建, 周晅毅, 顾明. 柱面网壳结构MTMD风振控制研究[J]. 结构工程师, 2013,29(2):114.
LIN Yongjian,ZHOU Xuanyi,GU Ming. MTMD control analysis of a cylindrical lattice roof structure for wind- induced vibration[J]. Structural Engineers,2013,29(2):114.
[8]唐柏鉴, 王治均. 大跨网格屋盖结构竖向MTMD减震控制的参数分析[J]. 工程力学, 2009,26(5):130.
TANG Baijian,WANG Zhijun. Parametric analysis of vertical MTMD in long-span lattice roof structures[J]. Engineering Mechanics,2009,26(5):130.
[9]Yamada M. Vibration control of large space structure using TMD system[C]// 15th Asian-Pacific Conference on Structural Engineering and Construction. Queensland: ASEC, 1995:23-30.
[10]Yoshinaka S, Kawaguchi K. Vibration control of spatial structures using spatially distributed MTMDs[J]. Memoirs of the Faculty of Engineering Osaka City University, 2008,49:19.
[11]Tsuda S, Ohsaki M. Bi-directional seismic vibration control of spatial structures using passive mass damper consisting of compliant mechanism[C/CD]// Proceeding of International IASS Conference. Seoul: IASS, 2012.
[12]Yamakawa M, Yoshinaka S, Araki Y,etal. Estimation of the global optimality for multiple tuned mass damper systems using order statistics [C/CD]// Proceeding of 11th. World Congress on Computational Mechanics,Barcelona: WCCM XI, 2014.
[13]李春祥, 黄金枝. 高层钢结构MTMD地震反应控制优化设计[J]. 振动与冲击, 2000,19(1):37.
LI Chunxiang, HUANG Jinzhi. The optimum design of MTMD control for earthquake excited steel tall building[J]. Journal of Vibration and Shock, 2000,19(1):37.
[14]Fu T S, Johnson E A. Distributed mass damper system for integrating structural and environmental controls in buildings[J]. Journal of Engineering Mechanics, 2010,137(3):205.
[15]胡仲淹, 罗永峰, 王人鹏, 等. 基于振型遴选与振型构造的空间网格结构动力分析方法[J]. 工业建筑, 2015,45(1):16.
HU Zhongyan, LUO Yongfeng, WANG Renpeng,etal. The dynamic analysis of spatial lattice structures based on mode selection and mode construction techniques[J], Industrial Construction, 2015,45(1):16.
Seismic Vibration Control Analysis of Single Layer Spherical Reticulated Shell Based on the Natural Modes
LIU Yipeng,LUO Yongfeng,XIANG Yang
(College of Civil Engineering,Tongji university, Shanghai 200092, China)
The developments and research status of seismic vibration control of long-span spatial structures using multiple tuned mass damper (MTMD) are introduced in this paper. The dynamic equation of reticulated shell with MTMD vibration control system is derived and solved. Based on controlling selected natural modes, the design procedure of distributed multiple tuned mass damper (D-MTMD) seismic control method of the single layer spherical reticulated shell is proposed. A numerical model of single layer reticulated shell is built. By the method of time-history analysis with “El Centro seismic waves”, the dynamic responses of the reticulated shell structure equipped with different seismic vibration control schemes are computed, analysed and compared under horizontal and vertical seismic excitations. The numerical results show that the proposed seismic vibration control method is efficient in reducing dynamic response of reticulated shell structures. Beyond that, some suggestions for seismic vibration control optimization design are summarized.
natural mode; single layer spherical reticulated shell; distributed multiple tuned mass dampers; seismic vibration control
2015-03-11
国家自然科学基金(51378379)
刘怡鹏(1989—),男,博士生,主要研究方向为钢结构.E-mail:liuyp12@126.com
罗永峰(1957—),男,工学博士,教授,博士生导师,主要研究方向为钢结构.E-mail:yfluo93@tongji.edu.cn
TU393.3
A
