寒区隧道保温层铺设长度的计算方法
2016-10-18夏才初范东方
夏才初, 范东方,2, 李 强, 何 佳,3
(1.同济大学 土木工程学院,上海 200092;2.中铁第四勘察设计院集团有限公司,武汉 430063;3.四川省交通运输厅公路规划勘察设计研究院,成都 610041)
寒区隧道保温层铺设长度的计算方法
夏才初1, 范东方1,2, 李强1, 何佳1,3
(1.同济大学 土木工程学院,上海 200092;2.中铁第四勘察设计院集团有限公司,武汉 430063;3.四川省交通运输厅公路规划勘察设计研究院,成都 610041)
目前寒区隧道保温层铺设长度的设计要求隧道洞内温度场已知,为克服设计时暂无洞内气温实测资料的问题,基于由隧道进、出口气象条件及隧道地形条件求解的温度场解析解,提出了一种保温层铺设长度的计算方法.首先根据由隧道进口气象参数得到的洞内空气年温度振幅与由出口气象参数得到的洞内空气年温度振幅相等这一条件,计算得到受进出口气象影响的临界长度lM.当距隧道进口的长度小于临界长度lM时,利用进口气象参数计算隧道进口段围岩及衬砌温度场;当距隧道进口的长度大于临界长度lM时,利用出口气象参数计算出口段围岩及衬砌温度场,然后由隧道温度场中初期支护与围岩交界面出现0 ℃的位置确定保温层铺设长度.在铺设保温层后,洞内空气与围岩的对流换热发生变化,根据未铺设保温层和铺设保温层两种情况下的流入控制体的能量相等的条件,推导了保温层铺设长度的修正系数,从而计算出保温层铺设的最终长度.结合实际工程,利用提出的方法计算出保温层铺设长度,分析了关键参数对铺设长度的影响,结果表明:铺设长度随着地温梯度的增加逐渐减小,铺设长度随洞内风速的增加迅速增大.
寒区隧道; 保温层长度; 温度场; 地温梯度; 洞内风速
在进行寒区隧道抗防冻设计时,保温层铺设长度的合理取值十分重要,过短则起不到防止围岩冻融的作用,过长又会增加不必要的工程投资.从工程实践看,国内新建的寒区隧道多是通过工程类比法来确定保温层的铺设长度,但由于不同的寒区隧道气象、地形条件差异很大,导致不同隧道温度场区别很大,类比结果与实际情况也可能会有较大的差异.
国内多条寒区隧道进行了温度场的现场监测及研究[1-6],并获得了寒区隧道径向、轴向温度场变化规律,但这种现场监测需要投入大量的人力和物力,研究成本非常高;同时现场监测存在滞后性,即隧道设计、施工完成后才能获得隧道洞内温度场分布规律.
赖远明[7]、张耀[8]等开展了隧道温度场的理论计算研究,但得出的计算方法均要求隧道洞内气温已知,当洞内气温未知时,则无法进行围岩温度场的求解.国外学者Krarti[9]、Takumi[10]利用叠加原理和能量守恒原理求得了寒区隧道空气温度场的解析解,但该解析解并不适用于考虑保温层、二次衬砌、初期支护和围岩等多层介质的寒区隧道温度场的求解.夏才初提出了一种根据隧道进、出口气象条件及隧道地形条件求解洞内空气及围岩温度场的解析方法[11],克服了现有解析解对隧道洞内空气温度场监测的依赖,使保温层铺设长度计算结果更准确.本文即基于该隧道衬砌和围岩温度场理论解,提出了保温层铺设长度的计算方法,为寒区隧道防抗冻设计提供了理论依据.
1 寒区隧道洞内空气及围岩温度场解析解[11]简介
隧道运行后,洞内空气温度在一年之中会呈三角函数的形式变化,受洞内空气温度场的影响,沿隧道径向一定范围内的围岩温度也会随时间变化.假设空气不可压缩,在隧道内外压差作用下,隧道洞内风向以轴向为主,根据质量守恒定律,在隧道断面不变的条件下,风速为恒定值.另外在同一横断面,不同位置处的空气温度值存在差异,但温差很小,可假定同一横断面内的气温值相等.
为得到隧道衬砌和围岩温度场解析解,做如下几点简化和假设:(1)隧道断面为圆形.(2)不考虑衬砌与围岩之间的接触热阻.(3)洞内气温只沿隧道轴线方向变化.(4)洞内空气的流速为恒定值.
此时隧道径向传热模型如图1所示,隧道洞内气温轴向传热模型如图2所示.图1中,r、θ代表极坐标,r0为保温层内半径,r1为二衬内半径,r2和r3分别为初衬内、外半径,rd为隧道围岩温度场影响深度,To为恒温层围岩的温度,f(z,t)为洞内气温.图2中,To(t)为洞口温度,T1(r0,t)为洞壁处的温度,qz为围岩与洞内空气传递的热量,Vf为洞内空气风速,dz为隧道洞内空气微元体.
夏才初根据圆形多层介质热传导理论及空气能量守恒定理获得了距离洞口任意距离z处、距洞壁任意深度r处和任意时刻t时的隧道内空气、保温层、衬砌和围岩的温度场[11].
(1)
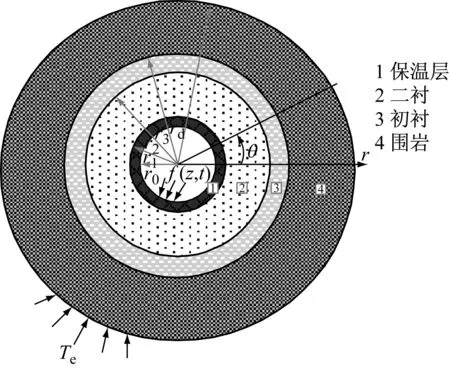
图1 隧道径向热传导计算模型
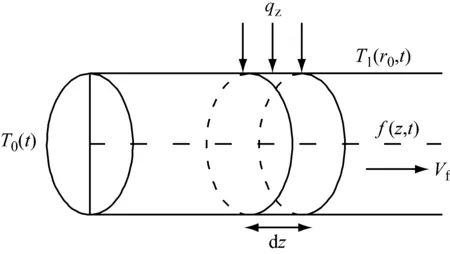
图2 隧道洞内气温轴向传热模型
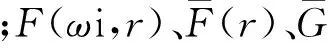
2 保温层铺设长度的计算方法
2.1保温层铺设长度的初步计算
保温层铺设长度的计算步骤是:
(1)确定进、出口年平均气温、年温度振幅、隧道埋深函数(隧道埋深随里程的变化)、材料热物理参数等各项已知条件;由于除进出洞口一小段外,隧道埋深都大于外部环境对地层温度的影响深度,因此,
外部环境对整个隧道衬砌和围岩温度场的影响基本可以忽略.
(2)无论是进口气温还是出口气温,对隧道内空气温度的影响都是通风流动与由温差引起的传热两个方面.当风速为0的极端情况,进口段和出口段对隧道内空气温度的影响只受进口段和出口段与隧道内空气温度差的影响,当风速较大时,通风流动对隧道内空气温度起主导作用,此时进口气温对其影响较大;当风速足够大时,出口气温对隧道洞内空气温度的影响基本可以忽略不计.而在自然通风情况下,风速较小,沿隧道纵向的温度场分布既受进口气象的影响,又受出口气象的影响,因此,在求解温度场之前,首先要划分出进口段(受进口气象的影响)和出口段(受出口气象的影响),划分方法为:设在距离隧道进口lM处,由进口处气象参数确定的洞内空气年温度振幅与出口处气象参数确定的洞内空气年温度振幅相等.即:
(2)
式中:Tin,A为进口处空气年温度振幅;Tout,A为出口处空气年温度振幅;Vf为洞内空气风速;l0为隧道总长度.TA1为由进口气象参数确定的洞内年温度振幅;TA2为由出口气象参数确定的洞内年温度振幅,TA1和TA2计算式分别为
式中:ρ为空气密度;cp为隧道内空气比热容;h为围岩与洞内空气的对流换热系数,z为距洞口距离,i为虚数单位.
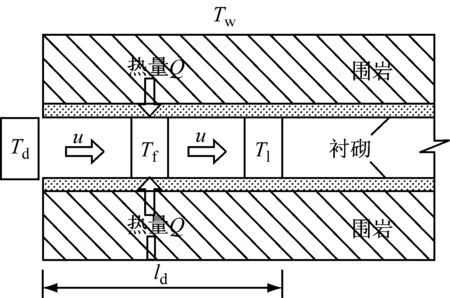
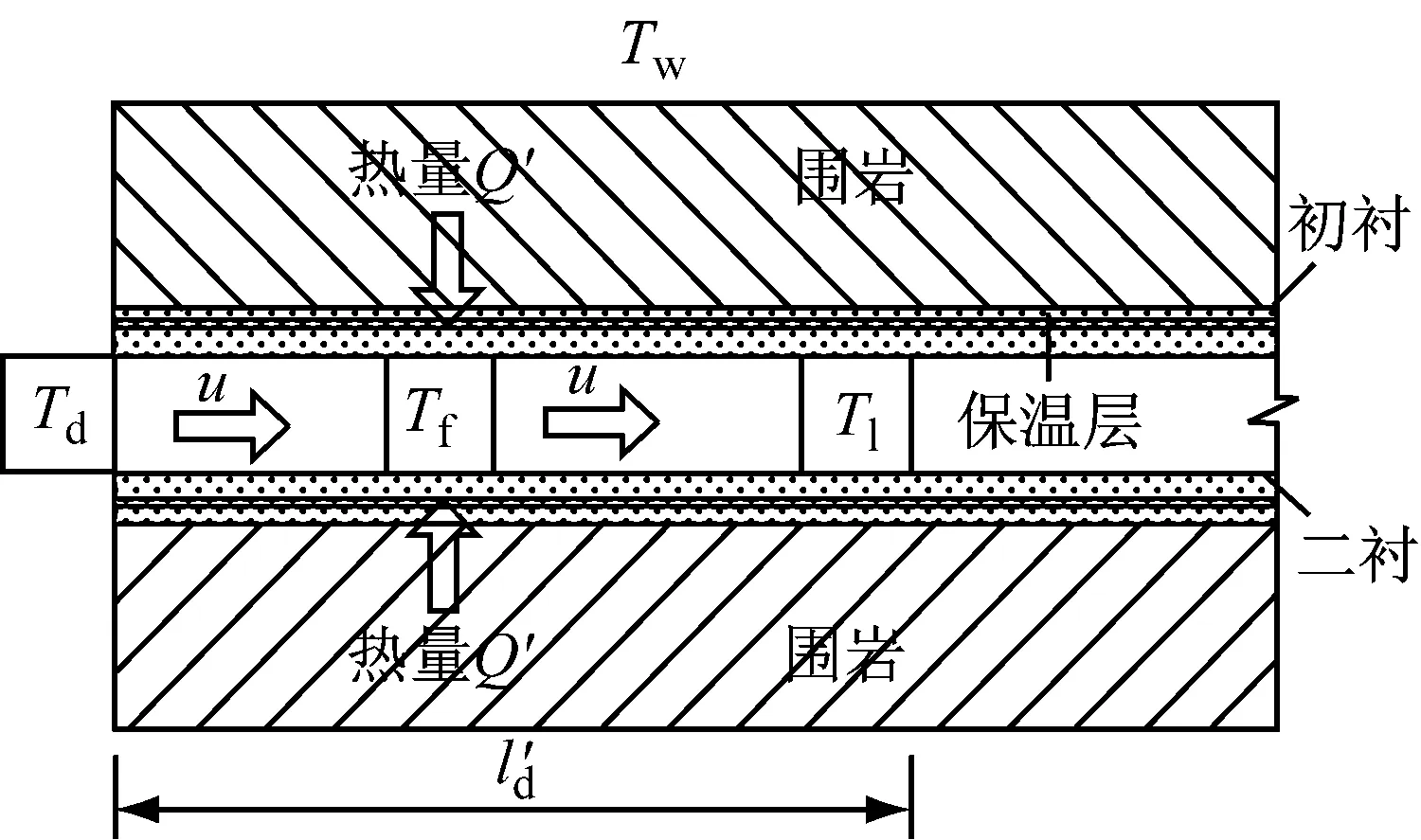
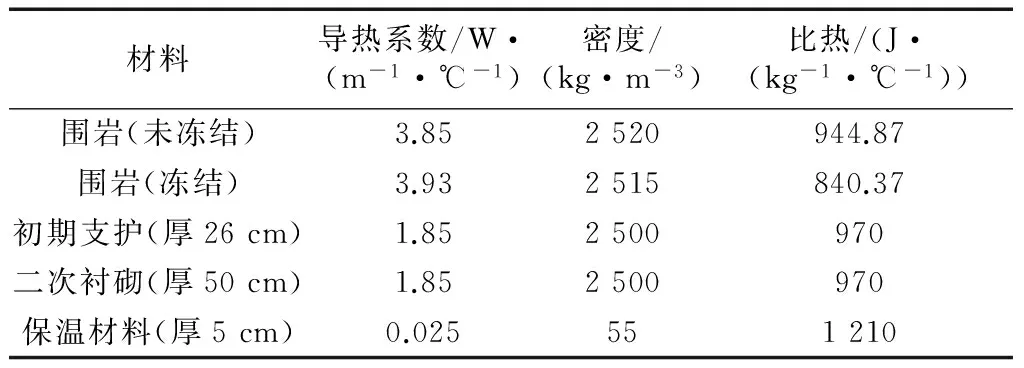
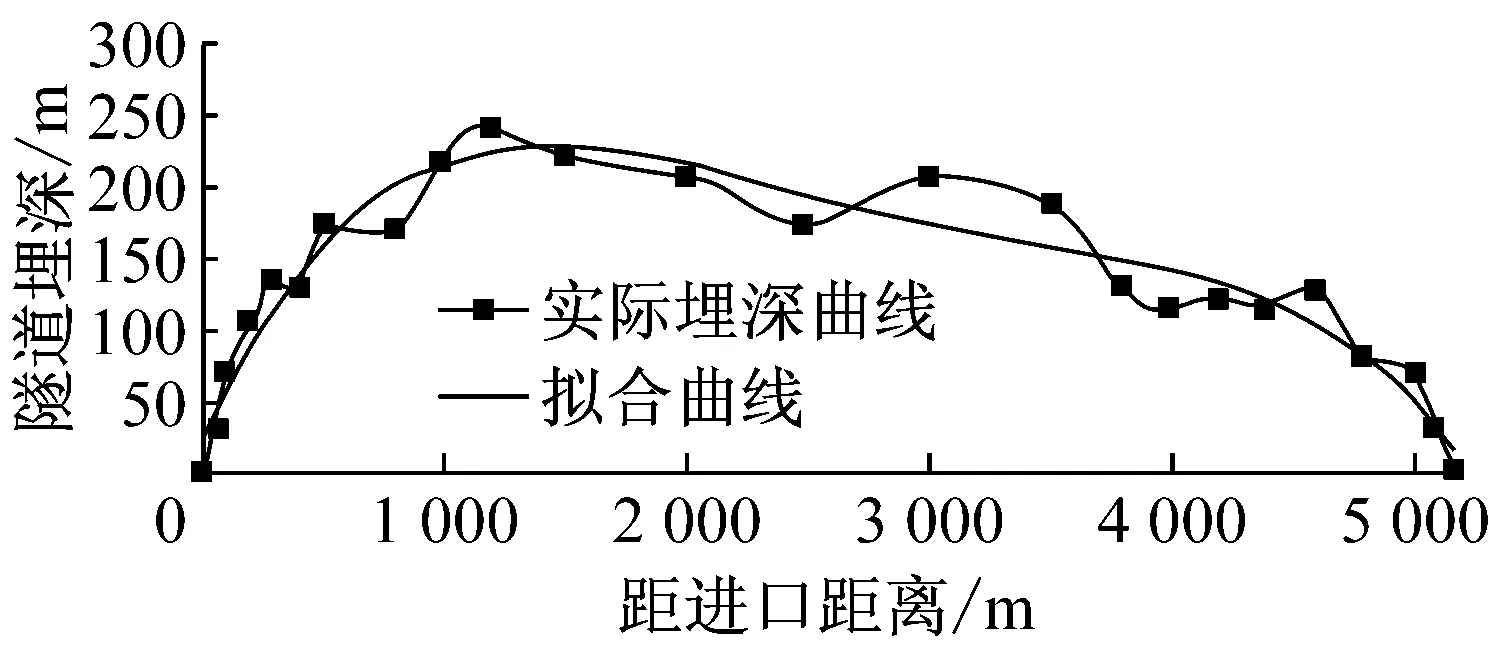
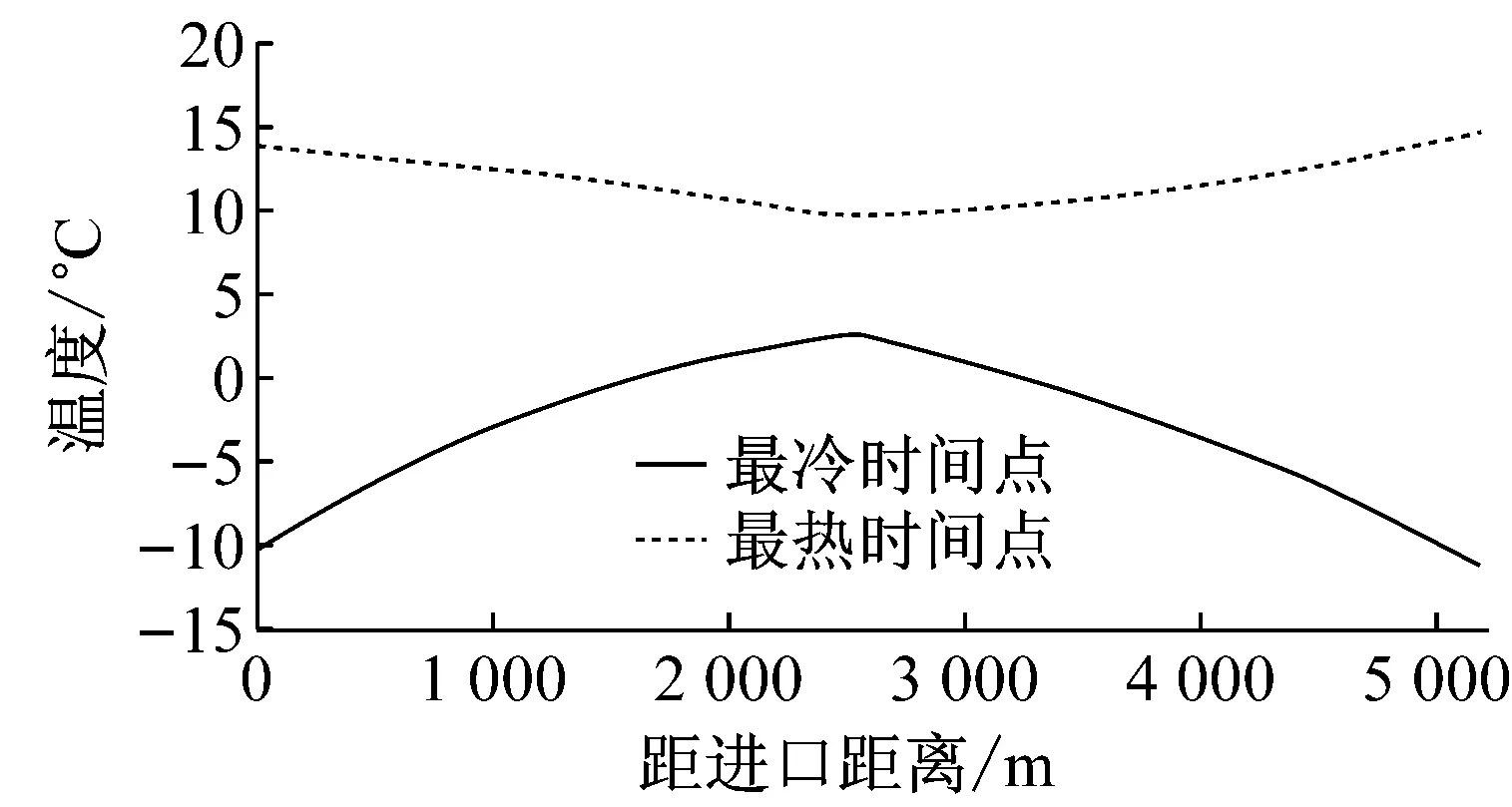
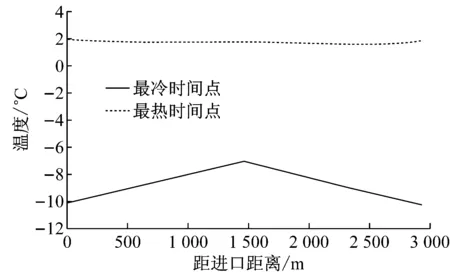
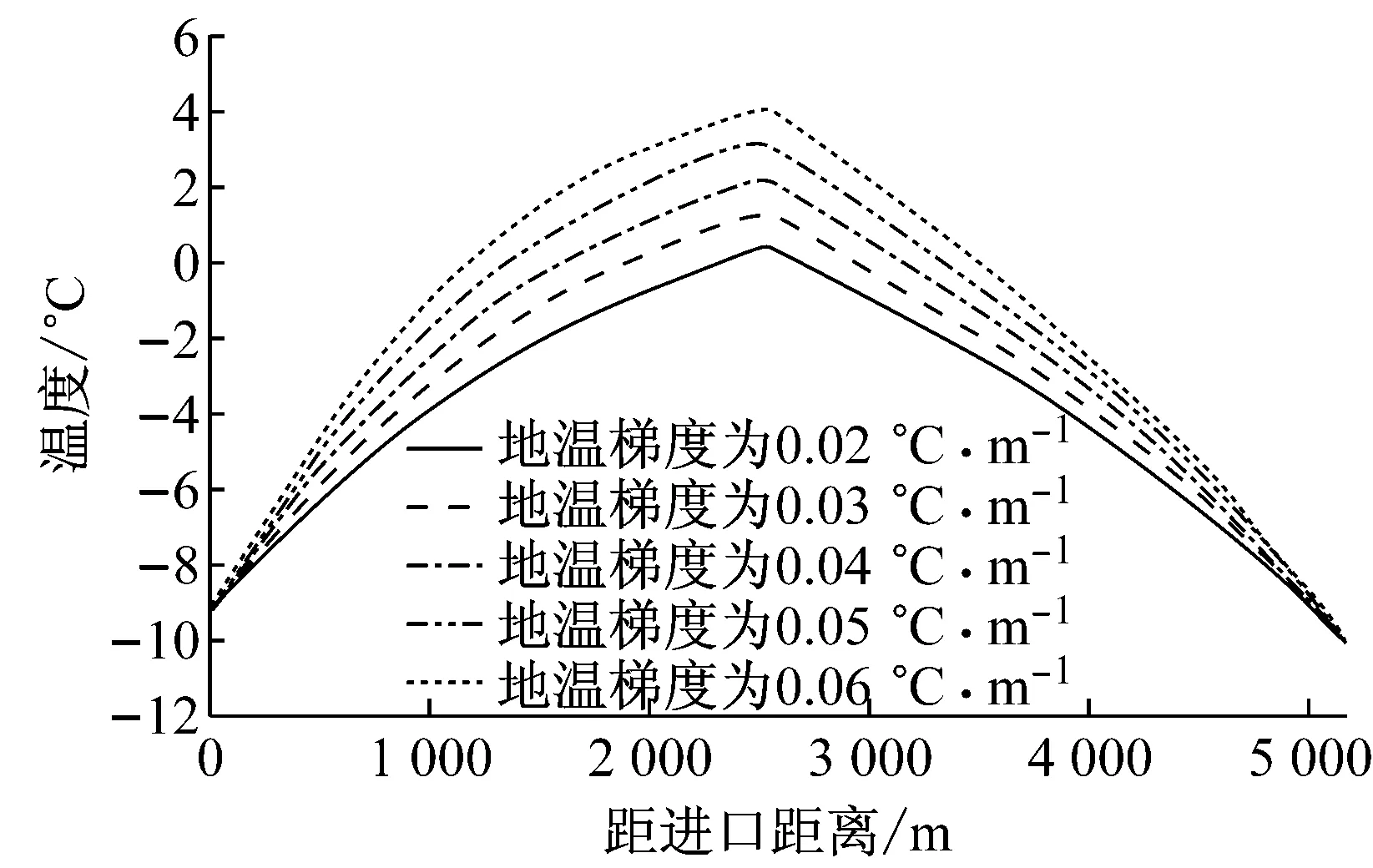
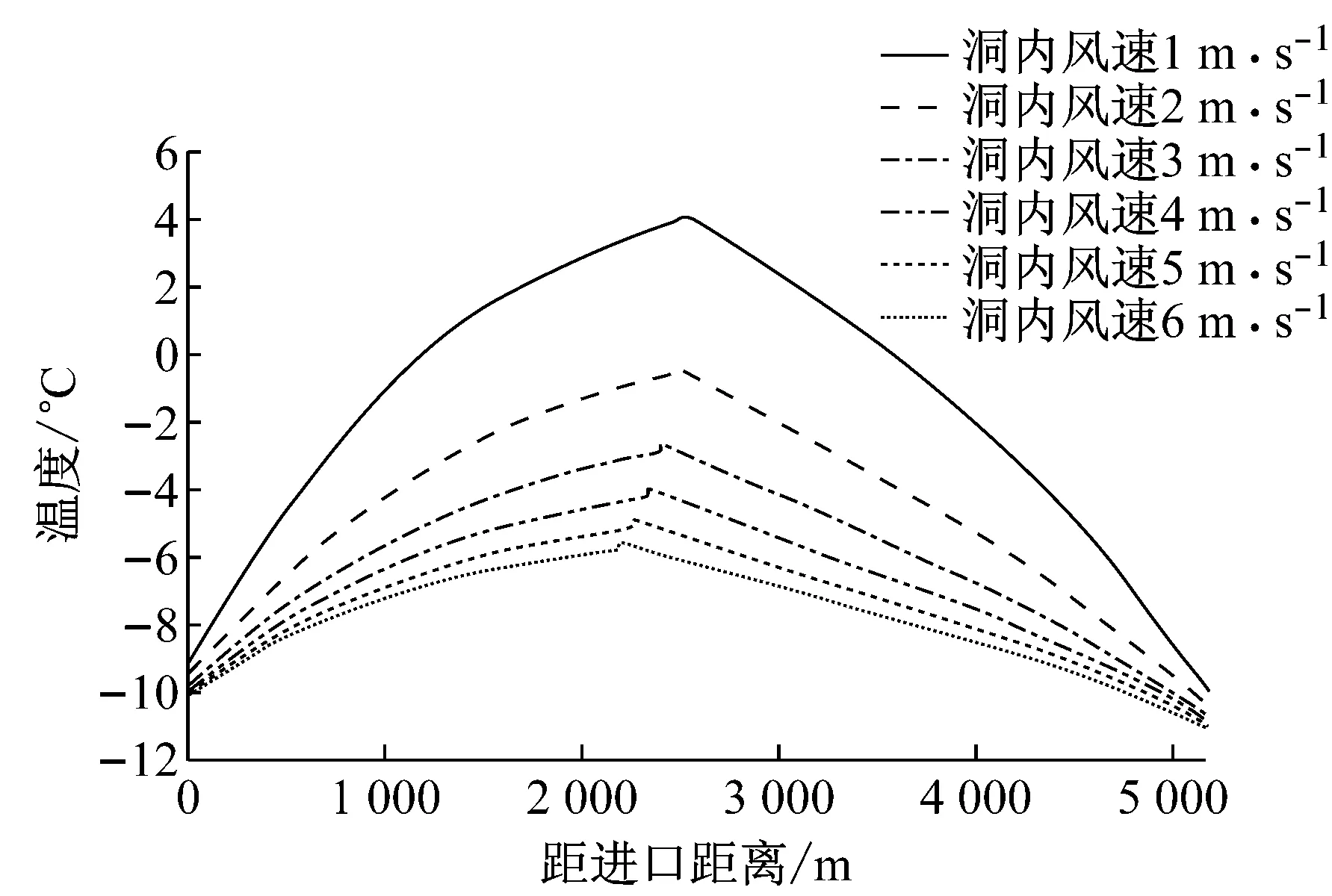
将已知参数代入式(1)即可求得lM,当0≤l≤lM时,利用进口气象参数计算隧道进口段围岩及衬砌温度场;当lM 将各已知参数代入围岩温度场解析解式(1),即可分别求出无保温层时隧道进口段沿长度方向的围岩及衬砌温度分布,以及出口段沿长度方向的围岩及衬砌温度分布,合并在一起即构成了沿隧道整个长度方向的围岩及衬砌温度分布. (3)对于多年冻土,当在距隧道进口或出口某一长度lb处,初期支护与围岩交界面温度已小于或等于0 ℃,则取lb为保温层的铺设长度;对于非冻土,当在距隧道进口或出口某一长度lb处,二次衬砌内表面的温度已大于0 ℃(双层铺设、离壁铺设、表面铺设时)或者初期支护与二次衬砌交界面的温度已大于0 ℃(夹层铺设时),则取lb为保温层的铺设长度.计算过程可用图3所示的流程图表示(以多年冻土为例). 图3 保温层铺设长度计算流程 2.2保温层铺设长度的修正 第2.1节得到的保温层铺设长度是基于保温层未铺设的情况进行求解的,当铺设了保温层后,洞内空气与围岩的对流换热情况又发生了变化. (1)不铺设保温层 此时隧道内空气与非冻土围岩的换热过程如图4所示. 选取隧道洞口单位长度内的空气为控制体,在洞外的初始温度为Td,以速度u向隧道内运动,到达第2.1节初步计算的需设防位置(x=lb)时,温度升高为Tl.在一定时间内,进入控制体的能量Ei为空气与隧道内壁进行对流换热得到的能量.从洞口(温度为Td)的位置到距进口lb处(温度为Tl)的位置需要的时间τ=lb/u,计空气与围岩之间的热流量为Q,则 (3) 该问题属于带有对流边界条件的一维多层圆筒壁热传导问题[12].因此 (4) 式中:Tw为一定深度处围岩的恒定温度;Tf为空气的平均温度,Tf=(Td+Tl)/2;h1为空气与隧道内壁间的平均对流换热系数;A1为对流换热面积,A1 =2πr5lb;r5为隧道的当量半径;r6为衬砌外侧(靠近围岩侧)的半径(无保温层);r7为围岩温度恒定处的半径(无保温层);λ2为衬砌的导热系数;λ3为围岩的导热系数. 图4 空气与非冻土围岩换热模型(无保温层) Fig.4Heat exchange between air and non-frozen rock without insulation layer (2)铺设保温层 (5) 设铺设保温层后空气与围岩之间的热流量为Q′,则有: (6) (7) (8) 同理可以推出保温层表面铺设和离壁铺设的长度修正系数. 图5 空气与非冻土围岩换热模型(有保温层) Fig.5Heat exchange between air and non-frozen rock with insulation layer 3.1季节冻土区实例 3.1.1工程概况 白茫雪山1#隧道长5 180 m,最大埋深243.65 m,进出口设计高程4 113.15~4 069.99 m,隧址区自然气候条件较为特殊,“立体气候”明显,属于寒温带山地季风气候,气温随海拔高度增加而降低,年内最高气温在金沙江及河谷地区,每年6月可达30 ℃以上,最低气温在一般高山区,每年1~2月份可达-16 ℃. 3.1.2保温层长度计算 根据设计资料,隧道当量半径取为3.97 m,外边界取13 m,洞外气象监测数据显示,隧道进、出口年平均气温相同,均为1.38 ℃,年振幅进、出口分别为19.05 ℃和20.5 ℃.自然通风情况下的年平均风速为1.32 m·s-1,空气与洞壁的对流换热系数取:h=6.2+4.2·Vf[13],空气对地表以下土壤温度场的影响深度为20 m[14],空气密度ρ取为0.74 kg·m-3,空气比热容cp取为0.95 J·(kg-1·℃-1).衬砌、围岩及保温材料的参数见表1. 表1 材料参数 根据现场实测数据拟合得到隧道围岩初始温度T0=Tm+2+K·(H-20),其中Tm为年平均温度,K为地温梯度,实测为0.04 ℃·m-1,H为隧道埋深. 保温层铺设长度计算过程如下: (1)首先将进、出口气象参数分别代入式(2)求出lM: TA1(19.05,1.32,lM)-TA2(20.50, 1.32,5 180-lM)=0, 解得lM=2 524.77m (2)白茫雪山1#隧道埋深与距进口的距离关系如图6所示,将隧道埋深数据进行拟合(每隔100 m取一个埋深值)可以得到隧道埋深H随洞口水平距离l变化的数学表达式: H(l)=21.880 41+0.375 96l- 2.316 83×10-4·l2+ 5.546 41×10-8·l3- 4.788 22×10-12·l4 (3)将各参数代入寒区隧道洞内空气及围岩温度场解析解式(8),求得沿隧道长度方向衬砌的温度分布.计算结果如图7所示. 图6 隧道埋深随距进口距离的变化曲线 图7 不铺设保温层时初期支护与二次衬砌交界面温度分布 Fig.7Temperature on the interface of primary lining and secondary lining without insulation layer 可以看出,暖季洞内温度“中间低,两端高”;寒季洞内温度“中间高,两端低”.这是由于在暖季,外界空气温度高于围岩温度,空气在穿过隧道过程中不断散热,越往中间温度越低,因此越靠近隧道洞口,空气与衬砌的温差越大,衬砌吸收的热量越多,衬砌温度上升得越多,所以初期支护与二次衬砌交界面的温度出现两端高,中间低的现象,而寒季则相反.不铺保温层时,在一年之中最冷时间点,距进口1 594 m、距出口1 969 m处初期支护与二次衬砌交界面温度达到0 ℃,这两点之间的隧道初期支护与二次衬砌交界面温度已经为正温,也就是说即使不铺设保温层,隧道初期支护、二次衬砌之间的防排水系统及其背后围岩也不会受冻.因此,白茫雪山1#隧道保温层铺设长度初步取为:进口段长1 594 m、出口段长1 969 m. 铺设了保温层后,洞内空气与围岩的对流换热受到阻碍,需对保温层铺设长度进行修正,采用式(8)求得修正系数m=1.33,因此,白茫雪山1#隧道保温层合理铺设长度为:进口段长2 121 m、出口段长2 619 m. 3.2多年冻土区实例 3.2.1工程概况 姜路岭隧道为双洞分离式隧道,位于青海省海南州,海拔高度4 280 m,左线长2 925 m,右线长2 845 m;隧址区为典型的高原大陆性半干旱气候类型,全年冰冻期长达7个月,年平均气温-4.2 ℃,年平均最高气温3.5 ℃,年最低气温-10.3 ℃. 3.2.2保温层长度计算 根据设计资料,隧道当量半径取为4.36 m,外边界取13 m,洞外气象监测数据显示,隧道进、出口年平均气温相同,均为-4.2 ℃,隧道进、出口空气年温度振幅为13.8 ℃.自然通风情况下的年平均风速为2 m·s-1,空气与洞壁的对流换热系数和空气对地表以下土壤温度场的影响深度的取值同3.1.1节,空气密度ρ取为0.82 kg·m-3,空气比热容cp取为1.07 J·kg-1·℃-1.衬砌、围岩及保温材料的参数见表2. 表2 材料参数 根据现场实测数据拟合得到隧道围岩初始温度T0=Tm+4.2+K·(H-40),其中K为地温梯度,实测为0.04 ℃·m-1. 将隧道埋深数据进行拟合可以得到隧道埋深H随距洞口水平距离l变化的数学表达式: H(l)=4.343 51+0.179 37l+ 7.448 36×10-5·l2- 9.786 6×10-8·l3+ 1.641 53×10-11·l4 利用第2节中的计算方法,求得沿隧道长度方向衬砌及围岩的温度分布.计算结果如图8所示: 图8不铺设保温层时初期支护与二次衬砌交界面温度分布图 Fig.8Temperature on the interface of primary lining and secondary lining without insulation layer 可以看出,在一年最冷时间点时,隧道全长衬砌及围岩温度均为负温,即不铺设保温层时,隧道非冻土段会遭受冻害;在一年最热时间点时,隧道全长温度变化较小,这是由于在最热时间点外部环境空气的温度(3.5 ℃)低于隧道中部非冻土段的原始温度(4.9 ℃),在进口段,洞内空气温度高于围岩温度,空气放热,衬砌吸热,温度升高,当空气进入隧道一段距离(910 m)之后,围岩温度反而稍高于空气温度,空气吸热,此时衬砌放热,温度降低,导致隧道全长温度相近.该时刻隧道多年冻土段的温度高于0 ℃,需要铺设保温层防止冻土融化.因此,需在隧道全长铺设保温层才能保证隧道多年冻土段不融化,非冻土段不冻结. 3.3与现有计算方法的比较 现有保温层铺设长度计算方法为日本学者黑川羲范提出的基于实测数据回归分析处理后的经验公式[15]: (9) 式中:x为洞口空气计算温度,其值取为最冷月平均温度减10 ℃. 对于白茫雪山1#隧道由该经验公式计算得到的保温层铺设长度为进口段1 136 m、出口段1 177 m,小于本文计算方法得到的进口段2 121 m、出口段2 619 m. 而该隧道设计时,出于经济性考虑,通过经验类比法初选方案为进口段、出口段各铺设保温层1 000 m,该长度小于经验公式和本文方法计算所得结果,因此隧道承受较大冻害风险,目前隧道尚未贯通,待其贯通后,运营单位将密切关注、监测其状况,一旦出现冻害,再进一步采取防、抗冻措施. 相对于经验类比方法和现有经验公式计算方法,本文保温层长度计算方法基于隧道衬砌和围岩温度场理论解提出,具有空气、隧道及围岩传热的热力学理论基础,而且该方法考虑了主要因素的影响,包括:隧址区地理地质条件、隧道衬砌厚度及热物理性质、隧道初始温度场及隧道沿纵向的埋深、洞内空气风速,更能够体现各因素对保温层长度设计的影响规律,能针对不同隧道在不同工况下计算出相应的保温层铺设长度. 以白茫雪山1#隧道为计算模型,对其中的地温梯度和隧道风速进行参数分析. 4.1地温梯度对保温层铺设长度的影响 洞内空气与衬砌、围岩发生热传导,因此隧道纵向温度场与围岩的初始温度有密切的关系,围岩初始温度T0=Tm+2+K·(H-20)由Tm,K,H决定,其中Tm,H由实测得到,根据文献[16]和白茫雪山1#隧道实测数据地温梯度分别取为0.02、0.03、0.04、0.05、0.06计算隧道在最冷时间点的温度场,其结果如图9所示. 由图9可知:随着地温梯度的增加,隧道初期支护与二次衬砌交界面最低温度逐渐升高,因此隧道所需的保温层铺设长度逐渐减小,减小幅度可达50%. 图9 初期支护和二次衬砌交界面温度与地温梯度的关系 Fig.9Temperature on the interface of primary lining and secondary lining versus geothermal gradient 4.2风速对保温层铺设长度的影响 洞内空气与隧道二次衬砌发生对流换热,对流换热系数与洞内空气的风速有关,因此隧道纵向温度场受洞内空气风速的影响,取风速为1,2,3,4,5,6 m·s-1(该隧道通风设计风速为5.6 m·s-1)进行计算.隧道在最冷时间点的温度场,其结果如图10所示. 图10 初期支护和二次衬砌交界面温度与洞内风速的关系 Fig.10Temperature on the interface of primary lining and secondary lining versus wind speed 由图10可知:随着洞内风速的增加,隧道初期支护与二次衬砌交界面的最低温度逐渐降低,因此隧道所需的保温层铺设长度逐渐增大.若洞内风速大于2 m·s-1,在一年中的最冷时间点,隧道衬砌之间的温度将全部降到0 ℃以下,此时保温层需沿隧道纵向全长铺设. (1)依据隧道温度场解析解提出了寒区隧道保温层铺设长度的计算方法,相比现有计算方法,其考虑了隧址区地理地质条件、隧道衬砌厚度及热物理性质、隧道初始温度场及隧道沿纵向的埋深,考虑了洞内空气风速,能针对不同冻土区隧道计算出相应的保温层设计长度. (2)针对处于季节冻土区的白茫雪山1#隧道,计算得到在隧道进口段长2 121 m、出口段长2 619 m铺设5 cm厚保温层能保证隧道衬砌背后排水系统不冻结.针对处于多年冻土区的姜路岭隧道,需在隧道全长铺设5 cm厚保温层才能保证隧道多年冻土段不融化,非冻土段不冻结. (3)通过对地温梯度、洞内风速的敏感性进行分析得出,随着地温梯度的增加,隧道所需的保温层铺设长度逐渐减小,减小幅度可达50%,因此在设计时应根据勘测得到的隧址区地温梯度进行计算.隧道洞内风速对保温层铺设长度的影响十分显著,在设计时应综合考虑隧道通风的要求,尽量降低风速. (4)目前,因为缺乏贯通运营隧道实测数据,由该方法的计算所得长度的保温层的铺设效果还有待进一步检验.另外,由于假定空气在隧道内沿纵向单向流动,该方法适用于自然通风或射流式纵向通风隧道,对于采用横向通风或平行导坑通风的隧道,其保温层铺设长度计算方法有待继续探索和论证. [1]乜风鸣. 寒冷地区铁路隧道气温状态[J]. 冰川冻土, 1988, 10(4): 450. Nie Fengming.Dynamic state of air temperature in railway tunnel in cold regions[J]. Journal of Glaciology and Geocryology, 1988, 10(4): 450. [2]吴紫汪, 赖远明, 藏恩穆, 等. 寒区隧道工程[M]. 北京:海洋出版社, 2003. WU Ziwang, LAI Yuanming, ZANG Enmu,etal. Tunnel engineering in cold region [M]. Beijing: China Ocean Press, 2003. [3]孙文昊. 寒区特长公路隧道抗防冻对策研究[D]. 成都: 西南交通大学, 2005. SUN Wenhao.Study on frostresisting and antifreezing strategies of extra-long highway tunnel in cold area [D].Chengdu:Souhtwest Jiaotong University, 2005. [4]张德华, 王梦恕, 任少强. 青藏铁路多年冻土隧道围岩季节活动层温度及响应的试验研究[J]. 岩石力学与工程学报, 2007, 26(3): 614. ZHANG Dehua, WANG Mengshu, REN Shaoqiang. Experimental study on temperature and response of seasonal active layer of tunnel’s surfounding rock in permafrost region on Qinghai-Tibet plateau [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 614. [5]张先军. 青藏铁路昆仑山隧道洞内气温及地温分布特征现场试验研究[J]. 岩石力学与工程学报, 2005, 24(6): 1086. ZHANG Xianjun. Field experiment on distribution characters of air temperature and ground temperature in Kunlunshan tunnel of Qinghai-Tibet railway [J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(6):1086. [6]陈建勋, 罗彦斌. 寒冷地区隧道温度场的变化规律[J]. 交通运输工程学报, 2008, 8(2): 44. CHEN Jianxun, LUO Yanbin. Changing rules temperature field for tunnel in cold area. Journal of Traffic and Transportion Engineering, 2008, 8(2): 44. [7]赖远明, 喻文兵, 吴紫汪, 等. 寒区圆形截面隧道温度场的解析解[J]. 冰川冻土, 2001, 23(2): 126. LAI Yuanming, YU Wenbing, WU Ziwang,etal. Approximate analytical solution fortemperature fields of a circular tunnel in cold regions [J]. Journal of Glaciology and Geocryology, 2001, 23(2): 126. [8]张耀, 何树生, 李靖波. 寒区有隔热层的圆形隧道温度场解析解[J]. 冰川冻土, 2009, 31(1): 114. ZHANG Yao, HE Shusheng, LI Jingbo. Analytic solutions for temperature fields of a circular tunnel with insulation layer in cold region [J]. Journal of Glaciology and Geocryology, 2009, 31(1): 114. [9]Krarti M, Kreider J F. Analytical model for heat transfer in an underground air tunnel[J]. Energy Conversion and Management, 1995, 37(10): 1561. [10]Kawamura T, Mikami T, Fukumoto K. An estimation of inner temperatures at cold region tunnel for heat insulator design[J]. Kozo Kogaku Ronbunshu A, 2008, 54: 32. [11]夏才初, 张国柱, 肖素光. 考虑衬砌和隔热层的寒区隧道温度场解析解[J]. 岩石力学与工程学报, 2010, 26(9): 1767. XIA Caichu, ZHANG Guozhu, XIAO Suguang. Analytical solution to temperature fields of tunnel in cold region considering lining and insulation layer[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 26(9):1767. [12]戴锅生. 传热学[M]. 北京: 高等教育出版社, 1999. DAI Guosheng. Heat transfer [M]. Beijing: Higher Education Press, 1999. [13]章熙民, 任泽霈, 梅飞鸣. 传热学[M]. 北京: 中国建筑工业出版社, 2007. ZHANG Ximing, REN Zeipei, MEI Feiming. Heat transfer [M]. Beijing: China Architecture & Building Press, 2007. [14]丁靖康. 多年冻土与铁路工程[M]. 北京: 中国铁道出版社, 2011. DING Jingkang. Permafrost and railway engineering [M]. Beijing: China Railway Publishing House, 2011. [15]黑川羲范. ト ンネルつらら防止の現状と問题点[J]. ト ンネルと地下, 1980, 11(12): 13. [16]汪新文. 地球科学概论[M]. 北京: 地质出版社, 2005. WANG Xinwen. An outline of earth sciences[M]. Beijing: Geological Publishing House, 2005. An Approach for Determining Length of Insulation Layer in Cold Region Tunnels XIA Caichu1, FAN Dongfang1,2, LI Qiang1, HE Jia1,3 (1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. China Railway Siyuan Survey and Design Group Co., Ltd, Wuhan, 430063, China; 3. Sichuan Provincial Transport Department Highway Planning, Survey, Design And Research Institude, Chengdu 610041, China) Temperature field is required to be known when designing the insulation layer length of tunnels in cold region at present. To overcome the lack of measured temperature data inside the tunnel, this paper presents an approach for insulation layer length on the basis of temperature field analytical solution which is derived from inlet and outlet weather conditions and terrain conditions. Due to the equal of temperature amplitude that is subjected to the meteorological parameters, the critical length is obtained. When the distance from tunnel entrance is less than critical length, inlet meteorological parameters are adopted to calculate surrounding rock and lining temperature filed in tunnel inlet section. Otherwise outlet meteorological parameters are used. Moreover, the length of insulation layer is determined by the position where 0℃ is occurred on the interface of primary lining and surrounding rock. With the help of insulation layer, the convection heat transfer between air and surrounding rock has changed. Since energy flowing into the surrounding rock in the two cases is equal, the correction coefficient of insulation layer length is confirmed. Combined with the actual project, the length of insulation layer is calculated by the proposed approach. In addition, the influence of the critical parameters (temperature gradient, wind speed) on temperature field is analyzed. The research results show that the needed length of insulation layer decreases as the geothermal gradient increases, and the narrows can be up to 50%, while it increases rapidly as wind speeds up. tunnels in cold region; length of insulation layer; temperature fields; geothermal gradient; wind speed in tunnels 2015-05-05 国家科技支撑计划项目(2014BAG05B05);国家自然科学基金面上项目(41472248) 夏才初(1963—),男,工学博士,教授,博士生导师,主要研究方向为隧道、地下建筑工程、岩石力学等. E-mail:tjxiaccb@126.com U452 A
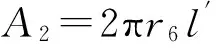
3 实例计算

4 参数分析
5 结论
