载机扰动下SAR/GMTI旋转目标微多普勒特性分析*

耿志高，陈华杰，林萍

（杭州电子科技大学通信信息传输与融合技术国防重点学科实验室，杭州310018）

载机扰动下SAR/GMTI旋转目标微多普勒特性分析*

耿志高，陈华杰，林萍

（杭州电子科技大学通信信息传输与融合技术国防重点学科实验室，杭州310018）

目标微动部件激励的雷达微多普勒信号稳定而独特，反映了该目标的本质特征。针对采用相位中心偏置技术（DPCA）的SAR/GMTI系统，研究存在载机扰动下的旋转目标的微多普勒特性。构建飞行平台与微动目标的几何模型，推导旋转目标的微多普勒信号模型，分析典型的载机纵向扰动对微多普勒时频特性构成的影响；并通过仿真实验，验证了上述理论分析的正确性。

SAR/GMTI，相位中心偏置，载机扰动，微多普勒

0　引言

雷达目标除质心平动以外的微小运动称作微动。目标微动对雷达回波产生附加的频率调制，称为微多普勒效应［1］。微多普勒效应稳定而独特，它为目标识别与目标分类提供了新的途径［2-4］。然而，目标微动信号相较于目标主体信号较弱，尤其对于机载SAR/GMTI系统，回波信号中包含大量地面静杂波，对提取与分析目标的微动信号特性构成严重干扰。

相位中心偏置技术（DPCA）简单易用，是一种可有效抑制地面静杂波技术。文献［5］提出了一种改进的三通道DPCA处理技术，并采用仿真实验进行了验证。文献［6］基于DPCA，分析了在背景杂波环境下提取地面振动目标的微动特性。目前，基于DPCA双通道机载SAR/GMTI系统的研究大多假设载机平台处于平稳飞行下［5-8］，忽略了载机飞行过程纵向扰动对目标微多普勒特性影响。实际中，载机平台飞行过程中极易受到气流影响，导致载机平台飞行中存在纵向扰动。载机纵向扰动导致雷达各孔径在收发信号前后，纵向位置不一致。从而，载机纵向扰动很可能影响目标微多普勒回波特性。故研究载机飞行过程中，纵向扰动对雷达目标回波微多普勒特性的影响，具有十分重要的现实意义。

本文针对载机运动过程中存在的纵向扰动，通过建立旋转目标微多普勒回波信号模型，研究了纵向扰动对旋转目标微多普勒特性的影响。仿真模拟了载机扰动在不同角频率和幅值下，对旋转目标微多普勒回波信号的影响。最后通过仿真实验数据与公式计算所得数据比较，验证了分析的正确性。

1　机载SAR双通道建模分析

1.1双通道SAR/GMTI工作示意图

如图1所示，此处雷达天线采用单发双收，即全孔径天线发射信号，其余两个子孔径天线进行接收信号，以正侧视方式工作。其中D0为发射天线相位中心，D1、D2为两个接收信号的子孔径。各孔径间距为B。假设载机飞行高度为H，水平运动速度为v，沿Y轴正方向，纵向扰动为简谐振动c sin（Ωt）。

图1　双通道SAR/GMTI工作示意图

1.2旋转目标回波信号分析

假设散射点P在yoz平面以o为圆心作半径为r的匀速圆周运动，其中o点坐标（x0，y0，z0）。点P旋转角频率为ω，初始相位为θ。初始时，全孔径中心D0的坐标为（0，vt，H+c sin（Ωt）），子孔径D1与D2中心坐标分别为（0，vt-B，H+c sin（Ωt））、（0，vt+B，H+c sin（Ωt））。散射点P坐标为：

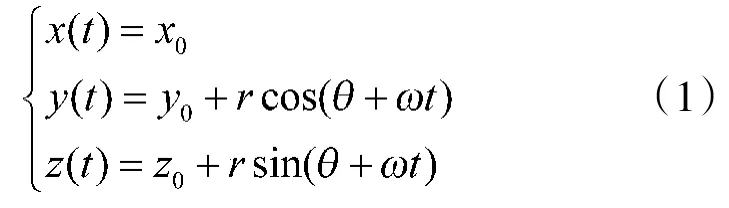
全孔径相位中心D0到散射点P的斜距R0（t）为：

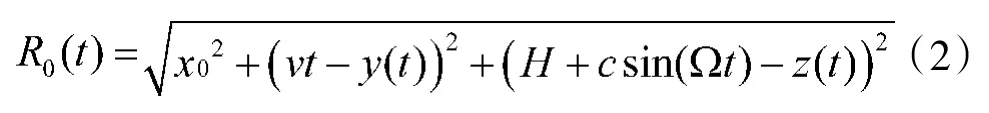
按照式（3）

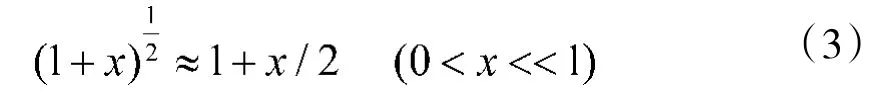
同理可得D1、D2到点P的斜距R1（t）、R2（t）分别为：

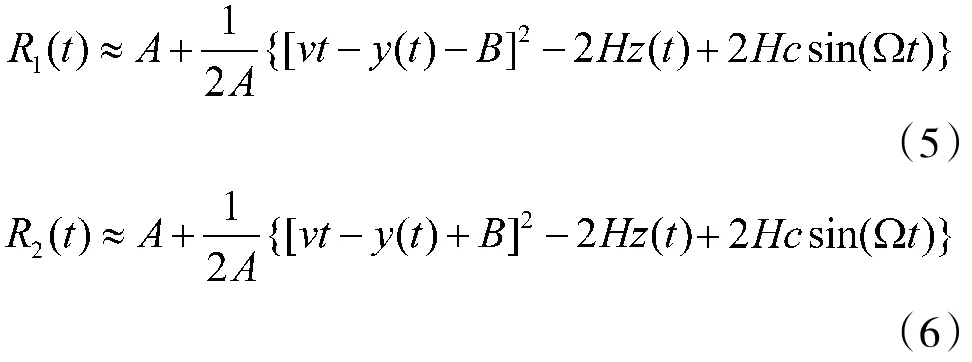
假设P（t）为雷达发射的线性调频信号，即：

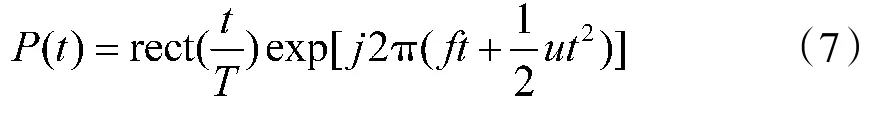
式（7）中，当-1/2≤t≤1/2时，rect（t）=1；当t＜-1/2或t＞1/2时，rect（t）=0。其中f表示雷达信号载频，T为雷达信号脉冲宽度，u为雷达信号线性调频率，t为距离向快时间。则双通道回波信号经过相干检波和距离压缩后，转换为基带信号为：

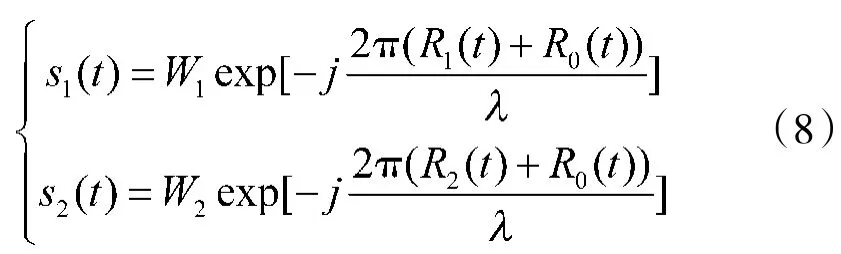
式（8）中，W1和W2为常数项，由散射点的后向散射系数与天线的方位向图共同决定。此处假设两个通道的回程方向图一致，则可记W1=W2=W。接下来补偿由各子孔径相位中心间隔引起的多普勒中心调频率偏差，以及载机水平运动产生的多普勒频率线性调频项［9］。用作双通道基带信号相位补偿的参考函数［10］分别为：

记基带信号与其对应的补偿函数相乘后的信号分别为s1'（t）和s2'（t），再对处理后的信号进行时间校准以抑制静杂波信号。其中，相邻孔径间距B，载机速度和雷达信号脉冲重复频率prf，三者需满足关系式B=2nv/prf（其中n为正整数）。

2　载机扰动对微多普勒特性影响分析

2.1载机扰动对DPCA处理影响

为简化分析过程令θ=0。由以上各式可得：

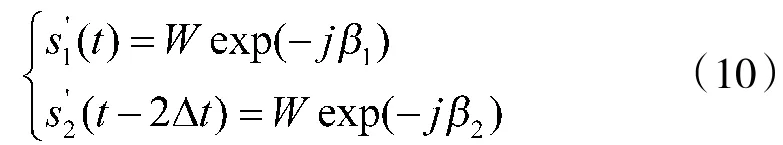
式（10）中：

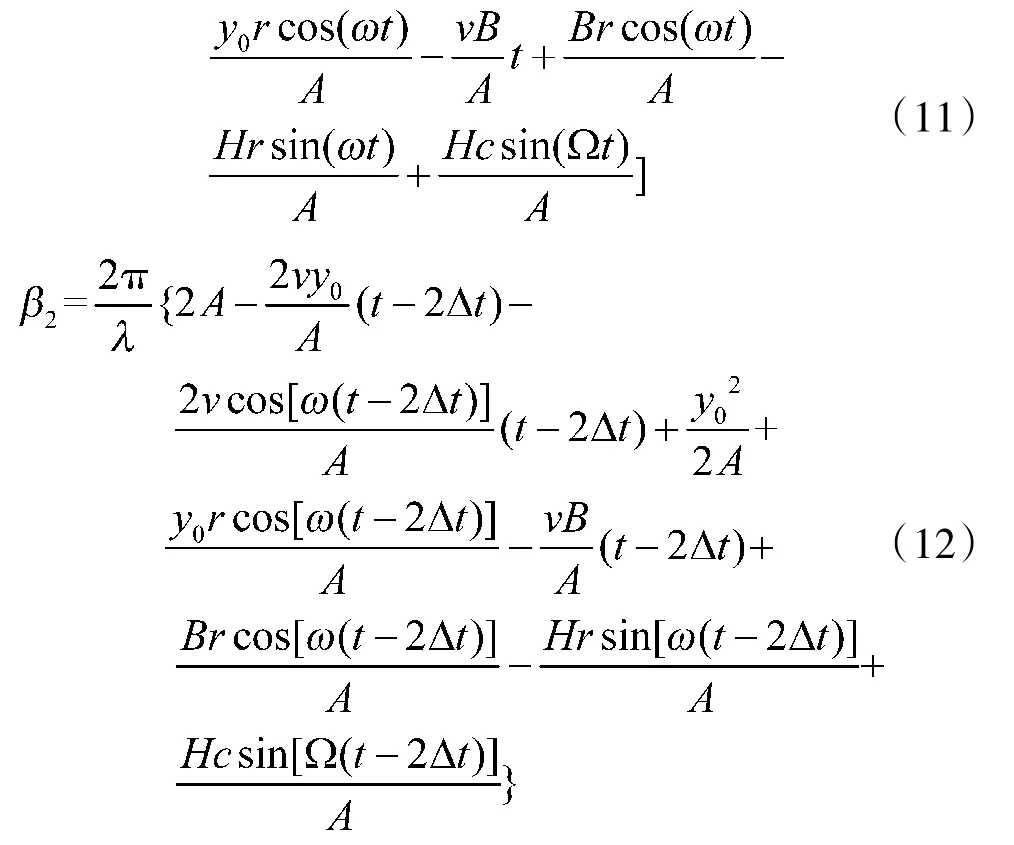
双通道对消后，可得：

式（13）中：

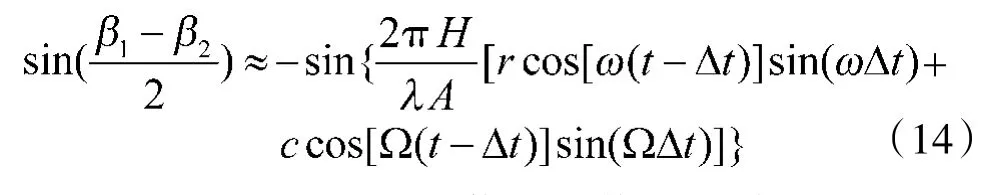
式（14）为目标回波信号幅值。对其分析可知，目标回波信号幅值经过双通道对消后由两部分构成，一部分由目标自身所激励，另一部分由载机的扰动所产生。当载机不受纵向扰动干扰，即c和Ω均为零。此时，对于静止目标和雷达背景，其ω和r均为零。表明静止目标和雷达背景回波信号经过DPCA处理后，信号幅值为0，即静止目标与背景信号均被滤除。而对于旋转目标，其ω和r均不为零。故其信号幅值亦不为0，说明经DPCA处理后，目标微动信号得以保留。

当载机受到纵向扰动干扰，此时回波信号经DPCA处理后，虽能滤除静止目标与雷达背景信号，可由于载机纵向扰动所产生的影响无法被消除，致使目标微多普勒特性受到影响。

2.2载机扰动对旋转目标微动特性影响

接下来，着重分析载机纵向扰动对旋转目标微动特性的影响。从式（13）中可得旋转目标回波信号相位为：

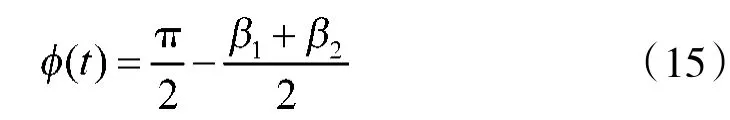
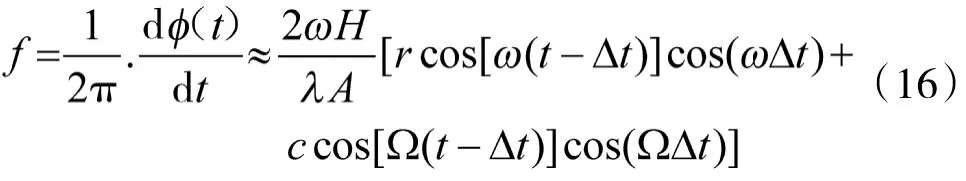
式（16）即为载机平台受到纵向扰动时，旋转目标瞬时微多普勒表达式。由式（16）可知：

（1）旋转目标微多普勒由两项叠加组成。第一项分量由目标旋转激励产生，第二项分量由载机纵向扰动产生。其中，目标自旋激励部分，由于假设目标作圆周运动，故其微多普勒分量按余弦函数规律变化。载机纵向扰动所激励部分实际也是由载机扰动形式所决定，由于此处假设载机纵向扰动为简谐振动，故这一分量也作余弦规律变化。

（2）旋转目标微多普勒的频率由ω和Ω共同决定。由相关三角函数知识可知，当ω和Ω相近时，载机扰动对微多普勒频率影响较小。但ω和Ω相差较大时，载机扰动对微多普勒频率影响较大。

（3）旋转目标微多普勒的幅值由r和c共同决定。当载机扰动幅值相较于目标旋转半径较小时，特别对于较大旋转半径目标，如直升机的旋翼，此时载机轻微扰动的影响几乎可忽略。但当载机飞行中发生剧烈起伏和旋转目标半径较小时，如装甲车的车轮和履带，此时载机扰动所产生的干扰与旋转目标微多普勒回波信号相互叠加，使得旋转目标的微多普勒信号被掩盖。

3　实验验证分析

仿真实验中，SAR/GMTI雷达平台主要参数如表1，雷达采用C波段机载SAR，按照图1天线配置方式。仿真场景中，目标坐标（3 000，0，0.6）；目标旋转半径r=0.6m；目标旋转角频率ω=24 rad/s。为验证载机扰动角频率对微多普勒特性的影响，仿真实验中将载机扰动幅值设为c=0.1m，实验得出载机扰动角频率分别为Ω=36 rad/s和Ω=64 rad/s时旋转目标微多普勒时频图，即图2所示。

表1　仿真实验主要参数

图2　载机不同扰动角频率旋转目标微多普勒回波时频图

由于所设载机扰动幅值相较于目标旋转半径较小，当载机扰动角频率与目标旋转角频率相近时，由图2（a）可见，此时载机扰动对旋转目标的微多普勒信号影响较小，其微多普勒曲线形状与余弦函数相近。但随着载机扰动角频率增加，由图2（b）可见，旋转目标微多普勒曲线受到的干扰加剧，微多普勒曲线出现了许多小的波峰与波谷。

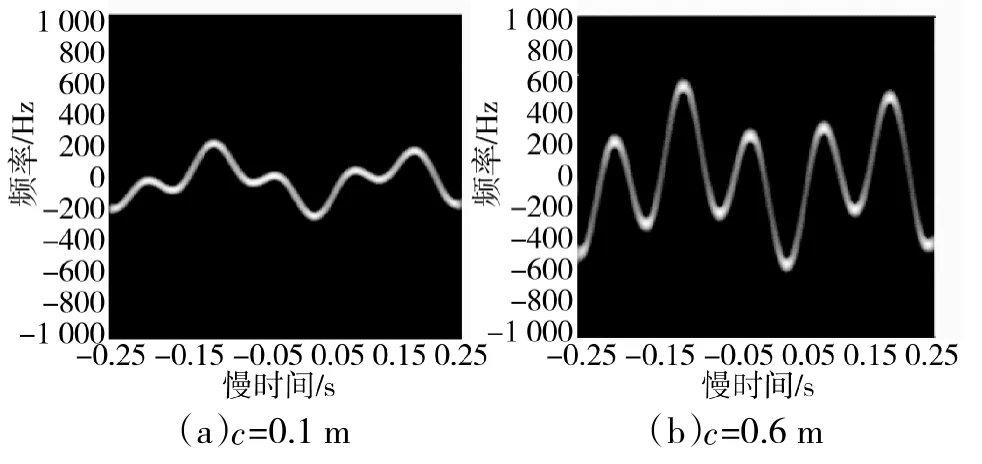
图3　载机不同扰动半径旋转目标微多普勒回波时频图

为验证载机扰动幅值对旋转目标微多普勒特性的影响。基本实验参数同前，将载机扰动角频率设为Ω=64 rad/s，分别得出载机扰动幅值为c=0.1m和c=0.6m时旋转目标微多普勒时频图，即图3。

由图3（a）和图3（b）可知，当载机扰动幅值增大至目标旋转半径时，扰动分量干扰加剧，以致旋转目标微动特性被完全掩盖。

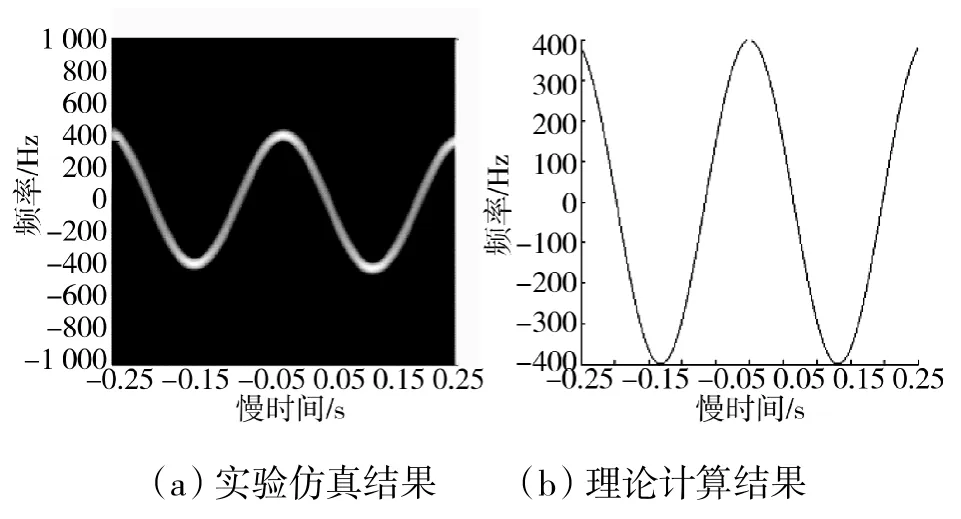
图4　旋转目标微多普勒时频图与理论计算结果

通过比较旋转目标微多普勒时频图和理论计算结果，验证理论推导的正确性。为使实验结果直观易于比较，选取旋转目标旋转半径r=0.6m，角频率ω=24 rad/s，载机飞行扰动幅值c=0.6 m，角频率Ω=24 rad/s。图4（a）为旋转目标微多普勒时频图。由于选取载机扰动参数与旋转目标旋转运动参数一致，根据式（16）及三角函数相关知识可知，其图像由两个分量余弦函数幅值相加，角频率不变。由图中可见，其微多普勒信号按余弦规律变化，与前面分析相吻合。还可看出，其微多普勒信号的最大多普勒平移约为400 Hz，旋转周期约为0.25 s（即ω=25 rad/s）。图4（b）为根据式（16）计算所得载机扰动下旋转目标微多普勒时频图。对比图4（a）与图4（b）可知，载机扰动下经双通道DPCA处理后，旋转目标微多普勒时频图与理论计算所得结果一致，从而验证理论推导的正确性。

4　结论

本文通过构建双通道SAR/GMTI载机平台与旋转散射点模型，经理论推导，最后通过仿真实验，得出如下结论：

（1）在SAR/GMTI系统下，双通道回波信号经DPCA处理后，旋转目标回波微多普勒信号会由载机纵向扰动而增加一附加项。该附加项与载机扰动幅值、角频率、运动形式相关。

（2）载机扰动对目标微动特性影响程度，不仅与载机扰动幅值和角频率相关，还与旋转目标自身微动参数相对大小有关。当载机剧烈起伏或旋转目标运动，旋转目标微多普勒信号将被掩盖。

［1］CHEN V C，LI F，HO S S，et al.Micro-Doppler effect in radar：phenomenon，model，and simulation study［J］.IEEE Transactions on Aerospace and Electronic System，2006，42（1）：2-21.

［2］KIM Y，LING H.Human activity classification based onmicro-Doppler signatures using a support vector machine［J］. IEEE Transactions on Geoscience and Remote Sensing，2009，47（5）：1328-1337.

［3］RAM SS，CHRISTIANSONC，KIM Y，etal.Simulation andanalysis of human micro-Dopplers in through-wall environments［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48（4）：2015-2023.

［4］李彦兵，杜兰，刘宏伟，等.基于微多普勒效应和多级小波分解的轮式履带式车辆分类研究［J］.电子与信息学报，2013，35（4）：896-900.

［5］张佳佳，周芳，孙光才，等.基于机载前向阵雷达的三通道SAR-GMT技术研究［J］.电子与信息学报，2012，34（2）：344-350.

［6］张伟，童创明，张群，等.基于DPCA杂波抑制的地面振动目标微多普勒提取［J］.系统工程与电子技术，2011，33（4）：738-741.

［7］杨贤林，沈汀.机载双通道SAR/GMTI数据域DPCA算法研究［J］.现代雷达，2006，28（4）：29-33.

［8］韦北余，朱岱寅，吴迪.基于杂波对消-自聚焦的多通道SAR-GMTI［J］.航空学报，2015，36（5）：1585-1595.

［9］张伟，童创明，张群，等.基于时频分析的双通道SAR自旋目标检测［J］.航空学报，2011，32（10）：1914-1923.

［10］康雪艳，杨汝良.多通道SAR杂波抑制技术研究［J］.遥感技术与应用，2005，20（1）：206-210.

M icro-Doppler Analysisof a Rotating Target in SAR/GMTI w ith Aircraft Disturbance

GENG Zhi-gao，CHENHua-jie，LIN Ping
（Key Laboratory of Fundamental Science for National Defense Communication Information Transmission and Fusion Technology，Hangzhou Dian ziUniversity，Hangzhou 310018，China）

The micro-Doppler modulation induced by micro-mechanical structures is stable and unique，which can reflect the unique feature of the target.According to SAR/GMTIsystem adopting the Displaced Phase Center Antenna（DPCA）method，the rotating target of themicro-Doppler feature with aircraft disturbance is researched on.Constructing themodel of the aircraft and target，themodel of the rotating target is derived，the aircraft disturbance’s influence on the rotating target’s micro-Doppler feature is analyzed.At last，the correctness of the analysis are proved by simulation results.

SAR/GMTI，displaced phase centerantenna，aircraftdisturbance，micro-Doppler

TN957

A

1002-0640（2016）09-0046-04

2015-07-13

2015-08-12

“十二五”国防预研基金资助项目

耿志高（1988-），男，河北唐山人，硕士研究生。研究方向：SAR雷达目标识别。