丰富直观经验培养空间观念
2016-10-17祝浩军
摘 要:在几何图形教学中,教师往往以讲代做,强调记住名称或规则,学生缺少动手操作和丰富的直观经验,从而导致空间与图形方面问题解决中出现错误。设计一些让学生熟悉从平面到立体的转换过程的操练性作业,让学生自主直观地去探究几何形体的性质及关系,有利于培养学生的空间观念和几何直观。
关键词:空间观念;直观;操作;案例研究
中图分类号:G623.5 文献标识码:B 收稿日期:2016-05-04
作者简介:祝浩军(1973—),男,浙江上虞人,中学高级教师,浙江省绍兴市上虞区实验小学副校长,曾被评为浙江省绍兴市上虞区优秀专业技术人才。
一、直面错题
在小学阶段,学生经常会遇到这些数学问题:①至少用几个相同的小正方形,又能拼成一个大一些的正方形?②至少用几个相同的小正方体,才能拼成一个稍大一些的正方体?
这两个数学题目,不管是低年级学生还是高年级学生,都常常会出错:第一题做成2个,第二题认为至少用4块相同的小正方体。而且不少数学老师给学生讲了正确答案后,个别学生对同类型的问题还是出错。
在一次区小学五年级数学期末质量检测卷中出现了一个同类型的考查学生空间与图形方面问题解决的试题,难度基本相同。试题如下。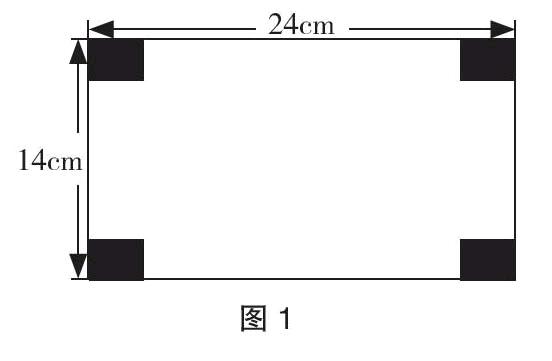
张芳有一块长方形硬纸板(如图1),她打算做一个粉笔盒:从四个角各剪去一个边长为4cm的正方形,然后粘成一个粉笔盒。①这个粉笔盒共用了多少硬纸板?请你写出解题过程。②这个粉笔盒的容积有多大?③你还有其他制作方案吗?请你也做一个。(这小题选做)
笔者调查了3所乡镇小学的每个学校各1个班级学生的测试题,整题列式正确,计算失误按正确计;分步列式,计算错误,或面积单位与体积单位搞错,按答错计。统计发现,此题的整体正确率在87%左右,但班级与班级之间正确率的差距非常明显,有的班级的错误率达到44%。看似简单,错误率却高,原因何在?如何更好地帮助学生从平面思维到立体思维过渡,正确解决这类问题,培养学生的空间观念呢?
二、调查分析
首先,分析学生学习上的困难。学生对从平面图形的周长与面积计算与理解逐步过渡到立体图形的表面积计算、体积计算,一时很难接受,甚至会出现思维上的断裂。形象思维能力的培养与发展需要借助实物,学生面对缺少实物支撑的空间大小、表面积多少等实际问题就会束手无策。空间观念、空间想象能力差的学生理解不了,就不会解决实际应用问题。
其次,调查访问任课教师。正确率相对较高的五年级数学老师认为,教师帮助学生从平面思维过渡到立体思维的过程教学是否让学生有真切的体验是很重要的。特别是在“长方体和正方体的认识”一节的教学中,需要让学生“玩”长方体、正方体,动手做一做、拆一拆纸盒。因为这节课是学生对图形认识的一个转折点,它从平面图形过渡到立体图形,从计算面积到计算体积,对于学生空间观念的发展来说,是一个质的飞跃。部分数学老师没有认识到这一点,以自己的讲解、演示代替了学生的操作与思考。
最后,分析评估日常课堂教学。笔者大胆猜测,学生试题错误率高的教师在平时的教学中,总是以完成教学任务为主要目的,不充分考虑学生的年龄特点、认知规律;在创设操作情境,尽可能给学生提供动手操作的机会方面明显不足。有些空间图形的问题解决没有让学生自己动手做,而是以讲代做,学生没有获得真切、可信的图形知识。与几位任课教师的交谈与反思证实了笔者的猜测。
三、寻求改进
心理学研究证明:儿童的思维是从动手开始的,切断活动与思维的联系,思维就不能得到发展。下面以“长方形硬纸板做成粉笔盒”的问题为例,谈如何让学生在从“平面”到“立体”的转换中培养空间观念的教学策略。
第一,提供直观,动手操作。即让每个学生动手做纸盒子,让学生人人拿把剪刀、浆糊或透明胶,粘长方体、正方体。学生通过做,经历剪去四个角、将棱边胶合在一起的过程。做成这个纸盒,用剪刀剪过四个小正方形,孩子脑中一定会印象深刻。“听过了我忘记了,看过了我记住了,做过了我理解了!”要使学生在学习比较抽象的数学知识时感兴趣,对知识理解透彻,就要让学生多动手操作,这有助于学生建立表面积的概念。同时,学生操作的顺序性促进学生语言的条理性和整体性的提升。
第二,引导分析,弄清概念。原先的一块长方形纸板,剪去四个角上的正方形后,在拼成长方体的过程中,什么发生了变化?这个纸盒的长、宽、高分别是多少?四角剪去长方形行吗?为什么?让学生动手添辅助线,再启发学生思考:请你画一画虚线,指一指,算一算做成盒子后的底面、前面与左侧面各是多少平方厘米?让学生建立好几何概念的直观模型,弄清几何的关系、几何的变换,使知识更有条理性,空间想象能力更好,解决问题的能力更强。
第三,鼓励质疑,促进反思。数学知识本身是枯燥、抽象的,要解决数学知识的抽象性和学生思维的形象性之间的矛盾,关键是动手操作,以直观的形式展现在求知者前面,如牙膏盒、魔方、药盒等物体,通过看一看、量一量、比一比发现长方体面、棱、顶点的特征,感受学习的乐趣。同时,要让学生自己提问题,哪些部分思考过程还没有搞懂,有些什么疑问。学生质疑与教师教学的有机结合,引导学生将自己心中的疑问说出来,让学生的空间认知更明晰,解决实际图形问题更有思路。
四、举一反三
学生的几何思维与学习历程通常都源自一定的视觉或操作的直观经验,几何概念的抽象定义是后来才赋予的,因此学生对几何图形的辨识需要通过动手操作、观察、再动脑、思考,从“平面的二维思维”过渡到“立体的三维思维”,丰富直观经验,发展学生的空间观念。例如,在学习了“圆柱与圆锥”后,我们应该让学生做一做这些习题,巩固知识,发展空间观念。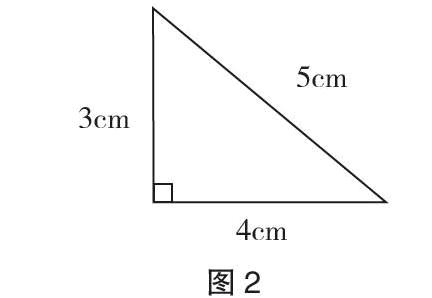
图2是一个直角三角形,两条直角边的长分别是3厘米和4厘米。把该三角形以一条边为轴进行旋转,旋转的轨迹可以形成一个立体图形,以3厘米的直角边为轴旋转,可以得到一个怎样的立体图形? 还能用其他的办法旋转吗?分别得到怎样的立体图形?请你动手做一做,并求出各个立体图形的体积。(圆周率取3.14)
通过这些问题、习题的操练,为学生的空间直观提供机会与支架,如果只是教师传授、讲解甚至只讲答案,学生的空间观念培养和空间思维发展必将是有限的、枯燥的。因此,我们要为学生提供丰富的直观空间图形,重视直观模型的建立,让学生经历动手操作、分析、质疑的过程,培养学生的空间观念,促进学生的思维发展。
参考文献:
[1]鲍建生,周 超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009.
[2]宋乃庆,张奠宙.小学数学教育概论[M].北京:高等教育出版社,2006.
