一类非线性六阶波动方程的几乎守恒律

王宏伟

（安阳师范学院数学与统计学院，河南安阳 455000）

一类非线性六阶波动方程的几乎守恒律

王宏伟

（安阳师范学院数学与统计学院，河南安阳 455000）

研究了一类非线性六阶波动方程的Chaucy问题，通过引入一个修正的能量泛函，借助Airy方程的Strichartz估计，在Bourgain空间中证明了这类方程的几乎守恒律.

修正的能量泛涵；几乎守恒律；Bourgain空间

在研究具有表面张力的浅水波表面的毛细管重力波传播问题时，Daripa和Dash［1］提出了如下的非线性六阶波动方程

这里u（x，t）是未知函数，φ（x），ψ（x）是已知的初始函数，下标t，x分别表示对t，x求偏导数，f（u）是非线性项，β＝±1.方程（1）也可以作为弹性晶体中晶格动力学问题的数学模型［2］.

当非线性项f（u）＝u2时，Esfahani［3］研究了方程（1）局部解的适定性问题，即解的存在性、唯一性和解对初值的连续依赖性；Wang［4］讨论了周期解的适定性问题.对非线性项f（u）＝｜u｜2u，Wang［5］利用I－能量方法证明了当初值（φ，ψ）∈Hs×Hs－1，3／2＜s＜2时方程（1）整体解的适定性.

对更一般的非线性项f（u）＝｜u｜2ku，k≥1，k∈Z，方程（1）具有下面的能量守恒律［6，7］

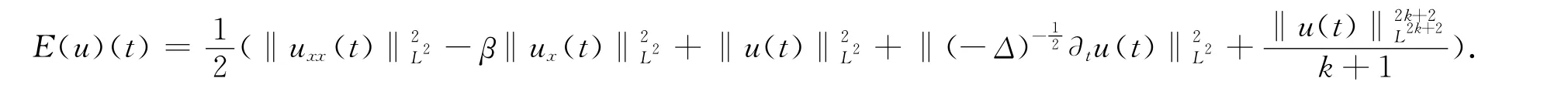
当初值（φ，ψ）∈Hs×Hs－1，s≥2时，利用局部解的存在性和守恒律就可以得到方程（1）整体解的适定性.当初值的正则性指标s＜2时，能量可能是无穷大，此时守恒律没有意义.本文的主要目标是引入一个修正的能量泛函，并在初值的正则性指标1／2＜s＜2的条件下，证明这个能量泛函是几乎守恒的.随着时间的增大，该能量泛函可以得到控制，由此可以把局部解的存在区间延拓到任意的时间T，从而得到整体解的适定性.

1　预备知识

u（x，t）的时空Fourier变换定义为u∧（ξ，τ）＝∫R2e－i（xξ＋tτ）u（x，t）dtdx.对s∈R，Hs（R）表示通常的Sobolev空间，它的范数定义为‖f‖Hs＝‖〈ξ〉f∧（ξ）‖L2，其中〈·〉＝1＋｜·｜，记LqtLrx为混合时空范数

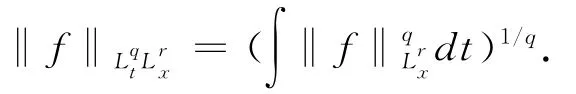
定义1 对s，b∈R，记Xs，b为Schwartz函数类在下列范数下的完备化空间

根据定义1，有如下范数的等价形式

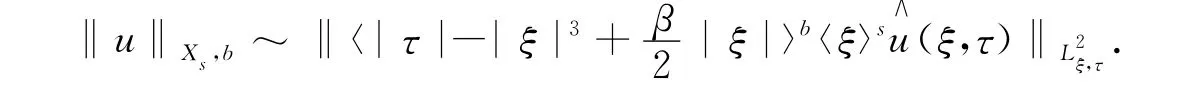
利用Kato的光滑性估计［9］，有

由定义1直接可以得到

（4），（5）两式利用插值定理，有

使用最大值函数的估计，还可以得到

下面我们给出一个新的修正的能量泛函.给定s＜2和一个常数N》1，定义乘子I为

把算子I作用到方程（1），（2）两边，得到

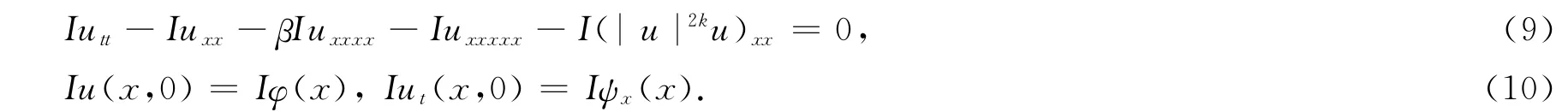
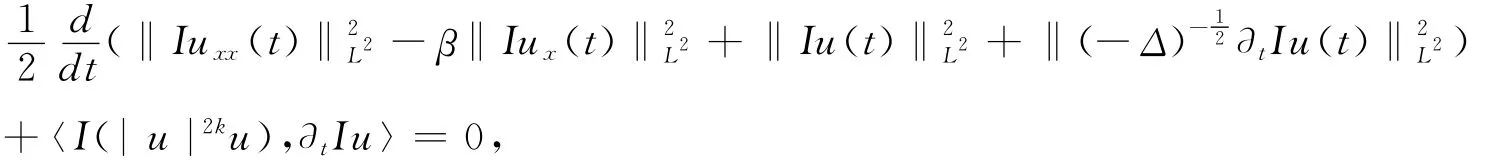
合并以上两式，得到

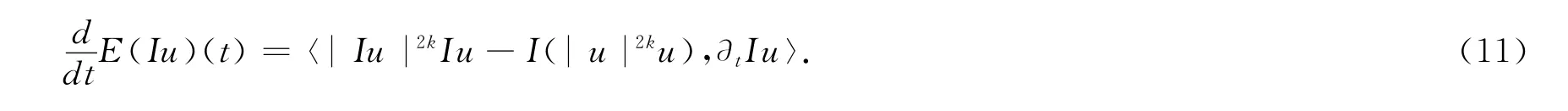
2　主要结论

下面的定理说明，随着时间的增大，E（Iu）（t）是几乎守恒的.

定理 假定s＞1／2，N》1，Iu是（9）定义在［0，δ］上的解，则下列估计成立

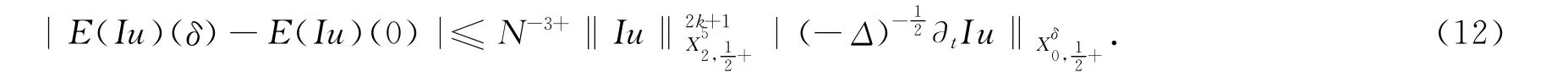
证明 等式（11）两边在［0，δ］上对t积分，再应用Parseval公式，得到

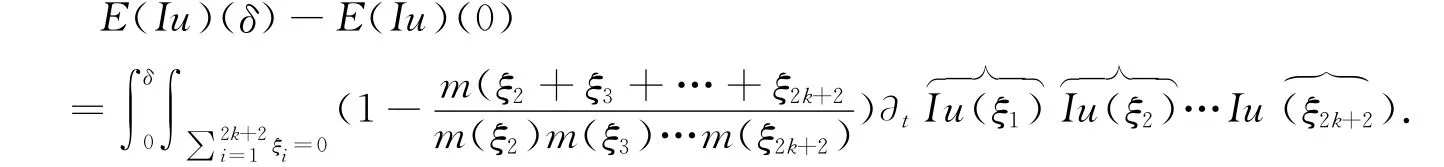
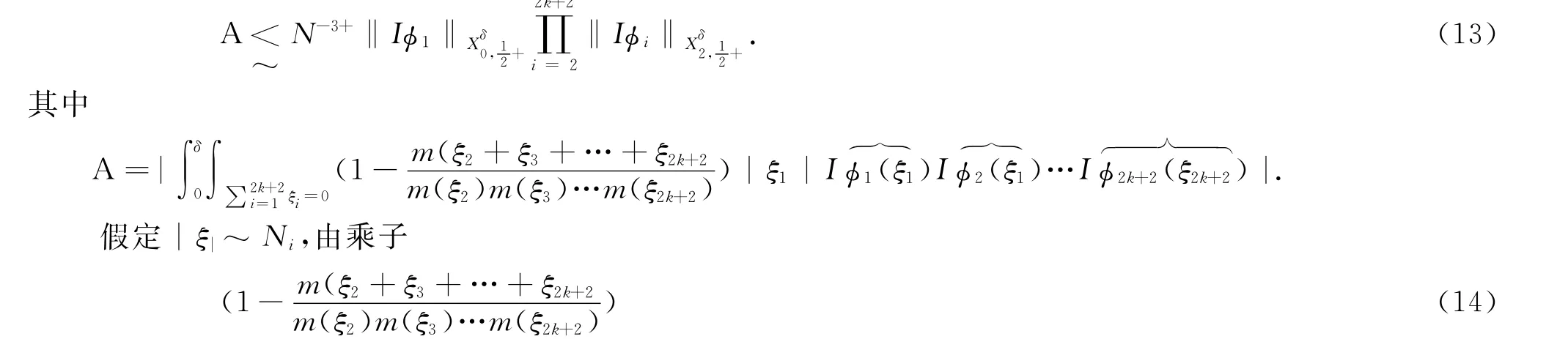
要得到（12），只须证明下列不等式成立关于ξ2，ξ3，…，ξ2k＋2的对称性，不妨假定N2≥N3≥…≥N2k＋2.由于，故下面我们通过比较N和Ni的相对大小，分情况来证明（13）.

情形1：N》N2.此时根据m（ξ）的定义，（14）式的值等于零.（13）成立

情形2：N2＞N》N3.由于＝0，此时可以得到N1～N2.根据中值定理，有

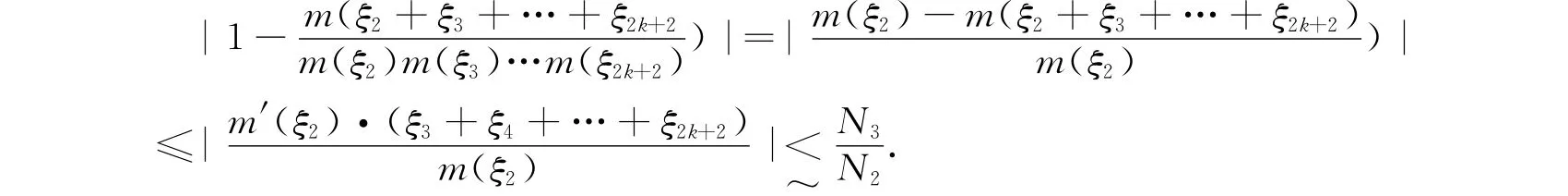
由（6），（7）和Hlder不等式，可知

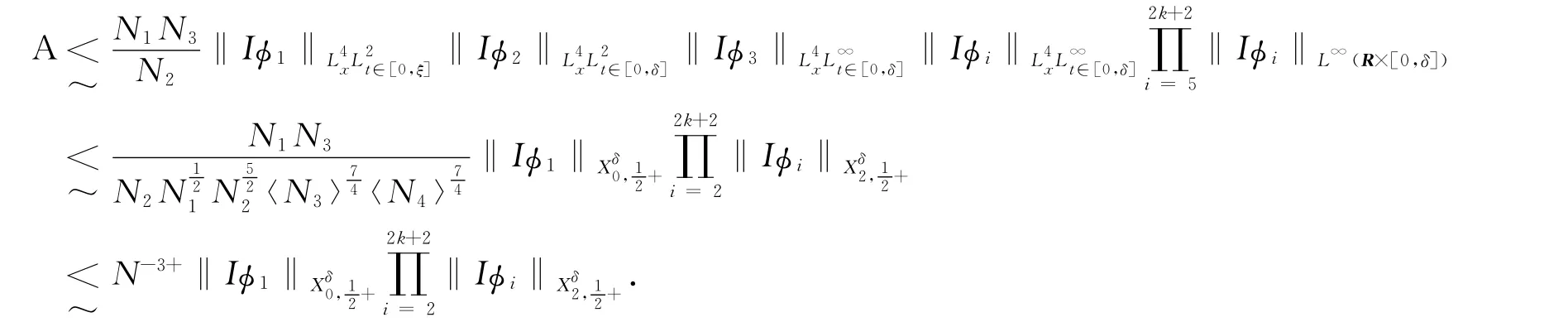
情形3：N2》N3＞N.此时，估计（14）如下

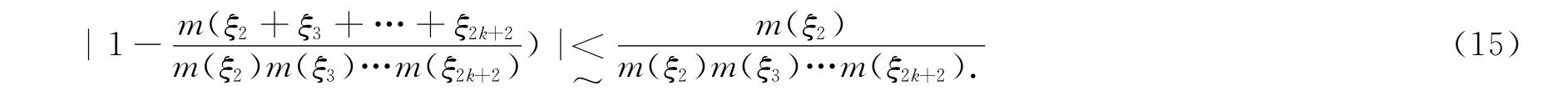
由于m（ξ2）～m（ξ3），得到

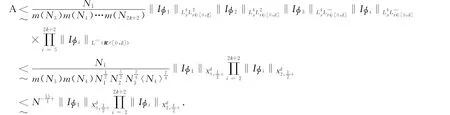
这里最后一个不等式成立是由于对任何p≥2－s，函数m（x）xp是单调增加的，并且m（x）〈x〉p是有下界的，这就表明

（1）N3》.此时A的估计如下

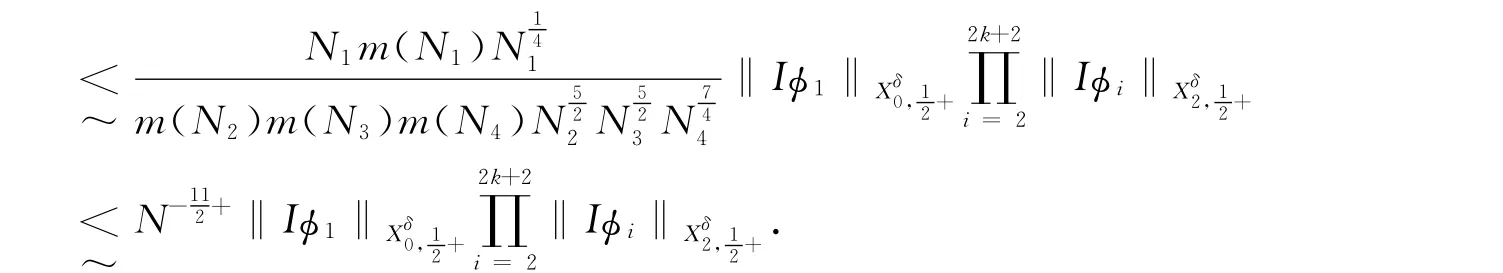
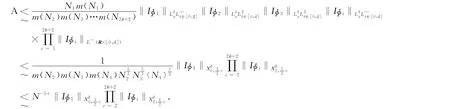
综合以上各种情况，定理得到证明.

［1］ DAPIPAP，DASH R K.Studies of capillary ripples in a sixth－order Boussinesq equation arising in water waves，in：mathematical and numerical aspects of wave propagation［M］.SIAM Philadelphia，2000：285－291.

［2］ MAUGIN G A.Nonlinear waves in elastic crystals［M］.Oxford Mathematical Monographs Series，Oxford，1999.

［3］ ESFAHANI A，FARAH L G.Local well－posedness for the sixth－order boussinesq equation［J］.Journal of Mathematical Analysis and Applications，2012，385（1）：230－242.

［4］ WANG H，ESFAHANI A.Well－posedness for the cauchy problem associated to a periodic boussinesq equation［J］.Nonlinear Analysis TMA，2013，89：267－275.

［5］ WANG H，ESFAHANI A.Global rough solutions to the sixth－order boussinesq equation［J］.Nonlinear Analysis TMA，2014，102：97－104.

［6］ ESFAHANI A，LFVANDOSKYS.Stability of solitary waves for the generalized higher－order boussinesq equation［J］.Journal of Dynamics and Differential Equations，2012，24：391－425.

［7］ ESFAHANI A，FARAHL G，WANG H.Global existence and blow－up for the generalized sixth－order boussinesq equation［J］.Nonlinear Analysis TMA，2012，75：4325－4338.

［8］ KENIG C，PONCE G，VEGAL.On the（generalized）korteweg de vries equation［J］.Duke Math J，1989，59：585－610.

［9］ KENIG C，PONCEG，VEGAL.Wellposedness and scattering results for the generalized korteweg de vries equation via the contraction principle［J］.Commun Pure Appl Math，1993，46：527－620.

The Almost Conervation Law of a Nonlinear Sixth－Order Wave Equation

WANG Hong－wei
（Department of Mathematic and Statistics，Anyang Normal Unversity，Anyang 455000，China）

In this paper，we study the Cauchy problem of a nonlinear sixth－order wave equation.We introduce a new modified energy function.By use of the Strichartz estimates of Airy equation，the almost conservation law of this equation is proved in Bourgain space.

modified energy functional；almost conservation law；Bourgain space

O175.25

A

1001－2443（2016）03－0226－04

10.14182／J.cnki.1001－2443.2016.03.004

2015－04－10

国家自然科学基金（10771166）；河南省教育厅科学技术研究重点项目（14B110028，16A110007）；安阳师范学院培育基金（AYNUKP－B04）.

王宏伟（1977－），男，河南汤阴人，讲师，博士研究生.主要从事调和分析和偏微分方程的研究.

引用格式：王宏伟.一类非线性六阶波动方程的几乎守恒律［J］.安徽师范大学学报：自然科学版，2016，39（3）：226－229.