一种基于椭圆曲线自双线性映射的多秘密共享方案

张尚韬

（福建信息职业技术学院计算机工程系，福建福州350003）

一种基于椭圆曲线自双线性映射的多秘密共享方案

张尚韬

（福建信息职业技术学院计算机工程系，福建福州350003）

分析了DuoLiu等人提出的基于椭圆曲线自双线性映射的多秘密共享方案，发现该方案易遭受分发者/参与者欺诈攻击和广播窃听攻击，并依赖安全信道；提出了一种基于单向散列函数、密钥协商协议和动态多方Deffie-Hellman协议的改进方案,改进方案能抵抗分发者/参与者欺诈攻击和广播窃听攻击，并使方案摆脱对安全信道的依赖.最后对改进方案的安全性进行了分析.

椭圆曲线；自双线性映射；多秘密共享；欺诈攻击；广播窃听攻击

秘密共享就是在一组参与者中共享秘密，它主要用于防止重要信息被丢失、破坏、篡改或落入坏人手里.文献[1]基于Lagrange插值多项式提出一种（t，n）门限秘密共享方案.所提方案存在两方面问题：第一，方案中n个参与者共享一个秘密s，而现实中，常常由n个参与者共享m个秘密，这引起学者对多秘密共享方案的研究[2-3]；第二，方案中默认分发者/参与者是诚实的，这是不现实的，由此学者们提出了可验证的秘密共享方案[4].

Hyang-Sook Lee提出一种有限域椭圆曲线上的自双线性映射算法[5].与同类方案相比，基于此算法设计的公钥密码方案在安全性、灵活性、兼容性、计算消耗、存储消耗和带宽消耗等方面性能优越.基于此算法，Duo Liu等人提出了一种多秘密共享方案[6].分析发现该方案易遭受分发者/参与者欺诈攻击和广播窃听攻击，并依赖安全信道对其进行改进，新方案保留了原有的安全特点，且安全性更高.

1　椭圆曲线自双线性映射

定义设（S，T）为m-挠群E[m]上的一组基.任取P=a1S+b1T，Q=a2S+b2T，R=a3S+b3T，P，Q，R∈E[m]，a1，b1，a2，b2，a3，b3∈[0，m-1]，对于任意整数α，β∈[0，m-1]，α β≠0，E[m]上的自双线性映射定义为：

2）对于任意P，Q，R∈E[m]有

3）对于任意P，Q∈E[m]有，

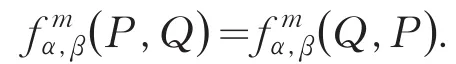
5）如果P∈E[mm′]，Q∈E[m]，那么

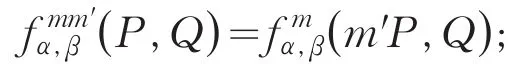
类似地有，如果P∈E[m]，Q∈E[mm′]，那么

2　DuoLiu方案概述及安全性分析

2.1Duoliu方案概述

共享秘密为{M1，M2，…，Mm}，Mi，1≤i≤m是椭圆曲线特定挠群上的点.方案包含四个阶段：初始化阶段，子密钥分配阶段，构造阶段和重建阶段.

2.1.1初始化阶段

D为可信的分发者，{P1，P2，…，Pn}为参与者集合，D在公告栏上发布公开消息.初始化阶段如下：

1）D选定有限域GP（q）上的椭圆曲线E，其中q= pr，p是一个大素数，以使得有限域中椭圆曲线E（GP（q））上的离散对数问题是难解的.随后D选择一个大素数以及E（GP（qk））上的l-挠群E[l]，其中k是一个整数；

3）D在公告栏中公布{E，q，l，k，α，β，G，H}；

2.1.2子密钥分配阶段

1）D计算一个范得蒙矩阵A：

4）D将{aj，bj}，1≤j≤n经过安全信道发送给参与者Pj；

2.1.3构造阶段

参与者{P1，P2，…，Pn}通过一下步骤共享{M1，M2，…，Mm}：

1）对于{M1，M2，…，Mm}⊂E[l]，分发者D为所有的随机选择并计算Qi=

2）D计算并在公告栏上公开ci，di和

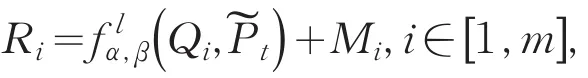
2.1.4重建阶段

假设t个参与者{Pu1，Pu2，…，Put}要重建秘密信息Mi，重建步骤如下：

2）Puj计算Qij=（Qi，Suj），其中

3）Puj将Qij=（Qi，Suj）广播给{Pu1，Pu2，…，Put}

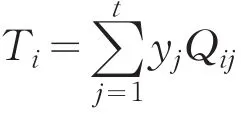
5）Puj计算Mi=Ri+Ti得到秘密Mi.

2.2安全性分析

2.2.1分发者/参与者欺诈攻击问题

在Duo Liu等人的方案中，假设分发者和参与者是诚实的，这是很难满足的.如果分发者D向参与者Puj发送一个虚假的子密钥{aj，bj}，Puj通过计算获得的Qij就是无效的，使得广播后，任何参与者无法通过计算获得正确的Mi.如果参与者Puj向{Pu1，Pu2，…，Put}广播虚假的信息Qij，则除以外的参与者无法计算出正确的Mi.

2.2.2安全信道问题

原方案的子密钥分配阶段中，D将{aj，bj}，1≤j≤n经过“安全信道”发送给参与者Pj.在开放式网络环境中，真正意义的安全信道是不存在的，建立相对安全的信道代价很大.

2.2.3广播窃听攻击问题

在原方案密钥重建中，Puj广播信息Qij，在没有适当保护措施情况下，攻击者可以通过窃听该信息，并利用公告栏上的公共信息重建Ti，进而计算Mi=Ri-Ti获取共享密钥.

3　对Duoliu方案的改进及安全性分析案例

3.1本文提出的改进方案

针对Duo Liu方案中的分发者/参与者欺诈攻击、广播窃听攻击和安全信道问题，本文基于单向散列函数，密钥协商协议和动态多方Deffie-Hellman提出一种改进方案.

方案分为四个阶段：初始化阶段，子密钥分配阶段，构造阶段、验证重建阶段.具体如下：

3.1.1初始化阶段

D为可信的分发者，{P1，P2，…，Pn}为参与者集合，D通过公告栏发布公开消息.初始化阶段如下：

1）D选定有限域GP（q）上的椭圆曲线E，其中q= pr，p是一个大素数，以使得有限域中椭圆曲线E（GP（q））上的离散对数问题是难解的.随后D选择一个大素数l以及E（GP（qk））上的l-挠群E[l]，其中k是一个整数；

3）D在公告栏中公布{E，q，l，k，α，β，G，H}；

4）D选择一个动态多方Deffie-Hellman协议DH（·），随后{P1，P2，…，Pn}共同协商出一个整数秘密信息，e在l下可逆；

5）D选择一个单向散列函数H（·）∶E[GP（qk）]→{i|1≤i≤l-1}，其输入为有限域上的椭圆曲线E[GP（qk）]上的点，输出为整数

3.1.2子密钥分配阶段

1）D计算一个范得蒙矩阵A：

3.1.3构造阶段

3）D计算并在公告栏上公开

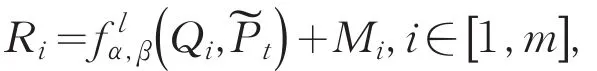
3.1.4验证重建阶段

假设t个参与者{Pu1，Pu2，…，Put}要重建秘密信息，重建步骤如下：

2）计算Puj计算Qij=（Qi，Suj），Vij=eQij，其中Suj=为初始化阶段分发者与所有参与者共同协商的秘密信息.

3）Puj将Vij广播给参与者{Pu1，Pu2，…，Put}{Puj}，

4）Puj收到来自其他参与者的广播信息Vik后，计算，，随后Puj计算

5）Puj从公告栏上下载并比较hik和

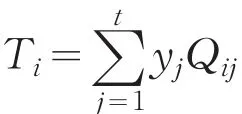
7）Puj计算Mi=Ri+Ti得到秘密Mi.

3.2安全性分析案例

3.2.1分发者/参与者欺诈攻击案例

在子密钥分配阶段，D与参与者Pj通过密钥协商确定子密钥{aj，bj}，故不再需要由D向Pj发送子密钥信息，从而防止了分发者欺诈行为.

在构造阶段，D对所有Pj计算Qij=（Qi，Sj）以及hij=H（Qij），并公布hij.在验证重建阶段，Puj收到来自其他参与者的广播信息Vik后，计算Qik=e-1Vik，随后计算，Puj从公告栏上下载hik并与比较，如果，则拒绝接受Puk发来的信息Vik；如果，则接受该信息.若恶意的参与者Puk向Puj发送虚假的信息Vik，则Puj计算得Qik=e-1Vik必然是错误的，使得，导致Puj拒绝Vik，从而防止了参与者的欺诈行为.而根据单向散列函数的性质，攻击者无法通过hij=H（Qij）获得关于Qij的信息，因此这种验证机制的引入不会影响方案的安全性.

3.2.2安全信道案例

在子密钥分配阶段，D与Pj通过密钥协商确定子密钥，因为密钥协商过程是在公开信道环境中完成的，不依赖于安全信道，因此使方案摆脱了对安全信道的依赖.由此导致子密钥分配阶段流程上的变动，即D不再随机选取2t个数字，而是通过2n个数字{aj，bj}计算得到，不会影响方案的可行性.

3.2.3广播窃听攻击案例

在初始化阶段，D选择一个动态多方Deffie-Hell⁃man协议DH（·），随后与{P1，P2，…，Pn}共同协商出一个整数秘密信息，e可逆；在验证重建阶段，Puj计算Vij=eQij，并将Vij广播给参与者{Pu1，Pu2，…，Put}{Puj}.假设攻击者C成功窃听了所有参与者的广播信息Vij，根据有限域上椭圆曲线离散对数问题的难解性，他也无法在不知道秘密信息e的情况下计算得Qij，并进一步提取得到Mij.

同理C虽然可以利用收集到的Vij信息计算= eTi，但是他也无法在不知道秘密信息e的情况下计算得Ti，并进一步提取得到Mi.从而使方案能够抵御广播窃听攻击.

4　总结

在Liu等人的设计方案的基础上基于单向散列函数、动态多方Deffie-Hellman协议和密钥协商协议提出了一种改进的基于椭圆曲线上自双线性映射的多秘密共享方案.该方案可以抵御分发者/参与者欺诈问题、广播窃听攻击，并摆脱对安全信道的依赖.主要增加计算量来自模指数运算.目前已经存在很多针对模指数运算的快速算法，因此不会给改进方案带来过多的运算负担.本章在保持了原方案优良特性的同时，给出了一种安全性和实用性更好的多秘密共享方案.

[1]Shamir A.How to share a secret[J].Communications of the ACM,1979,24(11):612-613.

[2]Chien H Y,Tseng J K.A practical(t,n)multi-secret sharing scheme[J].IEICE Transactions on Fundamentals of Elec⁃tronics,Communications and Computer,2000,83-A(12): 2762-2765.

[3]He J,Dawson E.Multistage secret sharing based on oneway function[J].Electronics Letters,1994,30(19):1591-1592.

[4]Chor B,Goldwasser S,Micali S,et al.Verifiable Secret Shar⁃ing and Achieving Simultaneity in the Presence of Faults[C]. In:Proc.26th IEEE Symposium on Foundations of Comput⁃er Sciences(FOCS'85).Los Angeles:IEEE Computer Society, 1985:383-395.

[5]Lee H S.A self-pairing map and its applications to cryptogra⁃phy[J].Applied Mathematics and Computation,2004,151: 671-678.

[6]Liu D,Huang D,Luo P,et al.New schemes for sharing points on an elliptic curve[J].Computers and Mathematics with Applications,2008,56:1556-1561.

责任编辑：黄澜

A Multi-secret Sharing Scheme Based on Self-bilinear Pairing Algorithm Elliptic Curves

ZHANG Shangtao
（Department of Computer Engineering Fujian Polytechnic of Information Technology，Fuzhou 350003，China）

Duolius multi-secret sharing scheme based on self-bilinear pairing over elliptic curves is analyzed.Duolius Scheme is found vulnerable to dealer/participant fraud attack,broadcast wiretap attack,and dependent on secure communi⁃cation channel.An improved scheme based on hash function,key agreement protocol,and dynamic multi-party Deffie-Hell⁃man protocol is proposed to eliminate the above deficiencies.Security performance is discussed in the end.

Elliptic curve；self-bilinear pairing；multi-secret sharing；fraud attack；broadcast wiretap attack

TP393.1

A

1674-4942（2016）01-0036-04

2015-10-26