基于Burg entropy-散度函数的不确定概率约束优化问题的等价形式
2016-10-17任咏红赵得利顾钰
任咏红,赵得利,顾钰
(辽宁师范大学数学学院,辽宁大连116029)
基于Burg entropy-散度函数的不确定概率约束优化问题的等价形式
任咏红,赵得利,顾钰
(辽宁师范大学数学学院,辽宁大连116029)
许多有重要价值的实际问题的数学模型均为概率优化模型,如水库系统设计问题、现金匹配问题等,该类模型通常存在分布的不确定性.文章对概率优化模型的分布不确定性展开研究,探讨了基于Burg entropy-散度函数的不确定概率约束优化问题的一个等价形式.构造了基于Burg entropy-散度函数的不确定集,用测度变换的方法把一个关于分布P的优化问题转化为关于似然比的凸优化问题,证明了基于Burg entropy-散度函数的不确定概率约束优化问题解的存在性,并且得到了基于Burg entropy-散度函数的不确定概率约束优化问题的等价形式.
Burg entropy-散度函数;似然比;不确定概率约束优化;测度变换
许多有重要价值的实际问题的数学模型均为如下形式的概率约束优化(CCP)模型:

其中x是d维的决策向量,P表示分布P的不确定集,ξ是Ξ⊂Rk上的服从概率分布P的随机向量,并且X⊂Rd,f∶Rd→R,H(x,ξ)∶Rd×Rk→R是实值函数,Pr~P表示关于分布P的概率,β是预先给定的置信水平.这里的分布P通常存在着不确定性,这就给问题(CCP)的求解增加了很大的难度,因而求解该类问题的关键是构造不确定集.对于不确定集的构造,学者做了大量的研究.如Delage和Ye[1](2010)利用历史数据构造了关于均值向量和协方差矩阵的置信集.Goh和Sim[2](2010)研究了具有方向偏差信息的均值向量的易处理的圆锥表示集等,其中具有代表性的工作是通过恰当的统计得到分布的一个估计P0(称为额定分布).根据概率分布P和额定分布P0的距离不大于一个确定常数来构造不确定集.确定两个分布间的距离有很多方法,如Hu和Hong[3](2013)研究了用KL散度定义概率分布不确定集的分布鲁棒优化问题.任咏红[4]等(2015)讨论了基于修正的χ2-距离散度函数的不确定概率约束优化问题.
本文基于Burgentropy-散度函数确定分布P的不确定集,研究了问题(CCP)的约束条件,应用测度变换的的方法将其转化为关于似然比的凸优化问题,得到基于Burgentropy-散度函数的不确定概率约束优化问题解的存在性,并建立了基于Burgentropy-散度函数的不确定概率并约束优化问题的等价形式.
1 基于Burg entropy-散度函数的不确定集
考虑Burgentropy-散度函数
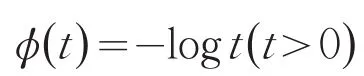
显然,函数在t>0时是凸函数,且满ϕ(1)=0,对a>0有
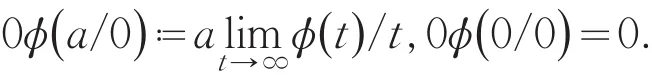
P0是随机变量ξ的额定分布,假设k维分布P和P0在Ξ⊂Rk上存在密度函数分别为p(ξ)和p0(ξ).基于Burgentropy-散度函数,定义分布P到P0的Burgentropy-散度为
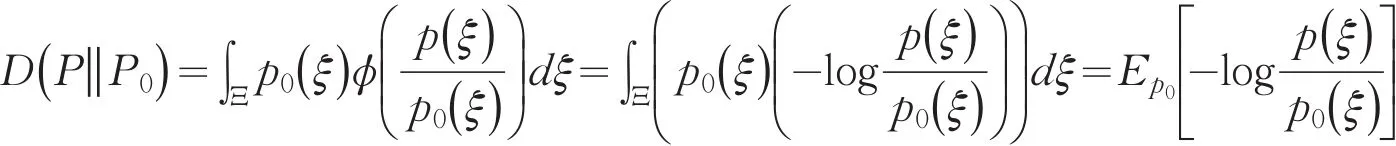
当P0是离散分布时,p0(ξ)表示概率质量函数.当P0是混合分布时,如果P0在ξ处有0质量,那么p0(ξ)表示在ξ处的密度.若P0在ξ处有一正质量,则p0(ξ)表示在ξ处的概率质量函数,显然,并且且仅当在分布P0下几乎处处(a.s.)有p(ξ)=p0(ξ).称为似然比,显然则分布P到分布P0的Burgentropy-散度为
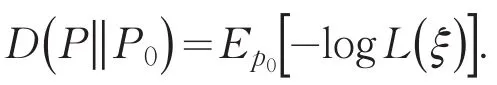
应用Burgentropy-散度构造额定分布P0的一个邻域,得到不确定集

其中D表示所有概率分布的集合,η为任意大于0的数.
2 不确定概率约束的转化形式
考虑概率约束优化(CCP)模型:
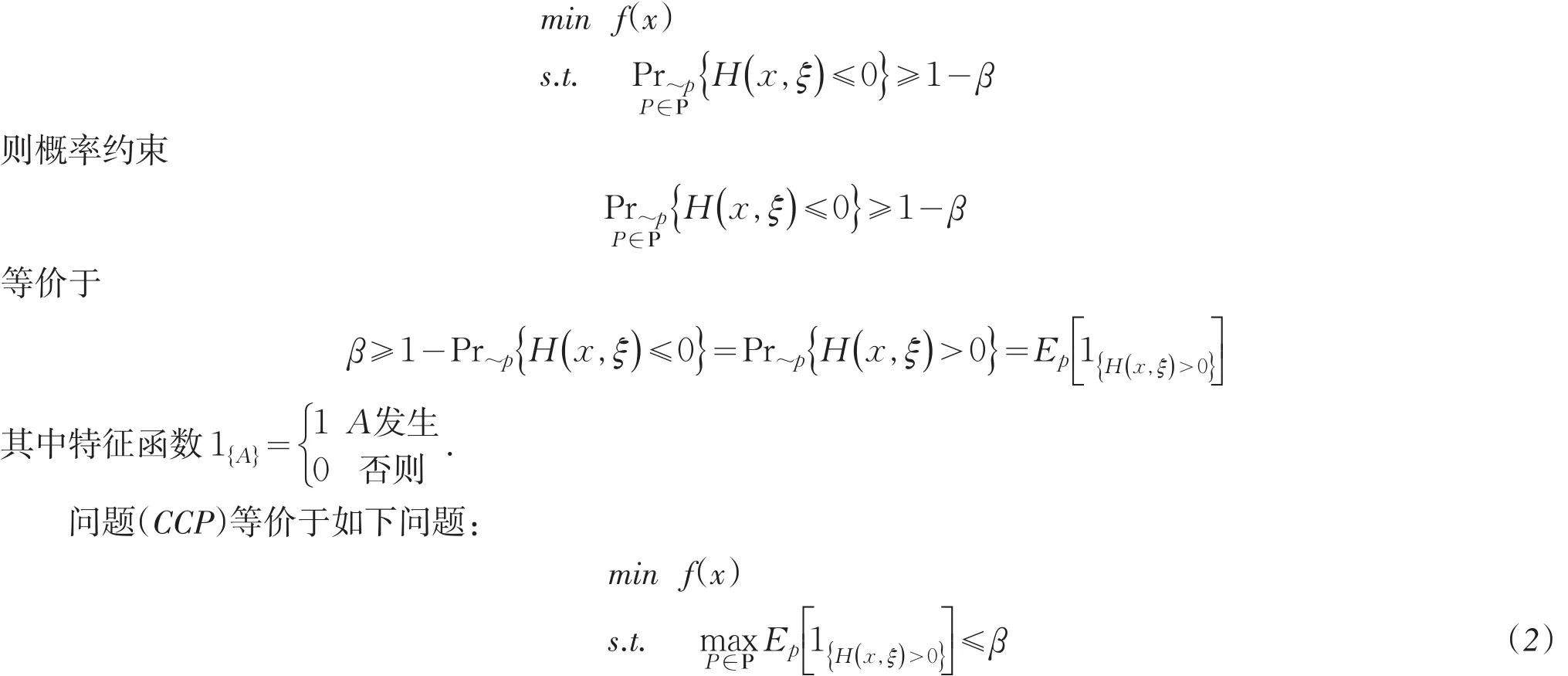
该问题是一个相当抽象的优化模型,因为其中决策变量的概率分布P是不确定的,这使问题很难处理.而解决问题(2)的一个关键步骤是约束函数所对应的优化问题的求解.
考虑问题(2)的约束函数

应用测度变换的方法得到

结合(1)和(4),问题(3)就可以转化为如下形式

命题1:问题(5)是关于L(ξ)的凸优化问题.
证明令
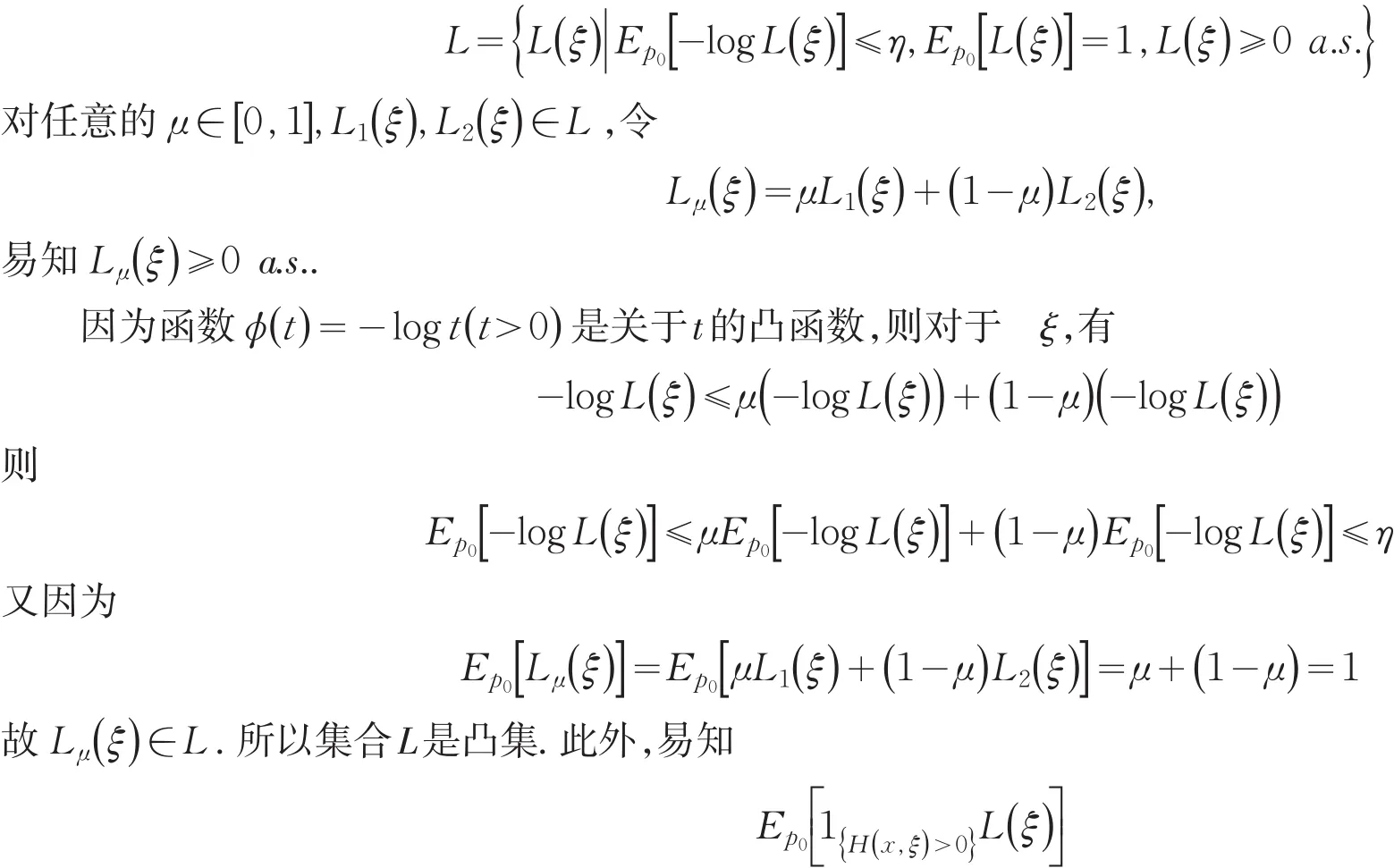
关于L(ξ)是凹的.因此问题(5)是凸优化问题,命题得证.
问题(5)的Lagrange函数为
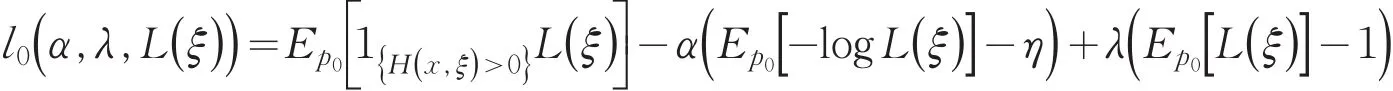
则问题(5)等价于

问题(6)的对偶问题为

可以证明问题(6)和问题(7)之间的强对偶定理成立.从而要想求解问题(5),只需求解问题(7)即可.
3 内部极大化问题的求解
问题(7)的内部极大问题的求解可以转化为求解如下问题

设v(λ,α)是问题(8)的最优值函数,考虑如下两种情况:
(1)当α=0时,设Hμ(x)是在分布P0下的本质上确界,即
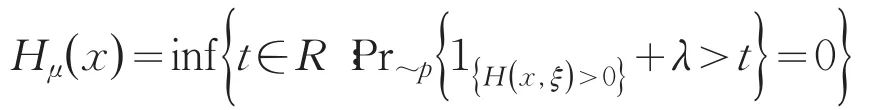
构造一个分布序列Pj< 因此,v(λ,α)=Hμ(x). (2)当α≠0时,定义函数 易证J(L(ξ))关于L(ξ)是凹的,那么就有J(L(ξ))的方向导数存在,记DJ(L(ξ))表示J(L(ξ))的方向导数,则对于在L(ξ)处的任意可行方向V(ξ): 因为当t∈R+时,函数ϕ(t)是凸函数.所以对任意的L(ξ)和可行方向V(ξ),函数 关于t是单调递增的,因此由单调收敛定理可知 由命题1可知,问题(8)是一个无约束的凸优化问题,因此问题(8)的最优解即为Lagrange函数l0(α,λ,L(ξ))的稳定点,即l0(α,λ,L(ξ))的导数为0时方程的解. 定理得证. 由定理得,基于Burgentropy散度函数,问题(7)等价于 [1]Delage E,Ye Y.Distributionally robust optimization under moment uncertainty with application to data-driven problems[J].Op⁃erations Research,2010,58:595-612. [2]Goh J,Sim M.Distributionally robust optimization and its tractable approximations[J].Operations Research,2010,58(4):902-917. [3]Hu Z,Hong L J.Kullback-Leibler divergence constrained distributionally robust optimization.Technical report[EB/OL].http:// www.optimization-online.org/DB_FILE/2012/11/3677.pdf. [4]任咏红,王榆,赵得利.基于修正的x2-距离散度的不确定概率优化问题[J].辽宁师范大学学报:自然科学版,2015,38(2):156-160. 责任编辑:刘红 An Equivalent Form of Ambiguous Probabilistic Constrained Optimization Problem Based on Burg Entropy-divergence Function REN Yonghong,ZHAO Deli,GU Yu Many practical problems with important values can be modeled as probabilistic optimization problems,such as reservoir system design,cash matching,and so on,in which often exists distribution of uncertainty.This paper facuses on the uncertainty distribution,and aims at studying an equivalent form of ambiguous probabilistic constrained optimization prob⁃lem based on Burg entropy-divergence function.Ambiguous set based on Burg entropy-divergence is constructed.With the change-of-measure technique,the optimization problem with respect to distribution P is converted to a convex optimization with respect to likelihood ratio.Existence of solutions of ambiguous probabilistic constrained optimization problem is proved based on Burg entropy-divergence function.Consequently,we obtain the equivalent form of ambiguous probabilistic con⁃strained optimization problem based on Burgentropy-divergence function. Burg entropy-divergence;likelihood ratio;ambiguous probabilistic constrained optimization;change-of-mea⁃sure technique O 221.5 A 1674-4942(2016)01-0001-05 2015-09-13 国家自然科学基金面上项目(11171138);辽宁省教育厅科学研究一般项目(L2015291)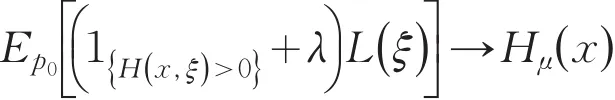
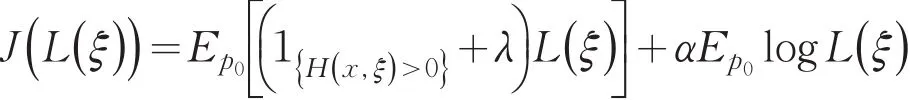
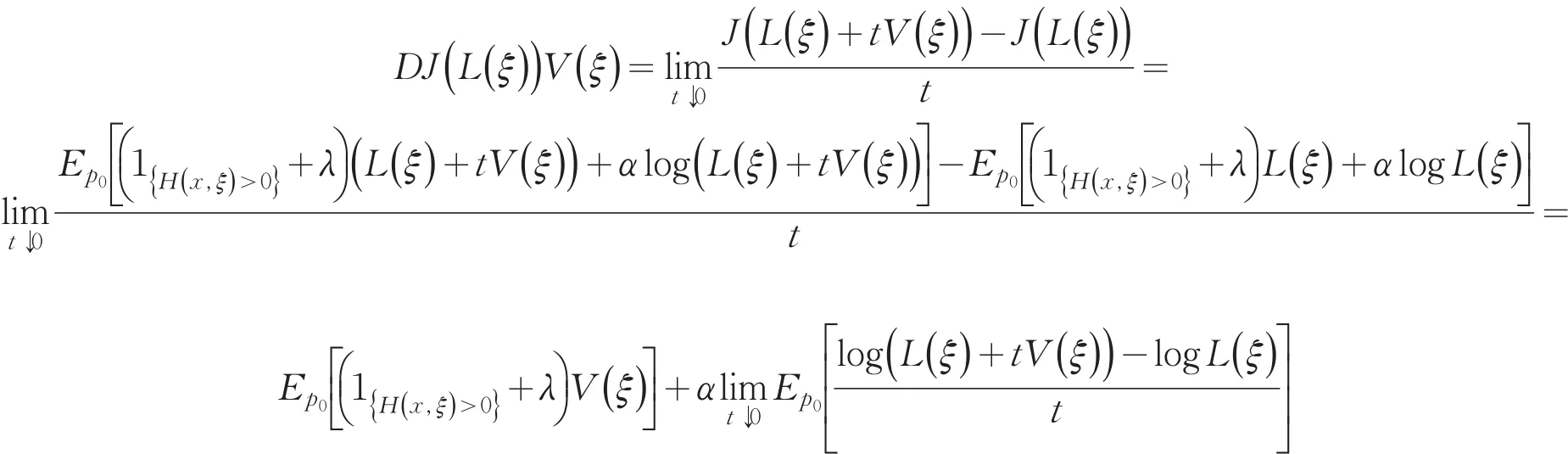

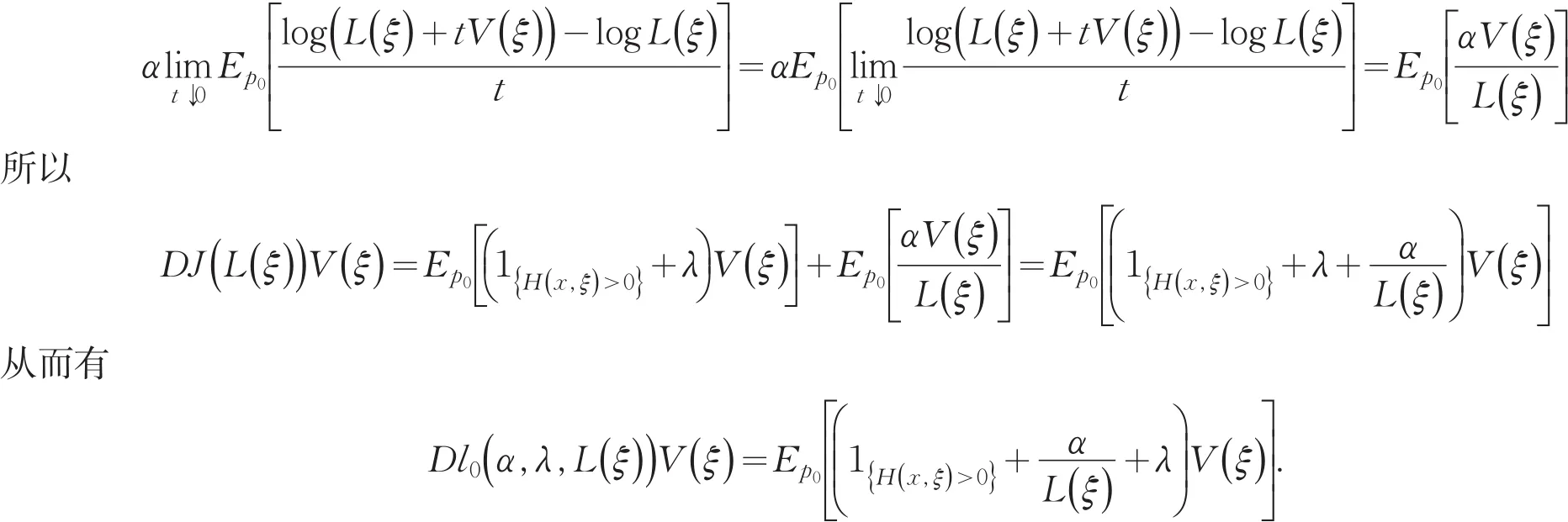
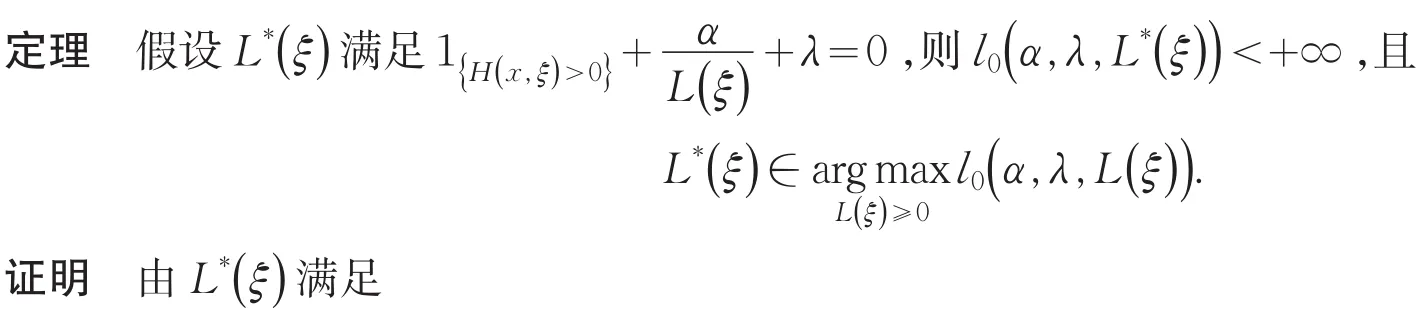
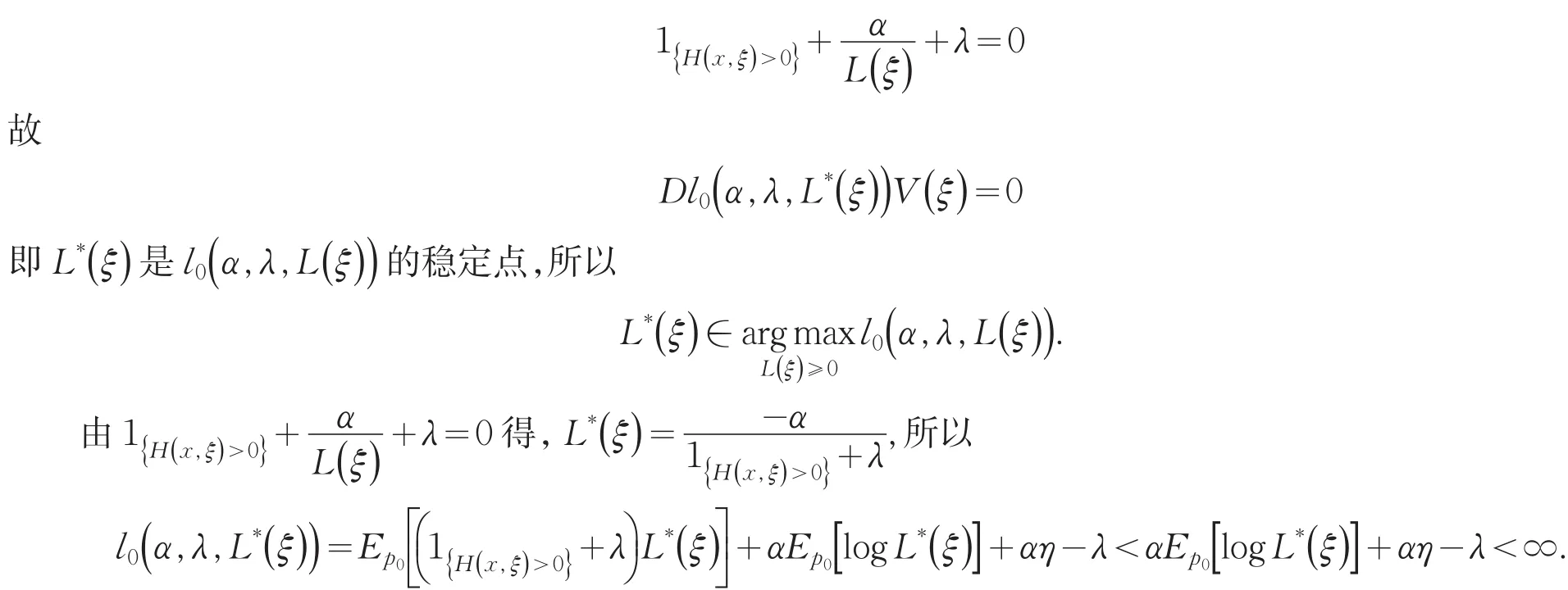
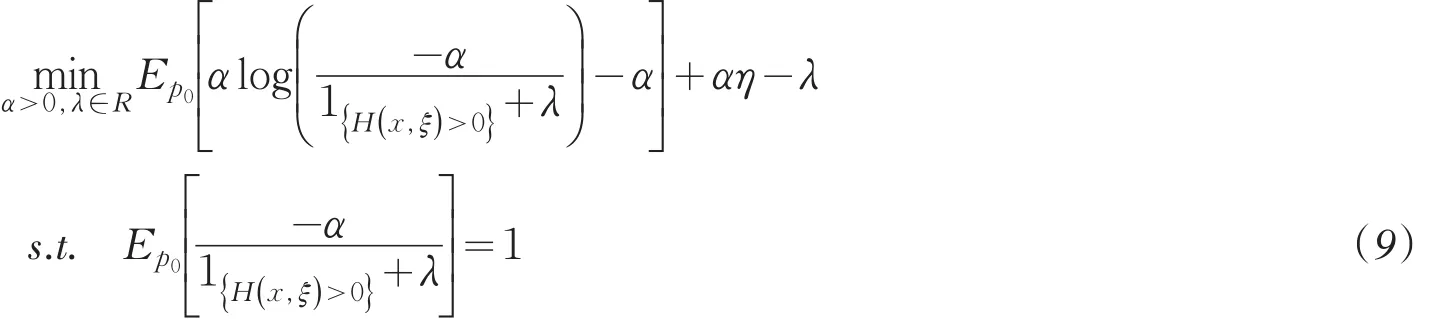
(School of Mathematics,Liaoning Normal University,Dalian 116029,China)
