基于改进型经验法则的工艺偏差统计

李霓，齐琦，王凯华*

（1.海南师范大学数学与统计学院，海南海口571158；2.海南大学信息科学技术学院，海南海口570228）

基于改进型经验法则的工艺偏差统计

李霓1，齐琦2，王凯华1*

（1.海南师范大学数学与统计学院，海南海口571158；2.海南大学信息科学技术学院，海南海口570228）

文章在改进经验法则的基础上，对工艺参数的偏差进行了统计分析.首先由切比雪夫不等式引入基于正态分布的经验法则，然后利用后验概率密度最大值点替代经验法则式中的均值点，对经验法则进行了改进，并应用改进型经验法则寻找实际工艺参数数据的局部偏差，进而对工艺参数进行趋势分析，得到了工艺参数偏离趋势的判定结果.该方法比经验法则更有效，可推广到某些特定的与均值有关的分布法则中去，用于分析工业生产领域中有偏离群的数据，具有一定的普适性和应用价值.

切比雪夫不等式；经验法则；后验概率密度；工艺偏差

工艺参数是指在工艺流程中影响生产过程的关键变量，是工艺条件的量化指标.常见的工艺参数有温度、压力、水碳比和物料比等.由于设备、工艺条件、环境、物料构成等因素的限制，或者生产流程中没有正常地履行操作规程的要求，时常存在工艺指标发生偏离的情况.在该种情况下，工艺参数并非精确地符合额定值，而是与额定值之间存在着一定的偏差，这种差异即定义为工艺偏差.工艺偏差的产生往往不是偶然的，而是预示着生产流程中出现了某种失误，严重到一定程度甚至会发生重大安全事故，所以应根据具体的生产条件和工艺偏差的特点，定期查找导致工艺偏差的成因，并采取适当措施以防止工艺偏差对工业生产造成的不利影响.为了能够加强工艺指标的监控，必须将工艺指标偏离的情况标注出来，从而可以采取一定的手段对该偏离进行重点监控.除了工艺参数的局部偏离以外，还可能存在工艺参数缓慢地向上或者向下偏离的趋势，并且这种趋势长期存在，在短期内很难迅速察觉.在生产过程中，对工艺参数大多进行了自动控制，通常在设定点附近保持微小的振荡，但是受多种因素影响还是会有长期偏离的情况发生.这种工艺参数缓慢演变的长期趋势对于生产过程所产生的不利影响可能是相当严重的，为了保持平稳运行和生产成本，必须及早发现并避免这种情况的发生.因此，通过算法寻找出工艺参数偏离的长期趋势，对于维护工艺流程的稳定性和可控性具有很强的指导意义.

1　改进型经验法则

1.1经验法则

对于一个随机分布的变量而言，方差作为其离散程度的度量，反映了该随机变量离开数学期望的平均偏离程度.如果随机变量记为ξ，方差为Dξ，那么对任意大于零的常数ε，随机变量偏离期望不小于ε的概率满足著名的切比雪夫不等式[1].

定理（切比雪夫不等式）对任意的随机变量ξ，若Eξ=μ，且Dξ存在，则对∀ε>0，有

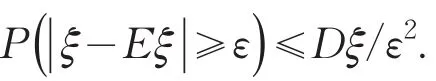
在切比雪夫不等式中，只需要知道分布的期望和方差这两个数字特征，因此使用起来比较方便，但由于没有充分利用随机分布的密度函数等信息，导致它给出的估计比较粗糙.为了给出更加精细的结果，通常对待研究的变量施以某种分布假定，在此基础上再进行推断.不妨假定研究变量服从正态分布N（μ，σ2），则有

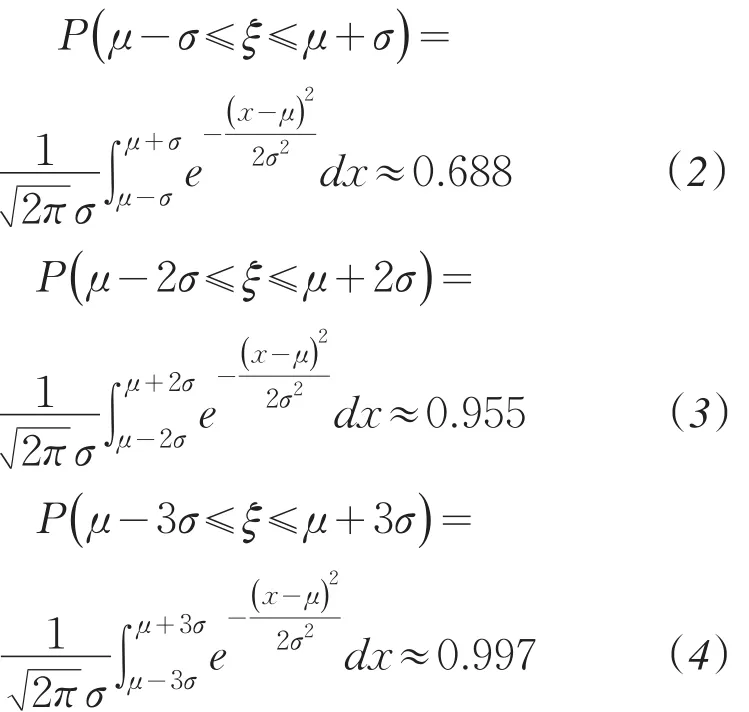
上式表明，正态分布的随机变量偏离其期望不超过σ的概率略大于，不超过2σ的概率在0.95以上，而超过3σ的概率则只约0.003，即在实际问题通常认为是不会发生的.也就是说，对服从N（μ，σ2）的随机变量而言，基本上可以认为有，该式通常被称为经验法则.

若使用切比雪夫不等式，则可得

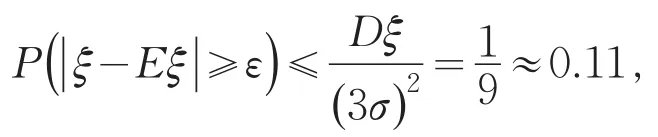
不如经验法则的结果精细，因此在实际工作中，经验法则往往比切比雪夫不等式更加常用.

1.2工艺偏差统计模型

由于位号的实际观测值可以看成是工艺参数的设计值加上随机扰动项，因此对于工艺偏差有如下的统计模型：

其中，Xt为位号观测值，μ为工艺参数设计值.从以上模型可以看出，工艺偏差εt的统计可以通过统计Xt来实现.对工艺参数历史数据初步核算后发现，大部分工艺位号具有正态的随机扰动，因此可以对Xt应用经验法则.另外，由于工艺参数的均值受少数异常值如停车数据的扰动极大，可将μ用众数[2]（后验概率密度最大值点）而非均值来估计.

1.3趋势估计模型

工艺参数除了具有局部偏差，从长期来看，还会具有向上偏离或者向下偏离的趋势.对于工艺参数的长期趋势，可以用如下的统计模型来刻画：

对此模型在相当长的一段时间内进行拟合，如果斜率β1>0，则认为工艺参数具有向上偏离的趋势；若β1<0，则认为工艺参数具有向下偏离的趋势；若β1=0，则认为工艺参数在该时期内不具有偏离趋势.该模型不应该建立在过于短的时期内，因为在很短的时间内，工艺参数观测值时而上升时而降低是很正常的，实时计算并判断β1的符号会显得过于频繁而且没有意义.

2　基于改进型经验法则的工艺偏差统计

在收集到工艺参数的时间序列数据后，直接对原始数据进行趋势项的拟合，发现异常值对拟合结果的干扰较大，严重影响了对整体趋势的正确判断.比如通过对工艺参数位号AMM2.VI2500.PV的分析[3]发现存在显著向上的偏离趋势，但是在排除最后5日的观测值之后再重新分析，向上偏离的趋势变得不再显著（见图1），即认为总体不存在偏离趋势.同理，对工艺参数位号AMM2.TI2504.PV和AMM2. FN1001.PV的总体趋势的判断也受到了停车阶段（2012年3月31日0：00至2012年5月7日0：00，对应图1中横坐标60—97）和异常波动期（2012年7月5日0：00至2012年7月18日，对应图1中横坐标156—169）这两段下凹数据的干扰.因此要先剔除工艺参数数据中存在的异常值，再进行整体趋势的拟合.

工艺参数的后验概率密度在众数处达到最大，故以其为中点，上下各扩展一定的百分比（不妨取为40%）作为正常值范围的上下限，从而允许一定的相对误差.由于工艺参数均值受到了较多来自停车阶段和异常波动阶段的异常值干扰，因此不再适合作为工艺参数正常值的参照标准.假定现实生产过程中工艺参数的取值在绝大部分时段都属正常，众数作为后验分布中具有明显集中趋势点的数值，代表了数据点出现频率最高的值，将其作为正常值范围的中心是合理的[4-7].接下来，计算所有介于当前上下限之间的工艺参数的均值和标准差，并根据经验法则来界定新的上下限，从而得到了排除局部偏差的工艺参数正常值范围.基于最小二乘法的线性回归分析方法[8-9]，对该范围之内的工艺参数时间序列作趋势分析，并根据时间项系数估计的显著性和正负性来判断工艺参数过程有无整体趋势以及趋势的方向：若斜率项P值小于预先指定的显著性水平，则认为有整体偏离趋势，反之，则认为整体趋势平稳；若斜率项估计为正，则有整体上升趋势，若斜率项估计为负，则有整体下降趋势.

图1　异常值干扰趋势分析结果Fig.1The results of outliers disturb trend analysis

3　结论

采用基于改进型经验法则的工艺偏差统计方法，对中海石油化学股份有限公司于2012年1月1日0：00至12月31日23：59期间采集到的500个典型工艺参数的8784个整点数据进行偏差和趋势分析，在显著性水平0.05下，筛选出了85个具有向上偏离趋势的工艺参数，以及43个具有向下偏离趋势的工艺参数.最具有代表性的工艺参数偏离趋势如图2-5所示.这些结果的获取，对于工业生产过程的质量控制和管理具有极大的指导意义.事实上，在工艺偏差统计结果的指导下，通过采取相应的措施，2013-2015年的非计划停车次数从以往年份的1-2次降到了0次.在对工艺偏差进行统计分析的过程中，我们选取众数而非均值作为工艺参数的正常值，有效避免了异常值对工艺参数统计的干扰.在相对百分数误差限的基础上，应用经验法则进一步改良了上下限.在整体趋势分析中，我们应用了时间序列分析中对时间趋势进行拟合的常规方法，对工艺参数依不同的时间间隔进行聚合处理，并据此计算平均显著性，从而避免了时间跨度过大、数据集过于稠密对趋势项显著性的影响，得到了更有信度的结论.

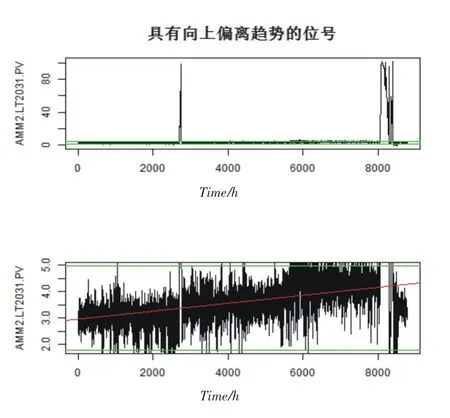
图2　具有向上偏离趋势的工艺参数AMM2.LT2031.PV(液位位号)Fig.2The process parameter of AMM2.LT2031.PV with a trend of going up

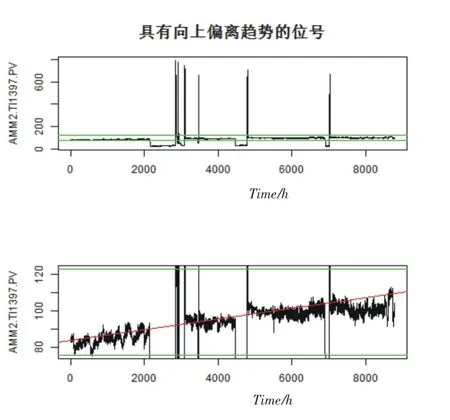
图3　具有向上偏离趋势的工艺参数AMM2.TI1397.PV（温度位号）Fig.3The process parameter of AMM2.TI1397.PV with a trend of going up

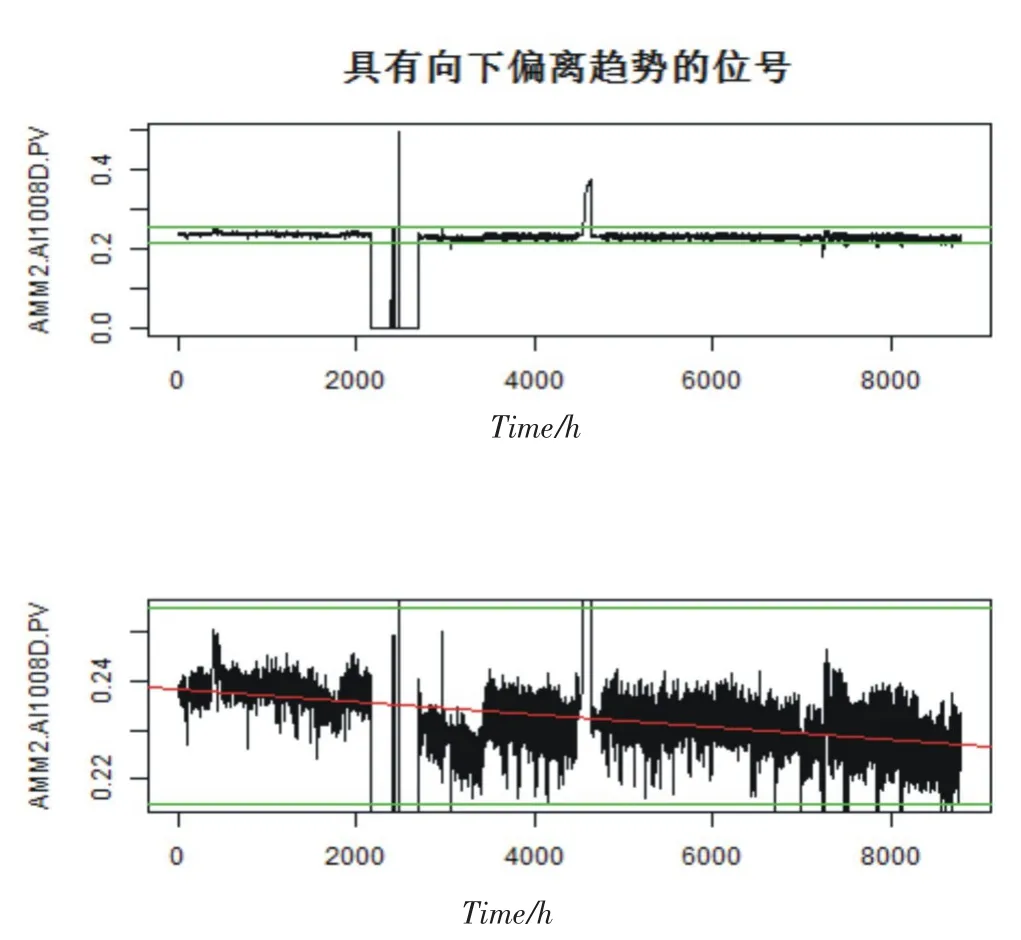
图4　具有向下偏离趋势的工艺参数AMM2.AI1008D.PV（天然气组分位号）Fig.4The process parameter of AMM2.AI1008D.PV with a trend of going down

图5　具有向下偏离趋势的工艺参数AMM2.LT2012A.PV（液位位号）Fig.5The process parameter of AMM2.LT2012A.PV with a trend of going down

[1]茆诗松,程依明,濮晓龙.概率论与数理统计（第二版）[M].北京:高等教育出版社,2011.

[2]Basu S,Anirban D.The mean,median,and mode of uni⁃modal distributions:a characterization[J].Theory of Proba⁃bility and Its Applications,1997,41(2):210-223.

[3]Becker R A,ChambersJ M，Wilks A R.The New S Lan⁃guage[M].Wadsworth&Brooks/Cole,1988.

[4]Scott D W.Multivariate Density Estimation.Theory,Prac⁃tice and Visualization[M].New York:Wiley,1992.

[5]Sheather S J,Jones M C.A reliable data-based bandwidth se⁃lection method for kernel density estimation[J].J Roy Stat⁃ist Soc B,1991,53(3):683-690.

[6]Silverman B W.Density Estimation[M].London:Chapman and Hall,1986.

[7]Venables W N,Ripley B D.Modern Applied Statistics withS[M].New York:Springer,2002.

[8]Chambers J M.Linear models.Chapter 4 of Statistical Mod⁃els in S eds J.M.Chambers and T.J.Hastie[M].Wadsworth &Brooks/Cole,1992.

[9]Wilkinson G N,Rogers C E.Symbolic descriptions of facto⁃rial models for analysis of variance[J].Applied Statistics, 1973,22(3):392-399.

责任编辑：刘红

Deviation Analysis of Process Parameter Based on Improved Empirical Rule

LI Ni1，QI Qi2，WANG Kaihua1*
（1.School of Mathematics and Statistics，Hainan Normal，Haikou 571158，China；2.School of Information Science and Technology，Hainan University，Haikou 570228，China）

Empirical rule is frequently used for analyzing variables which follow a normal distribution.It can be improved via replacing the empirical mean by the mode and the value which maximizes the empirical density function of the continu⁃ous variable.This improved empirical rule can then be applied to analyze adataset of process parameter and the results illus⁃trate that it works well.Furthermore,the improved empirical rule can also be generalized to more circumstances where mean-related distribution rules apply.

Chebyshev inequality；empirical rule；posteriori probability density；deviation

O 212.2

A

1674-4942（2016）01-0022-04

2015-11-21

国家自然科学基金项目（11401146，11361022）；海南省自然科学基金项目（20151006，20151010，20156243）；海南省高等学校教育教学改革研究项目（HNJG2014-22）