砂土注浆颗粒流数值模拟研究

秦鹏飞

(郑州工业应用技术学院 建筑工程学院，河南 郑州 450010)



砂土注浆颗粒流数值模拟研究

秦鹏飞

(郑州工业应用技术学院 建筑工程学院，河南 郑州 450010)

基于流固耦合原理的PFC2D颗粒流数值模拟程序，运用其内置FISHTANK函数库和FISH语言，分别定义流体域的流动方程和压力方程，对灌浆过程中浆液在地层中的扩散过程和形态进行了数值模拟计算.通过调节PFC命令流中的注浆压力p、时步step、水力传导系数perm等参数对浆液的注浆过程进行了模拟计算.数值模拟计算表明，灌浆过程中浆液与地基土的作用形式与灌浆压力大小密切相关，过高的注浆压力会对地层结构造成一定的破坏.对钻孔周围土体的应力状态进行了理论推导和分析，理论推导结果与数值模拟结果相符.劈裂灌浆作用发生时，孔隙率和应变率均增加.而浆液的渗透性能对高压劈裂灌浆的作用效果影响不明显.

砂砾石土；注浆；颗粒流；数值模拟；渗透性质

自十九世纪初以来，灌浆技术以其设备简单、施工灵活、适应地基变形能力好等特点得到了广泛应用[1].浆液灌入到地层后，通过渗透、压密和劈裂等方式与土体相互作用，以改善砂砾石土体的性能，其作用机理非常复杂.由于浆液在地层中的扩散过程和形态是隐藏的，浆液与土体间的渗透、压密或劈裂等作用方式的发生发展进程无法直接观测，使得灌浆理论的研究远落后于工程实践的需要[2].

在数字信息技术高速发展的背景下，作为对土工现场或室内试验技术的一种补充，深入开展土工试验的数值仿真研究具有重要的意义和价值[3].现场或室内物理试验往往存在试验周期长、费用高等不利因素的影响，而对注浆过程进行细观力学数值模拟分析研究，可以克服这些缺点[4].数值分析法能够保证地层结构的完全“同一性”，任意时刻地层内部应力场及应变等物理力学参数的分布状态与统计信息也可以准确完整地反映出来，因此数值仿真模拟研究已成为注浆工程中令人瞩目的研究方法，并得到了广泛的关注和应用[5].

周健[6-7]基于颗粒流理论，运用PFC2D计算程序的FISHTANK函数库和FISH语言，对砂土的工程力学性质和土中的渗流过程进行了模拟；吴顺川[8]采用岩土颗粒流程序，从微观上模拟了单孔和多孔条件下不同注浆压力对土体改性效果的影响，模拟结果与现场注浆试验取得了较为一致的结果；孙锋[9]对致密土体的劈裂注浆过程进行细观模拟研究，分别对比了不同注浆压力和不同土体性质下浆体压力扩散及劈裂缝的发生、发展规律；袁敬强[10]基于散体介质理论的颗粒流方法，运用 PFC2D软件对软弱地层注浆过程进行了细观力学模拟，研究了注浆压力、注浆时间、渗透性质及颗粒黏结强度对浆液扩散半径和注浆类型的影响规律.

从已有的成果看，针对砂砾石土层灌浆浆液扩散机理方面的研究工作相对偏少，同时考虑注浆时间、土层渗透性质等细观参数变化对土体灌浆效果影响的研究也不多见.本文基于流固耦合的原理，采用Itasca公司开发的PFC2D颗粒流数值模拟程序，从细观层面模拟研究了浆液在地层中的扩散和分布形态，并对不同渗透性质土体、不同注浆时间下的灌浆效果进行了初步探索.

1　注浆细观模拟的基本理论

二维颗粒流(PFC2D)程序通过离散单元法来模拟圆形颗粒介质的运动及其相互作用，其解决问题的基本思路是将实际土工问题的物理模型进行抽象和简化，从细观角度建立符合工程特点的数学模型，并对模型赋予一定的物理力学参数和初始条件、边界条件，从而实现对工程问题的仿真求解.颗粒流方法在计算循环中，交替应用牛顿第二定律与力-位移定律，将牛顿第二定律重复应用于颗粒上，力-位移定律重复应用于接触上，并且不断更新颗粒或墙体的位置[11-12].颗粒与颗粒间的接触或颗粒与墙体之间的接触，在计算过程中自动形成或破坏.

1.1流体流动基本方程

PFC2D程序采用颗粒集合模拟岩土体，但并没有实际的流体存在.在PFC2D数值模型中，假想颗粒接触处存在一个相切于两个颗粒的管道(pipe)，作为流体流动的通道；而颗粒间的孔隙形成一个贮存流体的流体域(domain)，相当于一个“水库”承受水压，并与管道连通.储存于其中的流体压力在灌浆模拟过程中不断更新，以实现流体与固体之间的相互耦合作用[13].每个管道都是一个潜在的裂隙，相当于长度为L、厚度为a，单位宽度的平板通道.若浆液在管道内的流速恒定，流体介质内部分子在流动过程中无杂乱，基本呈层流状态，则其流动规律遵从平板缝隙立方定理，浆液的流量为

(1)

式中k为缝隙内的水力传导系数；a为缝隙高度；L为缝隙长度；p2-p1为两相邻流域的压力差，为正值使域2的流体流入域1.

1.2求解方法

若模型的某一流体域内存在扰动压力△Pp，根据PFC2D计算原理，由于压力扰动而流入该域的流量可计算得出

(2)

式中N为连接到单个域的管道的数量；R为该流体域周围颗粒的平均半径.而这些浆液流入后又会引起该流体域内压力的增加，由式(2)可计算得出

(3)

系统为了保持自身的稳定状态，要求由浆液流入引起的压力变化必须小于扰动压力，即ΔPr<ΔPp.若令浆液流入引起的压力变化等于扰动压力，即ΔPr=ΔPp，则据此可以求出系统保持稳定的时间步长

(4)

2　二维颗粒流数值模拟计算

2.1计算模型

PFC2D颗粒流程序允许生成的颗粒服从均匀分布和Gauss分布，本模拟试验采用的颗粒粒径服从的是均匀分布.颗粒单元的最小半径Rmin=3.5 cm，最大半径Rmax=5 cm.PFC2D模型中的颗粒均生成在坐标值指定的区域内，并且自动为每个生成的颗粒设置ID号.通过输入print ball命令，可以自动查询到所生成颗粒单元的数目、半径、坐标值等信息.本次数值试验共生成1 226个颗粒单元，请见图1(a)所示.在颗粒生成过程中，为了防止由于颗粒粘结强度不足而出现四处逃逸的情况，PFC2D程序允许在生成颗粒前先生成四面墙体( wall)，等颗粒间的不平衡力通过循环消除后，再将墙去掉[14-18].

本计算模型的长和宽各为4 m，内部充填密实的圆盘颗粒以模拟实际的地层结构，如图1(a)所示.模型的边界由一圈红色颗粒围成，代表不透水边界.图1(b)中浅紫色的圆点代表流体域(domain)，由域间的紫色线段构成颗粒间的缝隙通道.模型中浅绿色的圆盘代表地层结构中的土体颗粒，连接圆颗粒间的黑色线段则代表颗粒间的接触连接.

在本次模拟计算前，通过开展双轴压缩试验对砂砾石土的法向接触刚度kn、切向接触刚度ks和摩擦系数fc等细观参数进行了测试，并开展Darcy渗流试验测试了砂砾石土的孔隙率n.结合文献[8-10]、[14]的参数选取情况，本计算模型所取的细观参数如表1所示.

表1　颗粒细观参数

2.2计算方案

本次PFC2D颗粒流数值计算，共设计了2种模拟方案：(1)保持土体模型和细观参数不变，对注浆压力进行调节，研究不同注浆压力对注浆效果的影响；(2)不同注浆时间、不同渗透性质浆液在特定注浆压力下的注浆效果.

(a)土体颗粒流模拟图

(b)流体域与颗粒单元关系图1　二维颗粒流计算模型

3　灌浆压力对灌浆效果的影响

图2给出了压力p=1 MPa作用下土体内部的应力场及浆液的扩散范围分布情况.数值模拟计算中注浆点的位置位于模型的正中心.图中的棕色圆球代表着注浆压力的分布，而圆半径的大小则代表着注浆压力的大小.在图2(a)的应力场中，黑色线条代表压应力，青色线条代表拉应力.可以看出，在注浆压力的作用下，土体内部颗粒互相挤压并向外膨胀，模型的外围出现了较大的压应力，而在注浆孔环向附近则出现了张拉应力.钻孔附近有大量浆液聚集，对土体形成压密作用，而钻孔外围浆液则主要是渗透和充填作用.图2(b)中设置了一系列测量圆对浆液的扩散范围进行了监测，从图2可以看出，浆液的扩散范围大约达到100 cm(每个测量圈各间隔20 cm).

(a)土体应力场

(b)浆液扩散范围分布图2　p=1 MPa压力下土体应力场及浆液扩散范围

图3为压力p=2 MPa作用下土体内部的应力场及浆液的扩散范围分布情况.从图3可以看出，2 MPa的注浆压力已将地层启劈，地层内出现劈裂缝(红色线条代表劈裂缝).由于土颗粒粒径大小不均匀，土体内部应力场较杂乱，劈裂缝基本沿应力薄弱面产生(对应于模型上部和下部土体).模型左侧和右侧部分土体所处应力状态较高，几乎未被注浆压力劈开，仍然表现为渗透注浆形式.图3(b)显示，劈裂缝在各方向上的扩展长度不等，大体分布在40～80 cm之间.

图4为压力p=3 MPa作用下土体内部的应力场及浆液的扩散范围分布情况.可以看出，随着注浆压力的增加，土体内部劈裂的范围不断扩大.劈裂缝的扩展形态更加全面完善，在土体内部形成了纵横交错的网状浆脉，土体劈裂灌浆达到最为理想的效果.但劈裂灌浆过程中不宜过度地提高注浆压力，注浆压力太高易产生地层结构的严重破坏，甚至会出现冒浆、地面隆起等现象.本计算模型中钻孔附近的土体受3 MPa高注浆压力的作用产生了一定的位移，对土体的原状结构造成了一定的破坏.

4　细观注浆结果分析

4.1 孔隙率变化

图5(a)、(b)为注浆压力1 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内土体孔隙率的变化趋势线.与注浆前砂砾石土的孔隙率相比，注浆压力作用下砂砾石土体孔隙率增加约1.2 %～1.7 %.这是由于1 MPa的注浆压力对砂砾石土体具有一定的压密作用，砂砾石土颗粒向外移动孔隙率增加，浆液充填了这部分孔隙.不同的监测范围内砂砾石土孔隙率的变化趋势基本一致，浆液的渗透扩散过程比较平稳.

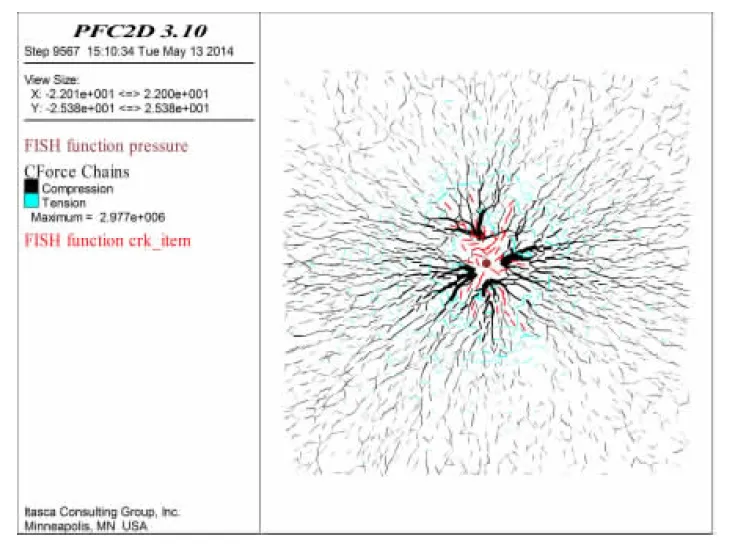
(a)土体应力场

(b)浆液扩散范围分布图3　 p=2 MPa压力下土体应力场及浆液扩散范围

(a)土体应力场(b)浆液扩散范围分布图4　p=3 MPa压力下土体应力场及浆液扩散范围

图5(c)、(d)为注浆压力2 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内土体孔隙率的变化趋势线.可以看出，注浆压力作用下砂砾石土体孔隙率整体也有所增加，增加幅度约为1.18 %～3.78 %.这是由于劈裂缝产生扩大了砂砾石土空间，浆液充填了这部分空间结构.不同的监测范围内砂砾石土孔隙率的变化趋势也基本一致，劈裂缝的扩展过程也比较平稳.

图5(e)、(f)为注浆压力3 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内土体孔隙率的变化趋势线.可以看出，3 MPa注浆压力作用下砂砾石土体孔隙率大幅增加，增加幅度约为23.5 %～33.3 %.这是由于劈裂作用过程更加全面深入，劈裂缝形态更加密集，进一步扩大了砂砾石土空间.

(a) step=1 000 (b) step=2 000

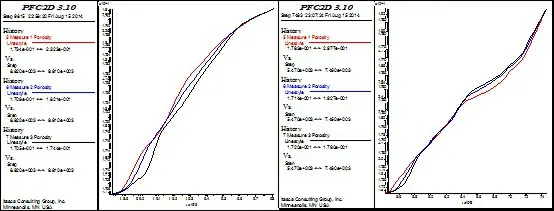
(c) step=1 000 (d) step=2 000

(e)step=1 000(f) step=2 000

图5砂砾石土内部孔隙率变化

4.2 应力变化

图6(a)、(b)为注浆压力1 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内砂砾石土颗粒间x向应力的变化趋势线.可以看出，离注浆孔越近则注浆过程中土体颗粒间的最终应力越大.半径0.5 m监测范围内，x方向最大应力约为9.916×104Pa；半径1 m监测范围内，x方向最大应力约为5.308×104Pa；而半径为1.5 m时，x方向最大应力约3.052×104Pa.

图6(c)、(d)为注浆压力2 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内砂砾石土颗粒间x向应力的变化趋势线.土颗粒间x向应力的变化规律与上图基本相同，0.5 m监测范围最大应力约为3.709×104Pa，1.5 m监测范围最大应力约为1.172×104Pa.

(a) step=1 000(b) step=2 000

(c) step=1 000(d) step=2 000

(e)step=1 500(f) step=2 000

图6砂砾石土内部x向应力变化

图6(e)、(f)为注浆压力3 MPa作用下，监测半径分别为0.5 m、1 m和1.5 m范围内砂砾石土颗粒间x向应力的变化趋势线.砂土颗粒间最大应力约为5.5×105～8.5×105Pa，外侧土颗粒应力变化较内侧有一定规律性延迟.

5　结论

对灌浆过程中浆液在地层中的扩散过程和形态进行了数值模拟计算，通过调节注浆压力、时步、水力传导系数等参数从细观角度对注浆效果进行了分析，所得主要结论如下：

(1)灌浆过程中浆液与地基土的作用形式与灌浆压力大小密切相关.为达到理想的劈裂灌浆效果需要适当提高注浆压力，但过高的注浆压力会对地层结构造成一定的破坏.

(2)对钻孔周围土体的应力状态进行了理论推导和分析，指出土体环向拉应力的增加导致钻孔周围产生劈裂缝，浆液由渗透作用方式向劈裂作用方式转变.理论推导结果与数值模拟结果相符.

(3)劈裂灌浆作用发生时，注浆压力拓展了砂砾石土空间，孔隙率增加.劈裂灌浆对砂砾石土结构具有一定破坏作用，应变率也有较大增加.

(4)流动性能差的稠浆适于压密灌浆和劈裂灌浆，流动性能好的稀浆则适于渗透性灌浆.而高压劈裂灌浆时，浆液的渗透性能对灌浆效果的影响不明显.

(5)基于流固耦合的PFC2D颗粒流程序对于模拟砂砾石等土体的注浆施工提供了一条崭新的思路，但由于土体内部结构的复杂性和现场施工多种不确定性因素的影响，使本文的数值计算与实际情况有一定差异，尚需进一步深入研究.

[1]Duan Hongfei,Jiang Zhenquan, Zhu Shuyun.New composite grouting materials: Modified urea-formaldehyde resin with cement[J].International Journal of Mining Science and Technology,2012(22):195-200.

[2]G.S. Zhao, G.Q. Zhou, G.R. Zhong. Analysis of stratum grouting influence on shaft lining stress with the methods of simulation and in site measurements[J].Procedia Earth and Planetary Science,2009(1) :497-502.

[3]廖雄华，周健，徐建平，等．粘性土室内平面应变试验的颗粒流模拟[J]．水利学报，2002,33(12)：11-16．

[4]蒋应军，任皎龙，徐寅善．级配碎石力学性能的颗粒流数值模拟方法[J]．同济大学学报(自然科学版)，2011，39(5)：699-704．

[5]CUNDALLPE，HARTRG. Numerical modeling of discontinue[J]. Engineering Computations，1992，9(2):101-113.

[6]周健，池永．砂土力学性质的细观模拟[J]．岩土力学，2003，24(6)：901-906．

[7]周健，张刚，孔戈．渗流的颗粒流细观模拟[J]．水利学报，2006，37(1)：28-32．

[8]吴顺川，金爱兵，高永涛．袖阀管注浆技术改性土体研究及效果评价[J]．岩土力学，2007，28(7)：1353-1359．

[9]孙锋，张顶立，陈铁林，等．土体劈裂注浆过程的细观模拟研究[J]．岩土工程学报，2010，32(3)：474-480．

[10]袁敬强，陈卫忠，谭贤君，等．软弱地层注浆的细观力学模拟研究[J]．岩土力学，2011，32(增2)：653-659．

[11]周健，池永，池毓蔚，等．颗粒流方法及PFC2D程序[J]．岩土力学，2000，21(3)：271-274．

[12]Itasca Consulting Group. PFC2D user’s manual (version3.1)[M]. Minneapolis， Minnesota: Itasca Consulting Group，Inc，2004.

[13] Itasca Consulting Group Inc.. PFC2D(particle flow code in 2D) theory and background[R]. Minnesota，USA：Itasca Consulting Group Inc.，2008.

[14]余华中，阮怀宁，褚卫江．岩石节理剪切力学行为的颗粒流数值模拟[J]．岩石力学与工程学报，2013,32(7)：1482-1490．

[15]徐芝纶．弹性力学简明教程[M]．北京：高等教育出版社，2005．

[16]曾胜，赵健，邹金锋．压密注浆极限注浆压力研究[J]．哈尔滨工业大学学报，2008，40(7)：1173-1176．

[17]王广国，杜明芳，苗兴城．压密注浆机理研究及效果检验[J]．岩石力学与工程学报，2000，19(5)：670-673．

[18]岩土注浆理论与工程实例协作组．岩土注浆理论与工程实例[M]．北京：科学出版社，2001．

Micromechanics particle flow numerical simulation research on soil grouting

QIN Pengfei

(School of Architectural Engineering,Zhengzhou University of Industrial Technology,Zhengzhou 450010,China)

Based on the principle of fluid-structure coupling numerical simulation program, PFC2D particles flow, which uses its built-in FISHTANK function library and FISH language, and the flow equation and pressure equation of fluid domain has been defined, the process of grouting slurry diffusion in the formation and shape are simulated and calculated. By adjusting the parameter of step and perm in PFC’s command stream, grouting effects in different penetration gravels were obtained. Numerical simulation indicates that action modes between serous fluid and ground soil are mutually affected by the grouting pressure, foundation structure will be destroyed as the pressure increase excessively.Stressed states around the drilling hole have been analyzed, its results comply with the simulation. When split grouting method occurs, porosity and strain increase. Conductivity of the slurry affects the grouting little in high-pressure grouting.

sandy soil;grouting;particle flow;numerical simulation; penetration

2016-05-16;

2016-06-12

国家自然科学基金(No.51279217)

秦鹏飞(1984- )，男，河南鲁山人，博士，副教授，主要从事地基处理方面的研究.E-mail:qinpengfei@emails.bjut.edu.cn

TU41

A

1671-9476(2016)05-0065-06

10.13450/j.cnki.jzknu.2016.05.017